在役高樁碼頭橫梁剩余壽命預測

孟靜，李鑫

（1.交通部天津水運工程科學研究所，水工構造物檢測、診斷與加固技術交通行業重點實驗室，天津300456；2.天津港工程監理咨詢有限公司，天津 300456）

天津港是國內最大的人工港，也是世界等級最高的人工深水港，是在淤泥質淺灘上人工挖海建港、吹填造陸建成的。因此，天津港的碼頭形式均以高樁碼頭為主，特別是高樁梁板式結構的應用最為廣泛。但因為此種結構形式的高樁碼頭在耐久性和對超載及裝卸工藝方面的適應能力較差，所以導致構件易損壞且難修復，故對其進行可靠度計算顯得尤為重要。

1 工程概況

天津港某港區高樁碼頭為連續梁板式承臺結構，由面板﹑面層、橫梁﹑門機梁﹑火車梁﹑樁﹑靠船構件等部分組成。構件均為預制安裝，接縫混凝土及面層為現澆，形成連續結構。由北到南共75個排架，排架間距7m，分為9個結構段，1～34排為雜貨泊位，34～75排為糧食泊位。該碼頭面頂高程為5.8m，前沿水深為-9m，碼頭分為前樁臺、后樁臺和接岸結構3部分，橫斷面見圖1。碼頭橫梁為混凝土梁，分2次澆筑，面板以下部分為預制混凝土T形梁，與面板連接部分為橫梁的現澆疊合部分，橫梁斷面圖見圖2，結構斷面特性見表1。采用C35混凝土，水灰比0.43，主筋保護層厚度60mm；底部配10φ20的II級縱向受拉鋼筋，上部配2φ14@250的水平分布筋，10φ14的短筋，豎向分布筋4φ14@250。裂縫寬度W=0.15mm，裂縫間距為180mm。

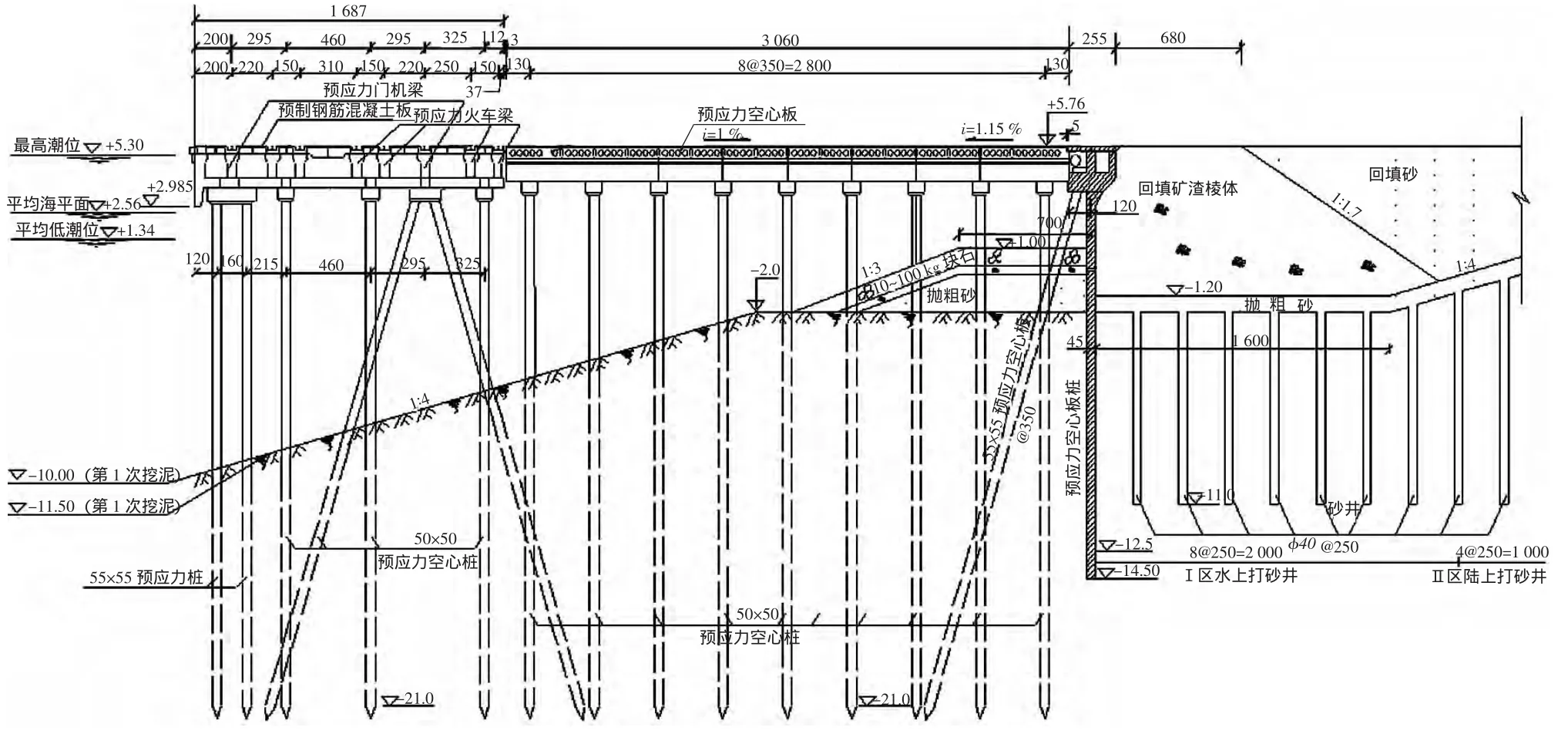
圖1 天津港某高樁碼頭橫斷面圖Fig.1 Cross-sectional view of a high-pile wharf of Tianjin Port

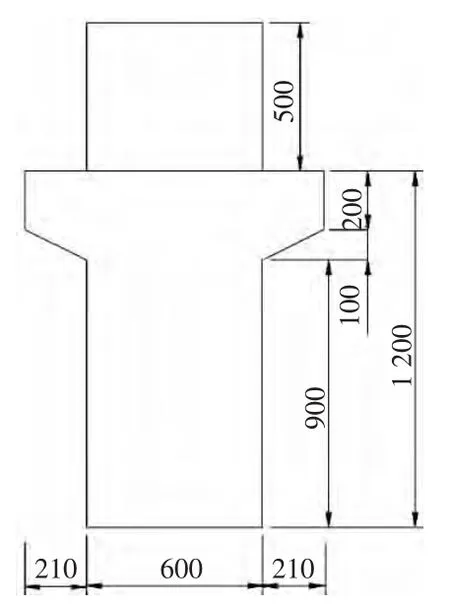
圖2 橫梁斷面圖（單位：mm）Fig.2 Beam cross section （mm）

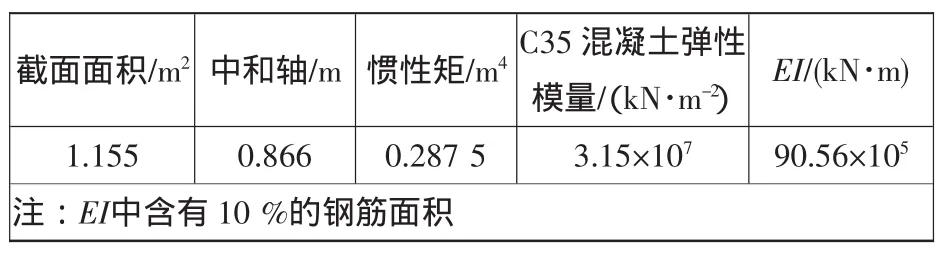
表1 橫梁結構斷面特性表Table 1 Beam cross-section characteristics

通過統計2009年該碼頭檢測評估過程中的實測數據，并由式（1）～（5），得出橫梁的鋼筋混凝土的統計參數見表2。

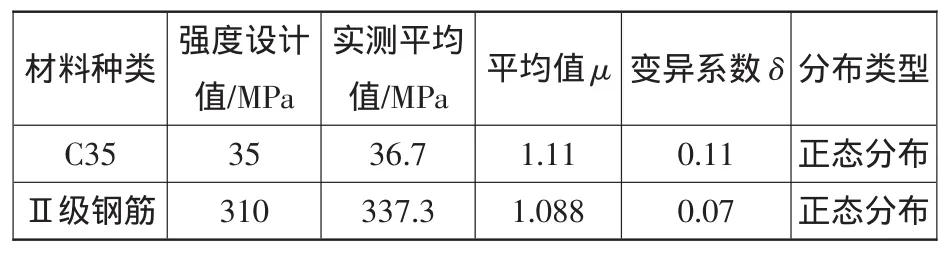
表2 碼頭橫梁鋼筋混凝土材料的統計參數Table2 Statistical parameters of beam reinforced concrete

材料強度的不定型Kf是結構中材料的實際強度fs與材料的強度設計值fk的差異，即：

式中：f為結構構件中材料性能值；fs為試件材料性能值；fk為規范規定的材料性能標準值；w0為反映結構構件材料性能與試件材料性能差別的影響系數，w0=1；K0為反映結構構件材料性能與試件材料性能差別的隨機變量；K1為反映試件材料性能不定性的隨機變量。

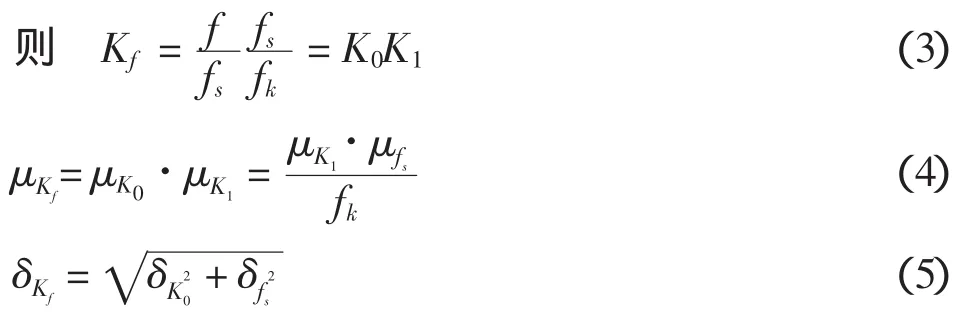
2 高樁碼頭橫梁可靠度計算

由于高樁碼頭抗力的影響因素比較復雜，本文擬采用時變動態可靠度的計算方法，計算碼頭橫梁結構承載力達到極限的時間：結構的時變動態可靠度（或可靠指標）可看作是結構服役時間的函數，給定其目標可靠度或目標可靠度指標β*后，則可由β*與動態可靠度指標β（t）的函數聯合求解，二者曲線交點對應的橫坐標，即為年數，此時間點為結構的使用壽命。

按照GB 50158—2010《港口工程結構可靠度設計統一標準》的規定，港口工程結構的目標可靠指標β*應根據結構的破壞類型和安全等級按表3 確定[1]。

表3 結構可靠度目標Table3 Goals of structural reliability

2.1 橫梁構件承載力極限方程

按照JTJ267—98《港口工程混凝土結構設計規范》[2]，本文采用鋼筋混凝土構件的正截面抗彎承載力計算模型，由受力平衡條件得：

式中：fc為混凝土軸心抗壓強度設計值，MPa；As，分別為銹后縱向受拉，受壓鋼筋的截面面積，mm2；fy，分別為銹前縱向受拉鋼筋抗拉、受壓強度設計值，MPa；b為矩形截面的寬度或T形截面的腹板寬度，mm；為受壓區鋼筋合力點至受壓邊緣的距離，mm；ky為銹蝕鋼筋屈服強度降低系數；ks為鋼筋與混凝土之間的協同工作系數。依據設計圖，根據受力分析選取該橫梁的最不利截面，結合式（6）～（7），得到該處抗彎極限承載力方程為：

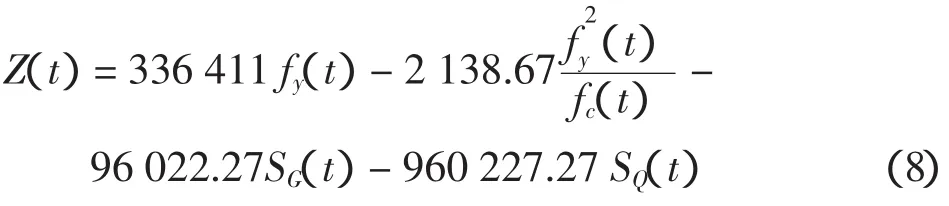
式中：fc（t）為隨時間變化的混凝土軸心抗壓強度值，MPa；fy（t）為隨時間變化的銹前縱向受拉鋼筋抗拉設計值，MPa；SG（t）為隨時間變化的結構永久荷載作用效應組合值，MPa；SQ（t）為隨時間變化的結構可變荷載作用效應組合值，MPa。

2.2 橫梁構件鋼筋混凝土銹蝕時間

由于混凝土中的氯離子擴散具有地域性這一特征，因此，在研究該港區氯離子時，選取了幾個典型的碼頭結構段作為研究對象，根據JTJ 302—2006《港口水工建筑物檢測與評估技術規范》對“鋼筋劣化耐久性專項檢測”中規定[3]：用沖擊鉆在結構混凝土尚未開裂、剝落的典型部位鉆取試樣，取樣是在垂直于梁側向表面的部位鉆取混凝土粉末，每鉆入1 cm深度所取得的混凝土粉末作為1個試樣，在每個取樣點鉆入深度為5 cm，每個測點共取5個試樣。將現場采集的待檢混凝土粉末配制成檢測溶液，利用混凝土快速氯離子檢測儀檢測溶液的氯離子含量，此含量即為結構中氯離子含量。檢測前應對儀器進行標定，檢測中依次對檢測液進行分別檢測，最終將測得結果和標定曲線進行對比。將結果帶入了菲克第二定律進行計算，可得出氯離子表面濃度以及擴散系數，見表4。

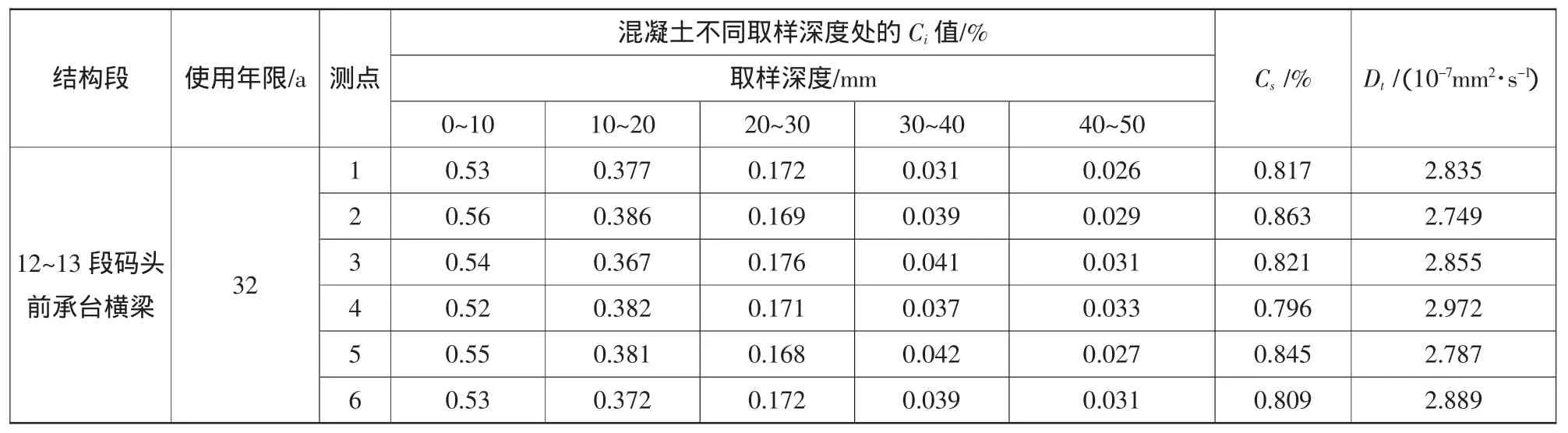
表4 天津港碼頭橫梁氯離子實測值Table 4 Chloride ion measured values of beams in Tianjin Port

按照JTJ302—2006《港口水工建筑物檢測與評估技術規范》中的規定，將上述實測數據帶入到菲克第二定律中進行計算[3]，即：

式中：Cx，t為齡期t時不同深度處的氯離子含量（以占膠凝材料質量百分率計）；Ci為混凝土中原始氯離子含量（以占膠凝材料質量百分率計）；Cs為混凝土表面氯離子含量（以占膠凝材料質量百分率計）；x為距離混凝土表面的深度，mm；Dt為氯離子擴散系數，mm2/s；t為混凝土暴露于環境中經過的時間，s。

由實測數據算出該處構件氯離子表面濃度Cs為0.825%（按與混凝土重量的百分比計算），擴散系數Dt為76.8mm2/a，代入下式[4-5]：

式中：Kc為混凝土總修正系數；Kce為水泥品種修正系數；Kel為地區影響系數；Kei為環境影響系數；Kt為混凝土養護系數，取值見表5；c為混凝土保護層厚度，mm；xc為混凝土碳化殘量，mm。

表5 計算參數表Table 5 Calculation parameters

根據《港口水工建筑物檢測與評估技術規范》計算得出該段碼頭的鋼筋開始銹蝕的時間=36.7 a，計算出混凝土碳化開始的時間為=75.9 a，則臨界時間為二者的最小值，則tp=36.7 a。

另外，根據鋼筋銹蝕量得出的平衡方程[6]計算出混凝土的開裂時間tcr=33.11 a，因此該碼頭在此時，即運行至32 a時，還不用考慮鋼筋銹蝕對其抗力的影響，但在tcr=33.11 a之后，就要將此影響考慮進去，為了更好地反映橫梁可靠度指標在服役基準期及以后的變化，本文選取了80 a為計算年限來計算該碼頭的可靠指標。

2.3 橫梁可靠度計算

根據上述分析，計算該碼頭橫梁結構的時變動態可靠度，擬以規范規定的50 a為基準期，每5 a為一個生命步長，一直計算到80 a，然后用Matlab軟件編制JC法程序[7]，計算出各個生命步長的可靠度指標β，并繪制動態可靠度曲線，見圖3，圖中橫線為臨界可靠度指標β=3.5。

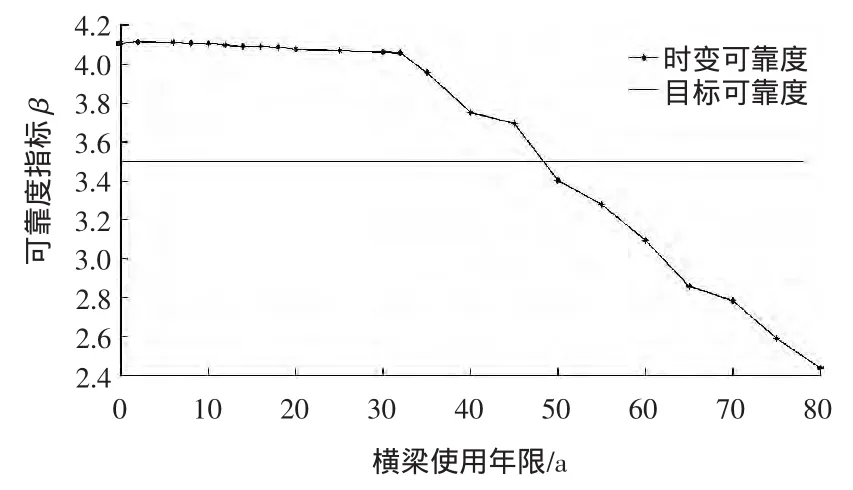
圖3 橫梁可靠度指標與使用年限的關系Fig.3 Relationship between the reliability index and service life of beam s

3 結果分析

首先，由計算可以看出：該碼頭在基準期內的可靠指標滿足規范規定值，由該計算得出其計算年限為48.3 a，與僅用氯離子侵蝕計算的使用年限為46.3 a基本相符合。其次，從計算可以看出，在結合混凝土開裂，鋼筋發生銹蝕以后，該橫梁可靠度指標下降較快，所以要預防發生鋼筋銹蝕，且一旦發生銹蝕現象，要及時進行維修。其次，在此次研究中發現高樁碼頭的橫梁損傷多是發生彎矩破壞，即其可靠指標是由構件的延性破壞所控制的，這是由于梁板式高樁碼頭構件截面設計較大，且跨度較大導致的，建議從設計方案上優化，合理改變橫梁的截面尺寸，最大程度使其彎、剪可靠度指標達到一致，從而使結構在服役期內滿足經濟合理，使用安全的需要。

[1] GB 50158—2010，港口工程結構可靠度設計統一標準[S].GB 50158—2010，Code for design of steel structure in port engineering[S].

[2] 黃長虹.在役高樁碼頭耐久性評估方法研究[D].天津：天津大學，2003.HUANG Chang-hong.Research on evaluation method of the durability of high-pile wharf in service life[D].Tianjin:Tianjin Univer-sity，2003.

[3] JTJ302—2006，港口水工建筑物檢測與評估技術規范[S].JTJ 302—2006，Technical specification for detection and assessment of harbour and marine structures[S].

[4] 王有志.橋梁的可靠性評估與加固[M].北京：中國水利水電出版社，2008：10-195.WANG You-zhi.Reliability evaluation and reinforcement of bridges[M].Beijing:China Water Power Press，2008：10-195.

[5] SONG Yu-pu，SONG Li-yuan，ZHAO Guo-fan.Factors affecting corrosion and approaches for improving durability of ocean reinforced concrete structures[J].Ocean Engineering，2004，31（5/6）：779-789.

[6] 牛荻濤，王慶霖，王林科.銹蝕開裂前混凝土中鋼筋銹蝕量的預測模型[J].工業建筑，1996，26（4）：8-13.NIU Di-tao，WANG Qing-lin，WANG Lin-ke.Predeterminate model of steel corrosion extent in reinforced concrete structures before producing corrosion crack[J].Industrial Construction，1996，26（4）:8-13.

[7] 張明.結構可靠度方法分析——方法與程序[M].北京：科學出版社，2009.ZHANG Ming.Structural reliability analysis-method and procedure[M].Beijing:Science Press，2009.