墩柱梁板式碼頭結構在三峽庫區的破壞分析

葉晨茂，王多銀，2，汪霏

（1.重慶交通大學河海學院，重慶 400074；2.重慶市航運中心，重慶 400074；3.重慶建筑工程職業學院，重慶 400072）

三峽成庫后，水深加大，險灘消失，內河碼頭的通航條件得到了極大的改善。為了適應庫區新的水文條件，同時為了打破內河碼頭利用枯水期施工的束縛，提出了針對庫區回水變動段的“大樁柱、大跨度”的碼頭結構形式[1]。該碼頭結構雖然曾有不少研究，但是針對這種“大樁柱、大跨度”碼頭的破壞研究甚少。本文以成庫后新建的重慶市主城港區納溪溝碼頭為依托，對該結構中的靠船墩進行數值模擬分析，預測靠船墩結構的開裂荷載和水平極限承載能力值，以及在最不利荷載工況作用下，結構的破壞形式及裂縫在碼頭結構當中的發展過程。

1 碼頭概況

重慶市納溪溝碼頭位于長江寸灘水文站下游5.5 km河道右岸，建設4個3000噸級泊位，1號、2號泊位采用分級直立式下河公路形式，3號、4號泊位采用直立岸壁、單跨橋吊墩式結構，占用岸線610m。該碼頭平臺長度233.4m，寬度41.75m，水工建筑物采用墩柱框架碼頭結構形式，碼頭平臺前沿由6個靠船墩（兼系船）及16個直徑為3m的圓形支撐墩組成，平臺中間采用22個直徑3m的圓形支撐墩，后方則由6個矩形支撐墩（4個長×寬=4.4m×3.2m，2個長×寬=6.0m×3.2m）和16個圓形支撐墩組成。2號和5號靠船墩（靠船墩1），承臺的大小：長×寬×高=9.8m×8.6m×3m，其下面的樁基是由2根φ1800mm和3根φ1500mm的鋼筋混凝土嵌巖鉆孔樁組成，后方矩形支撐墩下面的樁基則是采用5根φ1200mm的鋼筋混凝土嵌巖鉆孔樁構成；其余靠船墩（靠船墩2）前方承臺的大小：長×寬×高=9.6m×6.9m×3m，其下面的樁基則是采用5根φ1500mm的鋼筋混凝土嵌巖鉆孔樁，后方矩形支撐墩下面的樁基則是由4根φ1200 mm的鋼筋混凝土嵌巖鉆孔樁構成[2]。靠船墩的設置有利于提高碼頭的排架間距，且在船舶的靠泊過程中，船舶荷載主要作用在靠船墩上，在保護了大樁柱的同時也避免了直接承受船舶的撞擊。由于該結構形式的碼頭研究不多，因此，有必要針對該結構的破壞模式展開研究與分析。

2 有限元模型的建立

對于這種靠船墩形式的碼頭結構，不能再采用以往針對已建的架空直立式碼頭結構中廣泛采用的桿件系統進行模擬分析。根據其受力特性，采用實體結構與梁單元相結合的方法來模擬該碼頭結構。對于靠船墩、后方支撐墩以及承臺結構采用3D實體單元（Solid65單元），橫梁、橫撐、人字撐以及樁采用3D梁單元（BEAM189單元）。當不同種類單元的自由度相同時，采用共用節點即可；而當不同種類單元的自由度不同時，則需要建立“約束方程”[3]。在ANSYS中，其特有的BEAM189梁單元為三節點等參單元，每個節點具有 6 個自由度：Ux，Uy，Uz，ROTx，ROTy，ROTz；而其特有的SOLID65單元為八節點等參單元，每個節點具有3個自由度：Ux，Uy，Uz。所以，3D梁單元與3D實體單元在連接時，共用節點使其連接為鉸接，若要剛性連接可通過建立約束方程、設置剛性區、MPC184剛性梁等方法實現。在該碼頭結構的模型建立當中，采用的是自動建立約束方程來模擬兩種單元剛接處。樁的計算長度根據嵌固點法確定，樁端約束所有自由度。由于兩種靠船墩的結構形式類似，故本文僅對2號（5號）靠船墩進行數值模擬分析，其有限元模型如圖1所示。

圖1 靠船墩有限元模型Fig.1 Finite element model of dolphin

3 荷載工況組合

3.1 碼頭結構作用的恒載

1）靠船墩、支撐墩、承臺、橫梁、樁、橫撐、人字撐等構件的自重可在ANSYS中設置參數后自動施加（取g=9.8 m/s2），密度ρ=2500 kg/m3。

2）面板傳給橫梁的自重，面板按簡支板計算，直接作用在橫梁上的均布荷載：q1=0.5×11×25=137.5 kN/m。

3）前后邊梁、普通縱梁、軌道梁、鋼質軌道自重以集中力施加于其所在位置節點上，其值分別為：

前后邊縱梁：P1=1.32×11×25=363 kN（橫梁前段，11m長計，S=1.32m）；

軌道梁：P2=3.66×11×25=1006.5 kN（11m長計，S=3.66m）；

普通縱梁：P3=2.16×11×25=594 kN（11m長計，S=2.16m）；

鋼質軌道自重：P4=5 kN。

3.2 可變作用產生的作用效應

1）集裝箱裝卸橋（岸吊）

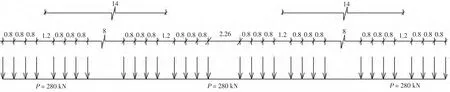
圖2 集裝箱裝卸橋計算圖Fig.2 Calculating chart of Container Bridge

集裝箱裝卸橋產生的作用由軌道梁傳給橫梁，軌道梁按簡支梁計算（圖2），其反力為：

前軌V1=2148 kN；后軌V2=2148 kN。

V1=V2=2P[11×8-（6.4+5.5+4.6+3.7+2.7+1.8+0.9）]/Ln=2148 kN

式中：P為最大輪壓，250 kN；Ln為計算跨徑，11 m。

2）水平力荷載

對于水平作用力，本文主要考慮的是水平撞擊力的作用。因此，根據作用在靠船墩不同層的系船梁的位置分9種工況，如圖3所示，撞擊力取值為1030 kN。

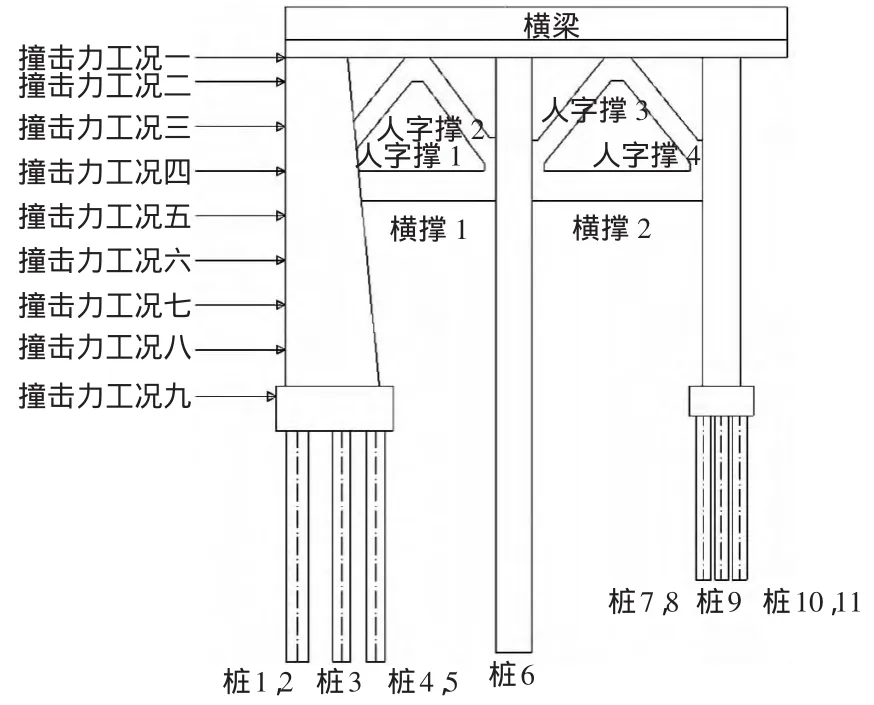
圖3 靠船墩撞擊力計算工況Fig.3 Calculated work condition of dolphin impact

3）堆荷

堆荷為30 kN/m2，經由面板傳遞給橫梁，其計算值為：q2=11×30=330 kN/m。

4 非線性分析中的計算設置

對于靠船墩鋼筋混凝土結構采用Solid65單元進行模擬。Solid65單元破壞面采用改進的William-Warnke五參數破壞曲面，對于材料的計算設置當中，采用Mises屈服準則和多線性等向強化模型（MISO）。

對于混凝土的應力-應變關系采用 Mander等[4-5]建議的本構關系進行計算：

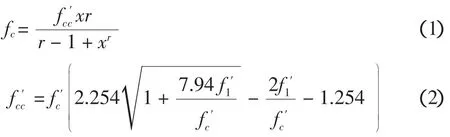
混凝土開裂準則為Rankine準則，當達到材料的最大拉應力時，混凝土發生開裂，拉應力的松弛系數考慮0.6；混凝土發生開裂后，當應變軟化到開裂應變的6倍后，應力為0[6]。開裂后，混凝土的閉合裂縫和張開裂縫剪力傳遞系數分別為0.5和 0.95。

5 計算結果分析

5.1 水平撞擊力作用下荷載位移曲線

按照碼頭結構的撞擊位置，將撞擊力分為9種分析工況（如圖4所示），以碼頭平臺面前沿線的角點為位移觀測點。計算得到有限元計算的荷載-位移曲線見圖4。

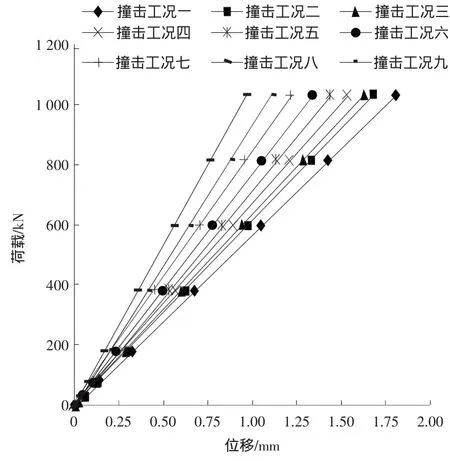
圖4 靠船墩荷載-位移曲線Fig.4 The load-displacement curve of dolphin

從圖4中可以得到以下結果：

1）當荷載作用在高水位時（即撞擊工況一），結構位移值最大，當結構作用在低水位時（即撞擊工況九），此時位移最小。在大小相同的撞擊力作用下，當撞擊力作用的位置越高，其位移越大。因此，撞擊工況一為9種撞擊工況當中的最不利的荷載工況。

2）從圖4可以看到，靠船墩結構的荷載-位移曲線成線性關系，表示在撞擊力（F=1030 kN）的作用下，結構當中的各個構件處于彈性階段內。

5.2 位移加載工況下荷載位移曲線

在撞擊力作用時，碼頭各個構件為彈性應力狀態，為了更加清楚地了解靠船墩結構在水平力作用下的破壞過程，采用在水平撞擊力處施加位移荷載，得到了等位移荷載作用下的極限承載力值。圖5為靠船墩結構的位移曲線圖。

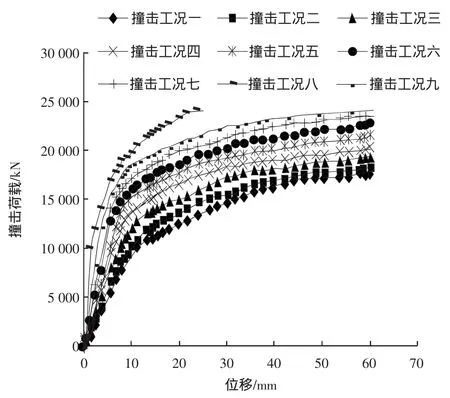
圖5 靠船墩在位移控制作用下荷載-位移曲線Fig.5 The load-displacement curve of dolphin under the effect of displacement control

從圖5中可以觀察到：

1）隨著撞擊高度的增大，靠船墩結構的極限承載能力值逐漸減小。對該結構而言，當撞擊高度在結構的最高層時（即為撞擊工況一），為其最不利撞擊工況。

2）對同一個靠船墩結構而言，隨著高度的變化，每一種撞擊工況之間的極限承載能力值的大小變化幅度在10%以內。表明該結構的整體剛度好，整體穩定性高。

5.3 最不利撞擊工況下的破壞模擬

1）靠船墩結構在最不利撞擊作用下的計算結果

由上一節的計算中得到，撞擊工況一的水平極限承載力最小，為9種工況當中最不利荷載工況。其荷載位移曲線見圖6。

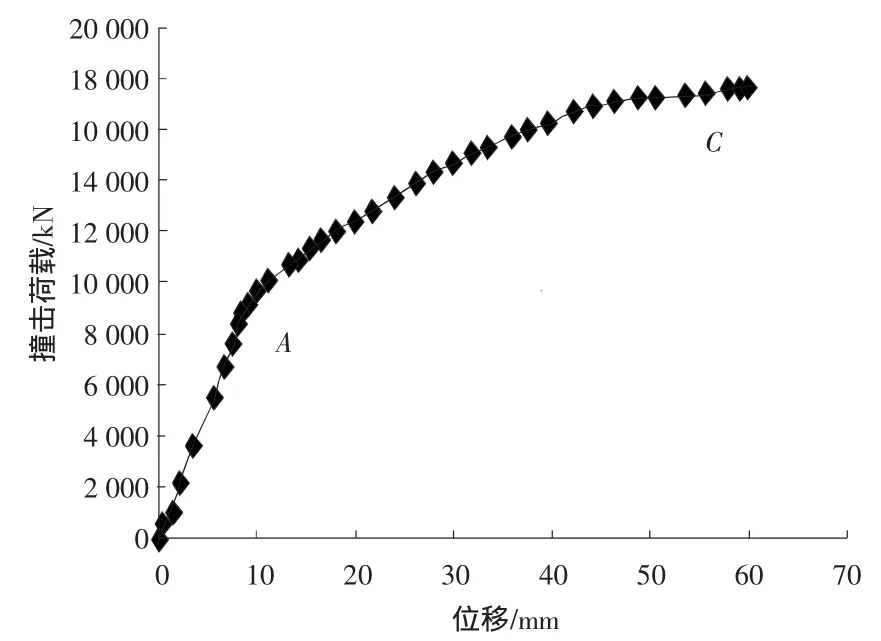
圖6 靠船墩在最不利荷載工況下荷載-位移曲線Fig.6 The load-displacement curve of dolphin under the most unfavorable load condition

從結構的荷載-位移曲線中可以清楚地看到，結構的整體變形過程可以分為3個階段：彈性階段—彈塑性階段—塑性階段。其中，從原點到A點為彈性應力階段，當荷載的大小值達到了A點時，靠船墩結構當中出現了第一條裂縫，當超過A點以后，結構進入了彈塑性階段，結構仍然能夠承受外荷載，直至達到結構的極限荷載值C點。在圖6中由有限元計算所得到的荷載-位移曲線沒有下降段，這是因為在有限元的計算設置當中，混凝土的本構關系所采用的是約束混凝土的本構關系，因此，所得到的曲線當中并沒有下降段。

2）靠船墩結構破壞形態的模擬

在有限元的計算過程中，為了得到收斂的計算結果，在計算設置中關閉了混凝土的壓碎選項，在靠船墩結構的破壞圖中僅僅以開裂體現，在ANSYS有限元軟件當中，采用的是紅、綠、藍3種顏色的小圓圈表示混凝土單元積分點處的3個開裂面。利用有限元軟件得到靠船墩結構在不同的受力階段下的破壞形態及發展過程，其在最不利撞擊工況下的應力云圖和最終破壞如圖7、圖8所示。

圖7 靠船墩最不利撞擊工況下的應力云圖Fig.7 The stress nephogram of dolphin under the most unfavorable impact condition

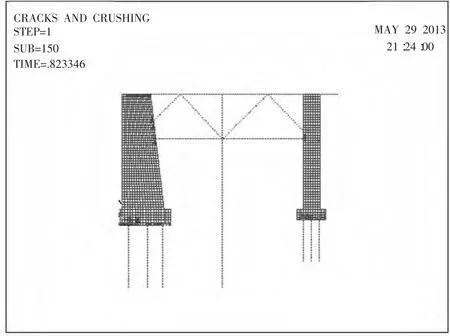
圖8 靠船墩最終破壞圖Fig.8 The ultimately damage of dolphin

對于靠船墩結構而言，結構中最先發生開裂的部位為靠船墩墩身底部與樁相互連接的部位，橫撐與人字撐同樣也是結構中容易開裂的構件，在工程設計中可考慮加大構件斷面尺寸，裂縫在靠船墩結構中發展的趨勢大致為：靠船墩承臺底部與樁相互連接部位；隨著荷載增加，裂縫在靠船墩承臺當中沿承臺的寬度、高度方向發展，同時，橫撐和人字撐的端部產生裂縫；到了破壞末期，靠船墩承臺高度方向裂縫幾乎布滿，后方支撐墩承臺中的裂縫雜亂無章，該區域混凝土被壓碎。

6 結語

本章利用復合材料細觀力學理論所得到的彈性模量值，對碼頭結構中的靠船墩結構建立了有限元模型，對各個有限元模型進行了非線性分析，得到了靠船墩結構在水平荷載作用下的受力情況，描繪出了對應不同的撞擊位置的荷載-位移曲線，通過分析得到了其最不利荷載工況，著重分析了在最不利荷載工況下的破壞形態。主要得到以下幾點結論：

1）在撞擊力荷載（F=1030 kN）作用下，碼頭結構處于彈性應力階段，表明該碼頭結構具有足夠大的剛度。隨著撞擊荷載作用位置的增大，碼頭結構的位移變化越大，因靠船墩結構的剛度較大，其位移變化值偏小。

2）通過施加等位移荷載作用，得到了靠船墩結構的水平極限承載能力值。隨著撞擊高度的增加，結構的水平極限承載能力值減小，當撞擊力作用在靠船墩結構的最高層時，為結構的最不利撞擊工況。

3）在最不利荷載作用下，通過分析得到了靠船墩的破壞形態和裂縫的發展過程。

[1] 王多銀，楊洋，黃然，等.墩柱梁板式碼頭結構在三峽庫區的推廣應用[J].水運工程，2011（12）：91-94.WANG Duo-yin，YANG Yang，HUANG Ran，et al.Popularization and application of pier beam slab terminal structure in Three Gorges reservoir[J].Port&Waterway Engineering，2011（12）：91-94.

[2] 汪霏，王多銀.三峽庫區新型架空直立式碼頭結構模態分析[J].水運工程，2013（1）：81-84，113.WANG Fei，WANG Duo-yin.Modal analysis of new-style overhead vertical wharf in Three Gorges reservoir area[J].Port&Waterway Engineering，2013（1）:81-84，113.

[3] 王新敏.ANSYS工程結構數值分析[M].北京：人民交通出版社，2007.WANG Xin-min.ANSYS numerical analysis of engineering structures[M].Beijing:China Communications Press，2007.

[4] MANDER JB，PRIESTLEYM JN，PARK R.Theoretical stressstrain model for confined concrete[J].Journal of Structure Engineering，ASCE，1988，114（8）：1804-1826.

[5] MANDER JB，PRIESTLEYM JN，PARK R.Theoretical stressstrain behavior of confined concrete[J].Journal of Structure Engineering，ASCE，1988，114（8）：1827-1849.

[6] CHRISTIANA DYMIOTIS，ANDREAS J KAPPOS，MORIOS K CHRYSSANTHOPOULOS.Seismic reliability of RC frame with uncertain drift and member capacity[J].Journal of Structural Engineering ，1999，125（9）：1038-1047.