基于小波字典稀疏表示的SAR圖像目標識別?

田莉萍,王建國

(電子科技大學電子工程學院,四川成都611731)

0 引言

近年來稀疏表示理論得到了進一步的發展,尤其是2006年壓縮感知理論[1]的提出更推動了稀疏表示理論在各個領域的應用。文獻[2]首先將稀疏表示理論應用到人臉識別領域,識別效果良好,識別率均優于最近鄰法、線性SVM算法等。而對雷達目標電磁散射特性的研究結果表明,在高頻區雷達目標可用少數幾個散射中心描述。這種性質和稀疏分解的要求十分吻合,有利于圖像分析與目標識別[3]。文獻[4]將壓縮感知與SAR目標識別系統結合起來,驗證了該識別方法的有效性,并對于遮擋具有一定的魯棒性。文獻[5]提出基于特征構造冗余字典的方法,區別于傳統的基于像素的構造方法,使得冗余字典維數更低,提高了識別效率。

劉振等人提出的基于稀疏表示的SAR圖像目標識別方法(Sparse Representation based Classification,SRC)[6],直接在圖像域進行主元分析,提取2DPCA特征向量作為冗余字典的原子向量。而本文將原始圖像變換到小波域,建立小波域SAR圖像特征模型,得出小波低頻成分可充分表征目標類別信息的結論。提出將主元分析運用到二維離散小波變換所獲得的SAR圖像低頻信息上的方法,通過在此空間進行2DPCA特征抽取,理論上獲得了維數更低的特征向量。對比其他識別算法,本文算法無需對原始SAR圖像進行預處理,解決了針對不同SAR圖像預處理算法自適應性難以保證的問題,大大提高了算法通用性。最后,基于MSTAR數據庫的實驗結果顯示,由于結合了小波變換、2DPCA及SRC的優點,較單獨基于圖像域的SRC算法,本文算法識別速度更快、噪聲魯棒性更高。

1 稀疏表示理論簡介

記A i={a i,1,a i,2,a i,3,…,a i,ni}∈R m×ni為單個訓練樣本集,元素a i,j是m維的矢量,代表被標記的第i類目標中第j個訓練樣本對應的特征列向量。因此,總訓練樣本集由A={A1,A2,…,A k}∈Rm×n構成,此時稱集合A為冗余字典,元素a i,j為原子。對于任意測試樣本y∈R m×1,都可以表示成原子a i,j的線性疊加,x j記為稀疏分解系數:

鑒于字典A的冗余性,原子a i,j不再是線性獨立的,故方程組(1)的解是欠定的。為得到最稀疏的解,稀疏求解問題可以表示為

而求解包含?0范數的組合優化問題,是個NP-難題。但是,Donoho已經從理論上嚴格證明了在一定條件下?1范數和?0范數的求解結果是等價的[7],可以用代替。因此,式(2)的稀疏求解模型在包含噪聲的情況下更新為

2 小波域SAR圖像特征模型分析

稀疏表示的識別機理是,測試樣本能被同類訓練樣本構造的字典原子稀疏線性表示。測試樣本在稀疏分解后,對應目標類別的系數能量較大,即稀疏系數具有類內能量集中的特點。綜合電磁散射機理可知,確定性人造目標由一系列強散射點組成,其幅度能量主要集中在圖像的低頻穩定部分,而背景雜波、噪聲等干擾是隨機出現的,其幅度能量分散在整個頻帶中。引入二維離散小波分解技術,將有效表征目標信息的低頻信息分離出來。原始SAR圖像經小波分解后,低頻成分描述目標的整體能量信息,高頻成分描述背景雜波或噪聲信息。

由二維離散小波分解定義可知,小波分解系數包含四個部分。因此,經2DDWT變換后,小波域SAR圖像特征模型為

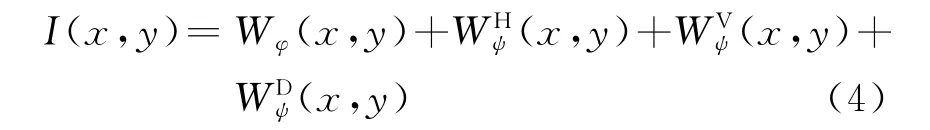
式中,Wφ表示低頻近似系數;WHψ,WVψ,WDψ分別表示水平、垂直和對角方向的高頻細節系數。圖1表示原始SAR圖像經一級小波分解后,獲得的不同頻段子圖像。

圖1 SAR圖像一級小波分解圖

圖2表示第一類測試樣本,分別在原始圖像、小波域中各分量構造的冗余字典下稀疏系數的分布。圖2(a)中原始SAR圖像的分解系數分布不集中,未表征類別信息不利于識別;圖2(b)中SAR圖像小波域低頻成分的分解系數具有類內能量集中的特點,類別信息明顯有利于稀疏表示識別;而圖2(c)、(d)、(e)中高頻成分的稀疏系數能量分散,屬于不利于稀疏表示識別的成分應去除。引入二維離散小波變換后,提取出對稀疏表示識別有利的低頻信息,去除干擾識別結果的高頻噪聲及背景雜波分量,在壓縮原子維數的同時提高了識別率。

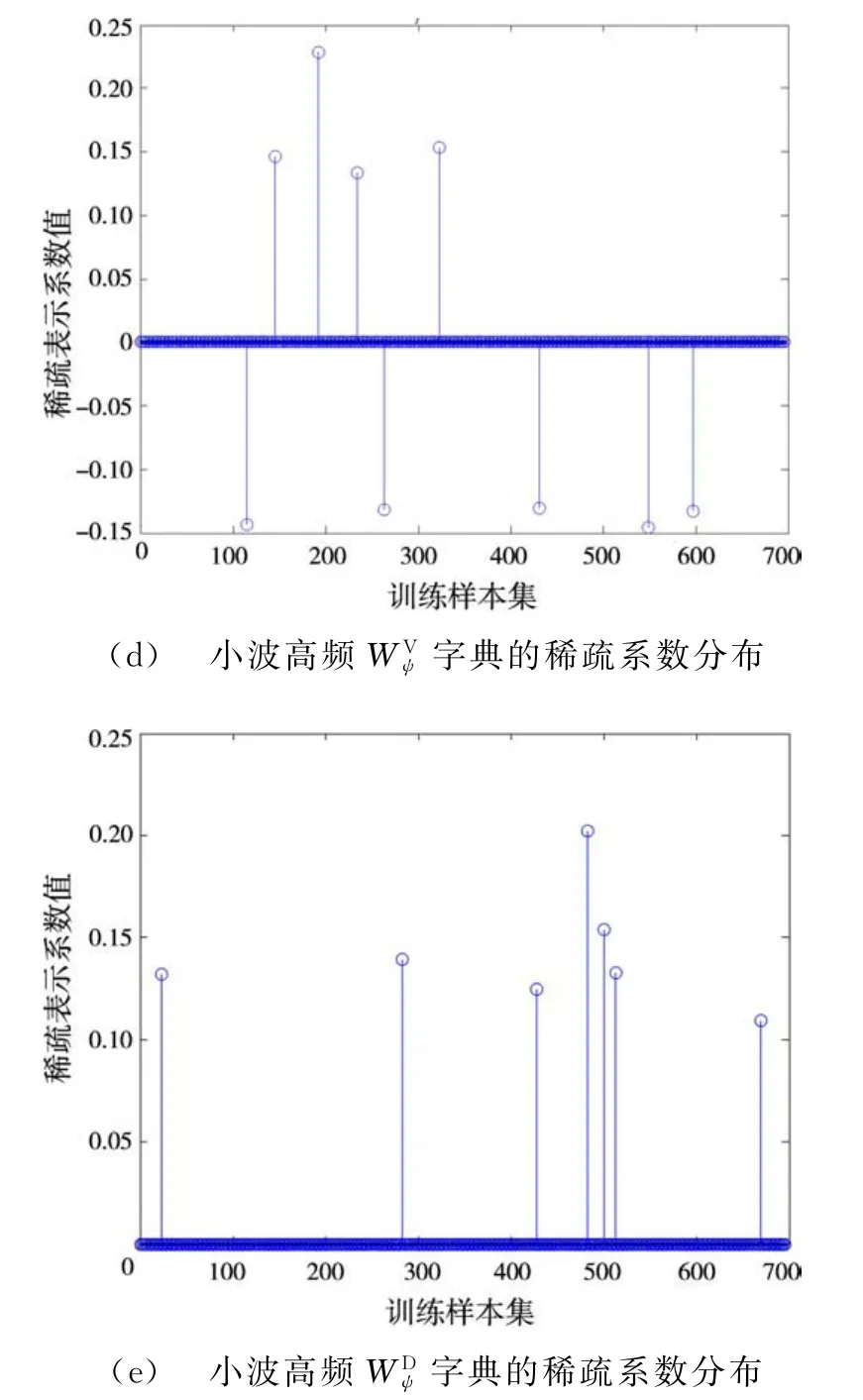
圖2 不同冗余字典下的稀疏分解結果

3 算法實現

根據SAR圖像小波低頻成分良好的稀疏表示能力,結合稀疏表示識別方法的基本思想,本文算法整體框圖如圖3所示。由圖3可知,算法核心問題為:(1)小波字典的構造;(2)快速有效的稀疏求解方法。下面將圍繞這兩個問題進行分析。

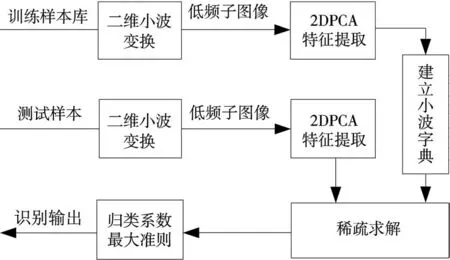
圖3 本文算法的整體框圖

3.1 小波字典的構造

在小波字典的構造中,首先利用小波分解提取SAR圖像訓練樣本的低頻子圖像,然后提取該子圖像的2DPCA特征向量作為字典原子保存。結合了小波分解與2DPCA方法的優點,由全部訓練樣本的特征向量構造小波字典,有效地降低了特征維數、提高了識別效率。此處不再贅述二維離散小波變換理論,下面為2DPCA特征向量的提取過程。

假設訓練樣本小波分解后,低頻子圖像集為{I1,…,I n},且I i∈R h×l,i=1,…,n,n為訓練樣本總數。首先將圖像進行中心化處理,即,其中為所有訓練樣本的均值圖像。訓練圖像的協方差矩陣D定義為

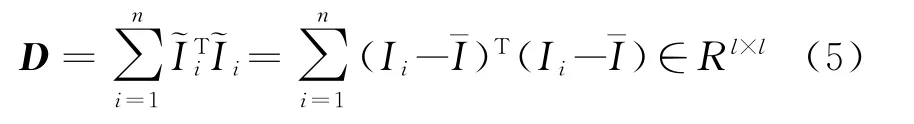
投影矩陣V可由D的前r個較大特征值λ1,…,λr對應的特征向量[v1,…,v r]組成[8]。因此,對于任意樣本圖像I i∈R h×l,其2DPCA特征F2DPCA=[f1,…,f r]=~I i[v1,…,v r]=(I i-I)V∈R h×r。

3.2 稀疏求解算法

正交匹配追蹤算法(OMP)作為對信號稀疏分解的算法之一,其應用最為廣泛,因為它在信號分解的稀疏性和計算復雜度之間作出了較好的折中和平衡[9]。OMP算法的流程與步驟如下:

算法流程

輸入:稀疏字典D={v1,v2,…,v N},測試樣本信號y,稀疏度K;

輸出:x的K-稀疏的逼近x。

算法步驟

(1)初始化:初始殘余量r0=y,索引集Λ=Φ,迭代次數t=1,且先驗稀疏度K已知;

(2)找出殘差r與字典D中的原子v i內積最大值所對應的腳標λ,即

(3)更新索引集:Λt=Λt-1∪{λt},由索引集得重建原子集合V t=[V t-1,vλt];

(5)更新殘余量:r t=y-V tx t,t=t+1;

(6)判斷是否滿足t＞K,若滿足,則停止迭代;若不滿足,則執行步驟(2)。

由算法的迭代終止條件可知,稀疏度值K實質決定了稀疏分解系數x t的非零解個數。故不同稀疏度的測試樣本稀疏求解后,所對應的稀疏系數非零解個數不等。由于實際中K未知需要估計,為避免估計每個測試樣本的稀疏度K,提出了一種稀疏度自適應的改進OMP算法。改進算法的關鍵是迭代終止條件的更改,用稀疏系數的類別統計量c k＞C替代t＞K作為終止條件,c k的定義是非零系數屬于第k類的個數。類別統計常量C代替稀疏度K,實驗驗證C取2～5時識別性能最佳,實驗中取C=3。改進后,不同測試樣本的分解迭代次數t不再由K決定,而是自適應的變化直到滿足某一類非零系數個數大于C,即實質上實現了稀疏度的自適應變化。改進O MP算法以類別信息量作為迭代終止條件,更加符合識別要求。

3.3 分類識別

設由改進O MP算法得到的稀疏分解系數為x,記x=(x1,1,…,x1,n1,…,x k,1,…,x k,nk)T,其中共有N類訓練樣本,第k類樣本總數為n k。而如何根據稀疏系數進行分類識別,也是SAR圖像稀疏表示識別的關鍵所在。本文采用歸類系數最大準則得到識別結果,歸類系數最大準則的定義是:分別記各類分解系數的2范數為歸類系數,將歸類系數最大值對應的訓練樣本所屬類別作為測試樣本的類別。歸類系數定義為

圖4為三類不同目標在特征冗余字典下的稀疏表示識別結果。由圖4可知,稀疏分解系數主要集中在一類上,由其歸類系數最大值對應類作為識別結果輸出。

圖4 三類目標的稀疏表示識別結果

4 實驗結果分析

實驗采用MSTAR SAR數據,它是迄今公開的較為完備地評價SAR ATR算法性能的標準數據。圖像數據的切片大小為128像素×128像素,分辨率為0.3 m×0.3 m,包括了俯仰角在17°和15°下的三類目標,分別可用作實驗的訓練樣本和測試樣本。選擇17°俯仰角下的三類目標數據作為訓練樣本,15°俯仰角下的目標數據作為測試樣本,表1列出了所用數據樣本的型號和個數。

表1 實驗樣本數據簡介

基于MSTAR SAR數據設計了三個識別實驗,實驗思路如下:(1)通過分析不同小波分解級數下識別性能的差別,確定出最佳小波分解級數;(2)確定最佳小波分解級數后,重點分析小波變換對于稀疏表示識別的影響,對比引入小波變換前后識別性能的差異;(3)驗證非理想情況下,本文算法對于噪聲的魯棒性。

4.1 實驗1

引入小波變換后,實驗分別驗證了小波基種類與小波分解級數對識別結果的影響。實驗顯示,小波基的選擇對于識別結果影響不大,而小波分解級數對識別性能有影響。實驗中選取‘db1’作為小波基,統計不同級小波分解對應的識別結果,得出在相同原子維數情況下識別性能最優的小波分解級數。由圖5的識別性能對比曲線可知,二級小波分解較一級、三級分解的識別性能更佳。因為,其識別率隨著原子維數增加呈上升趨勢,未出現異常值。當二級小波分解原子維數為480時達到100%的識別率,一級小波分解在原子維數為512時識別率為99.83%,三級小波分解最高原子維數為256,當其達到最高原子維數時識別率為98.63%。由于原子維數越少識別時間越短,綜合識別效果與效率,二級小波分解為最佳分解級數。

圖5 不同級小波分解下的識別性能對比曲線

4.2 實驗2

在二級小波分解級數的前提下,通過對比引入小波變換前后的識別率,結果表明引入小波變換可大大提升稀疏表示識別算法的性能。表2隨機簡單對比了以小波變換取代預處理后的識別結果,由表2可知引入小波變換后識別率獲得提高,且省去了繁瑣的預處理過程,因而識別時間大大減少。

表2 引入小波變換前后的識別結果對比

表2中各數據及方法說明:(1)其中原子維數為128×10,64×6的意義:10,6維代表由2DPCA所得的前10,6個特征向量作為特征原子,而128維、64維分別代表圖像字典和小波字典的原子維數大小;(2)方法1中的預處理定義參考文獻[6],具體過程如圖6所示。

統計不同原子維數下兩算法的識別結果,并畫出識別性能對比曲線如圖7所示。對比曲線表明,引入小波變換后識別性能大大提高,故加入小波變換是十分有效的。

4.3 實驗3

向原始樣本圖像添加椒鹽噪聲,噪聲密度比分別為0.02,0.04,0.06,0.08和0.10,圖8為不同噪聲程度下的各算法識別率結果。結果顯示本文算法對于椒鹽噪聲的魯棒性,較其他稀疏識別算法的識別結果更為穩定可靠。原因在于本文算法引入小波變換后,只提取小波低頻子圖像的2DPCA特征向量作為冗余字典原子,去掉了高頻噪聲的干擾,使得抗噪性能更好。

圖6 SAR圖像預處理流程

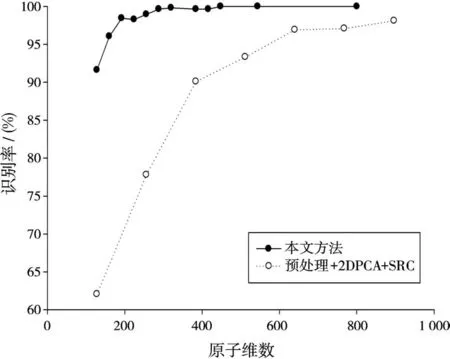
圖7 加入小波處理前后識別性能對比曲線

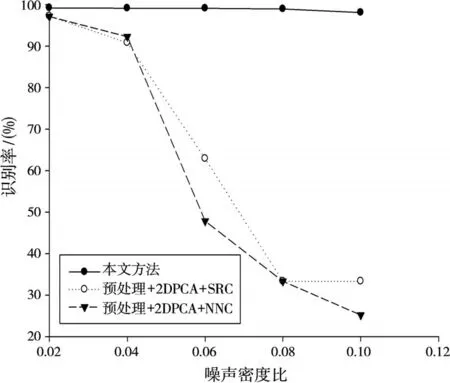
圖8 不同噪聲密度比下各算法識別率的對比曲線

5 結束語

本文針對現有稀疏表示識別算法基于圖像域構造冗余字典的不足,通過對比圖像域、小波域各成分稀疏表示能力的差異,得到小波低頻成分對識別更有利的結論,由此提出基于小波域主元分析的SAR圖像稀疏表示識別算法。這一算法的優越性在于擺脫了傳統SAR識別算法對于預處理過程的依賴性,結合了二維小波分解與二維主元分析的優點,使得基于稀疏表示的SAR圖像識別方法特征維數更少,識別效率更高。同時,只保留小波低頻子圖像,去除了高頻噪聲干擾,使得算法抗噪效果更好。通過MSTAR實測SAR圖像數據的實驗結果表明,本文算法的識別性能比基于圖像域的SRC算法更優。

其他濾波方法中,經高斯濾波與下采樣處理后,獲得的識別結果不及小波處理。原因在于本文算法成立的基礎,由第2小節小波域SAR圖像特征模型分析知,僅小波域的低頻成分對目標的稀疏表示能力好,僅由低頻成分所構成的小波字典對應的稀疏系數集中分布在第一類,與稀疏表示的理論相符。而其他類似于小波字典的冗余字典構成方法,后續研究過程有待繼續深入。

[1]Donoho D L.Compressed Sensing[J].IEEE Trans on Information Theory,2006,52(4):1289-1306.

[2]李偉紅,龔衛國,陳偉民,等.基于小波分析與KPCA的人臉識別方法[J].計算機應用,2005,25(10):2339-2341.

[3]鄭純丹,周代英.稀疏分解在雷達一維距離像中的應用[J].雷達科學與技術,2013,11(1):55-58.ZHENG Chun-dan,ZHOU Dai-ying.Research on High Rasolution Range Profile Based on Sparse Decomposition in Radar[J].Radar Science and Technology,2013,11(1):55-58.(in Chinese)

[4]高敏.基于CS的SAR目標識別[D].西安:西安電子科技大學,2010.

[5]王燕霞,張弓.基于特征參數稀疏表示的SAR圖像目標識別[J].重慶郵電大學學報(自然科學版),2012,24(3):308-313.

[6]劉振,姜暉,王粒賓.基于稀疏表示的SAR圖像目標識別方法[J].計算機工程與應用,2012,31(9):1-5.

[7]Chen S,Donoho D,Saunders M.Atomic Decomposition by Basis Pursuit[J].SIAM Journal on Scientific Computing,2001,20(1):33-61.

[8]胡利平,劉宏偉,尹奎英,等.基于G2DPCA的SAR目標特征提取與識別[J].宇航學報,2009,30(6):2322-2327.

[9]王燕霞,張弓.一種改進的用于稀疏表示的正交匹配追蹤算法[J].信息與電子工程,2012,10(5):579-583.