基于遺傳算法的組網雷達優化部署?

張 遠,方 青,曲成華

(中國電子科技集團公司第三十八研究所,安徽合肥230088)

0 引言

雷達組網預警探測系統通過融合不同體制、不同功能、不同頻段的多雷達情報,實現整體探測和情報共享,具有很強的反隱身、抗干擾、反低空/超低空突防、抗摧毀能力,極大地提高了現役雷達的作戰效能。雷達網功能的發揮,依賴于各組網雷達在空間和頻率上的分布關系,優化部署是實現雷達網作戰效能倍增的前提和基礎。目前雷達網優化部署研究主要集中于全局未知時的雷達網部署,采用的方法主要是枚舉法、專家推理法和遺傳算法等[1-3],枚舉法和專家推理方法存在組合爆炸和執行速度較慢等缺點,當組網雷達數較多時,幾乎不可能得到優化部署方案;另外這些方法均未考慮在實際雷達部署中的限制條件,部署結果的可用性不足。本文基于遺傳算法的雷達網優化部署方法結合GIS(地理信息系統)信息,在充分考慮雷達部署的各種限制條件基礎上,采用遺傳算法,通過一定數量的染色體群世代更迭,優勝劣汰,能較快地使部署接近最優(次優)解,避免了枚舉法的執行速度慢和專家推理法的組合爆炸問題。

1 基于遺傳算法的雷達組網優化部署原理

1.1 組網雷達優化部署的原則

組網雷達優化部署的目的是實現雷達網的無縫、連續覆蓋,通過多重覆蓋提高目標發現概率和目標更新數據率,因此組網雷達優化部署應該遵循連續性、嚴密性和重疊性的原則。

連續性:在雷達網探測區域內,目標的發現概率大于要求的門限值,目標能連續跟蹤。

嚴密性:部署完成后,要求的探測空域在各高度層上均能被完全覆蓋,不存在探測空洞和盲區。

重疊性:雷達網具備一定的重疊區域,達到雷達組網性能倍增的目的,實現雷達組網的功能。

為滿足上述部署原則,因此雷達配置必須滿足下列四個要求:

(1)高、中、低與遠、中、近距離探測一體化,保障雷達網威力覆蓋的連續性、嚴密性;

(2)警戒與保障引導一體化,保證雷達網警戒與保障的威力范圍;

(3)頻率與空間一體化,滿足系統整體抗干擾、反隱身的功能要求;

(4)機動、隱蔽與防護一體化,保障系統的機動、隱蔽、雷達接入和提高防護能力。

1.2 優化部署約束條件

雷達組網的優化部署是一個多約束條件的優化問題,即雷達部署必須滿足下列條件:

(1)雷達站位置相對固定,雷達只能部署在雷達站;

(2)雷達站地形、地貌條件,如雷達站可以部署的雷達數量;

(3)雷達站通信條件;

(4)雷達數量和種類相對固定,雷達種類和數量的選擇不能超過該范圍;

(5)雷達部署與配置的四個一體化要求。

在采用遺傳算法進行尋優時,將約束條件作為子代生成的前提,即在初始種群生成、交叉、變異等操作時,只能從合法(滿足約束條件)的父代中生成新的合法子代,將有約束條件的優化問題轉化為無約束的優化問題[4-7]。

1.3 優化部署的目標函數

組網雷達優化部署的目的是充分發揮多雷達在空間、頻率上的互補和倍增優勢,提高雷達網的整體探測性能,因此組網雷達優化部署應該達到的目的包括:在保證雷達網覆蓋連續性、嚴密性和重疊性的基礎上,提高隱身目標、小目標、低空目標、高速高機動目標的探測能力;提高目標的綜合抗電子干擾能力;提高目標定位跟蹤精度;在不浪費雷達資源的條件下,充分發揮雷達網的整體探測優勢,因此,組網雷達優化部署的目標函數可以定義為

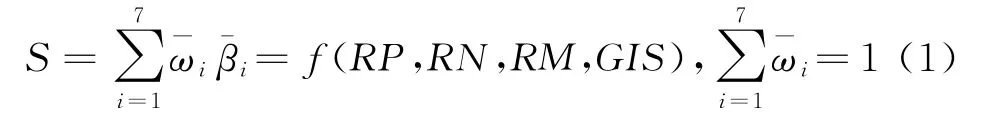
式中,RP為雷達部署位置;RN為部署雷達數量;RM為部署雷達型號;GIS為雷達陣地條件;為評價因子權系數(可根據雷達網主要作戰意圖改變);為相應的雷達網性能評價因子的歸一化值。雷達網性能評價因子包括:

(1)嚴密性評價因子β1

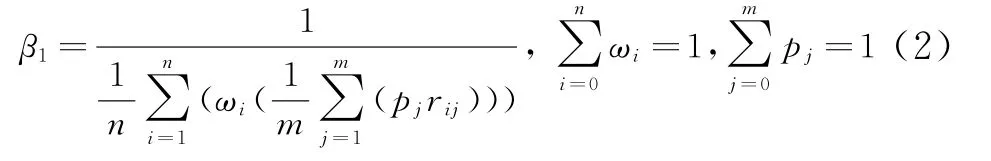
式中,n為高度采樣數;m為方位采樣數;ωi為高度層i的盲區等效半徑重要性系數;p j為高度層i中第j個方位的盲區等效半徑重要性系數;r ij為高度層i中第j個采樣方位的盲區等效半徑。嚴密性評價因子衡量雷達網覆蓋是否有盲區或空洞。

(2)連續性評價因子β2

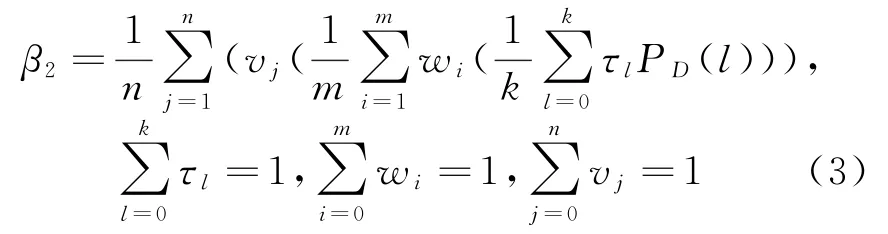
式中,k為距離采樣數;w i為高度層j中第i個采樣方位的發現概率重要性系數;τl為同一方位上的每個采樣點的發現概率重要性系數;P D(l)為每個采樣點對典型目標的發現概率。連續性因子衡量雷達網目標連續探測和跟蹤的范圍。

(3)重疊性評價因子β3

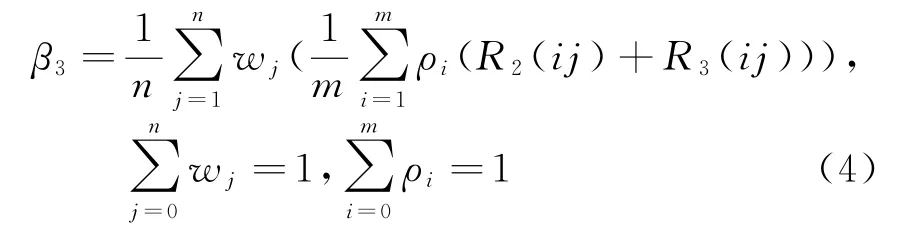
式中,w j為高度層j的重疊區域等效半徑重要性系數;ρi為高度層j中第i個方位的重疊區域等效半徑重要性系數;R2(ij),R3(ij)分別為高度層i中第j個采樣方位的二重、三重重疊區域的等效半徑。重疊性因子衡量雷達網重疊區域的大小。

(4)目標探測能力評價因子β4

式中,φk為低空目標、隱身目標、小目標和高速高機動目標探測能力的權系數;β4k分別為低空目標、隱身目標、小目標和高速高機動目標探測能力,定義為

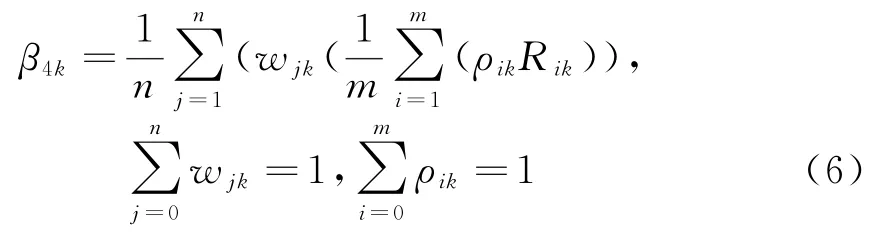
其中,w jk為高度層j的探測距離重要性系數;ρik為高度層j中第i個采樣方位的探測距離重要性系數;R ik為第i方位上對典型目標的探測距離。目標探測能力評價因子衡量雷達網對低空目標、隱身目標、小目標和高速高機動的探測能力。

(5)抗干擾能力評價因子β5

式中,ε=m/n為空域抗干擾能力因子;為頻域抗干擾能力評價因子,其中fmax為網中雷達的最高頻率,fmin為網中雷達的最低頻率,B0為實際雷達頻帶寬度,p為雷達網的頻率重疊系數。抗干擾能力評價因子通過空間和頻域抗干擾能力衡量雷達網的綜合抗電子干擾能力。

(6)探測精度評價因子β6

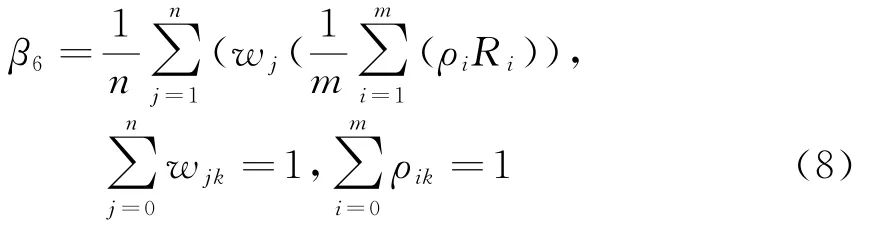
式中,w j為高度層j的探測距離重要性系數;ρi為高度層j中第i個采樣方位的探測距離重要性系數;R i為第i方位上探測圓精度小于500 m的最大距離。探測精度評價因子衡量雷達網目標定位的精度。

(7)資源使用率評價因子β7

資源使用率評價因子衡量雷達網資源使用,目的是在保證雷達網作戰效能的基礎上,盡量節省雷達資源。

2 基于遺傳算法的雷達組網優化部署算法結構

2.1 初始種群生成

在雷達組網中,雷達與陣地之間的組合關系是所求問題的信息,各雷達陣地采用符號編碼方法,m個陣地對應的編碼分別為(1,2,3,…,m),則n個雷達與m個陣地之間的組合關系如表1所示。

因此,每個雷達的陣地編號即為一個染色體編碼,n個雷達的部署就可以形成一個染色體串(P1,P2,…,P i,…,P n),其中

若雷達R i對應的雷達站編號P i為0,則表示該雷達不部署在任何陣地,一個染色體串形成一種部署方案。

隨機生成l個滿足約束條件要求的部署方案{A1,A2,…,A k,…,A l},其中A k=(P1k,P2k,…,P ik)[7-8],用這l種部署預案組成遺傳算法的初始種群。

各種群的適應度函數設計為式(1),直接采用優化部署的目標函數計算各種群適應度,衡量部署方案的優劣。

2.2 選擇

選擇是根據適者生存的原則選擇生成下一代個體(方案)的父本,以適應度為選擇原則,選擇出適應度大的部署方案直接傳給下一代,并淘汰劣質方案。

由適應度計算每種方案的被選擇概率,第i個部署方案被選擇參與下一代種群的概率為

為增加適應度高的個體被選擇的概率,采用輪盤賭式的正比選擇法,即產生一個取值范圍在0和之間的均勻分布的隨機數r,選擇滿足式(12)的第i個部署方案作為匹配集。

為保證遺傳算法的收斂性,保證最優個體不被破壞,能夠被復制到下一代,采用最優保存策略,即將適應度最高的個體替換下一代個體中適應度最差的個體,這樣適應度最高的個體能保存到下一代種群中。

2.3 交叉

采用一點交叉的方法進行交叉操作,在被選中用于繁殖下一代的個體中,以交叉概率pc生成一個“一點交叉”的交叉位,隨機不重復的從中間群體中選擇兩個個體,對交叉位以后的基因進行交叉運算,直到中間群體中所有的個體都被選擇過,交叉過程必須滿足部署方案的約束條件,過程如圖1所示。

圖1 交叉操作示意圖

方案1和方案2交叉后,方案1的前半部分和方案2的后半部分結合形成新方案1,方案1的后半部分與方案2的前半部分結合形成新方案2。

2.4 變異

變異是在交叉后的個體中,以變異概率p m對所有個體的基因位進行變異運算,隨機產生一個0～m之間的自然數賦值給該位,生成子代群體。圖2為變異生成新方案的過程。

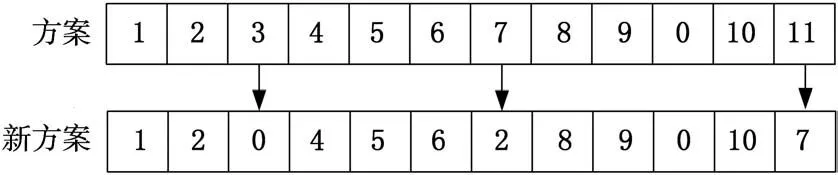
圖2 變異操作示意圖

變異生成的新個體必須滿足雷達網部署的約束條件。

3 算法流程

基于遺傳算法的組網雷達優化部署算法流程如圖3所示。

(1)根據雷達類型、數量、陣地數量,確定染色體編碼的長度;

(2)按約束條件隨機生成N個方案作為初始種群;

(3)根據實際情況計算每種方案的適應度值,并根據適應度值確定每種方案的被選擇概率,并進行排序;

(4)根據排序結果,利用遺傳算法的選擇、交叉、變異等操作準則進行群體更新,形成新一代的群體;

(5)停止準則,當最優個體的適應度和群體適應度不再上升,或達到預定的迭代次數,結束算法,輸出結果。

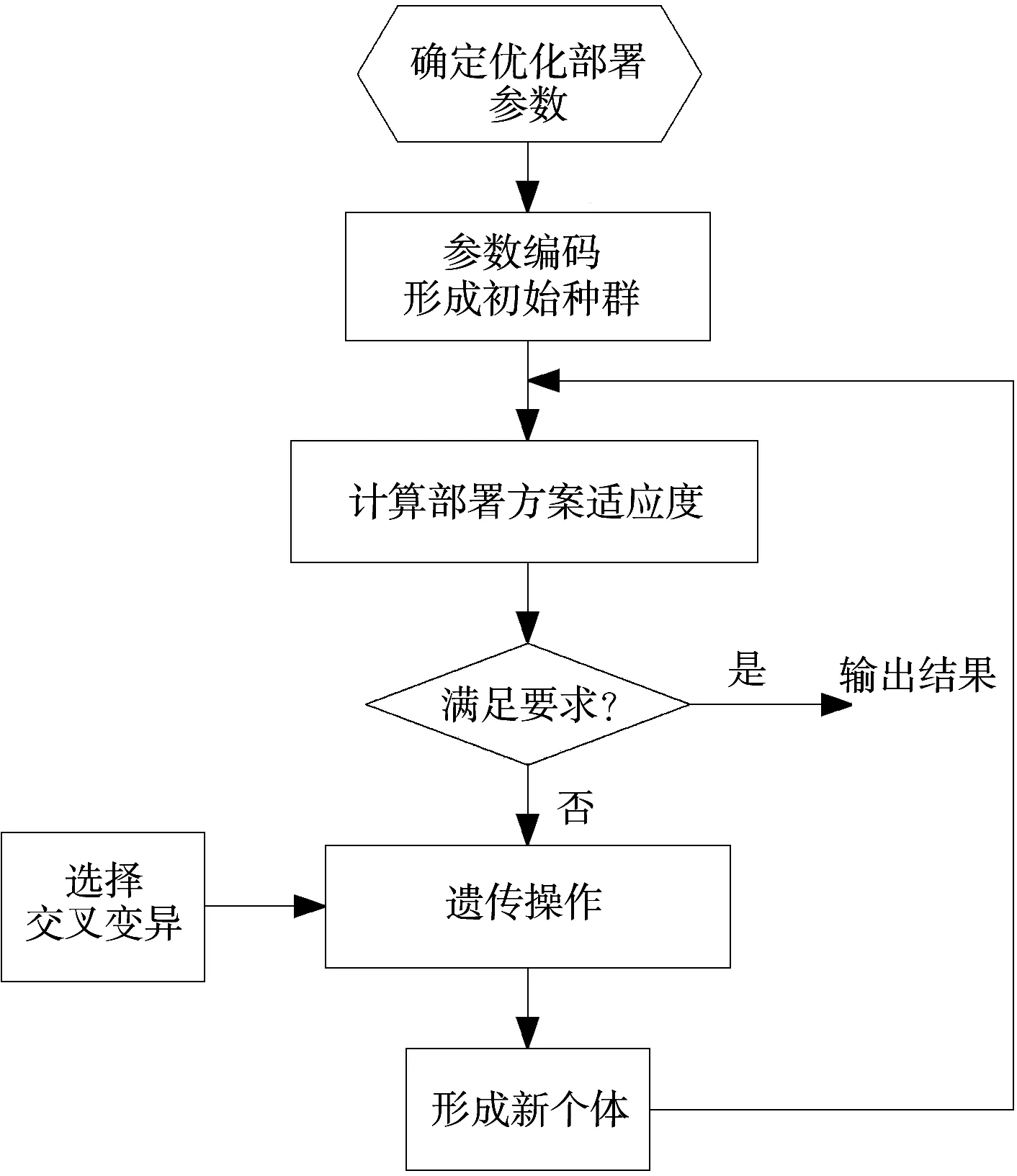
圖3 優化部署算法流程

4 算法仿真

根據前面的算法,選取7型雷達,7個陣地進行部署,各雷達陣地的約束條件如表2所示。

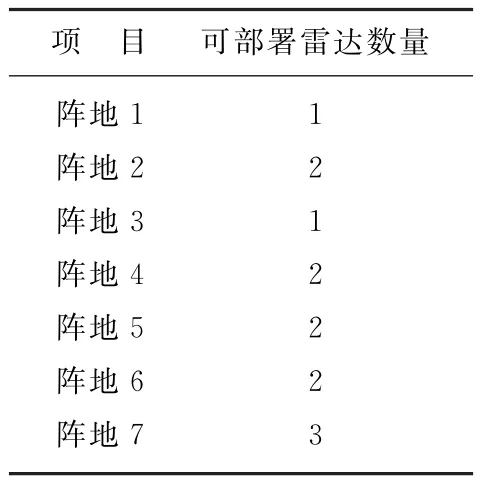
表2 約束條件表

仿真雷達探測威力參數如表3所示。

表3 仿真雷達參數

取初始種群數量為N=50,按約束條件隨機生成初始方案50個,交叉概率pc=0.6,變異概率pm=0.05,經過100次的迭代,仿真結果如表4所示。

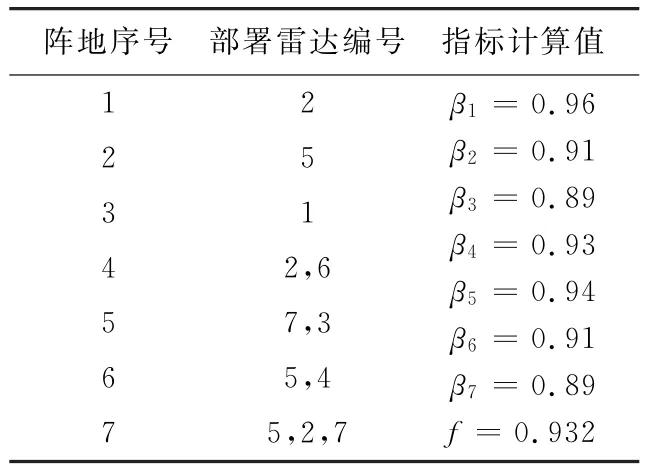
表4 仿真雷達參數

探測威力效果如圖4所示,該部署方案的綜合探測性能最佳,其目標函數值最大,在各高度層,雷達網覆蓋滿足連續性、嚴密性和重疊性要求,同時滿足雷達配置的四個一體化要求。仿真結果表明:基于遺傳算法的組網雷達優化部署方法能達到最優或準最優解,算法的執行速度比枚舉法有明顯的提高;不存在知識的組合爆炸問題,是一種有效的雷達網優化部署方法。

圖4 優化方案覆蓋效果

5 結束語

雷達組網是提高雷達系統整體探測性能,獲取信息優勢的有效手段,基于遺傳算法的組網雷達優化部署方法為組網雷達優化部署提供了一種在解空間尋優的方法,該方法原理簡單,尋優速度快,應用靈活,是解決雷達組網中優化部署問題的一種比較好的方法。為進一步提高算法的收斂性和收斂速度,需要在優化目標函數和交叉概率、變異概率等方面作進一步的研究。

[1]闕渭焰,彭應寧.數據融合與雷達優化布站[J].系統工程與電子技術,1996(12):26-32.

[2]盧金濤,楊瑞娟,熊祝平.雷達陣地選擇的多目標決策方法[J].空軍雷達學院學報,2003,17(1):13-15.

[3]莫建文,韓傳久,張彤.遺傳算法在雷達組網最優布陣中算法研究[J].信息技術,2005(3):66-68.

[4]Fogel D B.A Comparison of Evolutionary Programming and Genetic Algorithms on Selected Constrained Optimization Problems[J].Simulation,1995,64(6):397-404.

[5]Homaifar A,Qi C L,Lai S H.Constrained Optimization via Genetic Algorithms[J].Simulation,1994,62(4):242-253.

[6]Youssef H,Sait S M,Adiche H.Evolutionary Algorithms,Simulated Annealing and Tabu Search:a Comparative Study[J].Engineering Application of Artificial Intelligence,2001,14(2):167-181.

[7]張遠,曲成華,戴誼.基于遺傳算法的雷達組網誤差配準算法[J].雷達科學與技術,2008,6(1):65-68.ZHANG Yuan,QU Cheng-hua,DAI Yi.Registration Algorithm for Radar Netting Based on Genetic Algorithm[J].Radar Science and Technology,2008,6(1):65-68.(in Chinese)

[8]茍先太,金煒東.有約束優化中遺傳算法的應用[J].西南交通大學學報,1997,32(4):433-437.