基于遺傳算法的模糊綜合評價法在地下水質評價中的應用
夏哲兵,劉國東,任玉峰,劉 剛
(1.四川大學水利水電學院,四川 成都 610065;2.四川大學水力學與山區河流開發保護國家重點實驗室,四川 成都 610065)
模糊綜合評價法以其理論嚴謹、計算簡單、評價較客觀等特點被廣泛應用,但其權重的確定仍具一定的經驗性。目前模糊綜合評價的研究難點之一就是如何科學地、客觀地將一個多指標問題綜合成一個單指標形式,以便在一維空間中實現綜合評價,其實質是如何合理地確定這些評價指標的權重[1-2]。而層次分析法(AHP) 是目前一種被廣泛應用的確定權重的方法,但它自身存在的主要問題是如何構造、檢驗和修正判斷矩陣的一致性和計算判斷矩陣各要素的權重[3]。
基于上述分析,筆者提出一種利用模糊綜合評價矩陣構造適用于確定指標權重的判斷矩陣,構建了利用遺傳算法解決判斷矩陣的一致性檢驗、修正和計算權重的新模型,并將此模型應用于地下水質評價工程實例中。
1 基于遺傳算法的模糊綜合評價法
假定共有m個井的水樣資料,每個水井監測資料中有n個評價因子,以此來說明基于遺傳算法的模糊綜合評價模型的具體建模過程,主要步驟如下。
1.1 步驟1:構建評價指標
地下水質評價指標一般有總硬度、溶解性總固體、硫酸鹽、硝酸鹽、亞硝酸鹽、氯化物、氟化物、鐵和錳等,從上述指標中選取其中的n個構成評價指標。
1.2 步驟2:標準化及構造模糊綜合評價矩陣
在實際應用中,因多數地下水質評價指標都存有量綱。為確定單個評價指標的相對隸屬度,需對各指標進行標準化和無量綱化處理。為盡可能保持各評價指標值的變化信息[4],且大多數地下水水質指標是越小越優,故按如下公式處理:
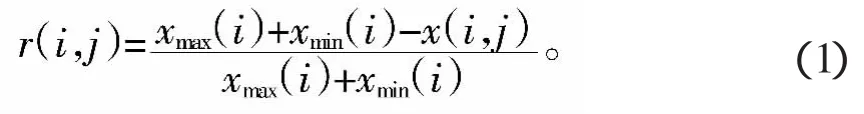
式中:x(i,j)為第j個水樣中第i個評價指標的實測值;xmax(i)、xmin(i)和xmid(i)分別為第i個指標的最大、最小和中間值;r(i,j)為x(i,j)標準化后的數值,也叫做相對隸屬度值,i=1~n,j=1~m。由計算出的r(i,j)作為矩陣元素,構建模糊評價矩陣R=(r(i,j))n×m。
1.3 步驟3:構造判斷矩陣
為減少甚至避免信息的不對稱,引入各評價指標的樣本標準差。樣本標準差用公式(2)表示,其可體現各評價指標之間的差異和反映評價指標對綜合評價的影響程度,根據公式(3)可構造判斷矩陣B[5]。
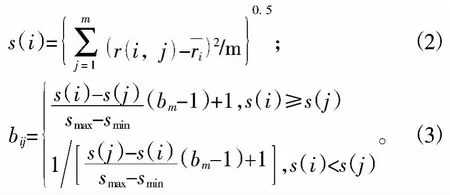
式中:bij為判斷矩陣B中的元素;bm為相對重要性程度參數值;smax為s(i)中最大的數;smin為s(i)中最小的數。bm=min{9,int[smax/smin+0.5]},min為取最小值函數,int為取整函數。
1.4 步驟4:權重計算過程
判斷矩陣B的一致性檢驗、修正及其權重的計算,要求滿足ai> 0和Σai=1 (i=1~n)。根據判斷矩陣B的定義,理論上有[5]:
試驗數據采用Excel2007進行整理。整理后數據采用SPSS17.0統計軟件進行One Way Anova方差分析。

此時,B應具有性質[5-6]:①bii=ai/ai=1;②bji=aj/ai=1/bij(i,j=1~n);③bijbjk=(ai/aj)(aj/ak)=ai/ak=bik(i,j,k=1~n)。其中:①單位性;②倒數性;③傳遞性,也為①與②的充分條件。
現在的問題就是用已知判斷矩陣B,來推求各評價指標的權重值ai。若判斷矩陣B滿足公式(4),決策者能精確度量ai/aj,即bij=ai/aj,判斷矩陣B具有完全的一致性,則有[7]:

在現實評價系統中,具有完全滿意一致性的判斷矩陣是幾乎不存在的。在實際應用時,只需判斷矩陣B滿足一定精度要求,即滿足一致性(CIC(n) <0.1) 即可。如果B不滿足上述要求,則需根據實際情況進行修正。假定修正后的判斷矩陣用Y表示,修正后的判斷矩陣的權重值仍為ai,則稱使公式(6)最小的Y矩陣為B的最優一致性判斷矩陣[3]。
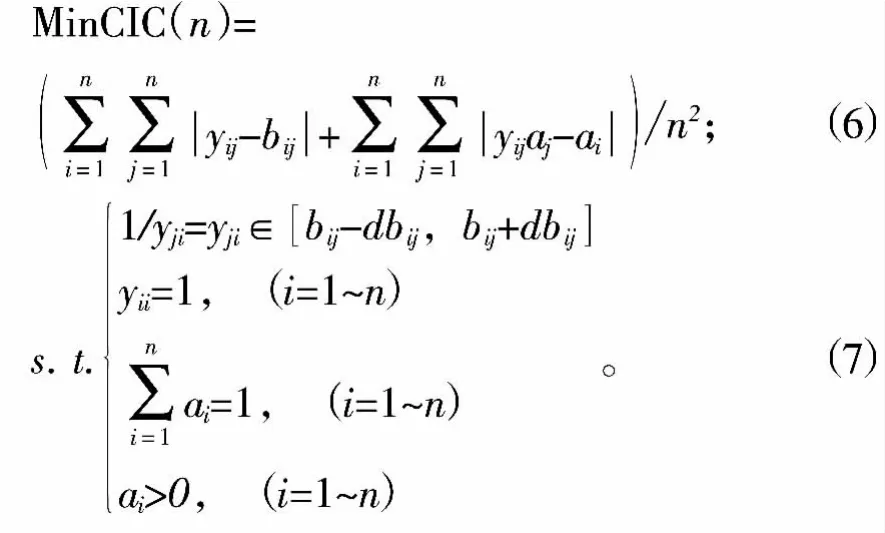
公式(6) 中的目標函數CIC(n) 為一致性指標系數,公式(7)為約束條件。d是不小于0的參數,可根據經驗,按從小到大的原則從(0,0.25]內進行選取。
從公式(6)可以看出,目標函數是一個較復雜的非線性優化函數,非常規數學方法是可以解決的。其中權重值ai和修正判斷矩陣Y的上三角矩陣元素均為優化變量,對n階判斷矩陣B而言,共有n(n+1)/2個獨立的優化變量[7]。基于遺傳算法具有出色的全局尋優功能,用它來求解公式(6)較為簡單。遺傳算法的步驟可參見文獻[2]。
1.5 步驟5:模糊綜合評價計算
通過遺傳算法計算出最優解即為各評價指標的權重,將權重向量矩陣與模糊評價矩陣R進行復合運算,即求得地下水質綜合評價結果矩陣Z。

式中:運算符號“·”為矩陣乘法,即把權重值與相對隸屬度相乘并累加。綜合評價值z(j)越大,說明第j個水樣井的水質越好,據此可對地下水質的優劣做出科學的評價。
2 實例應用
2.1 研究區概況
本次研究區域位于內蒙古鄂爾多斯的烏審旗圖克鎮,地處毛烏素沙漠北邊緣,地理位置為東經109°29′,北緯39°03′。圖克鎮屬溫帶大陸性氣候,受蒙古高氣壓影響極大,西北冷空氣控制時間長,年平均氣溫為6~8℃。具有干旱多風、氣候干燥、溫差變化大等特點。當地降水稀少,年平均降水量為375 mm;蒸發量大,年平均蒸發量為2 592 mm。
2.2 計算過程
數據來源于內蒙古鄂爾多斯烏審旗圖克鎮煤化工工業園區地下水水質監測報告。
依據步驟1及對地下水監測資料進行對比分析,最終確定6個水質指標(即總硬度、溶解性總固體、氯化物、硫酸鹽、氟化物、鐵)作為評價指標,構建評價指標X=(總硬度,溶解性總固體,氯化物,硫酸鹽,氟化物,鐵)。
上述評價指標均屬越小水質越優型,按公式(1) 進行標準化計算。以總硬度為例,計算該評價指標對7#水井的相對隸屬度,結果如下:
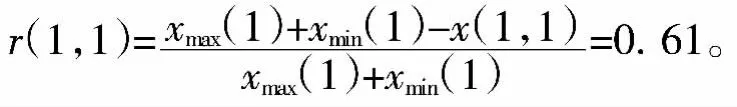
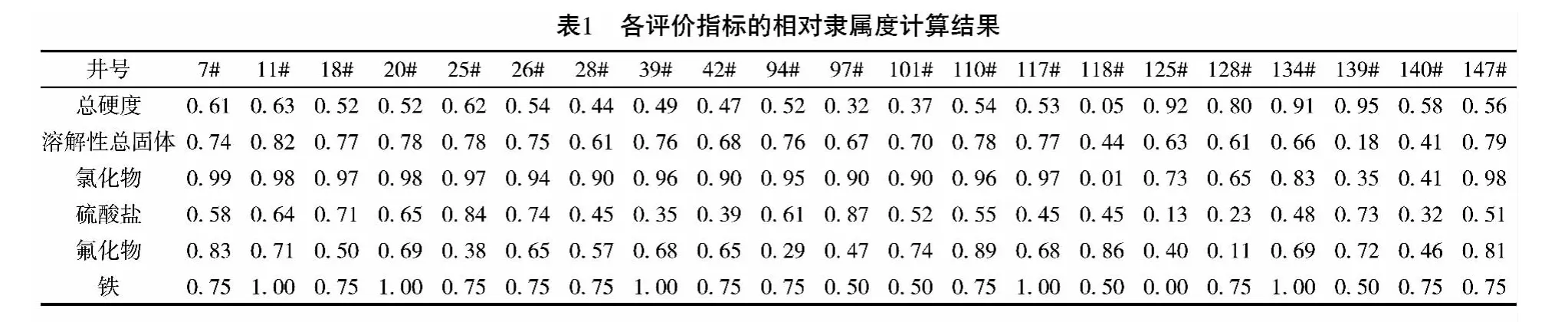
以此類推,計算出所有評價指標對井的相對隸屬度值,并用隸屬度值構建模糊評價矩陣R,計算結果列于表1中。
?
根據步驟3計算出樣本標準差s(i)(i=1,2,…,6) 分別為0.202、0.153、0.254、0.187、0.195、0.230,相對重要性程度bm=2.0。通過公式(5),構建判斷矩陣B如下:

針對步驟4,具體實現過程借助Matlab7.0軟件進行編程,取各指標權重的變化區間為(0,1),參數d取為0.2[7]。借助遺傳算法選擇200次,加速10次,得到評價指標1~6的權重值分別為:0.160、0.110、0.237、0.142、0.151、0.200。與之對應的目標一致性系數CIC(n) =0.000 8<0.1,表明該判斷矩陣具有滿意一致性。而且指標3(氯化物)、指標6(鐵) 和指標1(總硬度)所占的權重相對較大,與區域實際情況較為相符。
2.3 模糊綜合評價結果
由計算出的權重指標,構建指標權重矩陣為A= (0.160,0.110,0.237,0.142,0.151,0.200)。根據步驟5,求得水質綜合評價矩陣Z(j)= (0.771,0.821,0.724,0.800,0.741,0.745,0.651,0.742,0.667,0.672,0.633,0.635,0.762,0.766,0.353,0.469,0.548,0.787,0.567,0.500,0.754)。
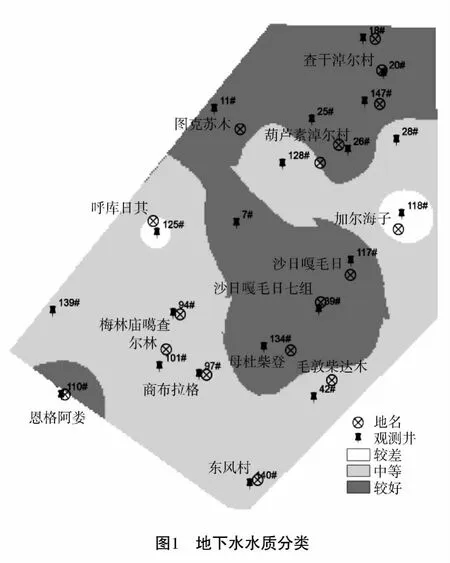
根據最大隸屬度原則,可見位于11#和20#處的地下水質為最優,位于118#和125#處的水質為最差。各水井地下水質的優劣情況見表2。

?
為了說明模型在地下水質評價中的可行性及精度要求,采用F值評分法對地下水質數據進行處理,處理結果見表3。

?
通過上述對比分析知,本方法的綜合評價結果與F值評分法基本一致。但F值評分法所得的數據結果分層不明顯,而本方法的數據結果分層明顯,對管理者而言有利于做出最正確的決策。根據計算成果,需對上述水質較差的區域,采取地下水環境保護措施。
3 可視化計算成果
基于Arcgis具有強大的空間分析功能和顯示功能[8]。利用Arcgis的專題圖功能,采用按值渲染的方法,將本次綜合評價結果以電子地圖的形式顯示出來,得到區域地下水質分類圖,見圖1。
4 結束語
1)利用模糊綜合評價矩陣構建適用于確定指標權重的判斷矩陣,并采用遺傳算法對判斷矩陣一致性進行檢驗、修正及確定權重的新模型,避免了因人而異產生的主觀臆斷性,并將該模型成功應用于地下水質評價中。
2)通過對烏審旗圖克鎮地下水監測資料進行實例分析表明,采用該方法計算出的水質優劣排序結果合理、客觀,且操作簡單、精度高,具有實際應用和推廣價值。
3)本次評價指標是人為篩選之后確定的,在今后的評價中采用何種指標需進一步研究。
[1]許國志,顧基發,車宏安.系統科學[M].上海:上海科技教育出版社,2000.
[2]金菊良,丁晶.水資源系統工程[M].成都:四川科學技術出版社,2002.
[3]劉澤雙,章丹,康英.基于遺傳算法的模糊綜合評價法在科技人才創新能力評價中的應用[J].西安理工大學學報,2008(3):376-381.
[4]陳守煜.復雜水資源系統優化模糊識別理論與應用[M].吉林:吉林大學出版社,2002.
[5]汪應洛.系統工程[M].2版.北京:機械工業出版社,2001.
[6]金菊良,魏一鳴,付強,等.計算層次分析法中排序權值的加速遺傳算法[J].系統工程理論與實踐,2002,22(11):39-43.
[7]金菊良,魏一鳴,丁晶.基于改進層次分析法的模糊綜合評價模型[J].水利學報,2004(3):65-70.
[8]張成才,李紅偉,吳瑞鋒,等.基于GIS的水質模糊綜合評價方法研究[J].人民黃河,2009,31(5):52-53.

