凍融循環引起的飽和孔隙組合轉換模擬研究
Aleksander S.Kurilko,Vladimir I.Popov
(俄羅斯科學院西伯利亞分院北極礦業研究所,雅庫茨克677980,俄羅斯)
0 Introduction
Experimental results[1-5]showed that freezing of rocks depends on the porosity and their water saturation.The most destructive effect occurs when freezing the samples in an aqueous medium,i.e.with full water saturation pores[3].
Rock can be represented as a model microporous medium with a given number density distribution of pore radius-r[6].When watersaturated environment resulting from the phase transition is an increase in the initial volume of water in the pore by an amount proportional to the bulk phase expansion coefficient αf.
Kinetic equation for the density of the pore size distribution depending on the number of cycles of freezing-thawing(t)can be represented in the form
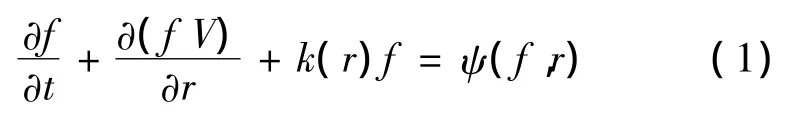
where f—the number density distribution of pore radius-r.
Here the second term denotes the change of f due to increase of pore radius in one cycle of freezing.Thus the growth rate of the radius of the pores in one cycle is defined as:
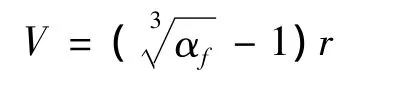
1 Materials and methods
And the second term of equation(1)can be interpreted as the convective motion of the distribution function of pores in the size space radii[7].The third term of the equation determines the growth of the real density distribution function of pore in radius of the irreversible plastic deformation area,on the principle of inheritance of traits i.e.it is proportional to distribution function-k(r)f(r,t).The coefficient k(r) can determine the preferential growth of the number of pores of a certain size(radius)of this mechanism.Term of the equation on the right side of the equation is the sum of sources and sinks for the density distribution of the pores radius-r as a result of the coalescence pair process.
As the most likely,we will consider the interaction of closely spaced pores,and we will explore two options of“reactions”determing the“source of pores-i?and”sink of pores-i?for this size class-ri.Here we take into account the conservation of the total pore volume,as a result of coalescence“reactions”,a total pore volume should be maintained.Therefore,as a result of“reaction”of pore coalescence with radius riand rj,we have to keep the volume:
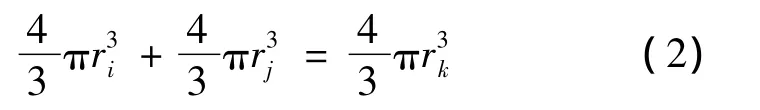
hence:
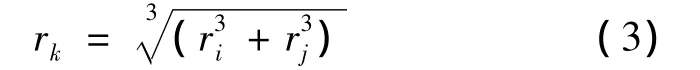
I.e.as a result of interaction(coalescence)(n) of pores riand(n)pores rjan equal pore number(n) sorts riand rjdissapears,but appears(n)pores with radius rk.This reaction will characterize an escape of pores from size class with a radius ri.
The situation is somewhat different when building a source far ri,in this case as a result of interaction (coalescence)of pores rland rj.There should appear pores ri.This condition imposes certain restrictions on the radius of interacting pores.Therefore we have for the volume:
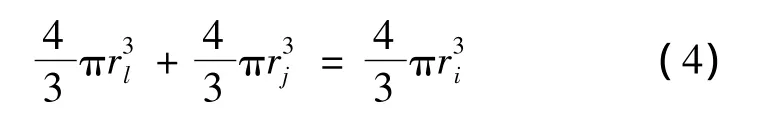
where we find the expression for the pore radius rl,which,while interacting(coalescence)with pore rjwill gave us pore ri.
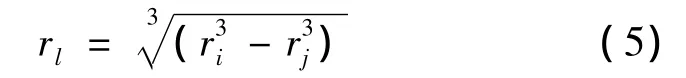
In accordance with the expressions given above,as the result of the coalescence reaction(n),and then rj(n)is formed then rl(n)then ri.The rest of the expression does not change.Condition of pore coalescence rMand rLis a complex event consisting of several steps-firstly,from finding their centers at a distance apart rM+rL.Probability of this event is defined as the probability to find the nearest neighbor at a given distance[8].

where N=f(rM,t)dr+f(rL,t)de the total number of pores with sizes rM,and rL.
The second stage of this process is,that the pores rMand rLmake contact.The probability of this event is equal to the product of pore concentrating rMrLin this volume.Put the case in the following way;

Here
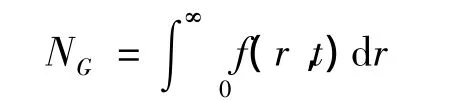
is a total number of pores in a given volume.
In conclusion,we introduce the matrix W of transition probability-Wijk,which mean that as a result of contact interaction(reaction)of pore with a radius riand pore with a radius rjthe pore with a radius rkis formed.For coalescence reactions of the type(2)and considering the partial disappearance of the two reactants of probabilities of these complex events have following form
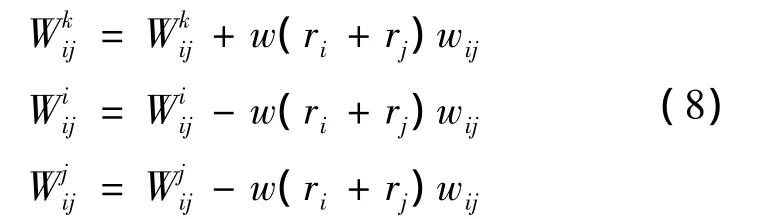
For coalescence reactions of the type(4)also considering the partial disappearance of the two reactants of probabilities of these complex events have the form of

The final expression for the transformation of density of radial pore destribution for converting processes to keep the volume will be

where s is normalizing factor.Then the formula of the kinetic equation for k-a function component of numerical distribution density of pores on the radius in the material exposed to sign-variable temperatures(cycles of freezing-thawing)will be:
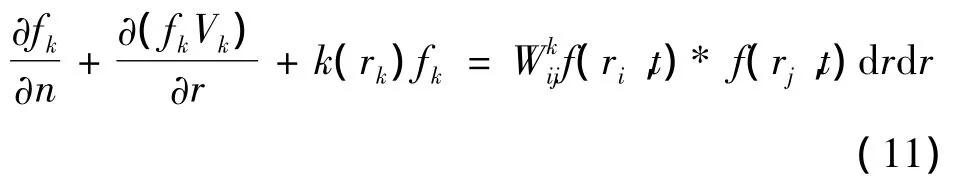
For further calculations we make the following simplifying assumptions:
any initial pore size distribution can be represented by superposition normal to their mean value rcpand variance rd,
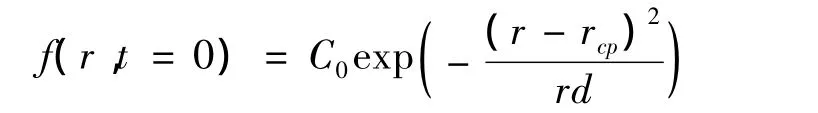
in some simple cases with an uniform distribution.Numerical volume density of pore size distribution per unit of volume must satisfy the initial time t=0 to the condition of normalization
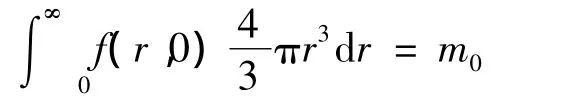
where m0—is the initial porosity of the material.
Fig.1-2 presents the results of calculations of conversion of pore assembly while interaction of sign-variable temperature neglecting the second and the third terms in the left-hand side of equation(1)(Vk=0;k (rk)=0).
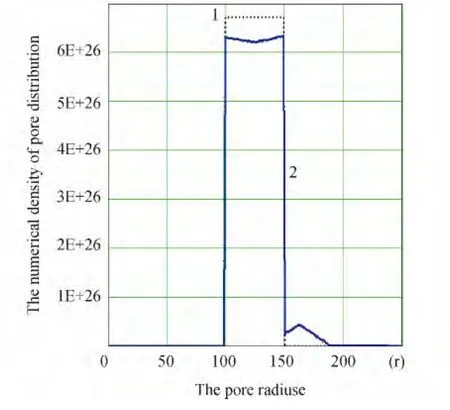
Fig.1 Transformation of the initially homogeneous number-density distribution of pores by the size after influence of 100 cycles of sign-variable temperature influence
In Fig.3-4 shows the results of modeling of alternating influence on monoporous medium.Monoporous medium was modeled by sufficiently narrow uniform distribution-Fig.3.Also the monitoring of conservation of total porosity as a result of conversion processes was carried out(Fig.4).A characteristic feature of transformations monoporous assembly of pores is the splitting of initial allocation on number of separates in accordance with reaction(2).
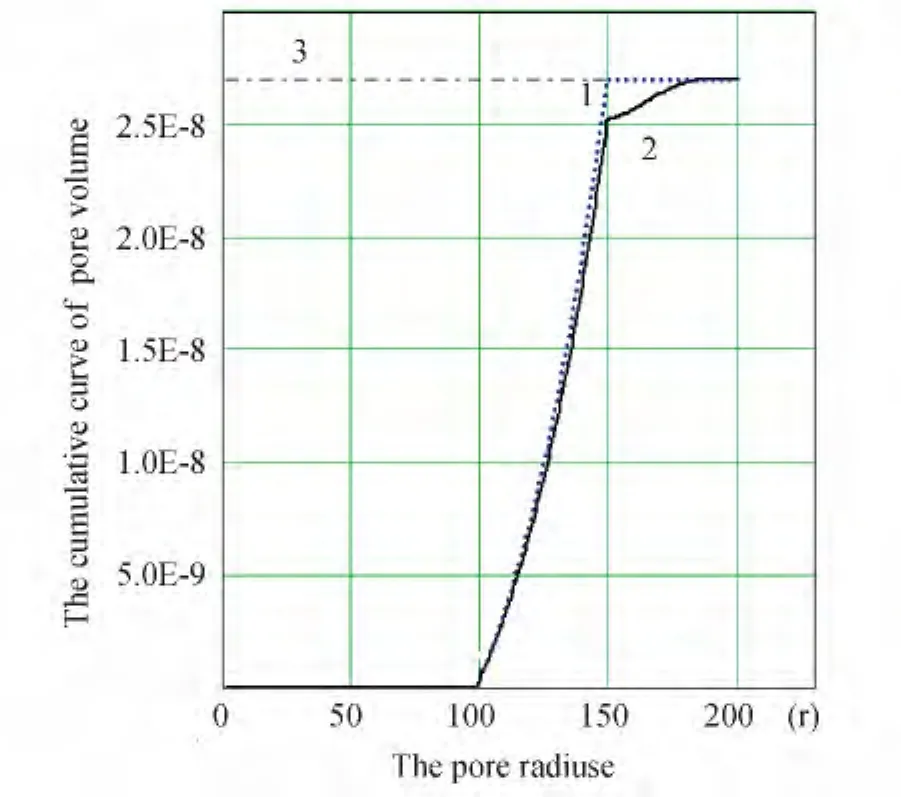
Fig.2 Change of cumulative porosity of the initially homogeneous number-density distribution of pores by the size after influence of 100 cycles of sign-variable temperature influencecurve 1-initial distribution;curve 2-after 100 cycles; curve 3-monitoring of porosity throughout influence
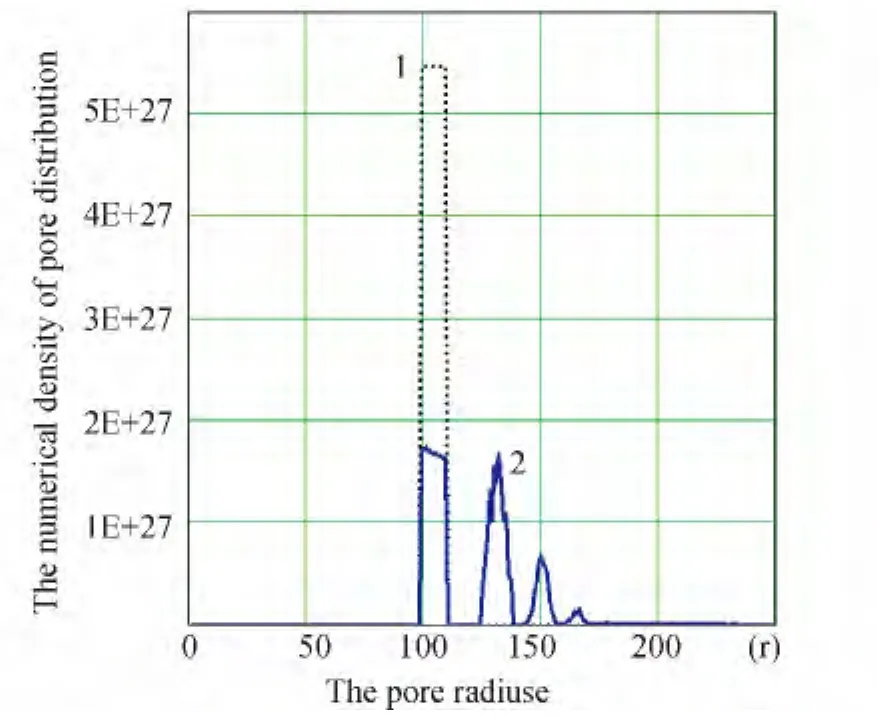
Fig.3 Transformation of the initially homogeneous monoporous number-density distribution of pores by the size after influence of 100 cycles of sign-variable temperature influence
Fig.5 presents the results of experimental(BET) determine of the distribution of the cumulative pore volume and differential pore-size distribution by volume of kimberlite samples at baseline and after 3 cycles of sign-variable temperature exposure.Fig.6 shows the results of modeling of a differential pore-volume distribution by size in samples of kimberlite in the initial state(1)and after 3 cycles of sign-variable temperature exposure(2).Values of the coefficients of the model(11)and the following input parameters are V= 0.03ri,k(r)=0.015;m0=0.027;s=100.
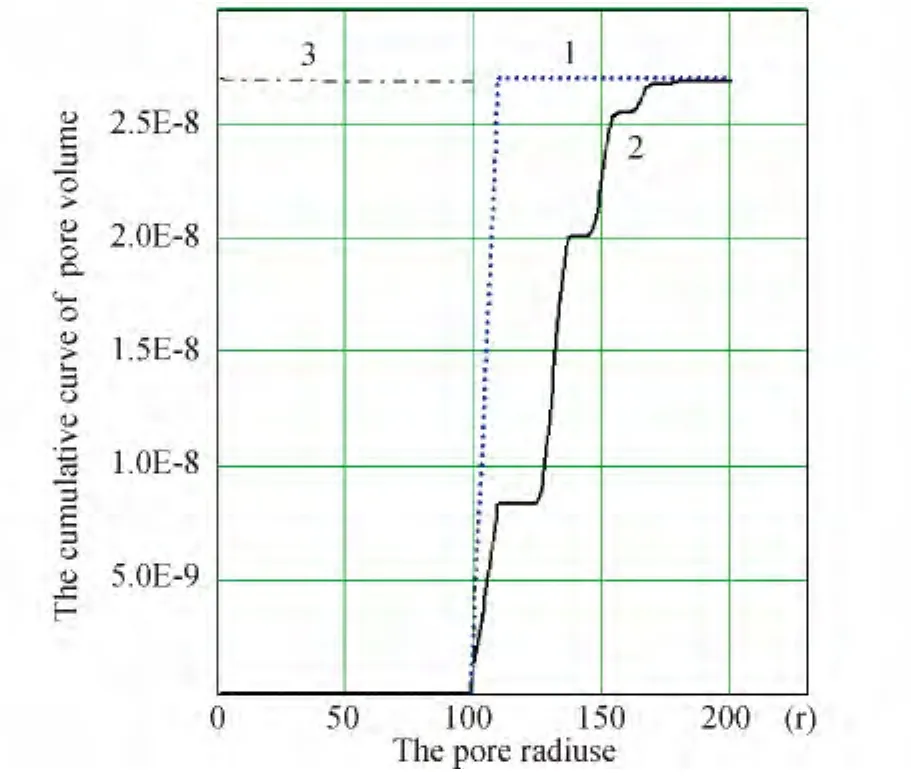
Fig.4 Change of cumulative porosity of the initially homogeneous monoporous number-density distribution of pores by the size after influence of 100 cycles of signvariable temperature influencecurve 1–initial distribution;curve 2-after 100 cycles;curve 3-monitoring of porosity throughout influence.
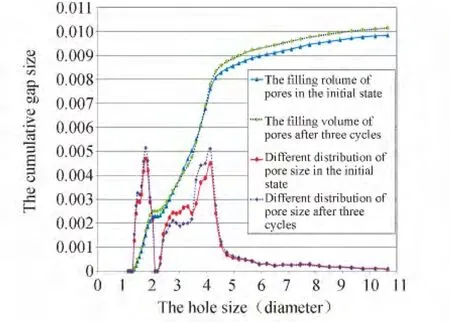
Fig.5 Results of the experimental definition of differential distribution of pore volume on size and corresponding cumulative pore volume
Fig.7 shows-initial distribution(calculated on the basis of the experimental curve of Fig.5)of the numerical density of the pore on radius for kimberlite sample (curve 1)and after three cycles of exposure to signvariable temperatures(curve 2).Fig.8 shows the distribution of the corresponding curves of cumulative volumes of pores.
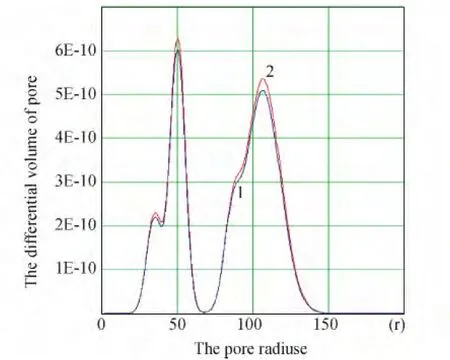
Fig.6 Results of modeling of differential distribution of pore volume on size of initial(1)and after 3 cycles of sign-variable temperature influences(2)
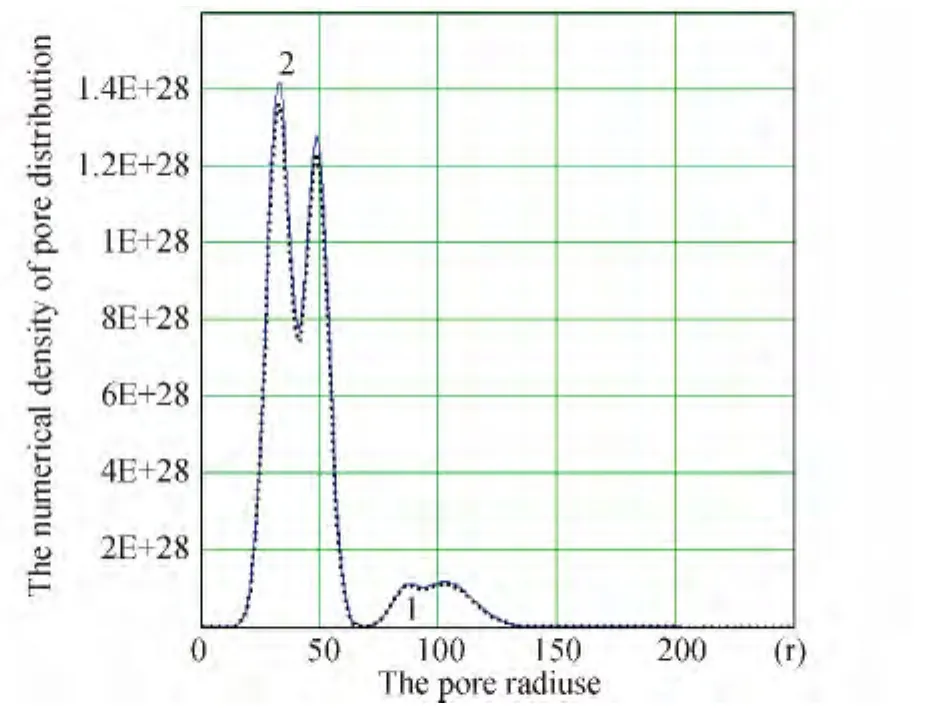
Fig.7 Distribution of pore on radius1 initial;2 after three cycles of sign-variable temperature influence
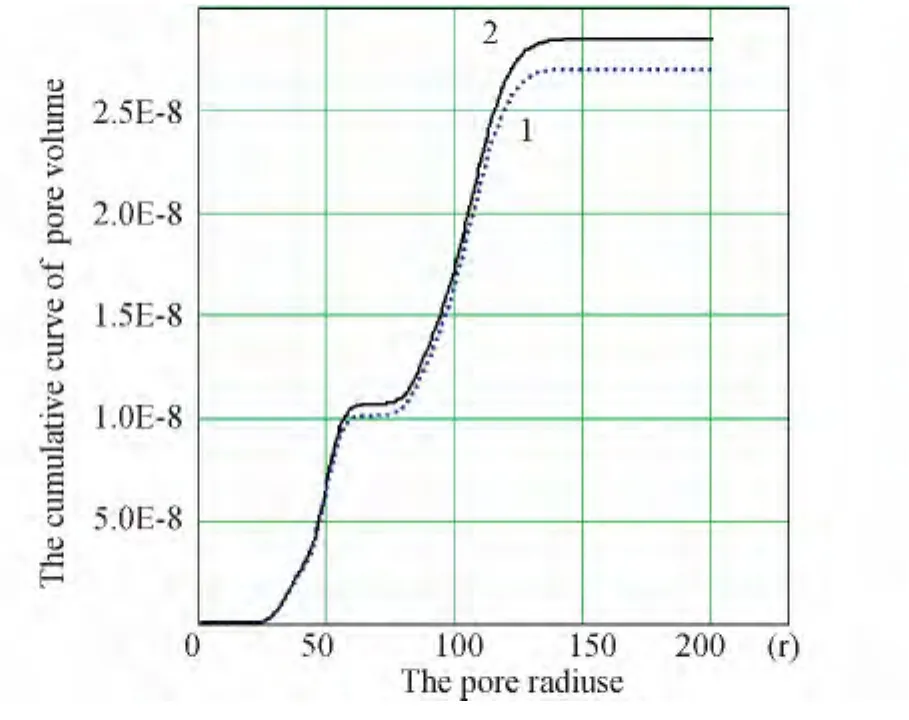
Fig.8 Distribution of cumulative curves of pore volume1-initial;2-after three cycles of sign-variable temperature influence
2 Discussion and conclusions
The represented results adequately reflect the processes of growth and transformation of the pore assembly under sign-variable temperature influences.Modeling conversion of initially homogeneous monoporous density of distribution of pore on sizes after exposure of sign-variable temperature cycles meets the conditions of conservation of volume and not physically inconsistent.Increase of the large pores content under sign-variable temperature influences is confirmed by the results of experimental studies[9].
[1] Kurilko A S,Popov V I.O Predvaritel'noy klassifikatsii obraztsov gornykh porod po nachal'noy poristosti pri is pytaniyakh na morozostoy-kost'[J].Gornyy informatsionno-analiticheskiy byullyuten' GIAB.2008,(7):227-230.
[2] Yershov Ye D.Vlagoperenos i kriogennyye tekstury v dispersnykh porodakh[M].I.:Izd-vo MGU,1979:214-216.
[3] Kurilko A S,Popov V I.Issledovaniye prochnosti porod posle vozdeystviya tsiklov zamorazhivaniya-ottaivaniya[J].GIAB,2004,(9):132-134.
[4] Shesternev D M.Kriogipergenez krupnooblomochnykh i geotekhnicheskiye svoystva porod kriolitozony[M].Novosibirsk:Izd-vo SO RAN,2001:266.
[5] Savel'yev B A.Fizika,khimiya i stroyeniye prirodnykh l'dov imerzlykh gornykh porod[M].Novosibirsk:Izd-vo MGU,1971:508-514.
[6] Kurilko A S,Popov V I.Imitatsionnaya model'protsessa preobrazovaniya sfericheskikh por pri tsiklicheskom kriogennom vozdeystvii na gornyye porody[J].Gornyy Informatsionno-Analiticheskiy Byulleten',2010(9):301-305.
[7] Shapiro A H,Erickson A J.On the changing size spectrum of particle clouds undergoing evaporation,combustion,or acceleration[J].Transactions of the ASME,1957,79(4):775-788.
[8] Chandrasekar S.Stokhasticheskiye problemy v fizike i astronomii[M].IL,1947:168-172.
[9] Takarli M,Prince W,Siddique R.Damage in granite under heating/cooling cycles and water freeze-thaw condition/Int[J].J Rock.Mech.Min Sci,2008,45:1 164-1 175.
- 黑龍江大學工程學報的其它文章
- The harm of perennial frozen soil to the pipeline exporting the crude oil from Mohe county to Daqing city
- Overview of research methods of frozen soil hydrology in Heilongjiang Province
- Environmental geochemistry of urban areas in Yakutia
- A permafrost factor in the development of deformations on the Amur Highway
- The problem of project statement of construction principles of buildings and facilities in permafrost
- The forecast of a temperature regime of soils containing the pile foundation of a pithead on diamond-mining mines of cryolithic zone

