電力系統中長期穩定分析用聯合供水水電機組非線性仿真模型

，， ，，

(國網四川省電力公司電力科學研究院，四川 成都 610072)

特殊的地理條件使得一些水電站使用長引水涵洞與上游水庫相連，并在涵洞下游末端采用分叉壓力鋼管。由于水輪機出力由水頭和流量共同決定，因此共用引水管段的水力耦合特性導致末端水電機組出力和調節特性存在關聯作用。這對電力系統的AGC控制、安控布置以及中長期穩定過程等均帶來一定程度的影響。

要準確分析水電廠在擾動后的動態響應及對電力系統的影響，必須依賴全過程動態仿真中控制保護和動態元件的模型準確度[1]。但目前對于含長引水系統的一管多機水電站仍缺乏準確的計算模型。電力系統暫態仿真程序廣泛使用的理想水輪機模型和剛性水擊模型僅適用于一管一機系統[2]。全過程動態仿真程序[3]雖然提供了一管多機水輪機模型，但該模型不能計及長引水管道條件下調壓井的動態響應對機械轉矩的影響。針對大擾動下水電站動態特性對系統行為的影響，IEEE聯合工作組于1992年提出了包括剛性水擊、彈性水擊的單引水管水輪機模型和共用引水管水輪機模型[4]，為電力系統的仿真計算提供了有力參考。而后陸續有文獻[5-6]針對不含調壓井的一管多機系統的建模和解耦控制問題開展研究。實際應用中，針對共用長引水管道水電機組，必須綜合考慮調壓井和涵洞中的水力耦合作用對動態過程的影響，現有模型庫無法滿足該需求。

圖1 含調壓井的水力系統

基于理論推導，提出一種共用長引水系統的水電機組仿真模型，綜合考慮調壓井和長引水隧洞水力過程對機組動態特性的影響，仿真結果與實測數據的對比表明，模型能夠正確反映中長期過程中水電機組的動態響應。

1 含調壓井的彈性水擊模型

對于任意一段引水管道，考慮水管的彈性后，由水力方程[7]

(1)

可解得

(2)

式中，Ha、Hb分別為水管兩端的水頭;Qa、Qb為兩端流量；Te為水管的彈性時間，由管長L與波速a決定，即

(3)

式中，α由管壁厚度、管道面積、水體壓縮模量、管材彈性模量等因素決定。

對圖1中的涵洞，運用式(2)，并以標幺值方式表示，有

hr=hwsech(TeTs)-ZTqTtanh(TeTs)

(4)

涵洞上游端的水頭偏差為0，即hw=1，因此式(4)寫為

hr=1-ZTqTtanh(TeTs)

(5)

再利用涵洞與調壓井和分叉管間的流量關系，有

qT=qr+q1+q2+q3

(6)

忽略調壓井中的波動過程，有調壓井流量和水頭間的關系

QrΔt=(Hr-Hr0)Sr

(7)

則

(8)

以標幺值和微分算子表示式(8)，有

qr=sTshr

(9)

式中，Ts為調壓井的溢水時間常數，Ts=Sr=調壓井面積。

將式(6)、(9)代入式(5)得

(10)

同樣對每條分叉管，應用式(4)，可得

hi=hrsech(Teis)-Ziqitanh(Teis)(i=1,2,3)

(11)

式中,Tei(i=1,2,3)分別為3條分叉管的彈性時間；Zi(i=1,2,3)為3條引水管的水力阻抗，因此

-Ziqitanh(Teis) (i=1，2，3)

(12)

上式不適應于大規模電力系統仿真計算，因此考慮對模型進行降階處理。

2 降階模型

因為

(13)

則當n=0時，

tanh(Ts)=Ts

(14)

即假設水柱是無彈性的，針對圖1中水力系統，可將式(4)改寫為

Hr=Hw-ZTQTTeTs

(15)

再考慮調壓井水頭和流量的關系以及涵洞與調壓井和分叉管間的流量關系，可推導出

(16)

由于涵洞上游水庫水頭偏差為0，則

(17)

對每個分叉管而言

(18)

設Qi0(i=1,2,3)為各分叉管的額定流量，定義qi(i=1,2,3)為對應的流量標幺值。

(19)

則式(17)和式(18)變換為

(20)

即

(21)

令HB為額定水頭，并令HB=HW，式(21)兩邊同除以HB，有

(22)

令

(23)

Twti、Twpi、Csi分別為以3條引水管額定參數規格化的涵洞、分叉管水錘時間常數和調壓井溢水時間常數，則

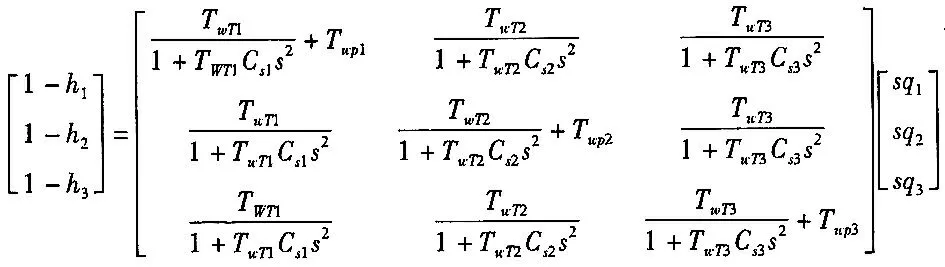
(24)

由此可建立含調壓井和分叉管的水輪機模型，當圖1中3條分叉管的參數一致時，其仿真模型可以圖2中框圖表示。

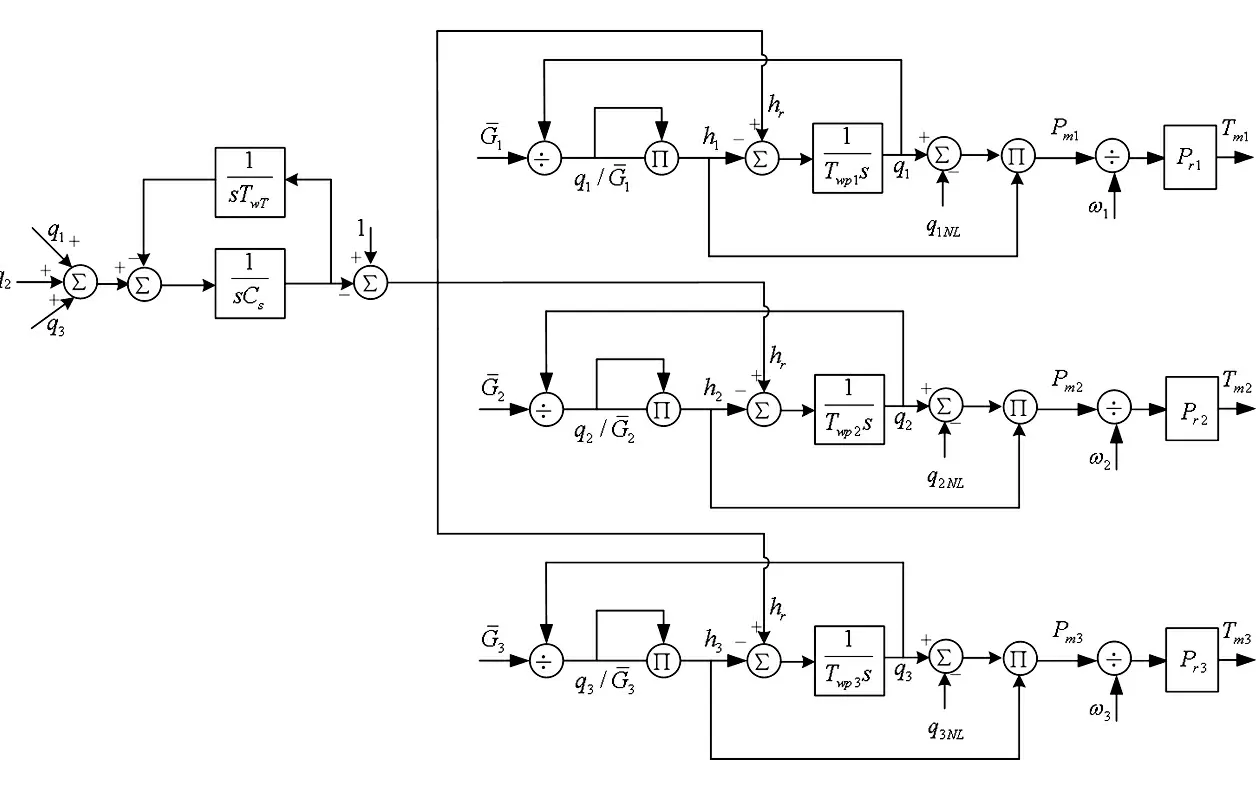
圖2 共用長引水管道的水輪機模型

3 特殊調壓井的處理

圖1中調壓井尺寸均勻，上下孔徑一致，實際許多水電站的調壓井可能由豎井和上室組成，并且調壓井連接管與豎井內徑也不相同，如圖3所示。對于圖3所示的阻抗式調壓室，由于水流在阻抗孔口處消耗了部分能量，可以有效減小調壓井中水位波動振幅。但阻抗的存在，也導致水波不能完全反射，使得壓力引水管道受到水擊的影響。

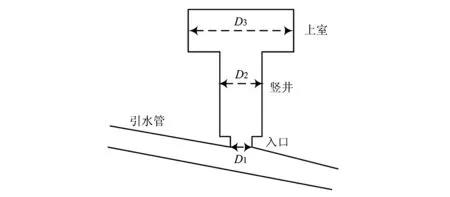
圖3 阻抗型調壓井模型

特殊的結構使得調壓井的阻抗系數很難確定，并且其值也隨著過渡過程中流量、水位等不斷變化。在水力過渡過程計算中，調壓井阻抗系數一般依據Gardel公式、模型試驗和CFD[8-10]計算來取值。對于電力系統時域仿真而言，需要阻抗系數隨工況動態取值，利用顯式公式表示不但繁雜而且也無法準確表示某些特殊結構下的準確值。這里提出調壓井結構系數k，動態修正調壓井溢水時間常數，以模擬過渡過程中壓力引水管道受到阻抗口影響的水頭變化。

圖4所示為含結構系數k的引水管和調壓井部分仿真模型，Cs為豎井段的溢流時間常數，結構系數k隨調壓井水頭變化，準確值可通過機組甩負荷試驗或詳細的流體力學計算獲得。簡單起見，可利用分段函數近似表示k為

(25)

式中，h1、h2分別表示了調壓井在不同截面積處的高度。

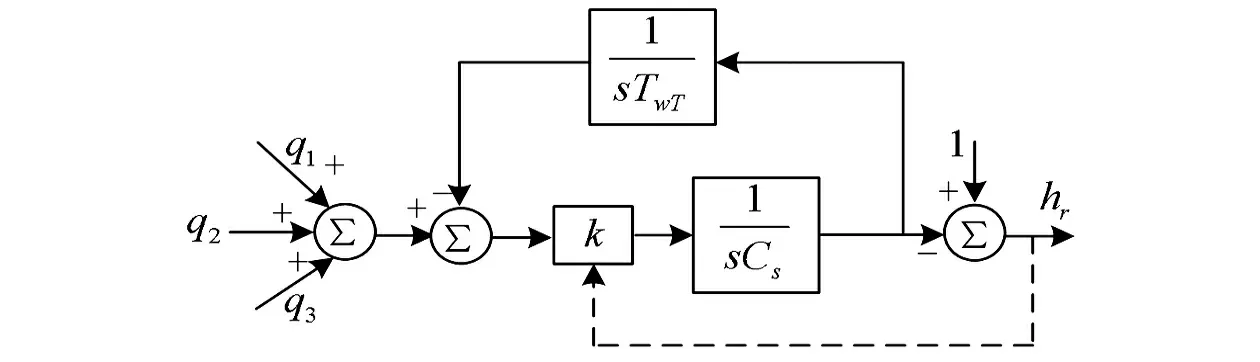
圖4 含結構系數的引水管和調壓井模型

4 仿真計算

算例1：某采用一管三機的水電站，其額定水頭92 m，單機引用流量62 m3/s，引水隧洞長22.975 km，襯砌后截面積45.3 m2，圓筒型調壓井內徑22 m，壓力鋼管內徑5.8 m，總長391.3 m。試驗運行工況為：3號機停機，1號、2號機以開度模式運行，一次調頻功能投入，1號機AGC退出運行，2號機AGC閉環。

圖5、圖6中虛線分別為1、2號機在2號機AGC閉環試驗時的機組有功功率曲線。可見，由于1、2號機共用引水隧洞，2號機快速降出力，導致水壓升高，使得1號機在定開度模式下出力明顯抬升，抬升峰值接近機組額定功率的20%。由于該電廠AGC只下發一次AGC指令，監控系統在功率到位后即退出功率閉環，因此機組間的水力耦合將影響到電廠AGC的執行精度。

由于試驗中機組調速系統采用開度模式，并且功率調節過程中一次調頻未參與動作，因此圖5中功率曲線代表了該復雜引水系統在受擾后的響應，能夠反映引水系統和水輪機的動態特性。按照式(23)計算機組參數，并采用圖2所示模型模擬引水系統和水輪機，仿真結果如圖5、圖6所示。可見仿真結果與實測曲線吻合較好。

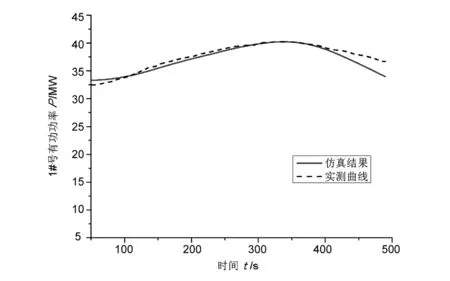
圖5 1號機組有功功率曲線

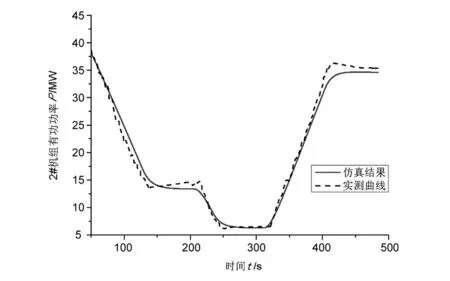
圖6 2號機組有功功率曲線

算例2：某采用一管兩機系統，其額定水頭288 m，單機引用流量232.5 m3，引水隧洞長度16.67 km，襯砌后截面積100.1 m2，阻抗型調壓井、豎井段直徑21 m，壓力鋼管內徑6.5 m，長度584 m。該電站為某特高壓直流輸電工程的龍頭電站，其特殊的引水隧道和調壓井結構對電力系統動態過程具有較大影響。

圖7所示為某次直流雙極閉鎖故障下2號機組安控切機后的1號機組功率曲線。由于2號機組斷路器動作后迅速關閉閥門，導致1號機水壓升高，造成機組出力抬升，峰值接近額定容量的21%。由于機組容量大，在系統中地位重要，1號機的動態響應特性加大了事故后交流斷面功率越限的風險。并且，該電站作為直流工程的配套電源，某些方式下可能采取孤島運行方式，其引水系統的動態過程也將對直流送端孤島系統的頻率穩定性產生影響。

采用含結構系數的調壓井和引水系統模型，并采用分段函數近似描述結構系數k，建立該電站的仿真模型，按照故障前方式設置模型運行條件，仿真結果如圖7所示。可見，仿真結果在有功功率波動峰值、變化率等方面均具有較高精度。而對于阻抗型調壓井，如果不考慮調壓井的阻抗系數變化，雖然機組有功波動峰值一致，但其動態過程會與實際情況存在較大誤差，如圖7所示。因此對于含阻抗型或其他復雜類型調壓井的水電站，應在仿真模型中詳細計入調壓井的動態特性影響。

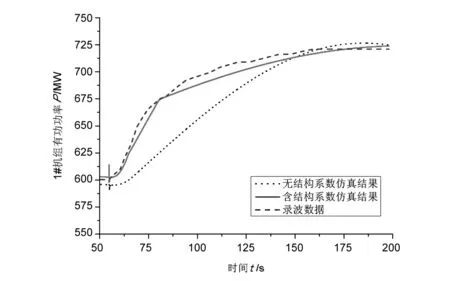
圖7 2號機組安控切機后1號機組有功功率曲線

由于對引水涵洞、分叉壓力鋼管和調壓井時間常數的計算僅利用了部分尺寸參數，因此不可避免與實際錄波曲線存在誤差。但該方法可應用于已知少量水力參數條件下的前期規劃研究和快速建模分析。水電站投產后，通過原動機建模試驗開展對水錘時間常數的實測可有效提高模型的精確度。

5 結 論

(1)針對一管多機長引水系統水電站的動態響應特點，提出適應電力系統中長期穩定分析的水輪機降階模型。

(2)針對水電站調壓井結構復雜、阻抗系數難以確定等特點，提出以調壓井結構系數動態修正調壓井溢流時間常數的方法，提高仿真模型的準確性。

(3)與電網實測擾動數據的對比分析表明，該模型能夠正確反映中長期過程中水電機組的動態響應，可用于此類特殊布置水電站的安全穩定性分析。

[1] 高慧敏，劉憲林，徐政．水輪機詳細模型對電力系統暫態穩定分析結果的影響[J]．電網技術，2005，29(2)：5-9．

[2] 李華，史可琴，范越，等．電力系統穩定計算用水輪機調速器模型結構分析[J].電網技術，2007，31(5)：25-30．

[3] 湯涌，宋新立，劉文焯，等．電力系統全過程動態仿真中的長過程動態模型——電力系統全過程動態仿真軟件開發之三[J]．電網技術，2002，26(11)：20-25．

[4] Working Group on Prime Mover and Energy Supply Models for System Dynamic Performance Studies. Hydraulic Turbine and Turbine Control Models for System Dynamic Studies[J]．Transactions on Power System，1992，7(1)：167-179．

[5] Hannett L.N ，Feltes J.W，Fardanesh B ，et al．Modeling and Control Tuning of a Hydro Station with Units Sharing a Common Penstock Section[J]．IEEE Transactions on Power Systems，1999，14(4)：1407-1414．

[6] 曾云，張立翔，郭亞昆，等．共用管段的水力解耦及非線性水輪機模型[J]．中國電機工程學報，2012，32(14)：103-108．

[7] Kunder P. Power System Stability and Control[M]. New York：McGraw-Hill，1994．

[8] DL/T 5058-1996，水電站調壓室設計規范[S].

[9] 程永光，楊建東．用三維計算流體力學方法計算調壓室阻抗系數[J]．水力學報，2005，36(7)：787-792．

[10] 付亮，王義國．有調壓井水電站甩負荷試驗與仿真分析[J]．水電能源科學，2012，30(6)：154-157．