PO2自由基的光譜常數和非諧力場的理論研究

齊崇海，王美山，楊傳路，徐 強

（魯東大學物理與光電工程學院，煙臺264039）

1 引 言

PO2自由基不僅是磷或其他含磷分子的氣相氧化反應的關鍵中間產物，而且在有機磷混合物的燃燒化學方面扮演著重要角色［1-4］.精確的光譜信息對于理解PO2自由基的結構和化學性質以及對PO2自由基參與的化學反應的監測非常重要.由于PO2自由基是瞬態分子，因此對于它的光譜實驗的精確觀測存在很多困難.然而，PO2自由基的光譜性質研究受到了越來越多的實驗和理論工作者的極大關注［5-15］.在實驗方面，1983年，Verma和McCarthy［5］利用瞬時放電技術首次探測了PO2自由基波長在3115-2680? 之間的光譜.1985年，Kawaguchi等人［6］首次用微波和遠紅外激光磁共振光譜技術測量了PO2自由基基態的100條轉動譜線，通過光譜分析得到了PO2自由基基態（2A1）精確的轉動精細結構和超精細系數.1995年，Qian 等人［7］用二極管激光吸收光譜技術測得并標記了PO2自由基基帶的300多條振轉躍遷譜線，并固定基轉動態系數為更精確的微波或激光磁共振值，通過擬合得到了ν3=1態的光譜常數.2000年，劉煜炎等人［8］通過對氣相PO2自由基的微波譜、激光磁共振和二極管激光光譜的全域分析，得到了一組精確的分子光譜常數.2011 年，Lawson 等人［9］制備了較前人濃度更高的PO2自由基，利用二極管激光吸收光譜技術記錄了PO2自由基ν3態的更多的譜線，通過擬合得到了基態和ν3=1 態的光譜常數.在理論方面，1984 年，Lohr［10］在HF／6-31G＊理論水平上計算了PO2自由基基態X2A1的平衡幾何結構.1989 年，Y.Kabbadj和J.Lielin［11］分別用自洽場和多重組態自洽場方法計算了PO2自由基的基態12A1和幾個低激發態12B2，12A2，12B1，22A1的幾何結構和振動頻率.1995年，Xu等人［12］分別用HF、MP2和CISD 方法計算得到了PO2自由基的平衡幾何結構和振動頻率.1996年，Cai等人［13］在MRD-CI／TZ+2d+R 理論水平上計算了PO2自由基的基態X2A1和其三個低激發態12B212A212B1幾何結構、力常數和振動頻率.2002 年，Lee 等人［14］等人用CIS、CASSCF、MP2、RCCSD 方法計算了PO2自由基的基態和一些低激發態的幾何結構和諧振頻率.2007年，Zhang等人［15］計算了PO2自由基的能量、平衡結構和諧振頻率.2012 年，曾暉和趙俊［16］分別用B3LYP、B3P86、CCSD 和Q-CISD（T）方法以及6-311++G（3df，3pd）和cc-pvTz基組計算了PO2自由基的基態的平衡幾何結構、諧振頻率和能量.綜上所述，關于PO2自由基的研究主要集中在其基態和低激發態的幾何結構、諧振頻率、轉動常數、四次或六次離心畸變常數等光譜常數上，而對于研究PO2自由基精確光譜非常重要的非諧性常數、振轉相互作用常數、科里奧利耦合常數、三次和四次力常數還未見報導.

近年來，隨著計算分子能量二階導數解析方法的發展，使得利用從頭算方法計算小、中型分子的振轉光譜、諧振或非諧振力場成為可能.利用得到的力場，可以確定分子的各種光譜常數，如諧振常數、非諧振修正常數、轉動常數、離心畸變常數等等.非諧振力場的從頭算方法（如CCSD（T）、MP2、CISD、DFT）的研究表明，計算得到的光譜常數與實驗值符合的很好，這意味著用從頭算力場研究分子的光譜性質是可靠的［17-19］.本文分別用 密 度 泛 函 理 論 方 法［20］（B3LYP，B3PW91，B3P86）以及cc-pvQz和6-311++G（3df，3pd）基組計算了PO2自由基的平衡幾何結構、轉動常數、基頻和諧頻、四次和六次離心畸變常數，并與它們相應的實驗或理論數據進行了比較.在此基礎上，預測了該自由基的非諧性常數、振轉相互作用常數、科里奧利耦合常數、三次和四次力常數.

2 計算方法

本文采用的3 種密度泛函理論方法 （在Gaussian03［21］程序下運行）是：B3LYP（Becke型3參數混合交換泛函［22］和Lee-Yang-Parr相關泛函［23］）、B3PW91 （Perdew 和 Wang［21，24-25］在1991年提出的非局域交換-相關泛函及由混合方法組成的Becke型3參數泛函［26］）和B3P86（Perdew 梯度校正并加上其在1981年提出的局域相關泛函）.對于每一種方法，分別考慮了cc-pvQz和6-311++G（3df，3pd）基組.對于cc-pvQZ基組，P原子從初始基組（16s，11p，3d，2f，1g）收縮為（6s，5p，3d，2f，1g）［27］，O 原子從初始基組（12s，6p，3d，2f，1g）收縮為（5s，4p，3d，2f，1g）［27］；對于6-311++G （3df，3pd）基組，P 原子從初始基組（14s，10p，3d，1f）收縮為（7s，6p，3d，1f）［27］，O 原子從初始基組（12s，6p，3d，1f）收縮為（5s，4p，

3d，1f）［27］.

利用解析的能量梯度和C2v對稱性，我們優化了PO2自由基的平衡幾何結構.在得到的平衡幾何結構基礎上，從解析能量梯度出發用解析方法計算了諧振力場.我們用B3PW91、B3LYP 和B3P86 方法計算了三次、四次力常數，利用這些力常數導出了相應的非諧振光譜常數［28，29］.

3 結果與討論

表1-9給出了PO2自由基的平衡幾何結構參數、光譜常數以及各階力常數的計算結果，并將它們與相應的實驗數據進行了比較.需要指出的是，在下列所有表中VQZ表示cc-pvQz基組，G 代表6-311++ G（3df，3pd）基組.

表1列出了我們用密度泛函的方法優化的PO2自由基的平衡幾何結構以及前人的實驗和理論結果.從表中可以看出，B3PW91／G 理論水平計算的P-O 鍵長與實驗值僅差0.0002 ?，而B3P86／G 和B3LYP／G 理論水平下的結果與實驗值分別相差0.0017 ? 和0.0034?.B3PW91／G計算的∠O-P-O 鍵角與實驗值僅相差0.15°，而B3P86／G 和B3LYP／G 給出的誤差分別是0.24°和0.68°.由表中可以看出，上述三種密度泛函方法用VQZ基組計算的結果比用基組G 計算的結果與實驗值的誤差要大些.可見，B3PW91／G 理論水平得到的PO2自由基的平衡幾何結構參數與實驗值吻合得最好.

表1 PO2自由基的平衡幾何結構（鍵角：度；鍵長：埃）Table 1 Molecular geometry structures of PO2free radical（angle in degree，bond length in?）

PO2自由基的平衡態和基態的轉動常數見表2.表2同時給出了基態轉動常數的實驗結果.到目前為止，平衡轉動常數的實驗結果以及平衡態和基態的理論計算都未見報導.基態的轉動常數（A0，B0，C0）是由平衡轉動常數（Ae，Be，Ce）通過考慮振轉耦合微擾［30］得到的.從表中可以看出，用B3PW91／G 和B3P86／G 理論水平與實驗結果［9］的偏差分別在0.0263132cm-1和0.0326347 cm-1內.而B3LYP方法得到的結果比實驗值以及B3PW91和B3P86方法給出的值偏低，但在誤差范圍內也是可接受的.因此，B3PW91／G 給出的結果可以作為該自由基平衡轉動常數的預測值.

表2 PO2自由基的轉動常數（cm-1）Table 2 Rotational constants of PO2free radical（in cm-1）

表3 列出了PO2自由基的諧振頻率和基頻.到目前為止，該自由基基頻的實驗結果和理論計算還未見報導.在計算中，基頻νi可通過公式（1）由相應的諧振頻率ωi和非諧性常數xij得到：

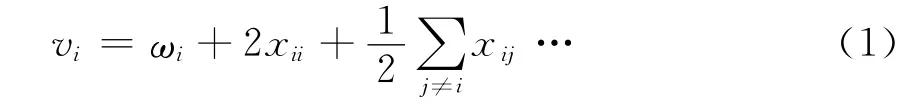
從表3可以發現，B3PW91／G 理論水平計算的ω1與實驗值吻合的很好，而B3P86／G 高估了實驗值，B3LYP／G 低估了實驗值.在本文的計算結果中，三種密度泛函方法和基組G 給出的ω2結果和實驗值的誤差都在13cm-1以內，而以前和我們理論計算的ω3的誤差與實驗值相比稍大，VQZ基組給出的結果比基組G 的好，然而，B3PW91／G 給出的相對誤差是6.33%.

表4不僅列出了我們計算的PO2自由基的平衡四次離心畸變常數，而且也給出了振動基態的實驗數據.從表中我們能夠看出，除了δk以外，B3PW91、B3LYP 和B3P86方法用基組G 計算的結果與實驗值都很接近.對于δk的值，無論我們用何種方法何種基組進行計算，雖然彼此結果都很接近，但與實驗值相差0.51cm-1左右.可見，從平衡態到基態，對四次離心畸變常δk的影響是顯而易見的，而對其它四次離心畸變常數影響較小，甚至忽略不計.

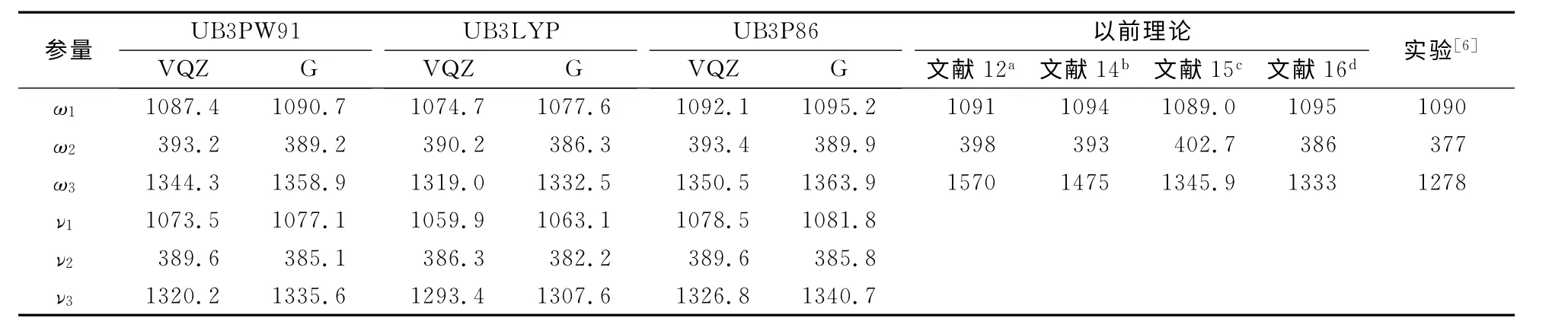
表3 PO2自由基的基頻和諧振頻率（cm-1）Table 3 Harmonic frequencies and fundamental wave numbers ofPO2free radical（in cm-1）

表4 PO2自由基的平衡四次離心畸變常數（cm-1）Table 4 Quartic centrifugal distortion constants ofPO2free radical（in cm-1）

表5列出了我們計算的PO2自由基的平衡六次離心畸變常數，并且給出了該自由基振動基態的實驗數據.從表5容易看出，三種密度泛函給出的各個平衡六次離心畸變常數的數量級和符號是一致的.但是，與已有實驗結果相比誤差非常大.譬如HK，B3PW91／G 理論水平給出的與實驗結果［9］的相對誤差幾乎是100%；HNK的實驗和理論結果符號都是相反的.可見，PO2自由基的平衡六次離心畸變常數和該自由基振動基態的六次離心畸變常數相差很大，它們的誤差不能忽略不計.因此不能用平衡六次離心畸變常數代替振動基態的六次離心畸變常數.

表5 PO2自由基的平衡六次離心畸變常數（cm-1）Table 5 Sextic centrifugal distortion constants ofPO2free radical（in cm-1）

表6給出了B3PW91、B3LYP和B3P86三種密度泛函方法考慮基組VQZ 和G 計算的PO2自由基的非諧性常數xij.到目前為止，實驗和理論上還未見該自由基非諧性常數的相關報導.從表中可以看出，在密度泛函理論方法下計算的結果都相差不大.我們計算的非諧性常數可以作為xij的預測值.

表6 PO2自由基的非諧性常數xij （cm-1）Table 6 Anharmonic constantsxij of PO2free radical（in cm-1）

表7列出了我們計算的PO2自由基的振轉相互作用常數αXi（X=A，B，C；i=1-3），據我們所知，目前還未見該自由基振轉相互作用常數的相關實驗和理論報導.從表中可以看出，我們用B3PW91、B3LYP 和B3P86 方 法 結 合VQZ、G 基組首次得到的振轉相互作用常數具有相同的符號和量級；在一定的誤差范圍內計算的結果作為預測值是可以接受的.

表7 PO2自由基的振轉相互作用常數（cm-1）Table 7 Vibration-rotation interaction constants of PO2 free radical（in cm-1）

表8列出了PO2自由基的科里奧利耦合常數ζij（i=3，j=1-2）.由于科里奧利力的存在，分子整體的轉動對振動產生影響，使得原本相互獨立的振動模式之間發生能量交換，從而影響分子的振轉光譜，特別是對紅外光譜和拉曼光譜行為產生影響.目前還未見PO2自由基的科里奧利耦合常數相關的實驗和理論報導.我們用B3PW91、B3LYP 和B3P86方法以及VQZ和G 基組給出的科里奧利耦合常數在一定誤差范圍內彼此吻合得很好，可以作為該自由基科里奧利耦合常數的預測值.

表8 PO2自由基的科里奧利耦合常數Table 8 Coriolis coupling constants of PO2free radical

表9 列 出 了 我 們 用B3PW91、B3LYP 和B3P86方法下結合VQZ 和G 基組計算的PO2自由基的三次、四次力常數.由定義可知，簡正坐標下二階力常數即為相應的諧振頻率（見表3）.從表3我們知道，我們計算的PO2自由基的二階力常數與實驗值吻合得很好.到目前為止，還沒有PO2自由基三次、四次力常數的相關報導.我們用三種密度泛函方法計算的結果彼此之間接近，因此可以作為PO2自由基的力常數的預測值.

表9 簡正坐標下PO2自由基的三次、四次力常數（cm-1）Table 9 Cubic and quadratic force constants ofPO2free radical in normal coordinates（in cm-1）

4 結 論

我們應用密度泛函方法（B3LYP、B3PW91、B3P86）結合VQZ和G 基組計算了PO2自由基的完全四次力場和各類光譜常數.結果表明：密度泛函方法得到的結果與實驗值在大多數情況下吻合得較好.其中，B3PW91／G 理論水平下計算的結果是相對可靠的，可以作為實驗上還未觀測到的光譜常數的預測值.由本文得到的各類光譜常數代入非對稱約化下的有效轉動哈密頓量表達式（2）就可以計算PO2自由基的轉動能級，這對于精確標識實驗上觀測到的PO2自由基轉動光譜是必不可少的.

在上面公式中，AK=A-（B+C）／2，AJ=（B+C）／2，a=（B-C）／2，［，］+表示對易運算.

［1］ Korobeinichev O P，et al.The destruction chemistry of organophosphorus compounds in flames-I：quantitative determination of final phosphorus-containing species in hydrogen-oxygen flames ［J］.Combust.Flame，1999，118：718.

［2］ Korobeinichev O P，Chernov A A，Bolshova T A.The chemistry of the destruction of organophosphorus compounds in flames-IV：destruction of DIMP in a flame of H2+ O2+ Ar［J］.Combust.Flame，2000，123：412.

［3］ Jayaweera T M，et al.Flame inhibition by phosphorus-containing compounds over a range of equivalence ratios ［J］.Combust.Flame，2005，140：103.

［4］ Werner J H，Cool T A.Kinetic model for the decomposition of DMMP in a hydrogen／oxygen flame［J］.Combust.Flame，1999，117：78.

［5］ Verma R D，McCarthy C F.A new spectrum of the PO2radical［J］.Can.J.Phys.，1983，61：1149.

［6］ Kawaguchi K，Saito S，Hirota E，et al.Far-infrared laser magnetic resonance detection and microwave spectroscopy of the PO2radical［J］.J.Chem.Phys.，1985，82：4893.

［7］ Qian H B，et al.Detection of the infrared laser spectrum of the PO2radical in the gas phase［J］.Chem.Phys.Lett.，1995，235：255.

［8］ Liu Y Y，Liu X Y，Liu H P，et al.Global analysis of spectra of the PO2radical in the gas phase［J］.Chin.Phys.，2000，9：652.

［9］ Michael A L，Kristian J H，Paul B D.Infrared diode laser spectroscopy of theν3fundamental band of the PO2free radical［J］.J.Mol.Spectrosc.，2011，269：61.

［10］ Lohr L L.A theoretical study of the gaseous oxides PO2and PO，their anions，and their role in the combustion of phosphorus and phosphin［J］.J.Phys.Chem.，1984，88：5569.

［11］ Kabbadj Y，Lievin J.Ab initio study of the electronic structure of the PO2radical［J］.Phys.Scr.，1989，40：259.

［12］ Xu C，Beer E de，Neumark D M.Photoelectron spectrocopy of PO2-［J］.J.Chem.Phys.，1996，104：2749.

［13］ Cai Z L，Hirsch G，Buenker R J.Ab initio study of the electronic spectrum of the PO2radical ［J］.Chem.Phys.Lett.，1996，255：350.

［14］ Lee Edmond P F，et al.Ab initio calculations on PO2and anharmonic Franck-Condon simulations of its single-vibrational-level emission spectra［J］.J.Phys.Chem.A，2002，106：10130.

［15］ Zhang X Y，et al.Ab initio calculations and Franck-Condon analysis of photoelectron spectra of PO2-［J］.J.Mol.Struct.，2008，851：40.

［16］ Zeng H，Zhao J.Theoretical study of the structure and analytic potential energy function for the ground state of the PO2 molecule［J］.Chin.Phys.B，2012，21：078202-1.

［17］ Pang W X，et al.Ab initio study of spectroscopic constants and anharmonic force field of74GeCl2［J］.J.Chem.Phys.，2007，126：194301.

［18］ Sun Y T，et al.Ab initio study of spectroscopic constants and anharmonic force field of FCO2radical［J］.J.Mol.Struct.，2010，951：77.

［19］ Guo Y R，et al.Ab initio study of spectroscopic constants and anharmonic force field of AsH2radical

［J］.J.Theor.Comp.Chem.，2011，10：6 849.

［20］ Kohn W，Sham L.Self-consistent equations including exchange and correlation effects ［J］.Phys.Revn A，1965，140：1133.

［21］ Frich M J，Trucks J W，Schlegel H B，et al.Gaussian 03 ［CP］.Pittsburgh：Guassian Inc.，2003.

［22］ Becke A D.Density-functional thermochemistry III.The role of exact exchange［J］.J.Chem.Phys.，1993，98：5648.

［23］ Lee C T，Yang W T，Parr R G.Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density［J］.Phys.Rev.B，1988，37：785.

［24］ Perdew J P，Wang Y，Accurate and simple analytic representation of the electron-gas correlation energy［J］.Phys.Rev.B，1992，45：13244.

［25］ Foresman B，Frich A.Exploring chemistry with electronic structure methods［M］.2nd.Pittsburgh：Guassian Inc.，1996.

［26］ Becke A D.Correlation energy of an inhomogeneous electron gas：A coordinate-space model［J］.J.Chem.Phys.，1988，88：1053.

［27］ Basis sets were obtained from the Extensible Computational Chemistry Environment Basis Set Database V1.2.2.

［28］ Wilson E B，Decius J C，Cross P C.Molecular Vibrations：The Theory of Infrared and Raman Vibrational Spectra［M］，1955.

［29］ Califano S.Vibrational States［R］，1976.

［30］ Clabo D A，et al.A systematic study of molecular vibrational anharmonicity and vibration-rotation interaction by self-consistent-field higher-derivative methods：Asymmetric top molecules ［J］.Chem.Phys.，1988，123：187.