基于對比度的小波圖像融合算法研究

王正林

(91404部隊，河北 秦皇島066001)

1 引言

圖像融合是指綜合來自多個傳感器對同一場景的圖像數據，充分利用彼此間的互補信息，以獲得更精確和全面的描述［1］。基于小波變換的圖像融合方法具有融合效果好的突出特點，已成為圖像融合應用和研究的熱點。基于小波變換的融合算法的步驟為［2］:①將圖像進行小波分解，得到各層各分量對應的小波系數;②選取融合規則，對各系數進行運算選取;③對處理后的系數進行小波逆變換得到融合圖像。在圖像融合算法中，融合規則的選取是至關重要的，它直接影響融合后圖像的質量［3］。目前融合規則可分為兩大類:基于像素的融合規則和基于區域的融合規則。基于像素的融合規則只對指定的單個像素進行運算，不涉及其鄰域，而基于區域的融合規則充分考慮其鄰域內像素的相關性，融合效果更好，應用更多。目前基于區域的融合規則主要有基于區域方差和基于區域能量的融合算法兩種［4］。圖像經小波分解后得到一個低頻子圖像和多個高頻子圖像，低頻子圖像代表了圖像的近似分量，高頻分量代表了圖像的細節分量，現有的融合規則是單獨對低頻分量或高頻分量處理，忽略了高頻與低頻分量之間的聯系，本文利用對比度概念將低頻分量和高頻分量聯系起來，提出一種基于對比度的小波圖像融合算法。仿真實驗結果表明該算法很好地保留了多幅源圖像的有用信息，能取得較好的融合效果。

2 對比度

假設兩幅圖像為 A(x，y)和 B(x，y)，用 (x，y)表示任意像素的坐標，用 gAi(x，y)與 fNA(x，y)，gBi(x，y)與 fNB(x，y)(其中 i=1，2，…，NB)表示原圖像A和B分別經離散小波變換分解后的高頻和低頻子帶系數。原圖像經過圖像變換分解后的高頻子帶系數代表了原圖像的細節信息，細節信息越多，說明清晰度越高。蒲恬［5］等人將對比度概念應用于多傳感器圖像融合之中。圖像對比度C一般定義為:

式中，LP為圖像局部灰度;LB為圖像局部背景灰度(相當于圖像變換后的低頻分量);LH=LP－LB則相當于圖像變換后的高頻分量。考慮到圖像像素之間的相關性，基于傳統的對比度概念，定義圖像中各像素的新的對比度如下:

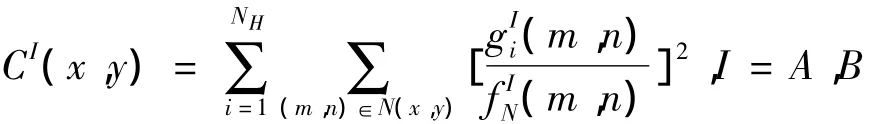
式中，N(x，y)為以像素(x，y)為中心定義的矩形窗口(一般較小，9×9如像素)。CI(x，y)越大，說明原圖像I中像素(x，y)所在局部區域對比度越大，對應像素越清晰。

3 基于對比度的小波融合算法

本文在傳統對比度的基礎上，定義一種新的對比度將高頻分量和低頻分量聯系起來，提出一種基于對比度的小波圖像融合算法。該算法的實現步驟如下:

1)離散小波對兩幅待融合圖像進行小波分解，得到低頻子帶系數和一系列高頻子帶系數;

2)對高頻和低頻子帶系數遍歷計算像素的對比度;

3)對高頻和低頻子帶系數按照相應的融合規則選取融合系數;

4)小波重構得到融合圖像。

圖像分解后的高頻子帶系數代表了細節分量，對比度高的像素是希望得到的像素，故定義高頻子帶的融合規則如下:

其中，gFi(x，y)是融合圖像的高頻系數。

圖像分解后的低頻子帶系數代表了近似分量且位于最高層，常用的融合規則為簡單的像素選擇或

其中，fNF(x，y)是融合圖像的低頻系數。最后通過離散小波重構即可獲得融合圖像。

4 實驗結果

為驗證本文算法的性能，對多聚焦圖像進行融合實驗。圖1和圖2分別為多聚焦圖像，圖1為左聚焦，圖2為右聚焦，圖3為加權平均融合結果，圖4為小波分解后低頻取平均，高頻絕對值選大的結果，圖5為本文算法結果。者加權平均，因本文對比度定義聯系了低頻與高頻子帶系數，所以只需選擇對比度高的像素，即:

圖1 左聚焦圖像

圖2 右聚焦圖像

圖3 加權平均融合結果

圖4 小波分解融合結果

圖5 本文算法融合結果

主觀分析上看，加權平均融合的結果相比原圖像更清晰，但是模糊了原圖像中的清晰部分，對比度降低。采用小波分解算法融合的結果相對加權平均融合的結果較清晰，對比度也得到提升。本文算法的融合結果與小波分解算法的融合結果相似，對比度得到了提升，但是圖4的灰度范圍比圖5的稍大，更符合人眼的視覺特性。

以客觀評價指標標準差和熵［6］，對實驗結果進行評價。標準差和熵可以分別表示為:

其中，^u為圖像像素灰度的平均值;圖像的大小為M×N;P(l)為圖像像素的概率。標準差越大，則灰度級越分散，動態范圍大;熵反映了圖像的平均信息量，熵越大，信息越豐富。三種融合算法結果量化指標如表1所示。

從量化結果上可以看出，本文提出的基于對比度的小波圖像融合算法的結果標準差和熵比加權平均融合算法、小波分解算法都高，說明本文算法的融合結果對比度更高，圖像更清晰，所含信息量更大。

表1 融合效果具體量化指標比較

5 結論

圖像的對比度是圖像質量的一項重要指標，也是復合人眼特性的指標。本文在傳統對比度定義的基礎上定義了一種新的對比度，它將圖像分解后的高頻系數與低頻系數聯系起來。以本文提出的對比度為度量設定融合規則，提出了一種基于對比度的小波圖像融合算法，通過對此算法的實驗仿真分析，圖像融合的效果得到提高。

［1］ JING Zhongliang，XIAO Gang．Image fusion － theory and application［M］．Beijing:Higher Education Press，2007:84 －85．(in Chinese)敬忠良，肖剛．圖像融合——理論與應用［M］．北京:高等教育出版社，2007:84－85．

［2］ TAO Bingjie，WANG Jingru．Image fusion based on relativity of wavelet coefficients computer［J］．Engineering and Applications，2005，25:16 －19．(in Chinese)陶冰潔，王敬儒．采用小波分析的圖像融合方法評述［J］．計算機工程與應用，2005，25:16 －19．

［3］ WANG Xuewei，WANG Shili．Novelmethod of image fusion［J］．Laser ＆ Infrared，2012，42(9):1055 － 1057．(in Chinese)王學偉，王世立．一種圖像融合新方法［J］．激光與紅外，2012，42(9):1055 －1057．

［4］ ZHOU Yunchuan，HEYongqiang，LIJitian．Research on dual－ band target tracking algorithm based on image fusion［J］．Laser＆ Infrared，2011，41(12):1387 －1391．(in Chinese)周云川，何永強，李計添．基于圖像融合的雙波段目標跟蹤算法研究［J］．激光與紅外，2011，41(12):1387－1391．

［5］ PU Tian，FANGQingzhe，NI Guoqiang．Contrast based multi－ resolution image methods［J］．ACTA Electronica Sinica，2000，28(12):116 －118．(in Chinese)蒲恬，方慶喆，倪國強．基于對比度的多分辨率圖像融合［J］．電子學報，2000，28(12):116 －118．

［6］ HU Liangmei，GAO Jun，HE Kefeng．Research on image fusion quality evalution methods［J］．ACTA Electronica Sinica，2004，32(12A):218 －221．(in Chinese)胡良梅，高雋，何柯峰．圖像融合質量評價方法的研究［J］．電子學報，2004，32(12A):218 －221．