Muskingum法的發展及啟示
芮孝芳,張 超
(1.河海大學水文水資源學院,江蘇 南京 210098; 2.河海大學土木與交通學院,江蘇 南京 210098)
據記載,洪水演算問題為Graff于1833年首先提出,但遺憾的是Graff并未給后人留下具體的洪水演算方法[1]。直到20世紀30年代中期,美國陸軍工程師團在修建位于Colorado河的一項水利工程時,才由McCarthy提出了一個至今仍風靡世界的洪水演算方法,因這個方法首先使用在Colorado河支流Muskingum河的洪水演算中,故后人將其命名為Muskingum法[2]。
McCarthy之所以能提出Muskingum法,筆者認為有其必然性,也有其偶然性。水量平衡原理早在17世紀就在水文學中確立,至McCarthy所處的時代已達到了深入人心的地步,但河段水量平衡方程包含了河段下斷面出流量和河段槽蓄量兩個未知項,僅根據河段水量平衡方程顯然是不可能解決洪水演算問題的。McCarthy當時作出了一個假設:如果能找到既能與同時刻河段槽蓄量呈單值關系,又能根據河段上斷面入流量和下斷面出流量確定的“另一個流量”,那么問題就可以迎刃而解。實踐證明,這個假設在一定條件下居然成立。必然性與偶然性相結合就造就了洪水演算的Muskingum法。
Muskingum法的成功引起了水文學家的研究興趣。自20世紀30年代以來,水文學家對Muskingum法的研究主要集中在槽蓄方程的構建和所含參數的物理意義上。這場學術討論,參與度之廣,持續時間之長,在水文學發展史上十分罕見,令人稱奇。
1 經驗解釋時期
經驗解釋時期大體上從1934—1956年,研討的問題主要是對Muskingum法槽蓄方程的理解和確定其中參數的方法。因為這一時期基本上圍繞著McCarthy創建Muskingum法的思路進行研討,所以也可稱為McCarthy-Muskingum法時期。
1.1 對槽蓄方程的理解
McCarthy設想在洪水波運動情況下,河段槽蓄量由“柱蓄”和“楔蓄”兩部分組成(圖1)[2]。“柱蓄”是相應于河段下斷面出流量O的河段槽蓄量,在圖1中形似柱體,因此而得名。“楔蓄”是相應于河段上斷面入流量I與其下斷面出流量O之差的河段槽蓄量,在圖1中形似楔體,因此而得名。McCarthy假設“柱蓄”和“楔蓄”的計算式分別為W柱=KO和W楔=Kx(I-O),其中K為蓄量系數,x為與楔體形狀有關的系數。這樣,河段槽蓄方程就可寫成:
W=K[xI+(1-x)O]
(1)
在式(1)中,[xI+(1-x)O]是以x為I的權重和以1-x為O的權重的河段加權平均流量,是河段上、下斷面流量的線性組合,因為通過選擇x值可能使其與河段槽蓄量呈一一對應的單值關系,所以稱其為示儲流量,用Q′表示。
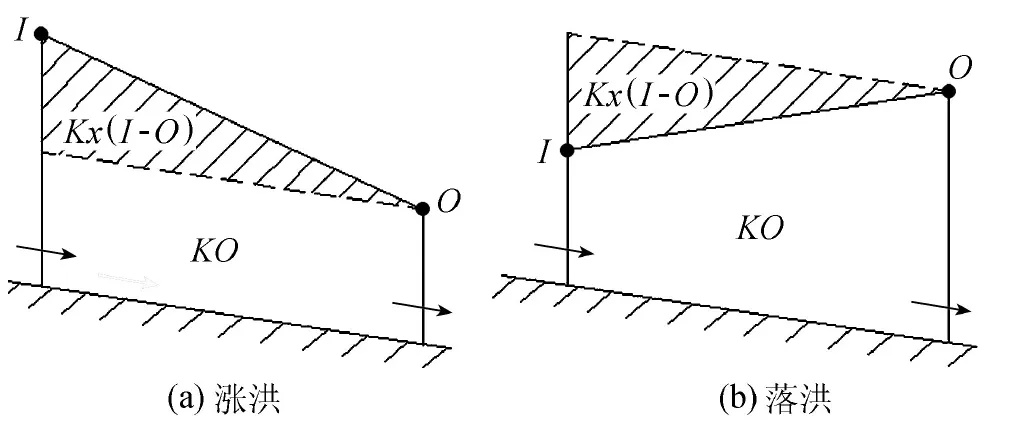
圖1 “柱蓄”和“楔蓄”
Linsley等[3]曾試圖用水力學知識來解釋槽蓄方程,因為槽蓄量W與水位一般具有拋物線型的單值關系。如果假設水位與流量也具有拋物線型的單值關系,那么就可以導得槽蓄量W與流量Q具有下列拋物線型關系:
W=aQm
(2)
式中:a、m分別為經驗系數和指數。
如果分別以河段上斷面入流量I和下斷面出流量O計算河段槽蓄量,那么由式(2)就有:
(3)
Linsley等認為,只要不是洪峰或洪谷處在河段中,河段的槽蓄量W應在WI與WO之間,且W應是WI與WO的加權平均。令權重分別為x和1-x,則有:
W=a[xIm+(1-x)Om]
(4)
對于天然河道,m一般近似為1。在式(4)中,若取m=1,并將a換成K,則結果與式(1)完全相同。
無論是McCarthy的解釋,還是Linsley等的解釋,都認為x是一個權重,其取值可以在0~1之間。但這一時期的大量實踐卻并未發現有x>0.5的情況, “對大多數河流來說,x在0~0.3之間,平均接近于0.2”[3],這是為什么?
1.2 參數確定方法
根據McCarthy構建河段槽蓄方程式(1)的基本思路,只要式(1)成立,就一定可以找到一個x,使示儲流量Q′與河段槽蓄量W呈單值線性關系。這種直觀的想法就導致了確定參數x和K的試錯法[3]。試錯法常常給人以計算繁復之感覺,為避免這一點又提出了圖解分析法和最小二乘法。
圖2為根據河段上、下斷面實測流量資料得到的以河段上斷面入流量I為參變量的河段槽蓄量W與其下斷面出流量O的關系,稱為經驗槽蓄曲線[4],據此確定Muskingum法參數的方法就稱為圖解分析法。事實上,由式(1)容易得到:
(5)
(6)
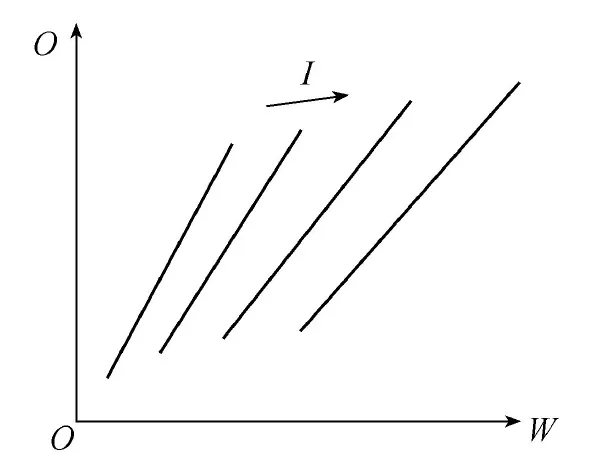
圖2 經驗槽蓄曲線
最小二乘法是一種基于離差平方和最小的思路構建的推求Muskingum法參數的解析法。以由式(1)計算的槽蓄量與由實測資料求得的槽蓄量的離差平方和最小作為擬合準則,以河段水量平衡方程作為約束條件,可得確定x和K的公式[5]分別為
(7)
(8)
式中:Ii、Oi、Wi分別為第i時刻實測的河段上斷面入流量、下斷面出流量和相應的槽蓄量;n為時段數。
上述確定Muskingum法參數的方法對實測資料的依賴性很強,這就會產生一個問題:由于在暴雨洪水期間,河段的區間入流一般是不可避免的,因此,它必將作為一種外因對河道洪水波運動規律起著干擾作用,如果對此處理不合理,那么就無法得出合理的x和K。對圖3(圖中W使用的單位是行業通用單位)所示的Q′-W關系[6],之所以無論x取何值,Q′-W都不可能趨于單值關系,就是因為區間入流難以合理處理。實踐證明,區間入流比重越大,這種情況就越易出現。如果區間入流可全部實測,這種情況一般就不會出現了。

圖3 沅陵—王家河河段1970年9月一次洪水的Q′-W關系
2 特征河長解釋時期
特征河長解釋時期大體從1957—1967年,研究的問題主要是建立水文學的槽蓄理論和揭示Muskingum法參數與特征河長的關系。因為這一時期主要是圍繞著Kalinin和Milyukov創建的特征河長的基本理論進行的,所以也可稱為Kalinin-Muskingum法時期。
2.1 中國的實踐
20世紀50—60年代,中國水文科學家和工程師在使用Muskingum法的大量實踐中發現[7]:①同一條河流,在河段長大致相同的情況下,上游河段的x一般比下游河段的x大。例如西江南寧—橫縣河段,河段長163 km,得x=0.30;而位于其下游的梧州—高要河段,河段長160 km,得x=0.05。②河底比降相同的河段,長河段的x大于短河段的x。例如松花江佳木斯—富錦河段,河段長191 km,河底比降1/10 000,得x=0.35;贛江吉安—峽江河段,河段長66 km,河底比降1/10 000,得x=0.25。③河段長相同,河底比降大的x大于河底比降小的x。例如永定河青白口—三家店河段,河段長53 km,河底比降31.9/10 000,得x=0.49;新沂河障山—沐陽河段,河段長50 km,河底比降2.5/10 000,得x=0.45。④有大支流匯入的河段,x一般都比較小。例如錢塘江羅桐埠—蘆茨埠河段,河段長51 km,河底比降0.25/10 000,河段中間有大支流匯入,得x=0;伊洛河龍門—黑石蘭河段,河段長57 km,河底比降0.3/10 000,河段中有大支流匯入,得x=0.10。⑤有些河段,x必須為負。例如長江萬縣—宜昌河段,河段長318 km,河底比降2.7/10 000,在三峽建庫前x=-0.60。
上述中國水文學家和工程師在實踐中發現的問題,顯然無法從McCarthy和Linsley等對Muskingum法的經驗解釋中尋找到答案。
2.2 x與特征河長的關系
正當人們感到“山重水復疑無路”的時候,是Kalinin和Milyukov[8]發現的“特征河長”撥開了迷霧,又在人們眼前出現了“柳暗花明又一村”的美景。1958年Kalinin和Milyukov利用水力學知識導出了如下特征河長l的表達式:
(9)
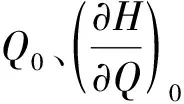
筆者認為,特征河長的發現對水文學有多方面的重要意義,其中所開創的構建槽蓄方程的理論途徑最值得稱道。根據特征河長的物理意義,如果河段長L正好等于特征河長l,則河段槽蓄量W與特征河段出流量Ol呈單值函數關系,而且在多數情況下,可將此單值函數關系視作如下近似線性函數關系:
W=KlOl
(10)
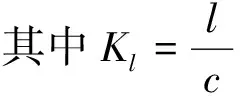
式中:Kl為洪水波在特征河長內的傳播時間;c為洪水波速。
由于Muskingum法的示儲流量Q′也與河段槽蓄量呈單值線性關系,因此,只要找到使Q′=Ol的條件,就可對Muskingum法作出一定的物理解釋。水文學家從不同的角度證明這個條件[4,7]就是:
(11)
式中:L為河段長。
由式(11)可知:①對一定的河段長L,當i0→∞時,由于l→0,因此x=0.5;當i0→0時,由于l→∞,因此,x<0;當i0在0~∞之間時,由于l在∞~0之間,所以x≤0.5。②對不同的L與l關系,若L>l,則x在0~0.5之間;若L=l,則x=0;若L 圖4 1968年8月洪水王家河站計算與實測流量過程線 (12) 其中A=C1+C0C2 C0+C1+C2=1 筆者曾使用Z-變換和留數定理對連續演算Muskingum法的匯流系數做了推導,得到了與上述相同的結論[7]。 水力學解釋時期大體上從1967年至今。河道洪水波運動在水力學上屬于緩變不恒定流運動,描寫其運動規律的方程式早在1871年就由St.Venant導出,后人稱之為St.Venant方程組。所謂Muskingum法的水力學解釋就是揭示Muskingum法與St.Venant方程組的關系,開此先河者為Dooge,但為此作出關鍵貢獻的是Cunge。所以這一時期也可稱為Cunge-Muskingum法時期。 1967年,Dooge[12]通過比較線性化的完全St.Venant方程組的響應函數和Muskingum法的響應函數的各階累積量,得到了Muskingum法參數x、K和特征河長l的表達式分別為 (13) (14) (15) Dooge根據完全St.Venant方程組線性化形式也導出與式(11)完全相同的結果,這無疑是對Kalinin和Milyukov結論的有力支持,但卻帶來了一個新問題:為什么在Dooge的推導中,無論特征河長l,還是Muskingum法參數x均與表征流態的弗勞德數有關?為什么當流態為F0>2的急變流時,x、l均出現不合理,以致Muskingum法已不再適用了? 1969年,Cunge[13]發表了一篇題為“關于洪水傳播計算方法(Muskingum法)問題”的著名論文,報道了他在使用四點帶權顯式差分格式推求運動波方程數值解時的有趣發現:如果解的一階截斷誤差正好等于擴散波的擴散系數,那么所得到的運動波方程式的差分解不僅具有與McCarthy-Muskingum法完全相同的演算公式形式和完全相同的演算系數的表達式,而且還變成了擴散波方程的二階精度差分解,條件僅僅是要求滿足: (16) 式中:D為擴散波的擴散系數;c為波速;Δx為河段長。 筆者[9,14]曾導得特征河長l與擴散系數D的關系為 (17) 將式(17)代入式(16)得到的x表達式也與式(11)完全相同。 Cunge雖然利用運動波方程的四點帶權顯式差分格式數值解的一階截斷誤差等于擴散波擴散系數這一條件,給出了Muskingum法參數x的物理意義,揭示了Muskingum法演算公式就是擴散波方程具有二階精度的差分解,但是沒有給出Muskingum法演算公式作為擴散波方程式顯式差分格式解的穩定性條件。 1978年,Koussis[15]針對常微分方程形式的河段水量平衡方程和Muskingum法槽蓄方程式(1),通過Taylor級數展開,導出了下列偏微分方程: (18) 式中:Q為傳播流量;c為波速;x為Muskingum法參數;Δx為河段長。 在式(18)中,若令 (19) 式中D為擴散波的擴散系數,則有 (20) 式(20)即為擴散波方程式。這就表明,Kousis的研究結論是河段水量平衡方程與Muskingum法槽蓄方程,在滿足條件式(19)的情況下,就是描寫擴散波運動的擴散波方程。考慮到式(17),條件式(19)與式(11)完全相同。 Cunge和Kousis從正與反兩種角度證明了只要條件式(11)滿足,Muskingum法演算公式就是擴散波方程式的二階精度數值解,河段水量平衡方程和Muskingum法槽蓄方程描述的就是擴散波運動。 由數值分析理論知,只有具有計算穩定性的差分格式才有意義,否則就會因截斷誤差在傳遞過程中的放大或震蕩,造成所描寫的現象的物理圖景不合理的后果。隱式差分格式是無條件穩定的,但顯式差分格式卻是條件性穩定的。Muskingum法的演算公式作為擴散波方程的顯式差分解的穩定性條件是什么呢? 2008年,筆者[16]曾應用Ven Neumamm理論對Muskingum法的數值穩定性進行分析,得到的穩定性條件為 x≤0.5 (21) 聯系到曾經對式(11)所作的分析,x≤0.5不僅是Muskingum法物理意義上的要求,而且是數值解穩定性的條件。 a. 如果說St.Venant方程組的問世開創了用水力學理論探索河道洪水波運動的途徑,那么Muskingum法的出現便開始了用水文學理論研究河道洪水波運動的途徑。經過近一個世紀的發展,不僅找到了這兩條途徑的共同點,也明確了它們的不同點。適用于運動波和擴散波的洪水演算是它們的共同點,是否適用動力波的洪水演算是它們的不同點。 b. 筆者認為在近百年中,Muskingum法的發展已經歷了3個時期,即經驗解釋時期、特征河長解釋時期和水力學解釋時期。在經驗解釋時期,論及的中心議題是槽蓄方程的構建和示儲流量的實質。在特征河長解釋時期,論及的中心議題是Muskingum法與特征河長的關系,以及用Muskingum法進行洪水演算時初始階段出現不合理現象的原因。在水力學解釋時期,論及的中心議題是Muskingum法的水力學基礎和Muskingum法計算結果物理上合理、數值上穩定的條件。Muskingum法的理論和應用價值就是在這樣的發展過程中得到了不斷的提升。 c. Muskingum法的槽蓄方程,原本是一個經驗假設,但在世界上許多河流的洪水演算中取得了令人滿意的精度。一個經驗性的假設為什么能屢屢得到應驗呢?是不是這個假設實質上已是人們不自覺地揭示了洪水波運動的本質了呢?如果是這樣,那么這種洪水波該是什么樣的洪水波呢?現在水文學家終于交出了一份很好的答卷。這一事件表明,在科學研究中,“經驗”不一定永遠是經驗,有些“經驗”,尤其是那些似乎“放之四海而皆準”的經驗,終有一天會上升到“理論”的。從這個意義上說,“經驗”與“理論”之間并不存在一條不可逾越的鴻溝。在這種由“經驗”向“理論”的升華過程中,科學家的正確思維方法、持之以恒的探索精神、百折不撓的學術批判是十分重要的。 d. 重要的科學發現經常是從某種“假設”開始的,但是在當今的教科書中,總是將一些重要的定理和定律整理“提煉”得有條不紊,好像它們生來有之。這樣,久而久之,學生們就習慣于 “經驗性”的永遠是經驗性的、“理論性”的永遠是理論性的思維方式,而對于在科學探索中發生的實際思維過程卻反而不知甚至不能理解。事實上,在科學史上起引領作用的定律曾經就是一種猜想。就是在今天,科學上仍然充滿了猜想。沒有“猜想”就難以有“創新”。 e. 學習任何知識均應將精力放在正確理解其精神實質上,要牢牢掌握其精髓,而不應采用功利主義的態度,浮在表面就開始做“創新”的美夢。君不見,有文獻曾經將計算與實測流量的離差平方和最小作為目標函數,用最優化方法直接率定Muskingum法的演算系數C0、C1和C2,或者再增加一個水量平衡約束,即C0+C1+C2=1來率定C0、C1和C2。更有甚者,竟將計算與實測水位的離差平方和最小作為目標函數來率定C0、C1和C2。所有這些做法,由于不能保證Muskingum法中x的物理意義,故均不能稱為對Muskingum法的改進和發展。相反,這是一種將原本物理概念清楚的方法胡亂地變成“黑箱子”方法的典型事例。科學研究的目的是盡可能將“黑箱子”變“灰”、變“白”,而不能將“白箱子”變“灰”、變“黑”。 f. Muskingum法的參數x和特征河長l與弗勞德數存在關系,表明了它們與流態有關。由式(13)和式(14)可知,當流態為F0>2的急變流時,出現了x>0.5和l<0的不合理現象,這是為什么?既然Muskingum法的演算公式是擴散波方程具有二階精度的四點帶權顯式差分格式的數值解,為什么只能通過運動波方程才能得到,直接利用差分格式求解擴散波方程卻不能得到?筆者認為這些也許是必須進一步深入研究的問題。若通過物理實驗方法來揭示Muskingum法的物理基礎和適用條件,則將更有意義。 參考文獻: [1] VIESSMEN W, KNAPP J W, GARY L L,et al.Introduction to hydrology[M].New York: Harper & Pow, 1977. [2] CHOW V T.Handbook of applied hydrology[M].New York: McGraw-Hill, 1964. [3] LINSLEY R K, KOHLER M A, PAULHUS J L H.Hydrology for engineers[M].3rd ed.New York: McGraw-Hill, 1988. [4] 華東水利學院水文系.水文預報[M].北京:中國工業出版社,1962. [5] 鐘樂暉.用數解法推求馬斯京根洪水演算法中X和K的數值[J].水利學報,1963(2):43-45.(ZHONG Lehui.The calculation of parametersXandKof Muskingum flood routing method with numerical method[J].Journal of Hydraulic Engineering,1963(2):43-45.(in Chinese) [6] 華東水利學院.中國濕潤地區洪水預報方法[M].北京:水利電力出版社, 1978. [7] 芮孝芳.Muskingum法及其分段連續演算的若干理論探討[J].水科學進展,2002,13(6):682-688.(RUI Xiaofang.Some theoretical studies on the Muskingum method and its successive routing in subreaches[J].Advances in Water Science,2002,13(6):682-688.(in Chinese) [8] KALININ G P,MILYUKOV P I.Approximate computation of unsteady flow[R].Leningrad:Trudy C.I.P.,1958.(in Russian). [9] 芮孝芳.水文學原理[M].北京:高等教育出版社, 2013. [10] 趙人俊.流域匯流計算方法[J].水利學報,1962(2):1-9.(ZHAO Renjun.Watershed concentration calculation method[J].Journal of Hydraulic Engineering,1962(2):1-9.(in Chinese) [11] 趙人俊.流域水文模擬[M].北京:水利電力出版社, 1984. [12] DOOGE J C I.Linear theory of hydrologic systems[M].Washington,D.C.:USDA,1973. [13] CUNGE J A.On the subject of a flood propagation method:Muskingum method[J].Journal of Hydraulic Research,1969, 7(2):1087-1101. [14] 芮孝芳.運動波數值擴散與洪水演算方法[J].水利學報,1987(2):37-43.(RUI Xiaofang.Numerical dispersion of kinematic wave and flood routing method[J].Journal of Hydraulic Engineering,1987(2):37-43.(in Chinese) [15] KOUSSIS A D.Theortical estimations of flood routing parameters[J].Journal of the Hydraulics Division,ASCE,1978, 104(HY1):109-115. [16] RUI Xiaofang,LIU Fanggui,YU Mei.Discussion of Muskingum method parameter X[J].Water Science and Engineering,2008, 1(3):16-23.2.3 連續演算的Muskingum法
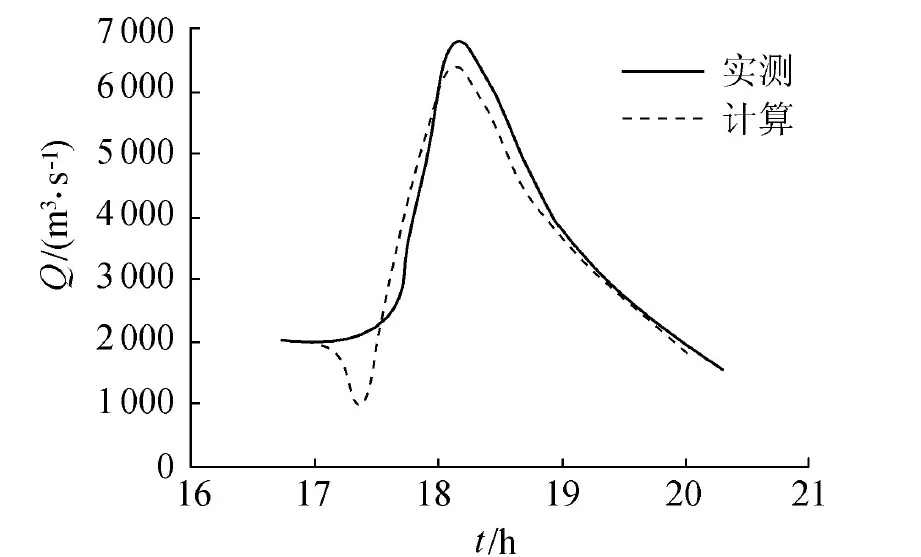
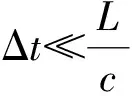
3 水力學解釋時期
3.1 Dooge的研究
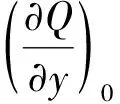
3.2 Cunge的研究
3.3 Koussis的研究
3.4 筆者的研究
4 結論與啟示

