基于重整化群方法的三棱柱單元整體破壞概率模型

顧培英,鄧 昌,湯 雷

(1.南京水利科學研究院材料結構研究所,江蘇 南京 210029; 2.水利部水科學與水工程重點實驗室,江蘇 南京 210029)

目前,許多混凝土結構承擔著生命線工程的重任,其失事所造成的直接、間接經濟損失不可估量。我國很多混凝土結構已進入中老年期,往往存在各種損傷與病害。此外,若混凝土結構遭受地震及其他意外事故,局部破壞在所難免,那么局部破壞對整體安全性的影響以及是否會導致整體倒塌等破壞是目前還無法準確回答的問題，所以有必要開展水工混凝土結構整體安全性研究。

混凝土結構損傷狀況一般是通過外觀破損調查,并借助于多種無損或局部有損專項檢測技術來獲得,但從某種意義上講僅依據局部檢測結果還難以真正達到整體安全性評價的目的。顧培英等[1]提出了一種基于重整化群理論的混凝土結構整體安全性評價新方法。重整化群方法是美國威爾遜在量子場理論中提出來的,他把量子場論中的重整化群方法應用于臨界現象研究,提出重整化群在不動點附近的性質決定了體系的臨界行為,建立了相變臨界現象理論,這是臨界現象研究領域的重大突破,1982年威爾遜也因此獲得諾貝爾物理學獎[2-4]。相變基本特點是系統變量連續變化會造成系統宏觀參數的不連續變化(突變)。重整化群方法可處理各種相變和臨界點問題,其利用了標度不變性,先在最小標度上研究較為簡單的相互作用系統,然后將問題重整化,進一步在大的標度下利用同樣系統研究大的相互作用系統,過程不斷重復[5]。重整化群方法主要有3個方面的應用:①多孔介質中的滲流;②巖石破碎;③斷層破裂。

重整化群方法成功地解釋了各種相變和臨界點問題,得到尺度越來越大情況下的原胞破壞概率遞推公式,建立的是局部與整體的關系,該方法已在巖石破碎和斷層破裂等方面得到應用[6-16]。由于混凝土與巖石均屬脆性材料,性能較為相似,所以可以將重整化群方法“嫁接”到混凝土結構。顧培英等[17]建立了基于小單元、大單元試驗結果的混凝土局部損傷概率確定方法,并針對數值仿真成果,提出混凝土局部損傷概率服從二參數的Weibull分布。顧培英等[1]還針對正方體的水工混凝土結構,建立了不等局部損傷概率與整體安全性之間的關系,但一般水工混凝土結構不具備正方體的條件,經常包含斜面或曲面,需分別對結構體和單元體進行處理,建立符合實際水工混凝土結構的整體破壞概率數學模型。

重整化群方法處理大體積塊體結構具有優越性,適宜應用于重力壩的整體安全性評價。重力壩基本剖面呈三角形,為適應地基變形、溫度變化和混凝土的澆筑能力,用橫縫將壩體分隔成若干個獨立工作壩段。可將每個壩段作為一個整體加以分析,壩段呈三棱柱體結構,所以需推導三棱柱單元的混凝土結構整體破壞概率,其他斜面或曲面結構可通過等效、補償處理,綜合利用三棱柱單元和正方體單元數學模型得到整體破壞概率。本文在基于正方體單元巖石破碎概率模型的基礎上,推導基于三棱柱單元的結構整體破壞概率模型,得到導致結構整體破壞的單元破壞概率臨界值,并對實際工程的原胞級數取值進行分析。

1 正方體單元巖石破碎概率模型

根據文獻[1,5],正方體單元巖石破碎情況如圖1所示。圖1中破碎單元用正方體角上的黑點表示,a、b、c、d、e、f分別為某破碎單元數不變情況下的不同組合形式,數字為破碎單元個數,括號內的數字表示出現該破碎情況的次數。圖1(n)(q)(s)(t)(u)(v)是6種巖石整體破碎情況。

圖1所示的模型假定8個單元的破碎概率相等,用p0表示,分別得出6種情況下各自的破碎概率，并求和， 6種巖石破碎情況下1級原胞破碎概率p1與1級單元破損概率p0之間存在以下關系[1,5]:

(1)

重整化后,可以將同樣的方法應用于更高級原胞,將式(1)中的下標1、0替換成n+1、n,有

(2)

如果1級原胞特征長度為2h,則第n級原胞的特征長度為2nh。

圖1 正方體單元巖石破碎情況示意圖

2 三棱柱單元混凝土整體破壞概率模型

2.1 公式推導

圖2為三棱柱單元混凝土3級原胞三維模型示意圖。與正方體單元巖石破碎假設類似[1,5],原胞中每個單元要么破碎,要么完整,如果原胞兩面之間有一不破壞的“支柱”相連,則認為原胞是完整的。此模型也是8個單元組成1級原胞，每個原胞破壞狀況也有256種情況,去掉重復情況,從拓撲學角度共有36種不同情況,三棱柱單元混凝土破壞情況如圖3所示(編號含義同圖2)。圖3(F)(H)(I)(J)是4種原胞破壞情況。圖4為6c6和6d6三棱柱單元混凝土原胞示意圖,圖4中空白部分表示破壞單元,陰影部分表示完整單元。6c6具有用陰影部分表示的非破壞“支柱”,因而認為是完整的,而6d6任兩個面之間沒有由完整單元組成的“支柱”支撐,是一個破壞原胞。

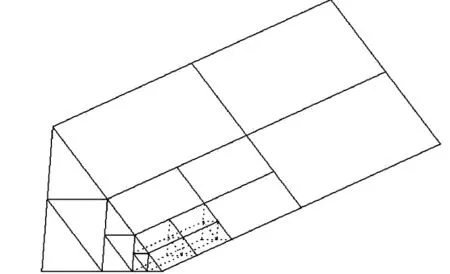
圖2 三棱柱單元混凝土3級原胞三維模型示意圖

圖3 三棱柱單元混凝土破壞情況示意圖

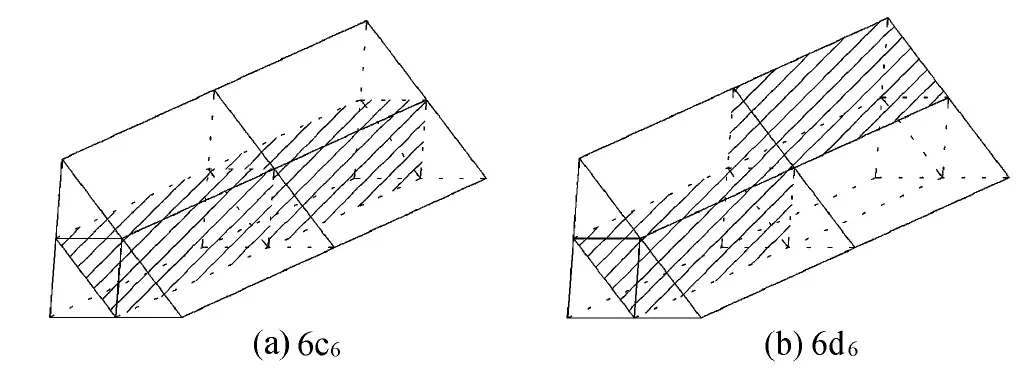
圖4 6c6和6d6三棱柱單元混凝土原胞示意圖

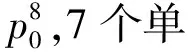
(3)

重整化后,可以將同樣的方法應用于更高級數,將式(3)中的下標1、0替換成n+1、n,有

(4)

2.2 不動點分析

圖5為基于三棱柱單元混凝土整體破壞概率模型pn+1與pn的關系曲線。為了研究不動點,將式(4)改寫成

f(x)=x6(5x2-16x+12)

(5)

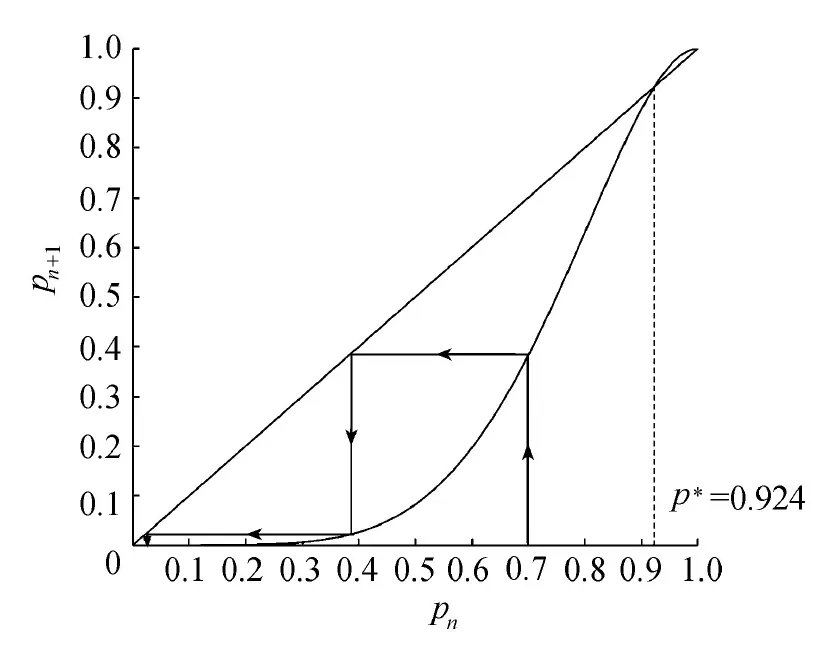
圖5 基于三棱柱單元混凝土整體破壞概率模型pn+1與pn的關系曲線

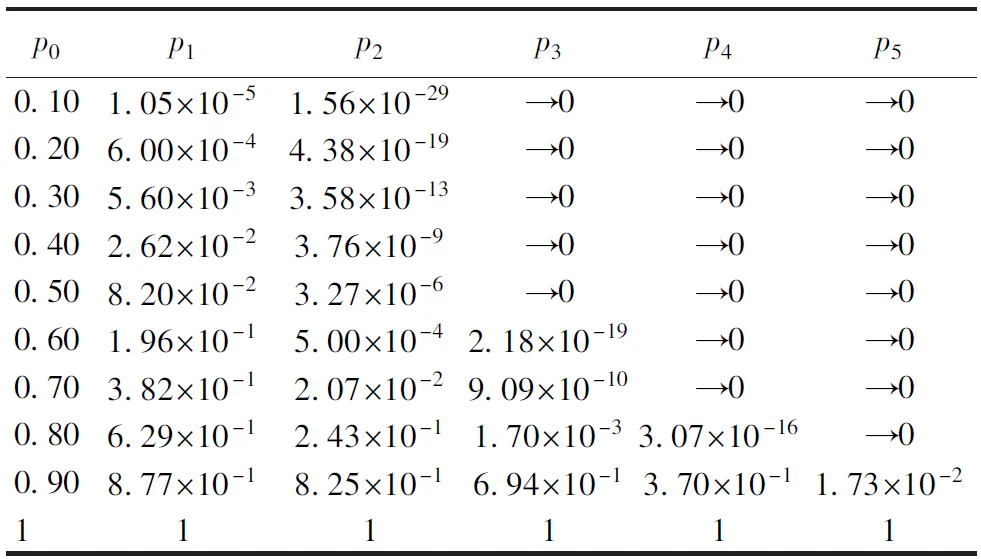
令f(x)=x,可得到不動點。在0

為說明式(4)的迭代過程,考慮一特定情況：當p0=0.70時,由圖5可得p1=0.382 4、p2=0.020 7、p3=9.18×10-10,p3接近零,當迭代繼續下去時,p∞=0,因此,p0=0.70時不會發生整體破壞。當p0=0.95時,p1=0.964 8、p2=0.981 9、p3=0.995 0,p3→1。p*=0.924是一個臨界點,它對應于混凝土發生突變式的破壞。所以,對于小于臨界值的概率,即0

3 原胞級數取值討論

若最大級原胞對應于某一有限的三棱柱混凝土結構體,每個單元破壞概率相等且已知,則可通過式(4)遞推得到該結構整體破壞概率。理論上講,原胞級數趨于無窮大,即1級單元尺度遠小于最大級原胞尺度時,若單元破壞概率不是臨界值p*,則整體破壞概率只有0、1兩種可能,即要么破壞、要么完整。但在實際工程應用中,原胞級數不可能取很大,下面對迭代次數進行進一步的分析。表1為三棱柱單元混凝土結構前5次迭代整體破壞概率計算結果。

表1 三棱柱單元混凝土結構前5次迭代整體破壞概率計算結果

由表1可知,當單元破壞概率p0≤0.70時,2次迭代后p2→0;當p0=0.80時,3次迭代后p3→0;當p0=0.90時,3次迭代后p3=0.694 4,5次迭代后p5→0。所以,大多數情況下,只需3次迭代即可獲得趨于零的整體破壞概率,這時結構完整,隨著p0的增大,收斂速度有所降低;若p0接近于臨界值p*時,3次迭代后p3仍較大,利用收斂速度可判斷接近臨界值的程度。因此,原胞級數即迭代次數取3即可滿足實際工程需要。此外,若迭代后整體破壞概率增大或等于1,則混凝土整體發生破壞。

4 結 語

傳統重整化群方法只能處理正方體巖石破碎問題,但一般水工混凝土結構不具備正方體條件,本文提出并建立了基于重整化群方法的三棱柱單元混凝土結構整體破壞概率模型。通過不動點計算分析,得到導致結構整體破壞的單元破壞概率臨界值。

迭代計算結果表明,大多數情況下,只需3次迭代即可獲得趨于零的整體破壞概率,這說明雖然存在局部破壞,但結構整體是安全的。隨著單元破壞概率的增大,整體破壞概率收斂速度有所降低。若3次迭代后整體破壞概率仍較大,則說明單元破壞概率接近臨界值。若迭代后整體破壞概率增大或等于1,則混凝土整體發生破壞。因此,原胞級數即迭代次數取3可滿足實際工程需要。

本文所提出的概率模型適用于重力壩,在確定外載作用下,其局部破壞相應確定,建立了局部破壞概率與整體安全性之間的關系,此模型可從定量的角度評價混凝土重力壩的整體安全性；其他斜面或曲面結構可通過等效、補償處理,綜合利用三棱柱單元、正方體單元概率模型獲得結構整體破壞概率。值得一提的是,本文模型是基于等概率三棱柱單元,仍有一些問題有待完善,不等概率三棱柱單元的數學模型推導及其分析成果將另文發表,下一步還將研究外力及其他環境因素對結構整體破壞概率的影響規律。

參考文獻：

[1] 顧培英,鄧昌,湯雷.基于重整化群的水工混凝土結構整體破壞概率研究[J].水利水運工程學報,2010(4):1-5.(GU Peiying,DENG Chang,TANG Lei.Damaged probability of concrete for hydraulic structure based on renormalization group theory[J].Hydro-Science and Engineering,2010(4):1-5.(in Chinese)

[2] 于淥,郝柏林.相變和臨界現象[M].北京:科學出版社,1984.

[3] 陳顒,陳凌.分形幾何學[M].北京:地震出版社,2005.

[4] 閻貴卿,閻毅.近代數學物理理論計算與可視化技術[M].長沙:國防科技大學出版社,2000.

[5] TURCOTTE D L.分形與混沌：在地質學和地球物理學中的應用[M].陳顒,鄭捷,季穎,譯.北京:地震出版社,1993.

[6] SAMMIS C G.Non-linear fracture mechanics model for spallation and coupling of nuclear explosions detonated in hard rock[R].Los Angeles:University of Southern California,1998.

[7] LEI Xinglin,NISHIZAWA O,MOURA A,et al.Hierarchical fracture process in brittle rocks by means of high-speed monitoring of ae hypocenter[J].Journal of Acoustic Emission,2005,23:102-122.

[8] CHIAIA B,BORRIBRUNETTO M.Multiscale modelling of stick-slip transition of rough (fractal) surfaces[C]//5th International Conference on Processing & Manufacturing of Advanced Materials.Vancouver,Canada:Materials Science Forum,2007:2594-2600.

[9] BORRIBRUNETTO M,CARPINTERI A,CHIAIA B.The effect of scale and criticality in rock slope stability[J].Rock Mechanics and Rock Engineering,2004,37(2):117-126.

[10] DAVID W F,SCOTT R P.Contamination of silicic magmas and fractal fragmentation of xenoliths in Paleocene plutons on Kodiak Island,Alaska[J].The Canadian Mineralogist,2007,45(1):107-129.

[11] WANG Lianguo,WU Yu,MIAO Xiexing,et al.Mechanism of water-inrush from fault induced by mining near the working face[J].Journal of Coal Science & Engineering (China),2007,13(4):393-395.

[12] SAHIMI M,REZA R T M,BAHRAMINASAB A,et al.Propagation and localization of acoustic and elastic waves in heterogeneous materials:renormalization group analysis and numerical simulations[J].Acta Mechanica,2009,205(1):197-222.

[13] BAHRAMINASAB A,MEHDI V A S,SHAHBAZI F,et al.Renormalization group analysis and numerical simulation of propagation and localization of acoustic waves in heterogeneous media[J].Physical Review B:Condensed Matter and Materials Physics,2007,75(6):1-13.

[14] 高召寧,姚令侃,徐光興.巖石破壞過程的自組織特征與臨界條件研究[J].四川大學學報:工程科學版,2009,41(2):91-95.(GAO Zhaoning,YAO Lingkan,XU Guangxin.Study on self-organized characteristics and criticality condition in the course of rock failure[J].Journal of Sichuan University:Engineering Science edition,2009,41(2):91-95.(in Chinese)

[15] 吳國雄,丁王飛,張洋,等.瀝青混凝土路面開裂破壞的滲流模型分析[J].重慶交通大學學報:自然科學版,2009,28(6):1016-1020.(WU Guoxiong,DING Wangfei,ZHANG Yang,et al.Percolation model of asphalt concrete pavement crack damage[J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(6):1016-1020.(in Chinese)

[17] GU Peiying,DENG Chang,TANG Lei.Determination of local damage probability in concrete structure[C]//2012 International Conference on Modern Hydraulic Engineering.Nanjing,China:China Association of Hydraulic Engineering Education,2012:489-493.