高階差分的值分布

俞偉鵬， 葉亞盛

（上海理工大學理學院，上海 200093）

使用值分布理論的基本概念和標準符號，參見文獻［1］和文獻［2］.設f（z）和α（z）是兩個亞純函數，稱α（z）是f（z）的小函數，如果T（r，α）＝S（r，f），其中當r→∞時，S（r，f）＝o（T（r，f）），除去一個有限對數測度集.

在差分理論中，將f′（z）差分模擬定義為Δcf（z）＝f（z＋c）－f（z），以及Δf（z）＝f（qz＋c）－f（z），其中對于f（k）（z）的差分模擬，定義為以及Δkf（z）＝Δk－1（Δf（z））.經過簡單的計算，有

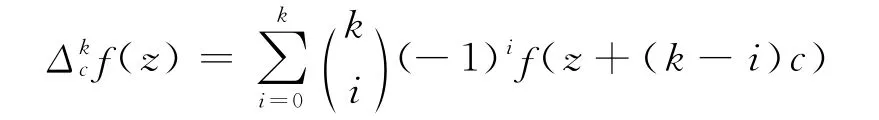
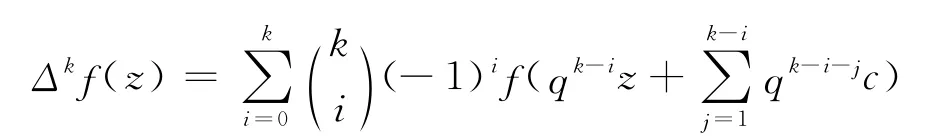
Hayman［3］提出了如下猜想：

上述猜想逐漸得到了證明，Hayman［1］證明了n≥3的情形，Mues［4］證明n＝2的情形，Bergweiler等［5］證明了n＝1的情形.

Hayman［3］也證明了如下結論：

定理2 設n（≥5）為正整數，a（≠0），b為兩個有窮復數，f為復平面上的亞純函數，如果f′－afn≠b，則f恒為常數.

最近，國內外很多文章聚焦于復域上的差分方程和Nevanlinna理論的差分模擬［6－11］，并且得到許多相關的結論.張繼龍等［12］考慮了定理1的高階差分對應，證明了如下定理：

首先改進了定理3：

利用差分的思想，考慮了定理2的高階差分模擬.

還研究了一個高階差分的唯一性定理：

1 引 理

為了證明本文的結論，需要如下幾個引理：

引理1［13］設f是有窮級（記為ρ）超越亞純函數，c∈＼｛0｝，則對于每個ε＞0，有

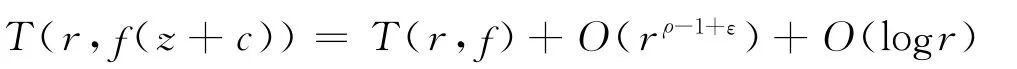
引理2［14］設f是非常數零級超越亞純函數，q∈＼｛0｝，則

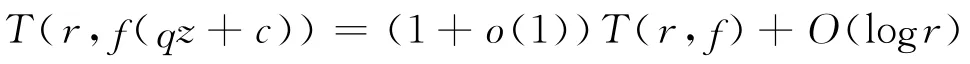
在下對數測度為1的集合上成立.

引理3［14］設f是非常數零級超越亞純函數，q∈＼｛0｝，則

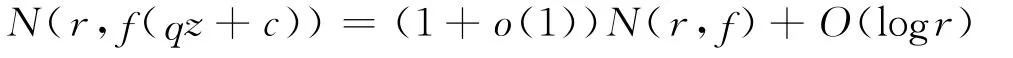
在下對數測度為1的集合上成立.

引理4［6］設f是復平面上的有窮級亞純函數，c∈＼｛0｝，n∈N，則對于f的任意小函數a（z），有對所有的r成立，除去一個有限對數測度集.

引理5［1］設f是復平面上的亞純函數，a1（z），a2（z），a3（z）是f（z）的3個小函數，則

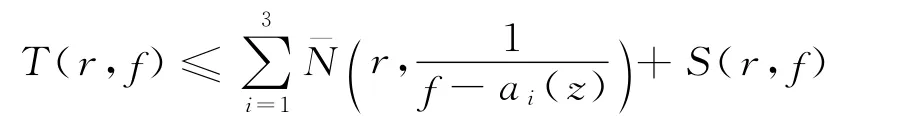
引理6［8］設f是非常數零級亞純函數，q∈＼｛0｝，則在對數測度為1的集合上成立.

引理8［15］設F和G是兩個非常值亞純函數，如果F與G分擔1CM，則下面3個結論必有一個成立：

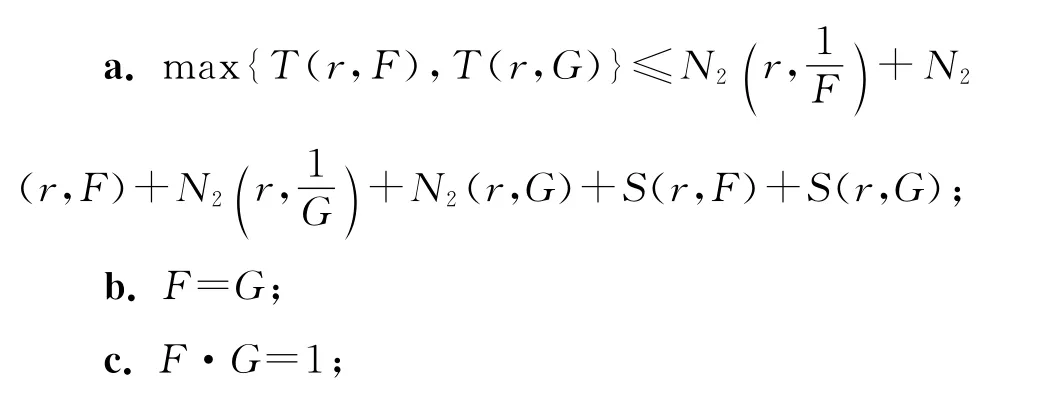
2 定理的證明

由于定理4的證明與定理5的類似，只證明定理4.

2.1 定理4的證明

設F（z）＝fn（z）Δkcf（z），則

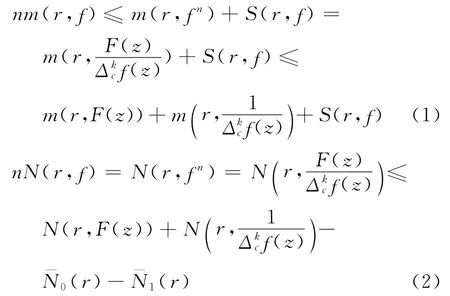
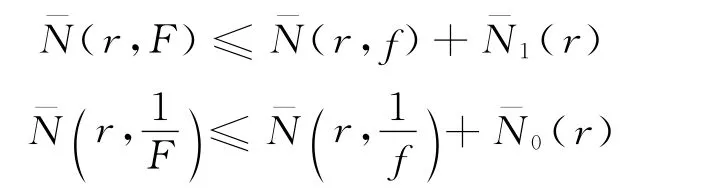
再結合式（1）和式（2）以及引理1、引理5，得

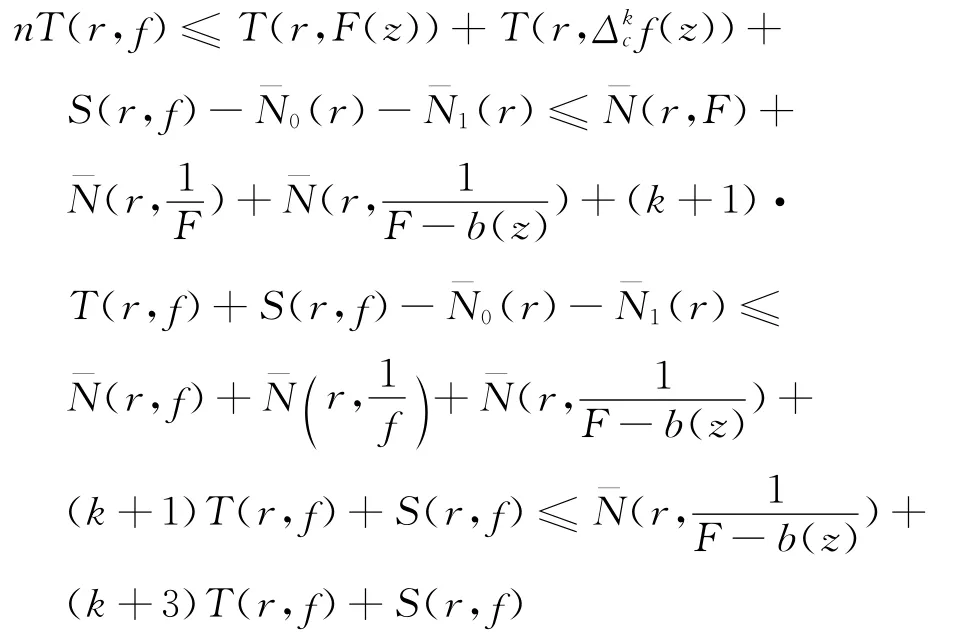
2.2 定理6的證明

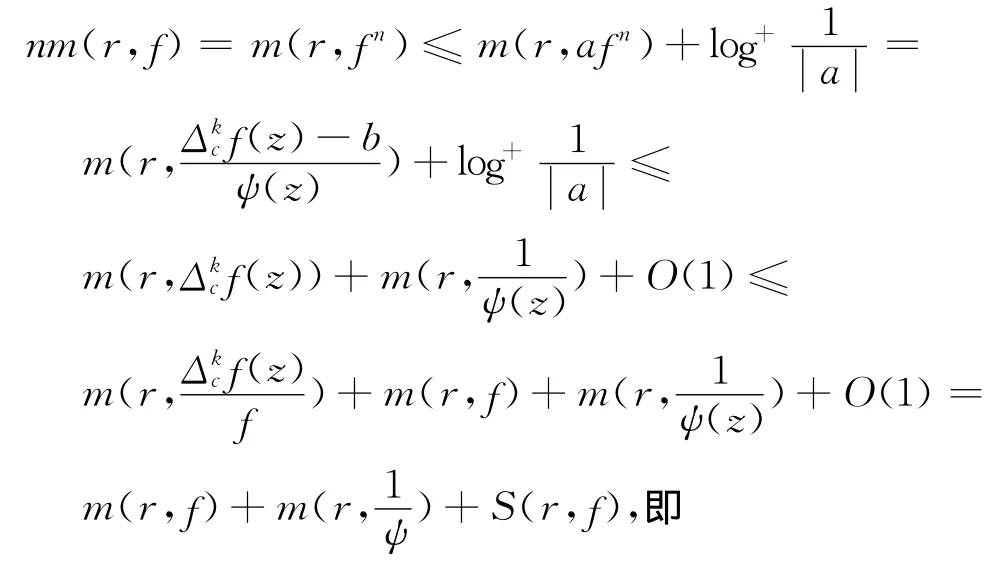
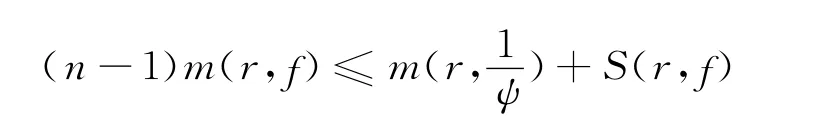
另一方面

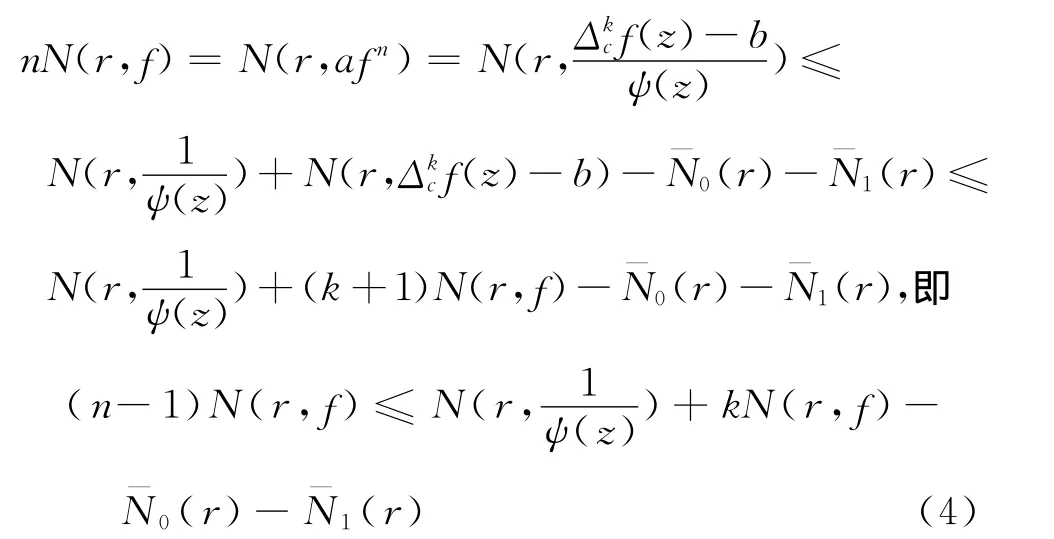
則由式（3）和式（4）及第一、第二基本定理，得

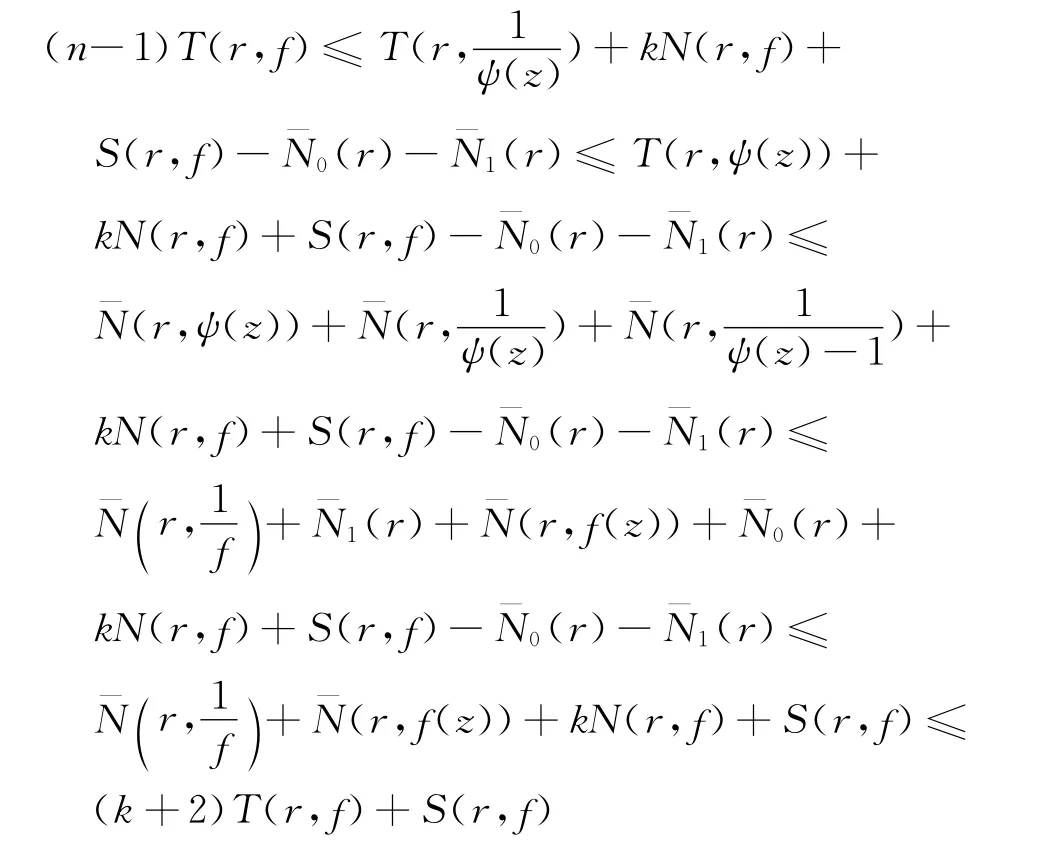
即（n－k－3）T（r，f）≤S（r，f），這與n≥k＋4矛盾.因此，f恒為常數.

2.3 定理7的證明

假設f不是常數，則令

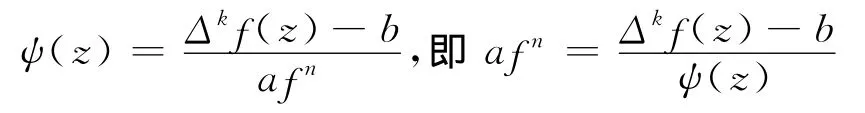
以下考慮兩種情形：

情形1 Δkf（z）≡b.此種情況必有b≠0.

當q≠1時，Δkf（z）＝Δ（Δk－1f（z））＝Δk－1f（qz＋c）－Δk－1f（z），則是Δkf（z）的零點，這與Δkf（z）≡b≠0矛盾；

當q＝1時，f（z）不存在極點，否則若存在，記為z0，那么z0＋c，z0＋2c，…，z0＋kc中至少有一個是f（z）的極點，從而f的級至少是1，這又和條件矛盾，所以f（z）是零級超越整函數，于是Δkf（z）－afn（z）≡b－afn（z）也是零級超越整函數，則Δkf（z）－afn（z）取每個有窮復數無窮多次，這與條件矛盾.

這種情形與定理6的證明類似，此處省略.因此f恒為常數.

2.4 定理8的證明

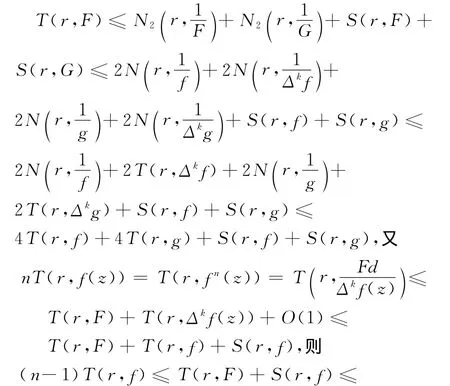
4 T（r，f）＋4 T（r，g）＋S（r，f）＋S（r，g），即（n－5）T（r，f）≤4T（r，g）＋S（r，f）＋S（r，g），同理（n－5）T（r，g）≤4T（r，f）＋S（r，f）＋S（r，g）.

兩式相加，并整理，有

（n－9）（T（r，f）＋T（r，g））≤S（r，f）＋S（r，g）這與n≥10矛盾.因此，由引理8有F＝G或FG＝1.

如果F·G＝1，則fn（z）Δkf（z）gn（z）·Δkg（z）＝d2.由于g是整函數，則零級超越整函數f與Δkf（z）沒有零點，于是f（z）與Δkf（z）是非零常數.而由f是非零常數可知，Δkf（z）恒為零，矛盾.所以F＝G，即fn（z）Δkf（z）＝gn（z）Δkg（z）.

［1］ Hayman W K.Meromorphic functions［M］.Oxford：Clarendon Press，1964.

［2］ 楊樂.值分布理論及其新研究［M］.北京：科學出版社，1995.

［3］ Hayman W K.Picard values of meromorphic functions and their derivatives［J］.Ann Math，1959，70（1）：9－42.

［4］ Mues E.über ein problem von Hayman［J］.Math Z，1979，164（3）：239－259.

［5］ Bergweiler W，Eremenko A.On the singularities of the inverse to a meromorphic function of finite order［J］.Rev Mat Iberoamericana，1995，11（2）：355－373.

［6］ Halburd R G，Korhonen R J.Nevanlinna theory for the difference operator［J］.Ann Acad Sci Fenn，2006，31（2）：463－478.

［7］ Halburd R G，Korhonen R J.Difference analogue of the lemma on the logarithmic derivative with applications to difference equations［J］.J Math Anal Appl，2006，314（2）：477－487.

［8］ Barnett D C，Halburd R G，Korhonen R J，et al.Nevanlinna theory for the q－difference operator and meromorphic solutions of q－difference equations［J］.Proc Math Roy Soc Edinb，Sect A，2007，137（3）：457－474.

［9］ Bergweiler W，Langley J K.Zeros of differences of meromorphic functions［J］.Math Proc Camb Philos Soc，2007，142（1）：133－147.

［10］ Chen Z X，Shon K H.Estimates for the zeros of differences of meromorphic functions［J］.Sci China Ser A，2009，52（11）：2447－2458.

［11］ Chen Z X，Huang Z B，Zheng X M.On properties of difference polynomials［J］.Acta Math Sinica Engl Ser，2011，31（2）：627－633.

［12］ Zhang J L，Gao Z S，Li S.Distribution of zeros and shared values of difference operators［J］.Ann Polo Math，2011，102（3）：213－221.

［13］ Chiang Y M，Feng S J.On the Nevanlinna characteristic of f（z＋η）and difference equations in the complex plane［J］.Ramanujan J，2008，16（1）：105－129.

［14］ Xu J F，Zhang X B.The zeros of q－shift difference polynomial of meromorphic functions［J］.Adva in Diff Equa，2012，2012（1）：200.

［15］ Yang C C，Hua X H.Uniqueness and value sharing of meromorphic functions［J］.Ann Acad Sci Fenn Math，1997，22（2）：395－406.