柔性熱膜剪應力傳感器水下測量溫度修正

馬炳和, 王 毅, 姜澄宇, 李雁冰, 王雷濤

(西北工業大學 空天微納系統教育部重點實驗室, 西安 710072)

0 引 言

流體壁面剪應力的有效測量是實驗流體力學的重要課題，它可為研究分析邊界層狀態提供重要支持，對飛行器及水下航行器的優化設計、減阻增升、主動流動控制，以及自然界的泥沙搬運和沉積、水利工程的抗侵蝕能力等研究具有極其重要的意義。

長期以來，流體壁面剪應力一直沒有有效測量手段。傳統的熱線探針(Hot wire probe)雖然可以通過測量速度梯度來間接計算剪應力，但是由于其近壁測量誤差大、標定使用復雜等缺點，不能滿足流體邊界層內壁面剪應力的測試要求。隨著微機電系統(MEMS)技術的發展，制造敏感尺寸小、分辨率高、壁面貼合性好的熱敏測量元件成為可能[1]。國外的柏林工業大學，加州理工大學等眾多科研機構紛紛開始研究基于MEMS技術的新型剪應力傳感器。其中，美國加州工學院與加州大學洛杉磯分校合作研制出的硅島式熱敏薄膜剪應力傳感器陣列最具代表性，該傳感器已經成功用于邊界層分離的研究[2]。國內的西北工業大學也十分關注先進剪應力傳感器的設計和制造，并成功研制了聚酰亞胺基全柔性熱敏鎳膜剪應力微傳感器陣列[3-5]，開展了相應的風洞/水下測試應用技術研究。該傳感器[6](見圖1)具有動態響應好、空間分辨率高、曲面貼合性好、魯棒性高等特點，能夠廣泛應用于空氣和水下的壁面剪應力測試。

圖1 全柔性熱膜剪應力傳感器陣列[6]

柔性熱膜剪應力傳感器依靠對流傳熱原理來實現邊界層內剪應力測量。因此，其輸出信號與流體溫度有很強的相關性。當測點流體溫度與傳感器的原標定溫度不一致時，傳感器的輸出信號會產生嚴重失真。因此，當傳感器用于非標定溫度流體測量時必須進行溫度修正。

截至目前，溫度影響研究多圍繞流速、流量等測量而展開[7-8]，很少有針對流體壁面剪應力的溫度影響研究。本文專門針對水下壁面剪應力測量，研究水溫對傳感器的影響，提出基于恒溫(CT)驅動的傳感器溫度修正補償方法，并進行實驗驗證。

1 水溫對剪應力的影響

傳感器的測量原理如圖2所示。實際測量中，傳感器貼附于被測表面，并通以適當電流將其加熱。當電流激勵所產生的焦耳熱與流體通過強迫對流換熱作用所吸收的熱量相等時，傳感器與流體達到熱平衡。假設水流溫度均勻一致，此時，傳感器輸出電壓E與被測剪應力τ的關系可用King公式[10]表示：

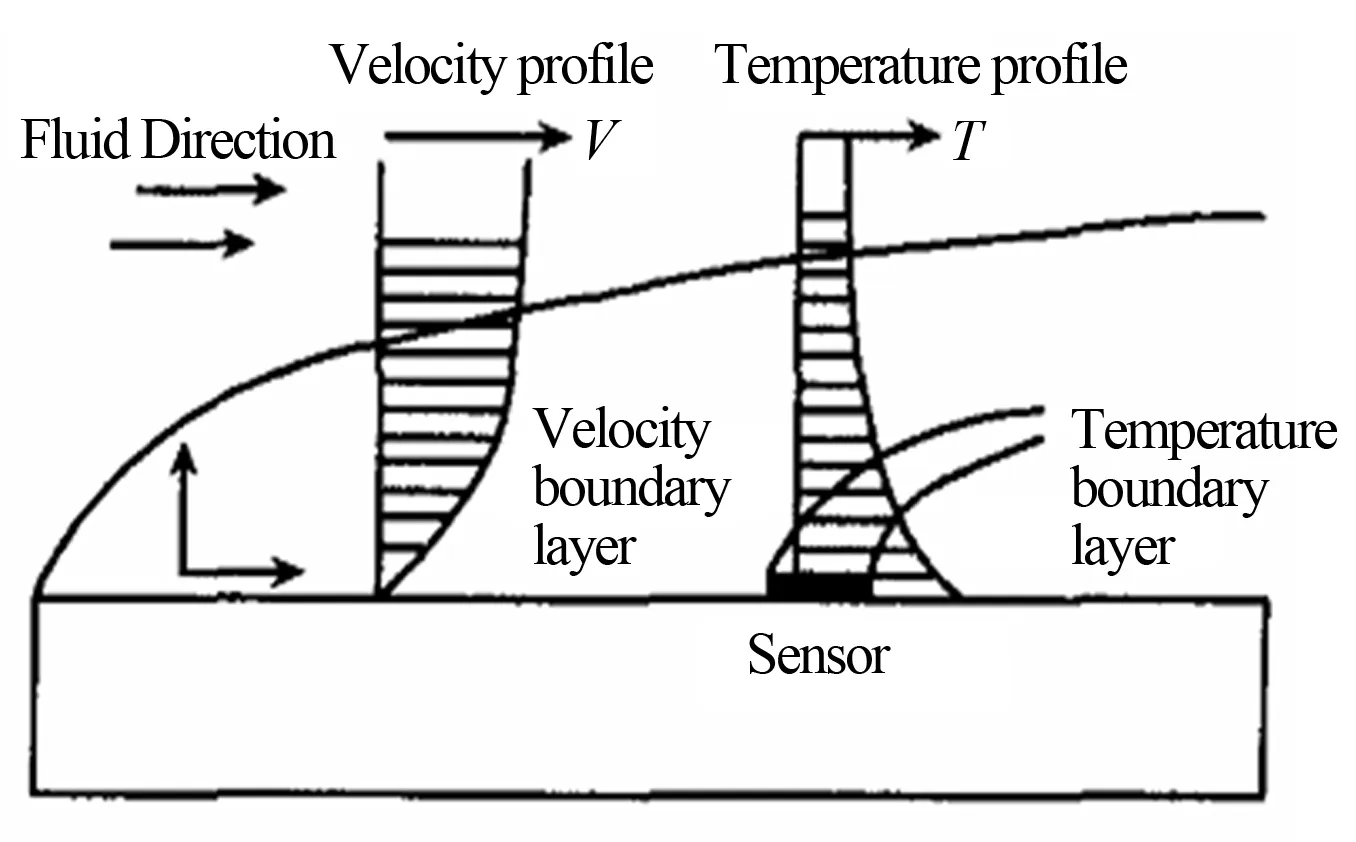
圖2 熱膜剪應力傳感器的測量示意圖[9]

E2/R=(A+B·τ1/3)·(Ts-Tf)

(1)

式中：Tf為水溫，Ts為傳感器敏感元件的工作溫度，且Ts>Tf；R是工作溫度Ts對應的傳感器敏感元件電阻值。

傳感器熱敏膜的電阻溫度系數(TCR)在一定范圍內為定值，溫度差可轉換為敏感阻值差的形式：

(2)

式中：R0是20℃時傳感器的電阻；Rf是流體溫度所對應的敏感元件阻值。阻值R與Rf的比值L為傳感器的過熱比L=R/Rf。在恒溫(CT)驅動模式，敏感電阻值R始終恒定。公式(1)可以用過熱比表示：

(3)

式中：Ac=A·R2/(R0·TCR)；

Bc=B·R2/(R0·TCR)；

Ac、Bc是與流體物性有關的系數。對于水溫Tf下標定的傳感器，當測量環境中的水流溫度與標定不同時，會造成測量誤差。分析公式(3)，溫度影響表現為兩方面：一是水溫Tf變化影響過熱比L；二是流體物性隨溫度變化，引起系數Ac、Bc變化。

1.1水溫對過熱比L的影響

當測試環境水溫相對標定溫度發生偏移時，傳感器的過熱比也隨之變化。對于水下測量而言，設置工作溫度過高會使傳感器敏感元件表面產生氣泡，從而影響測量有效性。因此，傳感器的工作溫度T通常設定為比水溫高20～30℃。對電阻溫度系數TCR為3000ppm/℃的傳感器敏感元件，根據定義L=R/Rf，傳感器的過熱比L取值區間為1.06～1.09(空氣測量中L的設置一般約為1.8)。在如此小的過熱比設置下，溫度偏移所引起的過熱比相對變化比空氣中更為明顯。圖3所示為0～±10℃范圍的水溫偏移對過熱比值的影響，其初始過熱比設置分別為：1.06、1.075和1.09。在0～±10℃范圍，水溫所引起的過熱比誤差范圍分別為±2.75%、±2.79%和±2.83%。

若不考慮水溫對系數Ac、Bc的影響，根據公式(3)，過熱比變化引起的傳感器輸出相對誤差可由公式(4)計算：

(4)

式中：L0為傳感器標定時的初始過熱比。以L0=1.06為例，當水溫偏移±10℃時，傳感器輸出相對誤差為-28.2%～20.8%。水溫偏移對于傳感器輸出的影響如圖4所示。

圖3 水溫偏移對過熱比的影響

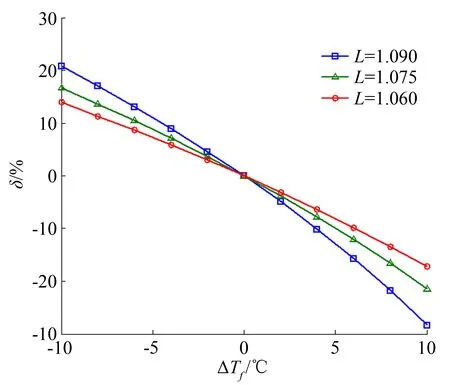
圖4 水溫偏移通過過熱比對傳感器輸出的影響

1.2水溫對系數Ac和Bc的影響

要分析水溫對系數Ac、Bc的影響，必須明確Ac和Bc中與流體相關的物性參量及其與溫度的函數關系。根據H. Kramers對強迫對流換熱系數的研究，公式(1)可表示成努賽爾數Nu的形式[11]：

(5)

式中：As和ls分別為傳感器敏感元件的換熱面積和長度。Re為被測點的雷諾數，Pr為流體的普朗特數，λf為流體的導熱系數。被測點處的剪應力τ與雷諾數Re有如下關系：

τ=0.332·ρυ2·Re3/2

(6)

式中：ρ和υ分別為流體密度和運動粘度。

結合方程(1)、(5)和(6)，可以得到系數Ac和Bc的表達式：

Ac=Ca·λfPr1/5=Ca·fa(T)

(7)

Bc=Cb·λf(Pr/ρυ2)1/3=Cb·fb(T)

(8)

式中：Ca和Cb是與溫度無關的常數。

fa(T)、fb(T)反映了水溫對系數Ac、Bc的影響，與水的密度ρ、動力粘度υ、導熱系數λf、普朗特數Pr等物理性質有關。在0～100℃的溫度范圍內，水的上述物理性質取值參見表1。

表1 水的物理性質與溫度的關系[12]

根據表1，0～100℃內fa(T) 和fb(T)的值與水溫的分布關系如圖5和6所示。

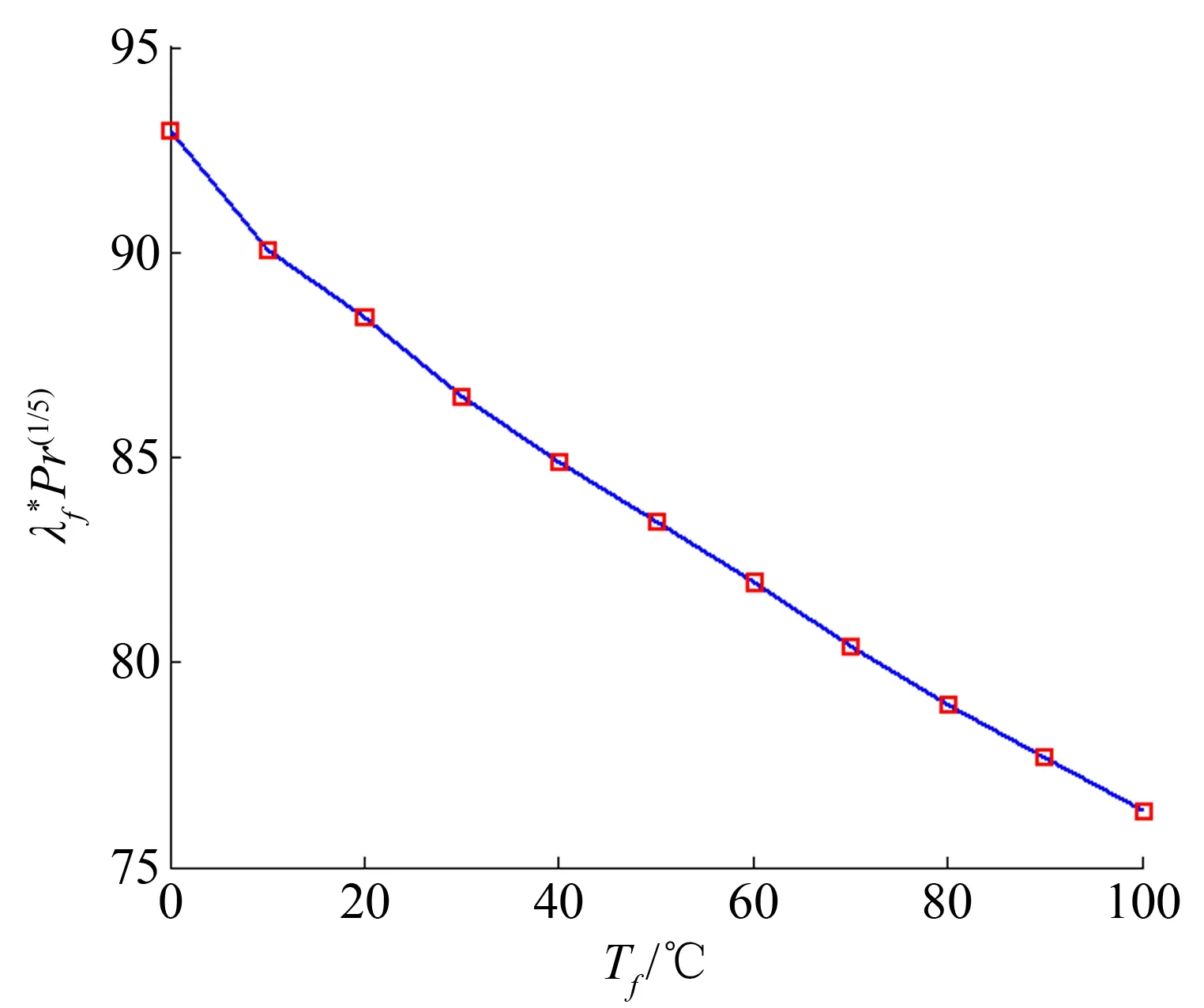
圖5 0～100℃水溫范圍內fa(T) 值

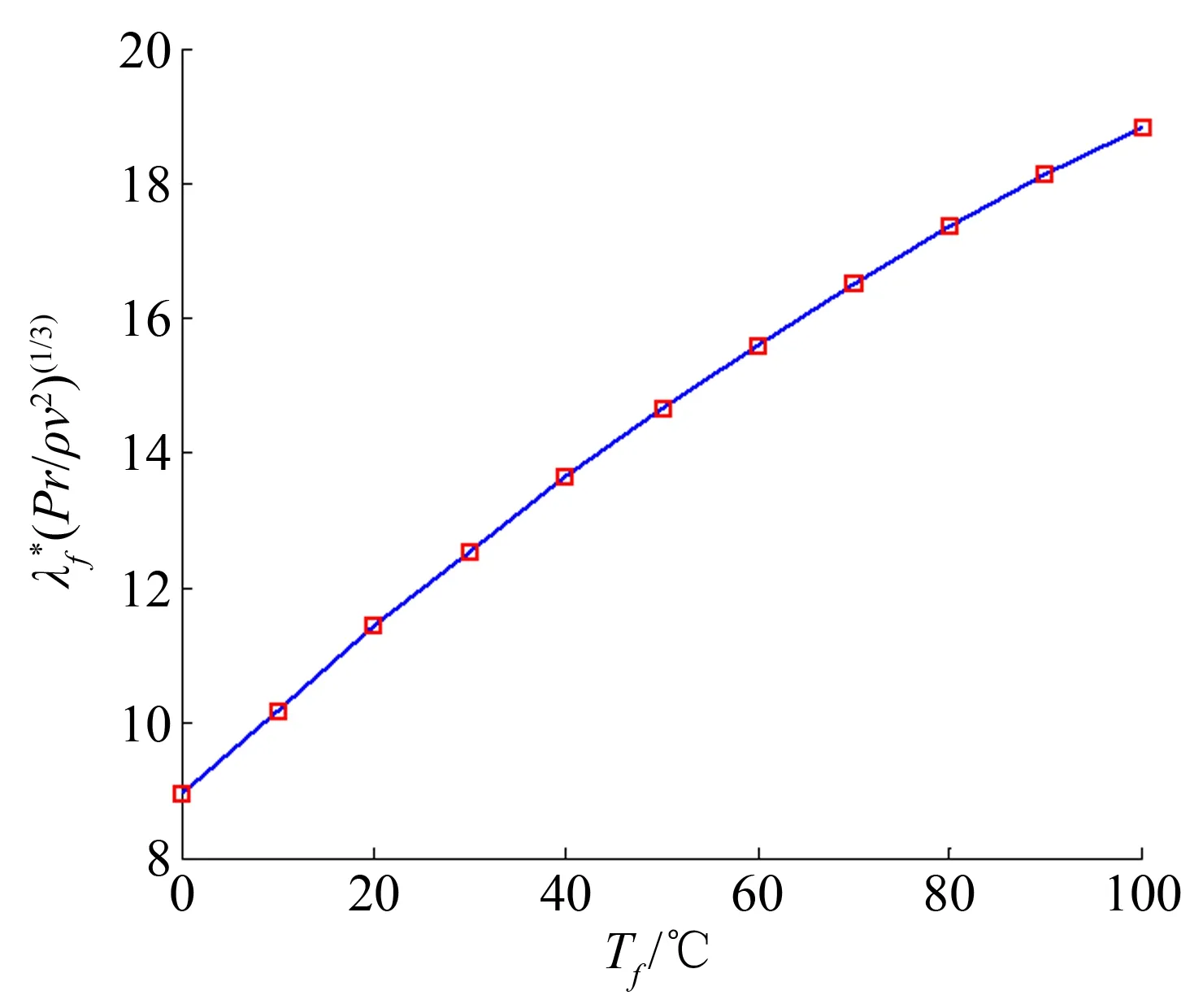
圖6 0～100℃水溫范圍內fb(T) 值

fa(T)、fb(T) 與溫度的函數關系可用多項式回歸獲得，其具體形式如下：

fa(T)=92.52-0.2081×T+4.831×10-4×T2

(9)

fb(T)=8.937+0.1298×T-3.074×10-4×T2

(10)

2 水溫影響的修正方法

目前，國內外基本沒有專門針對流體壁面剪應力的溫度影響研究。空氣中測量時，氣溫對柔性熱膜傳感器輸出的影響只能參照流速測量時的修正方法進行修正[13-14]：

(11)

式中：a、b是常數，a的取值在0.8～0.86之間，b的取值在0.76～0.9之間，Tr為傳感器的標定溫度。

該方法僅能用于空氣測量，并不適用于水下剪應力測量。原因主要有兩個：一是空氣的普朗特數Pr隨溫度波動很小。在0～100℃范圍內，普朗特數為0.688～0.707，可以近似認為其為常數，不受溫度的影響。而相同溫度條件，水中普朗特數變化范圍為1.75～ 13.67，比空氣大很多。普朗特數Pr所受溫度的影響不能忽略。二是水的密度ρ、動力粘度υ和導熱系數λf隨溫度的變化幅度要比空氣中大得多，公式(11)中的指數a和b不再是常數。

因此，針對水下剪應力測量而言，需要考慮建立單獨的溫度修正方法。

假設水溫Tr時，恒溫驅動下的傳感器標定輸出為Er，根據公式(3)有：

(12)

式中：Lr為水溫Tr時的過熱比，Acr、Bcr為水溫Tr下的傳感器標定系數。

在剪應力τ相同的情況下，水溫為T時傳感器的輸出信號E與Er關系如下：

(13)

標定時的輸出Er可表示為：

(14)

實際應用時，假如得到了傳感器在某溫度下的測量輸出E，為獲得被測剪應力，可先依上式推導出標定溫度時對應的傳感器輸出Er，再根據標定公式換算出相應的剪應力值。

由于實際測量中，Acr、Bcr、Lr為已知量。過熱比L可以通過水溫T計算得到。因此，只需計算出系數Ac、Bc的就可求出Er的值。根據公式(7)、(8)可知，Ac、Bc與Acr、Bcr的比值與fa(T)、fb(T)與fa(Tr)、fb(Tr) 比值相等，因此，可以通過引入比值系數α、β來表征Ac、Bc：

(15)

(16)

因此，公式(14)可以變成如下形式：

(17)

可見，公式(17)建立了傳感器測量輸出電壓E與標定輸出參考電壓Er的關系。對于工作在非標定溫度下的傳感器而言，可以借其消除溫度偏移的影響，從而獲得被測剪應力的準確值。

3 實驗與結果分析

上述溫度修正方法的有效性可通過實驗進行驗證。測量不同水溫下傳感器的輸出，并觀察其運用公式(17)進行修正前后相對于參考溫度下傳感器輸出的偏移程度。若修正后傳感器的輸出與參考溫度下的輸出基本重合，則證明該修正方法確實有效。

實驗采用小高寬比的矩形水槽作為剪應力輸入裝置[15]，通過精密的流量計和節流閥的配合，可實現0～10Pa范圍內剪應力的連續輸出。矩形通道橫截面寬度為w=10mm，高度為h=0.6mm，長度為l=100mm。柔性熱膜傳感器平齊放置于水槽底壁上，距注水口45～55mm處，如圖7所示。

圖7 剪應力輸入裝置示意圖

水槽的流量范圍為0～6.2cm3/s，槽內的雷諾數Re<2000，傳感器始終處于層流區域內。水槽底部的壁面剪應力τ與通過矩形橫截面的水流量Q具有對應關系，其計算方法如下：

(18)

式中：n=h/w為水槽橫截面的高寬比；φ(n)為內流通道的形狀修正因子；Dh為內流通道的水力學半徑；μ為水的動力粘度；Q為流經通道的水流量。

實驗中傳感器采用恒溫驅動，其工作溫度設定為40℃，且在整個實驗過程中保持不變；設定測試水流的溫度分別為19.94℃、25.07℃和27.92℃，且在每組測量過程中水溫保持穩定(水溫的變化量ΔT≤0.1℃，測量溫度轉換后的穩定時間大于1h)。實驗結果如圖8所示。

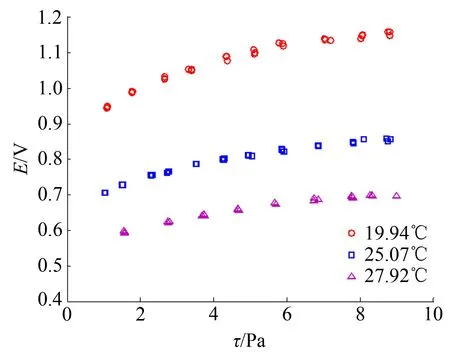
圖8 在不同水溫下傳感器的電壓輸出

將水溫19.94℃作為標定參考溫度，考察相對溫度偏移對于傳感器輸出的影響。從圖8中可以看出，隨著水溫逐次升高，傳感器輸出順次減小，靈敏度也隨之降低。

相對于標定參考輸出，溫度偏移造成的輸出相對誤差如圖9所示。傳感器在25.07℃和27.92℃水溫環境時，其相對誤差大約分別為23.7%、37.1%?？梢?，水溫偏移對傳感器輸出的影響很大，也說明了對傳感器進行溫度修正的必要性。

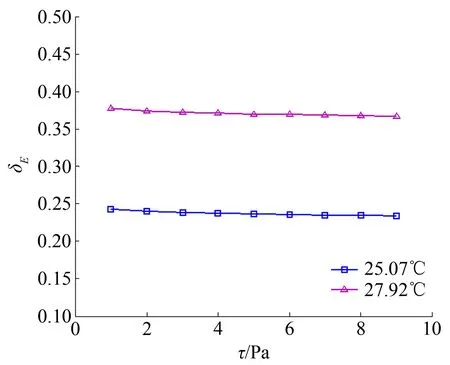
圖9 水溫對傳感器輸出的影響

根據(17)式所建立的傳感器測量輸出電壓E與標定參考輸出Er的關系，分別對水溫25.07℃、27.92℃時的輸出進行修正。其結果如圖10所示。

可以看到，經過補償校正后，傳感器的輸出電壓與標定參考電壓一致。其相對誤差也由23.7%、37.1%減小到了0.82%、0.83%。由此可見，對恒溫系統而言，該修正方法能有效消除水溫偏移對傳感器的影響。

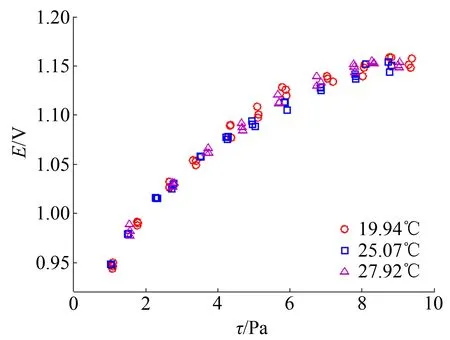
圖10 修正后的傳感器輸出電壓

4 結 論

分析了水下剪應力測量時，溫度對傳感器的影響。從傳感器過熱比、流體物理性質與溫度的關系出發，推導了熱敏剪應力測量行為方程參數與溫度的關系，建立了基于恒溫驅動的水下剪應力測量溫度修正方法。實驗證明，該方法可有效減小不同水溫下傳感器輸出的相對誤差，消除水溫偏移對傳感器的影響，使傳感器輸出更準確反映被測剪應力情況。

致謝:研究得到了國家重大科學儀器設備開發專項項目(2013YQ040911)支持，在此表示感謝。

參考文獻:

[1]Xu Yong. A MEMS multi-sensor chip for gas flow sensing[J]. Sensors and Actuators, 2005, A121: 253-261.

[2]Xu Yong. Flexible shear-stress sensor skin and its application to unmanned aerial vehicles[J]. Sensors and Actuators, 2003, A105: 321-329.

[3]Ma B, Ren J, Deng J, et al. Flexible thermal sensor array on PI film substrate for underwater applications[C]//Micro Electro Mechanical Systems (MEMS), 23rd International Conference on IEEE, 2010: 679-682.

[4]Ren Jinzhong, Ma Binghe. Fully flexible hot film sensor array for underwater applications[C]. Proceedings of the 2010 5th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, 2010: 178-181.

[5]Ren Jinzhong. Fully flexible hot film sensor array for underwater applications[C]. International Conference on Nano/Micro Engineered and Molecular Systems IEEE, 2010, 5th.

[6]馬炳和, 趙建國, 鄧進軍, 等. 全柔性熱膜微傳感器陣列制造工藝及性能優化[J]. 光學精密工程, 2009, 8(17): 1971-1977.

Ma B H, Zhao J G, Deng J J, et al. Fabrication of flexible hot film sensor array and its optimization[J]. Optics and Precision Engineering, 2009, 8(17): 1971-1977.

[7]Bremhorst K. Effect of fluid temperature on hot wire anemometers and an improved method of temperature compensation and linearization without use of small signal sensitivities[J]. Phys E: Sci Instrum, 1985, 18: 44-49.

[8]Bowers C G, Willits D H, Bowen H D. Comparison of temperature correction methods for hot wire anemometers[J]. Transactions of the ASABE, 1988, 31(5): 1552-1555.

[9]馬炳和, 周保清, 鄧進軍, 等. MEMS 微型熱敏傳感器的隔熱結構及其性能分析[J]. 傳感技術學報, 2008, 21(6): 933-937.

Ma B H, Zhao J G, Deng J J, et al. On heat insulation of micro thermal sensor using FEA[J]. Chinese Journal of Sensors and Actuators, 2008, 21(6): 933-937.

[10] King L V. On the convection of heat from small cylinders in a stream of fluid: determination of the convection constants of small platinum wires, with applications to hot-wire anemometry[J]. Proceedings of the Royal Society of London. Series A, 1914, 90(622): 563-570.

[11] Kramers H. Heat transfer from spheres to flowing media[J]. Physica 1946, 12: 61-120.

[12] 楊世銘, 陶文銓. 傳熱學第三版[M]. 北京: 高等教育出版社, 1998: 207-212.

Yang Shiming, Tao Wenquan. Heat transfer 3rd. Edition[M]. Higher Education Press, Beijing, 1998: 207-212.

[13] 張世榮. 熱式氣體流量計溫度補償算法研究[D]. 武漢: 華中科

技大學. 2007.

Zhang S R. Research on thermal gas mass flowmeter and compensation arithmetics[D]. Wuhan: Huazhong University of Science & Technology, 2007.

[14] Sosna C, Buchner R, Lang W. A temperature compensation circuit for thermal flow sensors operated in constant-temperature-difference mode[J]. Instrumentation and Measurement, IEEE Transactions on, 2010, 59(6): 1715-1721.

[15] Xu Yong. Micromachined thermal shear-stress sensor for underwater applications[J]. IEEE Journal of Microelectromechanical Systems, 2005, 14(5): 1023-1030.

作者簡介:

馬炳和(1972-)，西北工業大學教授，博士生導師，微納系統實驗室副主任。研究方向：航空航天微系統、微傳感器及先進測試技術研究。通訊地址：陜西省西安市友誼西路127號(710072)。E-mail：mabh@nwpu.edu.cn