積分第一中值定理的推廣

陳玉

(江西師范大學數學與信息科學學院，江西 南昌330022)

國內外的數學分析及微積分教材中，常見的積分第一中值定理是被積函數乘積因子g(x)在［a，b］上連續且不變號的積分第一中值定理的形式，即:

積分第一中值定理［1］:若f與g都在［a，b］上連續，且g(x)在［a，b］上不變號，則至少存在一點ξ∈［a，b］，使得

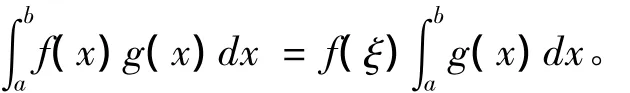
其中，要進一步證明中值點ξ可在開區間(a，b)內取到還另需繁復的證明。

本文將g(x)的條件減弱，用簡便的方法直接得到中值點ξ可在開區間(a，b)內取到的結論，分別得到了閉區間與有限開區間上推廣的積分第一中值定理。

1 閉區間上推廣的積分第一中值定理

引理1［2］:設f(x)在［a，b］上連續，g(x)在［a，b］上有界且有原函數，則f(x)g(x)在［a，b］上有原函數。

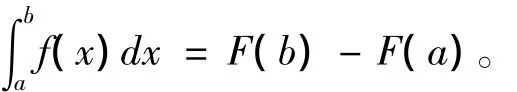
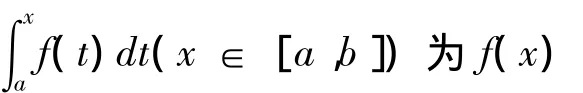
證明:設F(x)為f(x)在［a，b］上的一個原函數，則由引理2可得

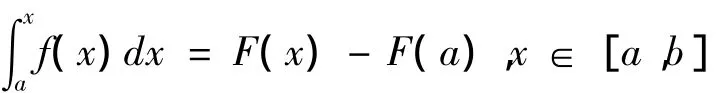
從而

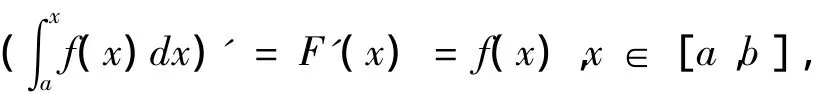
定理1:設f(x)在［a，b］上連續，g(x)在［a，b］上可積且有原函數，g(x)≠0(a＜x＜b)，則存在ξ∈(a，b)，使得

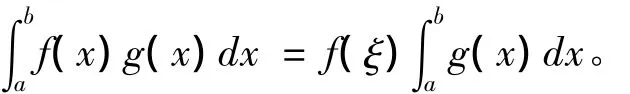
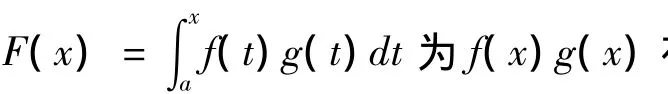
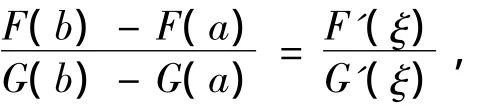
即

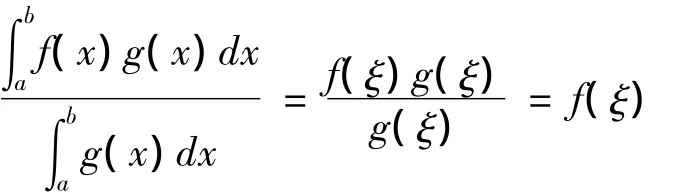
也即

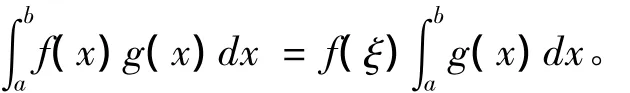
注1:由于可積但不連續的函數也可能有原函數［2］，因此定理1的條件比積分第一中值定理更弱，并且用簡便的證明方法直接得到中值點可在開區間內取到，從而推廣了積分第一中值定理。

注2:定理1也是文獻［4］推論4的推廣。

文獻［4］推論4:設f(x)、g(x)在［a，b］上連續，?x∈［a，b］，g(x)≠0，則存在ξ∈(a，b)，使得

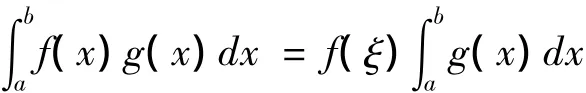
易見，文獻［4］推論4可直接由定理1得到，成為定理1的一個推論，并且還可將條件“?x∈［a，b］，g(x)≠0”放寬為“g(x)≠0(a＜x＜b)”。

注3:定理1也可由文獻［5］定理2(柯西型積分中值定理)直接得到一個更簡潔的證明(見以下證2)。

引理4［5］(柯西型積分中值定理):設f(x)，g(x)在［a，b］上可積，且在［a，b］上有原函數，g(x)≠0(a＜x＜b)，那么存在ξ∈(a，b)，使得

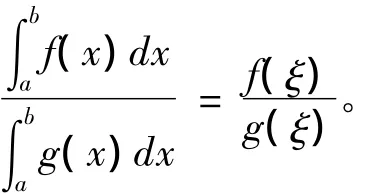
證2:g(x)在［a，b］上可積，從而g(x)在［a，b］上有界。由引理1得，f(x)g(x)在［a，b］上有原函數。又f(x)g(x)在［a，b］可積，f(x)在［a，b］上可……