水平光滑細管內R1234ze冷凝換熱特性實驗研究

李敏霞 楊英英 顧昊翔 馬一太

(天津大學中低溫熱能高效利用教育部重點實驗室 熱能工程系 天津 300072)

低溫室氣體效應制冷工質的使用是目前制冷領域面臨的重要問題，四氟丙烯R1234ze和R1234yf作為替代品已經脫穎而出。參照ASHRAE 34 標準[1]，見表1，R1234ze的ODP值為0，GWP僅為6，遠低于R32和R134a，并且為低毒不可燃物質，與潤滑油有良好的互溶性，與大多數材料具有良好的相容性[2-3]。汪訓昌[4]對比分析了Honeywell公司和日本學者在2009 年公開發表的R1234ze熱物性實驗測試結果，從熱物性方面證明了R1234ze這種不飽和氟化丙烯在替代高GWP 值的HFC 上具有良好的前景。另一方面，科學技術的發展和市場的需求推動了電子設備和機械系統的微小型化，緊湊式換熱器也越來越受到關注，因此新型低GWP制冷劑在小通道內的換熱特性成為了近幾年研究熱點之一。Hossain等[5]用R1234ze在比較常規的通道4.35 mm的水平光管內進行了冷凝實驗，發現其換熱系數比R32低20%～45%，但比R410A高10%～30%。Park等[6]對R1234ze在1.45 mm的豎直小通道內進行了冷凝換熱實驗。發現其換熱系數比R134a低15%～25%。根據Kew和Cornwell[2]提出受限數作為微通道的判據，即認為Co<0.5為常規通道，否則為微通道。管徑4 mm可認定為大通道，而管徑為2 mm時，對R1234ze而言Co值正好接近臨界值0.5。因此觀察此管徑下的換熱情況是有必要的。因此本文選擇研究的管徑為2 mm, 對工質R1234ze水平光滑圓管內的冷凝換熱系數和摩擦壓降特性進行實驗研究和理論分析。

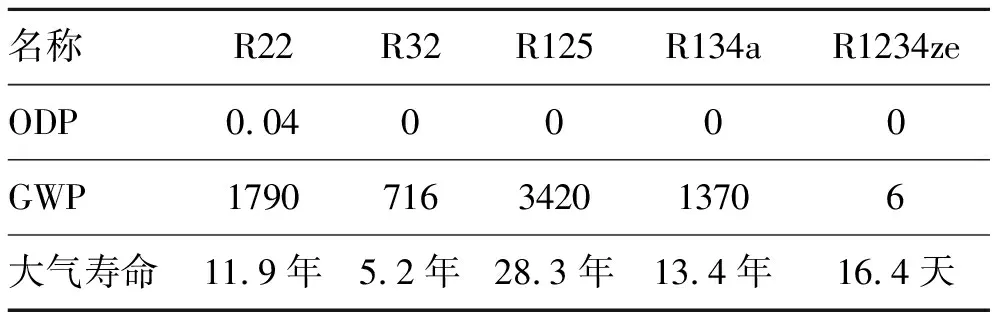
表1 常見制冷劑的ODP、GWP和大氣停留時間

1 實驗系統和數據處理

1.1 實驗系統的介紹

圖1是R1234ze在水平細管內冷凝換熱的實驗系統圖，主要由制冷劑循環、冷卻水循環以及數據測量和采集系統組成。R1234ze流體整個循環過程如下：從冷凝器出來的液態R1234ze流經泵、過濾器、流量計、可視窗后，經預熱段電加熱管被加熱到過熱狀態后進入測試段，在測試段內進行冷凝換熱后流回冷凝器完成一個循環。儲液罐用來調節系統中制冷劑的充灌量。冷卻水循環由恒溫水槽，過濾器，磁力泵，流量計和混水器組成兩段并聯管路。

圖2為測試段整體示意圖，測試段總長為1900 mm，其中總有效換熱長度為1440 mm；分成六小段，每段長為290 mm，有效換熱長度為240 mm，間隔20 mm；中間部分留出30 mm，布置中間壓力測點。

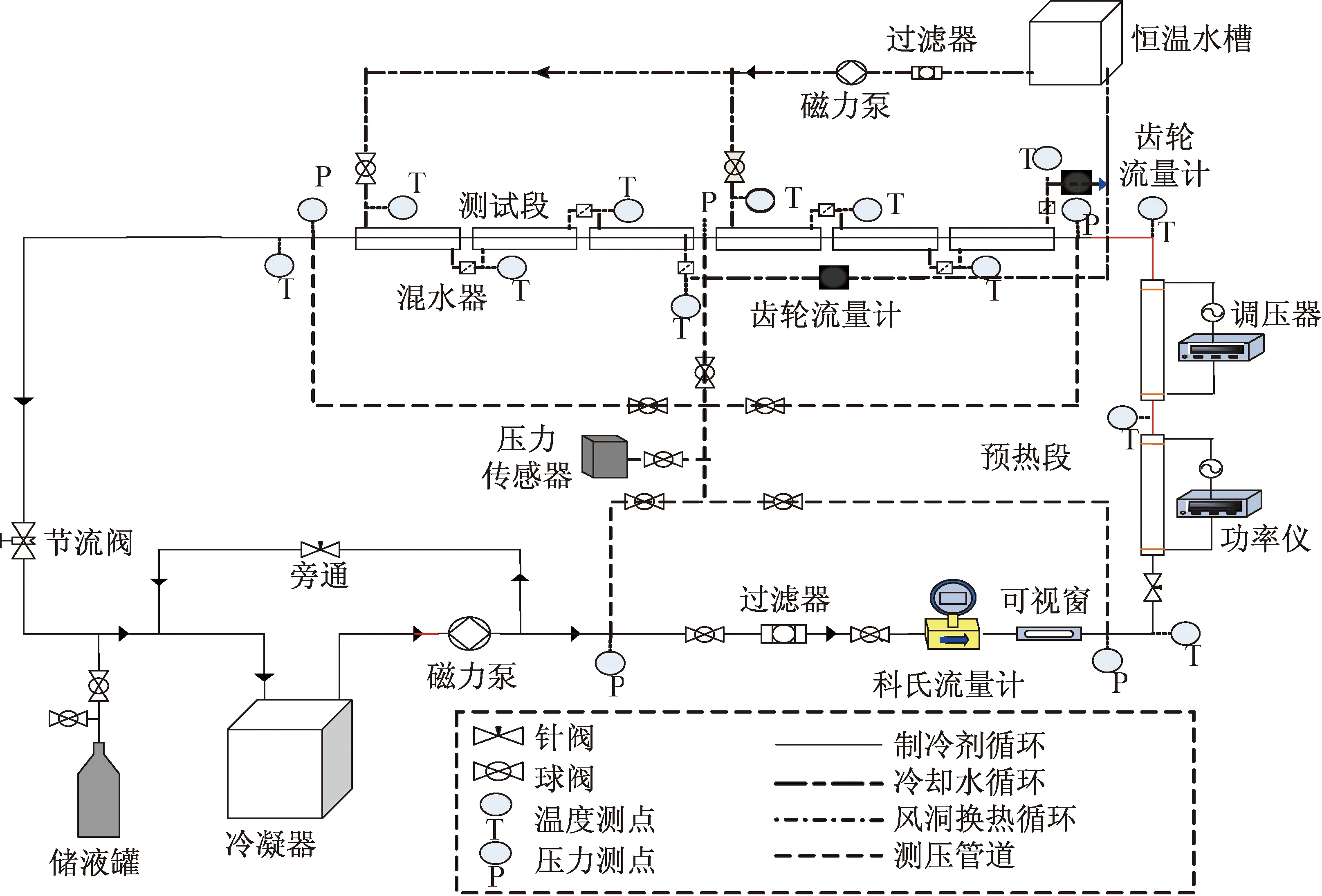
圖1 實驗系統圖

測試段總體為套管結構，制冷劑在管內流動，冷卻水在管外流動，流動方向與制冷劑的流動方向相反，每一段的冷卻水的出口都設置有混水器，混合經過管環的冷卻水，并在每一段的進出口都設置有溫度測點。圖3為測試段截面圖和實物圖。內管為外徑4 mm、內徑2 mm的銅管(純銅)，外管為內徑8 mm、外徑10 mm的銅管(黃銅)。

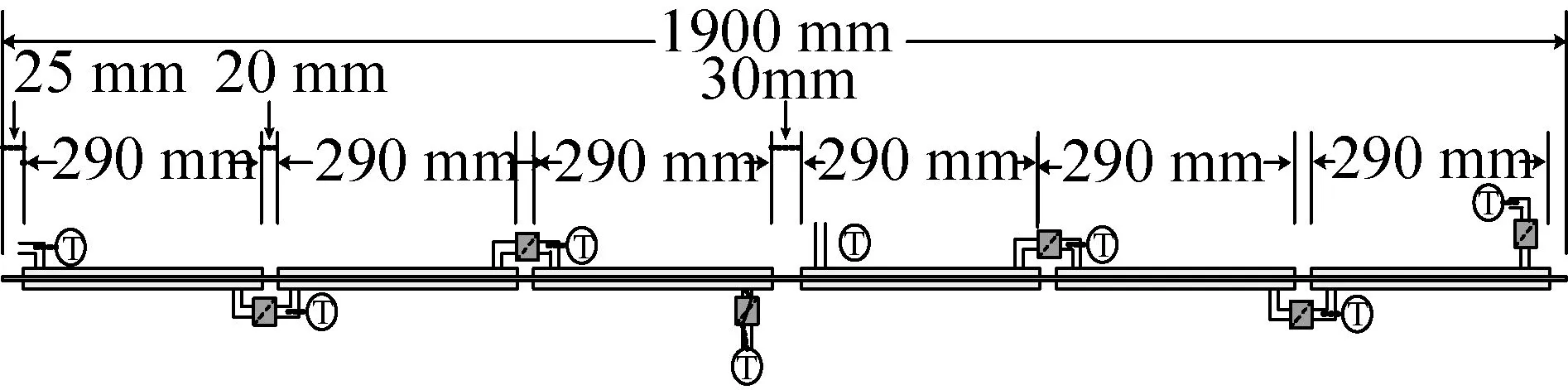
圖2 測試段整體示意圖

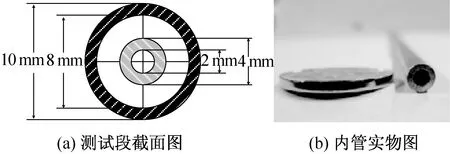
圖3 測試段

1.2 數據處理

為了獲得在一定質量流量和飽和溫度下制冷劑的不同干度的冷凝換熱系數和摩擦壓降，需要進行如下計算。

1)測試段入口干度xin

制冷劑在測試段入口的干度xin即預熱段的出口干度xpre,o,可通過電加熱的能量平衡獲得，制冷劑在預熱段從電加熱獲得的熱量Qpre分為潛熱Qlat和顯熱Qsens兩部分：

Qpre=Qsens+Qlat

(1)

顯熱Qsens為制冷劑從過冷加熱到飽和溫度tsat(測試段入口溫度)所需要的熱量：

Qsens=mrcp,r(tsat-tpre,i)

(2)

潛熱Qlat為制冷劑加熱到一定干度所需要的熱量：

Qlat=mr(hv-hl)xpre,o

(3)

式中：hv和hl分別為制冷劑的飽和氣和飽和液的焓值。

制冷劑的入口干度xin：

(4)

2) 制冷劑的分段換熱量Qr,sub

制冷劑在每一分段的換熱量Qr,sub即分段冷卻水的換熱量Qw,sub：

Qr,sub=Qw,sub=mwcp,w(tw,out-tw,in)

(5)

3) 制冷劑的分段平均干度xm

制冷劑在每一段的平均干度xm為制冷劑在分段的入口干度xsub,i和出口干度xsub,o的算術平均值：

(6)

分段的出口干度可由分段的能量平衡獲得：

(7)

4)分段換熱系數h：

(8)

Ai每一分段的有效換熱面積：

Ai=πdiLsub

(9)

式中：di為內管內徑；Lsub為分段有效換熱長度。

twall,i為測試段內管的內壁溫度：

(10)

式中：do是測試段內管的外徑；λcopper為銅管的導熱系數；twall,o是管外壁平均溫度，為每個分段六個壁溫測點的平均值：

(11)

5)實驗中的總壓降為加速壓降、摩擦壓降和收縮壓降之和。

總壓降：

Δptotal=pin-pout

(12)

摩擦壓降：

Δpfriction=Δptotal-Δpacceleration-Δpcontraction

(13)

其中加速壓降：

(14)

(15)

收縮壓降：

(16)

γ為截面積收縮比：

(17)

式中：A為測試段管內截面積；Al為測試段入口前的管道截面積。

Cc為收縮效率：

Cc=1/(0.639(1-γ)0.5+1)

(18)

1.3 誤差分析

本實驗需要對溫度、壓力、流量和電加熱功率進行測量和采集，數據測量和采集系統包括溫度和壓力傳感器、數據采集系統、功率儀和六位半數字萬用表。各參數的測量存在一定誤差。利用誤差傳遞公式(19)，對換熱系數的可靠性進行了分析。結果見表2，認為測試的換熱系數是可靠的。

N=f(x1,x2,x3)

(19a)

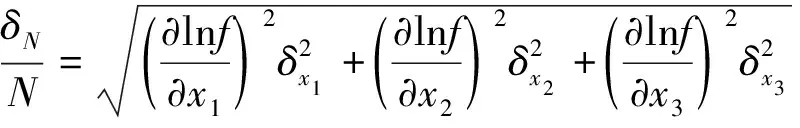
(19b)

在進行冷凝實驗之前進行了熱平衡實驗。經計算實驗系統的漏熱量在6%以內，實驗系統保溫效果較好。

2 結果與分析

2.1 實驗結果

進行冷凝換熱實驗時，設定R1234ze的飽和溫度為35 ℃、40 ℃，質量流量為100～400 kg/(m2·s), 熱流密度4～22 kW/m2。

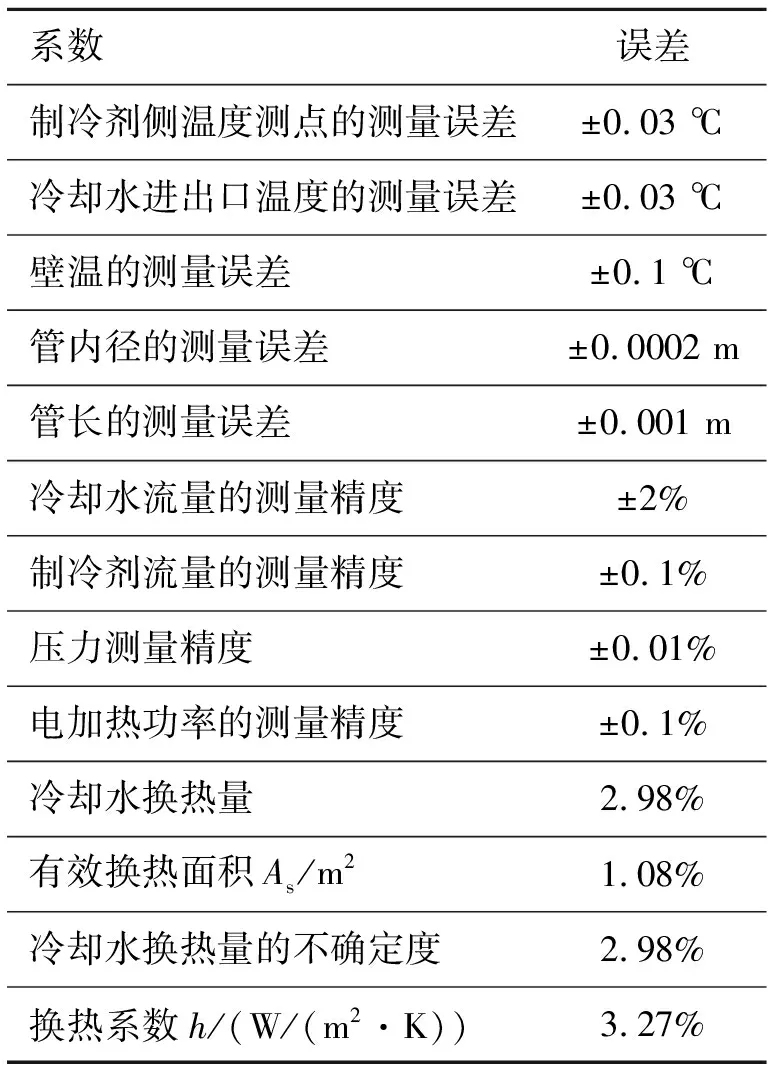
表2 實驗測試的可靠性分析

如圖4所示，在飽和溫度分別為35 ℃和40 ℃時，對不同質量流量情況下的冷凝換熱系數進行了比較。從圖中可以看出，在相同飽和溫度和質量流量下，換熱系數隨干度的升高而增加，且干度大于某一值(稱過度干度值)后，冷凝換熱系數隨干度增加的速率變大；質量流量越大時，該過度干度值越小；相同飽和溫度下質量流量越低時，冷凝換熱系數隨干度增加得越緩慢；在相同飽和溫度下，換熱系數隨質量流量的增加而增大，且在干度較大時，質量流量的影響越明顯。

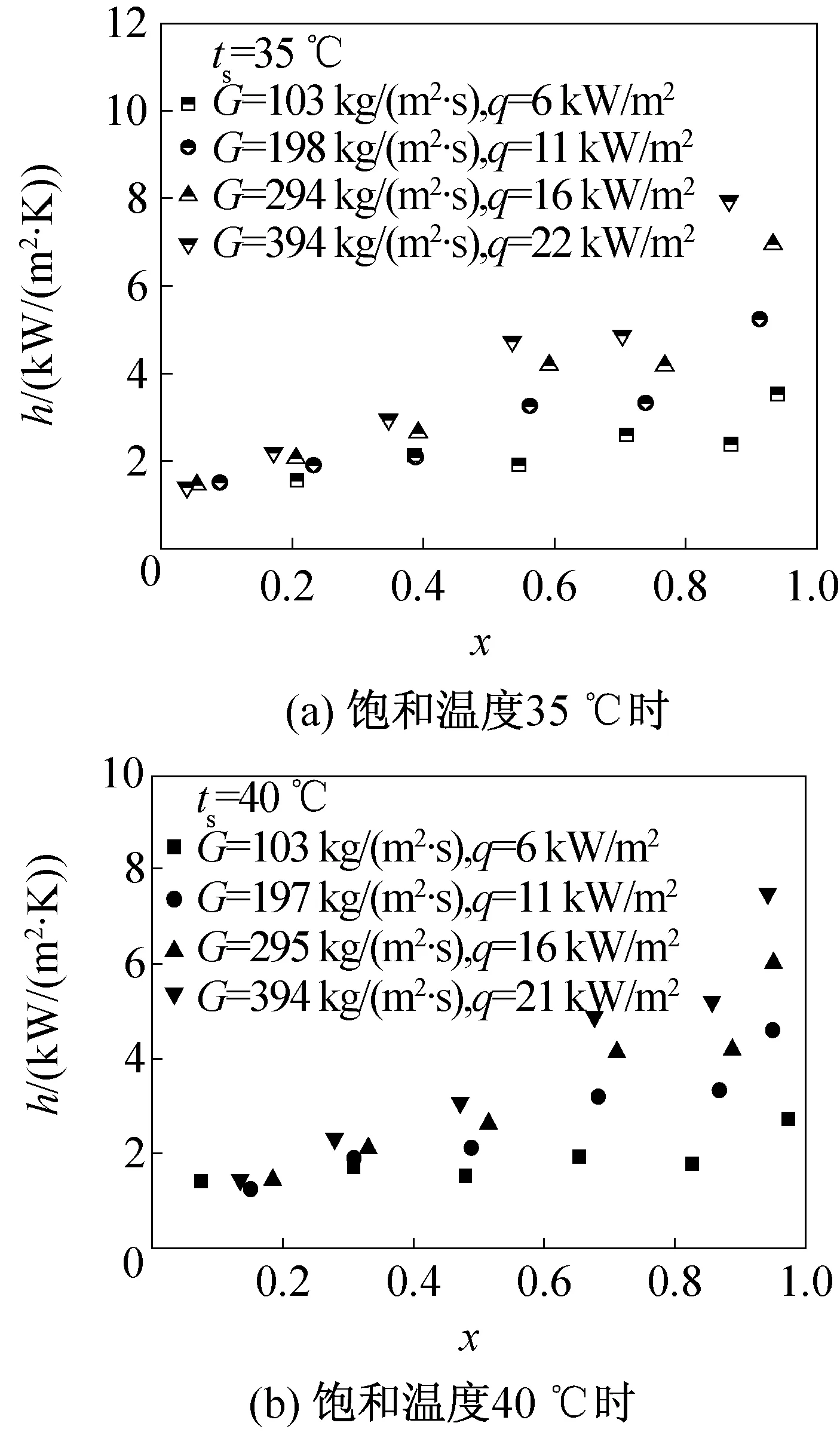
圖4 質量流量對冷凝換熱系數的影響

根據流型分析可知，R1234ze在管內冷凝過程中，干度由大變小，流型從環狀流變化到間歇流，環狀流時，切應力為主要的作用力，質量流量的增加會導致切應力增大，管壁的液膜厚度變小，熱阻減小，因此在干度較大時，質量流量的變化對換熱系數的影響更顯著。質量流量較低時，完全環狀流出現在干度較大的時候，而質量流量較大時，在干度較低的情況下就已經出現環狀流。環狀流時流體換熱受主要受質量流量影響，環狀流時工質的換熱能力比半環流和間歇流更好。

圖5表示了在相同質量流量下冷凝溫度的影響。 可以看出冷凝換熱系數隨飽和溫度的升高而降低，這主要是由于飽和溫度不同導致物性變化造成的。R1234ze的氣化潛熱和液態導熱系數隨著飽和溫度的升高而降低。飽和溫度為35 ℃、40 ℃時，R1234ze的氣化潛熱分別為158.86 kJ/kg和154.64 kJ/kg。

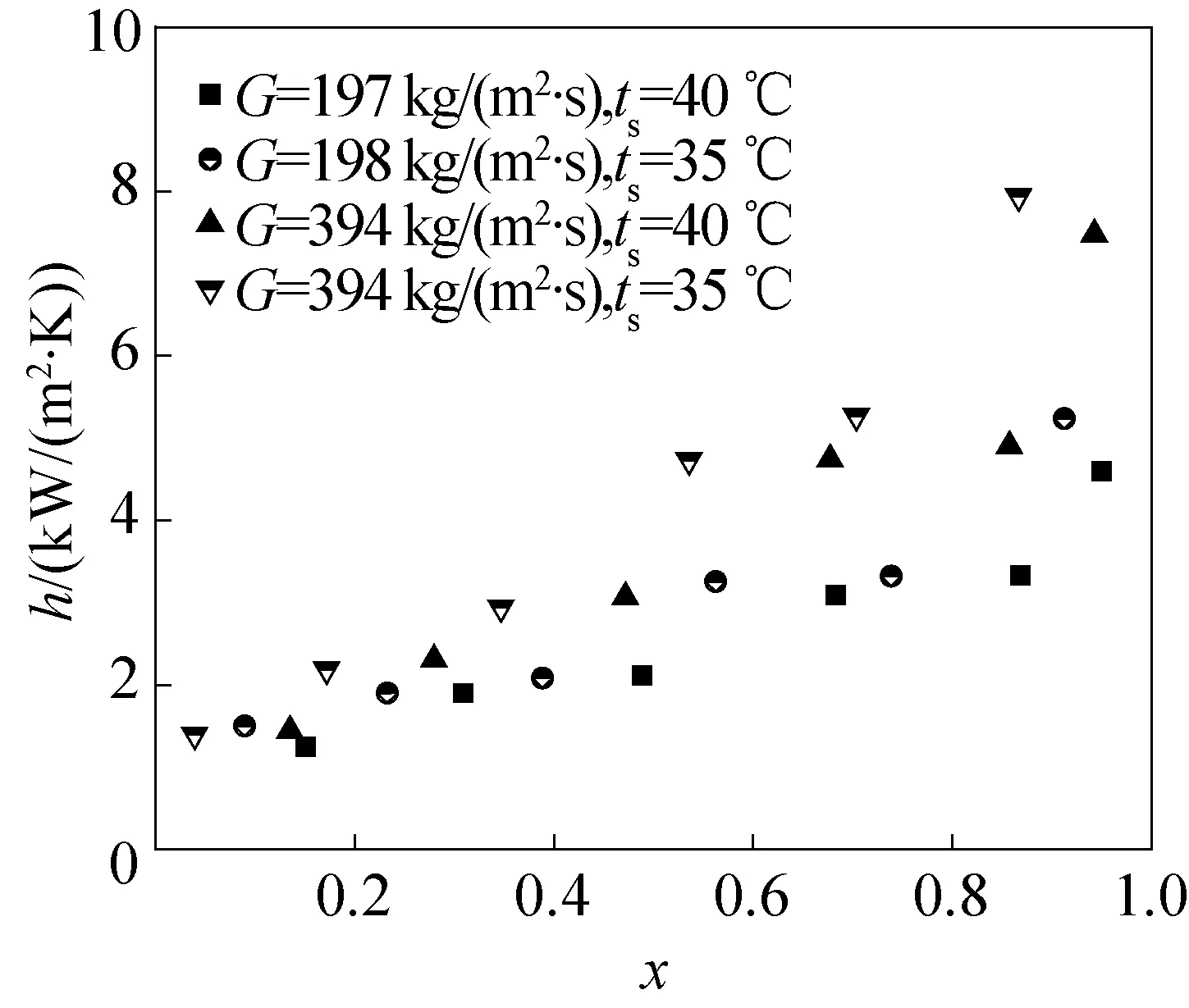
圖5 飽和溫度對換熱系數的影響

圖6比較了飽和溫度40 ℃時，質量流量分別為300、400 kg/(m2·s) 時，不同熱流密度下的換熱系數，通過比較發現，熱流密度的變化對換熱系數幾乎沒有影響。熱流密度改變，即飽和溫度和壁溫的溫差改變，當管內環狀流時，飽和溫度和壁溫溫差對流體換熱系數影響不大。實驗時，流體大部分階段處于環狀流，因此熱流密度對其換熱系數影響不大。Matkovic 等[7]實驗時發現了同樣的現象。

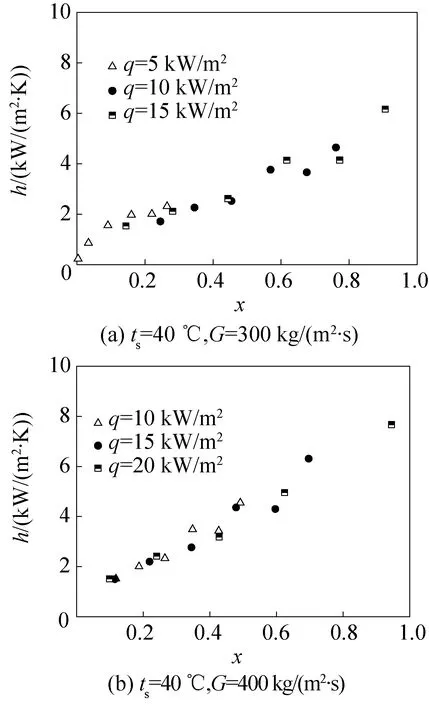
圖6 在不同質量流量下熱流密度對換熱系數的影響

對制冷劑飽和溫度分別為35 ℃和40 ℃時，不同質量流量情況下的摩擦壓降進行了比較，如圖7所示，發現在相同飽和溫度和干度情況下，質量流量越大，摩擦壓降越大；質量流量較低時，摩擦壓降隨干度的變化率較小。

在相同質量流量和干度下，飽和溫度越高，摩擦壓降梯度越小，認為是不同飽和溫度情況下制冷劑物性不同導致的，隨著飽和溫度的升高，R1234ze的粘度降低，因此，由摩擦產生的壓降損失減小；干度越大時，摩擦壓降梯度越大，且隨質量流量的增加，飽和溫度對摩擦壓降的影響越大。

2.2 與其它制冷劑進行比較

將實驗數據與文獻[8]中R32以及文獻[9]中R134a的實驗數據進行對比分析(見圖8)，這些數據都是在2 mm水平光滑管內，飽和溫度40 ℃工況下冷凝換熱的數據。表3列有三種制冷劑在40 ℃時的基本物性參數。從中發現R1234ze的一些物性與R134a非常的接近，R1234ze的液態導熱系數和氣化潛熱比R32和R134a都低。從圖中可以發現R1234ze的冷凝換熱系數比相同工況下R134a的冷凝換熱系數平均低約22 %。R32的冷凝換熱系數最高，其導熱系數和汽化潛熱也最大。R1234ze的冷凝換熱系數比相同工況下R32平均低約31%。

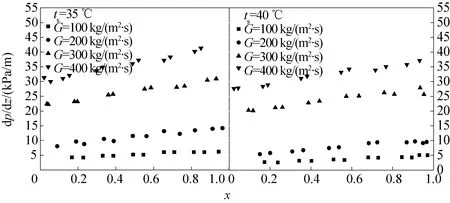
圖7 摩擦壓降實驗值

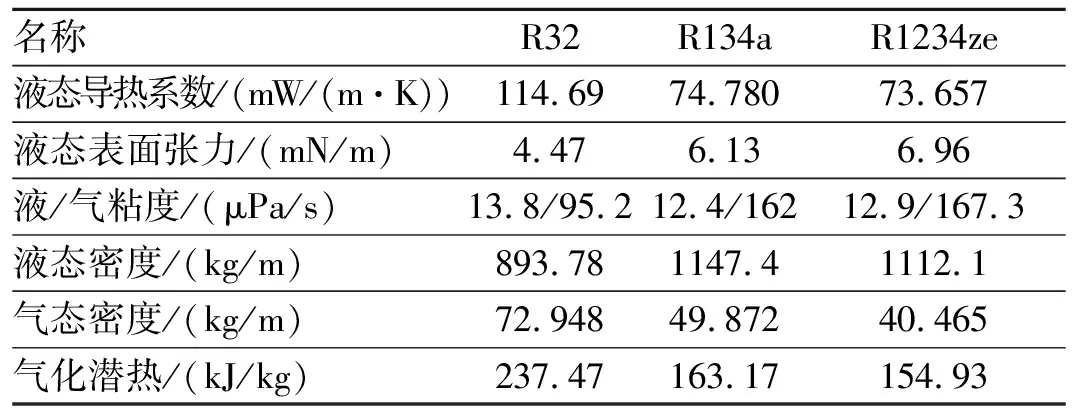
表3 常見制冷劑物性參數

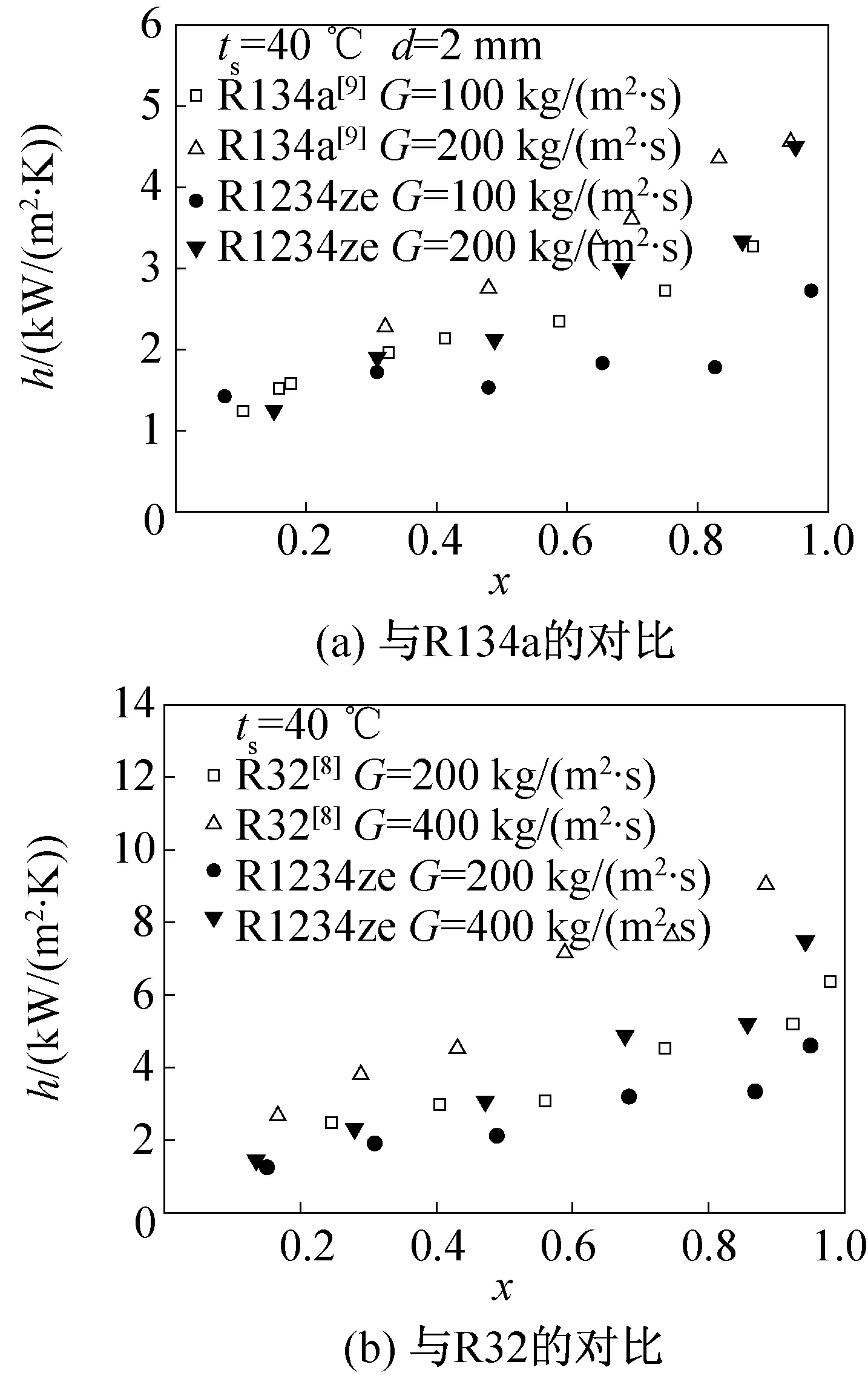
圖8 R1234ze與R32、R134a的傳熱系數實驗值進行對比

圖9為R1234ze的摩擦壓降梯度實驗值與同樣工況下進行冷凝換熱的R32的實驗數據[8]進行比較，從圖中可以看出，R1234ze的摩擦壓降梯度高于R32，這主要是因為R1234ze的氣態粘度明顯高于R32，導致R1234ze的摩擦系數較高。

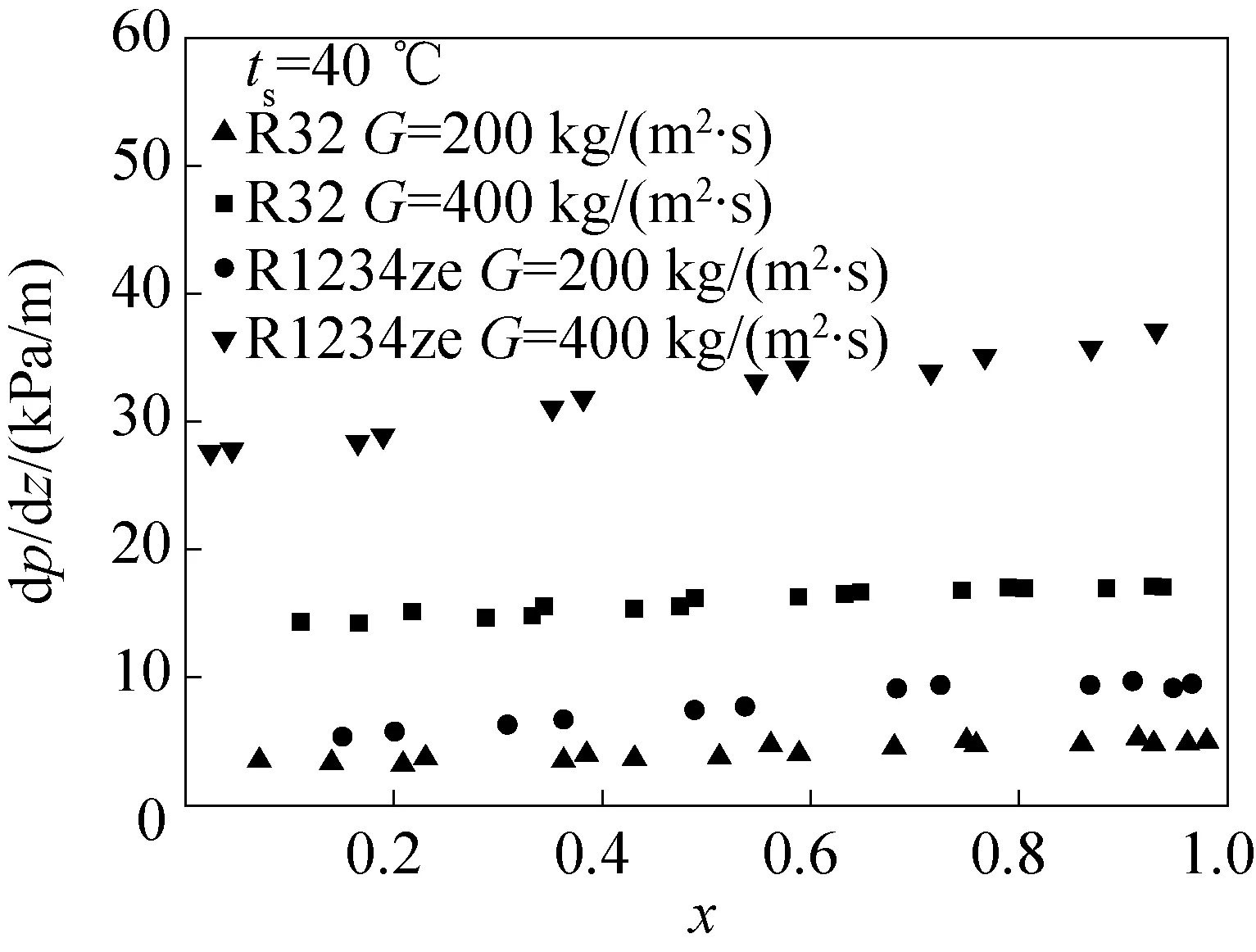
圖9 R1234ze與R32摩擦壓降實驗值對比

2.3 與經典預測模型對比分析

將本實驗結果與六個經典的冷凝換熱模型進行對比分析。分別為Baird等[10]模型、Gerimella[11]模型、Wang[12]模型、Koyama[13]模型、Moser[14]模型、Bandhauer[15]模型。其中Baird等[10]的模型如式 (20)～(25)，其換熱系數與無量綱溫度和壁面切應力有關。

(20)

t+是無量綱溫度，與無量綱液膜厚度δ+有關：

δ+< 5時：t+=δ+Prl

(21)

5≤δ+<30時：

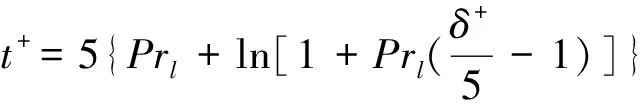
(22)

δ+≥ 30時：

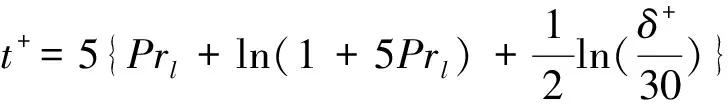
(23)

其中：

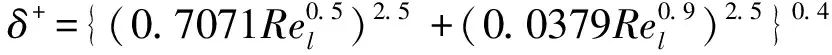
(24)

τw為壁面切應力，與摩擦壓降梯度有關：

(25)

比較結果如圖10，發現圖10(a)中Baird等[10]的模型和圖10 (c)中Gerimella[11]模型對本次實驗的換熱系數預測最好，前者平均絕對誤差為24.03%，其中對65.56%的數據預測誤差在±30%內，后者平均絕對誤差為24.69%，75.56%的數據預測誤差在±30%內。其他Wang[12]模型Koyama[13]模型Moser[14]模型Bandhauer[15]模型四種模型對本次實驗的預測平均絕對誤差都在30%以內，對60%以上的數據預測誤差在±30%內。

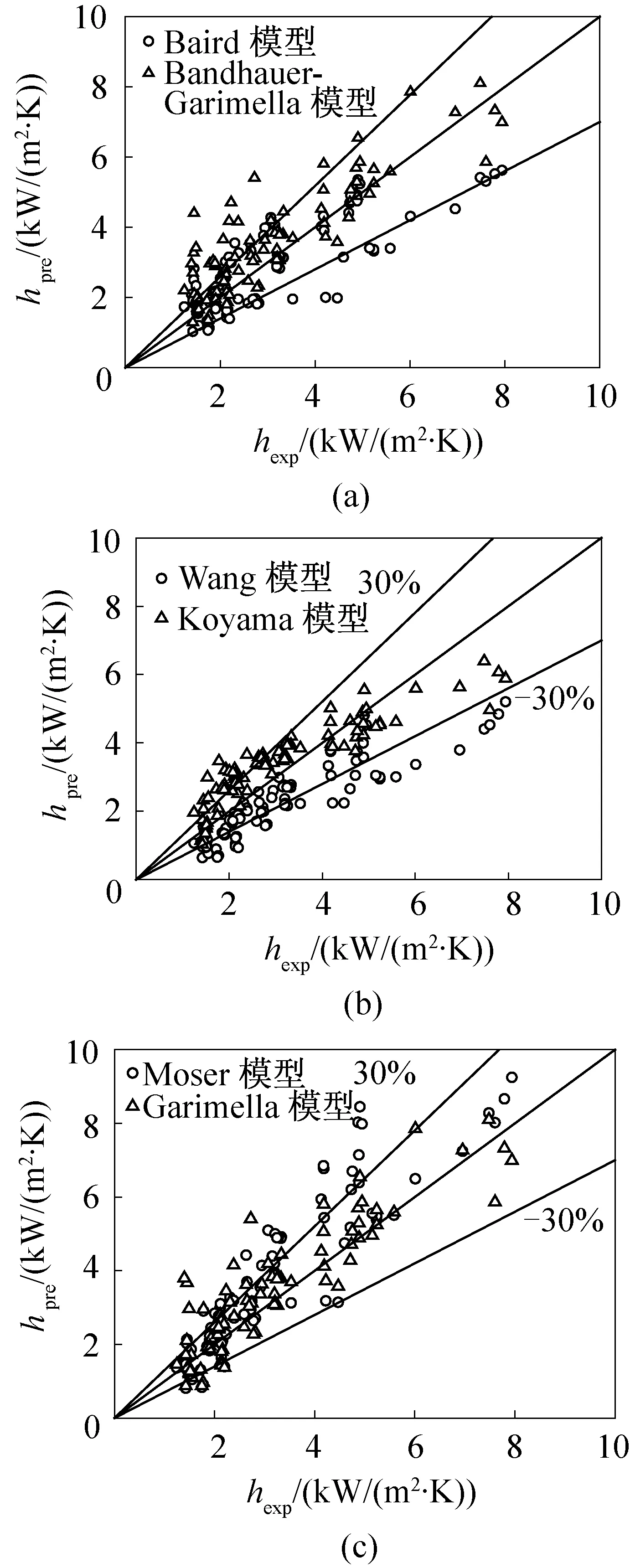
圖10 R1234ze換熱系數實驗值與不同換熱模型比較

同樣，用Baird模型和Gerimella模型對文獻[7-8]中的關于R32的276組實驗數據和文獻[9，16-17]中的關于R134a的193組實驗數據進行預測，預測結果見表4和圖11，可以看出，Baird換熱模型對R1234ze、R134a和R32的預測都較好。

表4 換熱模型對R32、R134a實驗值預測結果

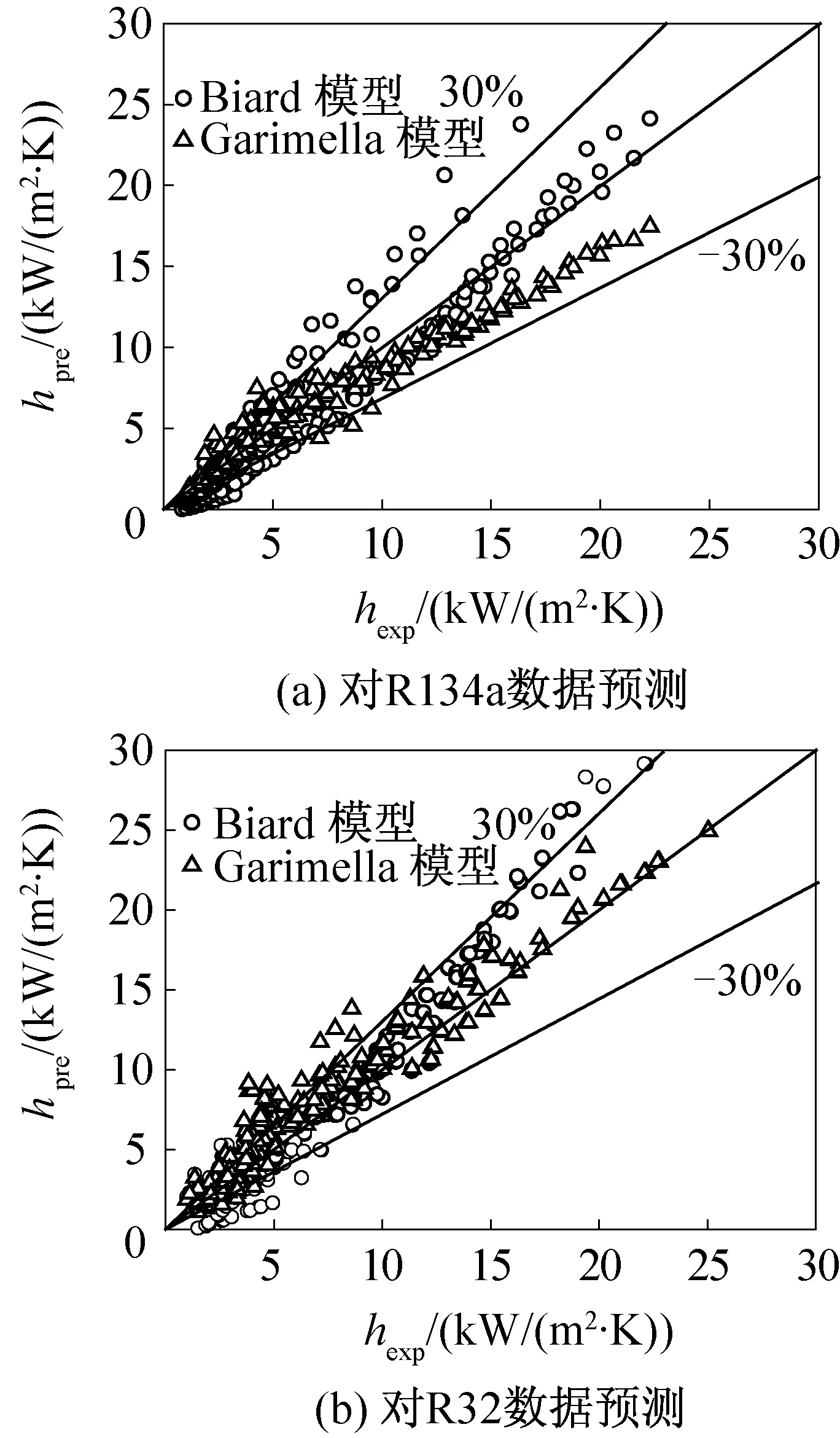
圖11 換熱模型對R32、R134a換熱系數實驗值預測

將本次摩擦壓降的實驗結果與4種摩擦壓降模型的計算結果進行了比較和分析。結果見圖12所示，對于本次實驗的摩擦壓降的實驗結果，Müller-Heck的模型[18]預測最好，平均絕對誤差為25.05%，且對65.63%的實驗數據預測誤差在±30%內。其次，Chisholm的模型[19]平均絕對誤差為29.11%，對56.25%的數據預測誤差在±30%內。而Friedel[20]模型和Zhang-Webb[21]模型對本次實驗結果的預測值偏小。

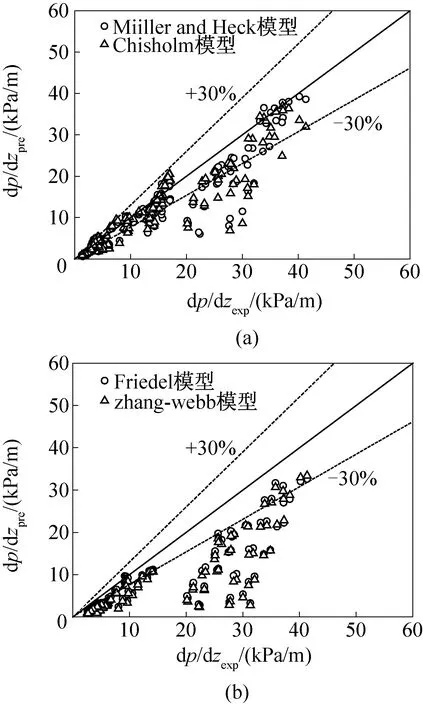
圖12 R1234ze摩擦壓降實驗值和不同預測模型比較

Müller-Heck[18]的模型中摩擦壓降梯度是全液相壓降梯度和全氣相壓降梯度的經驗插值：

(26)

系數F：

F=A+2(B-A)x

(27)

參數A、B分別為全液相和全氣相的摩擦壓降梯度：

(28)

(29)

摩擦系數f計算為：

(30)

其中：

(31)

用Müller-Heck模型和Chisholm 模型分別對文獻[8，17,22]中R32的 222個摩擦壓降實驗數據和文獻[16-17,23]中R134a的185個實驗數據進行預測，預測結果見表5和圖13。

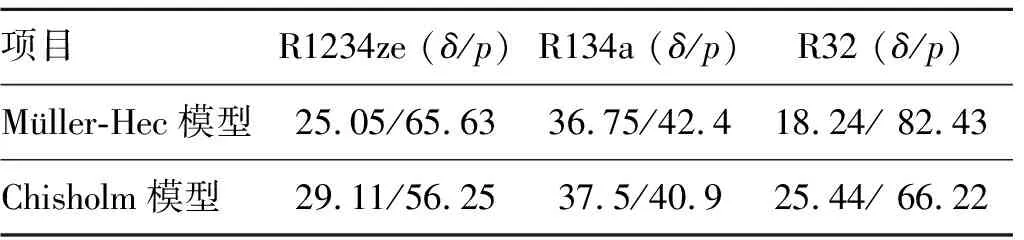
表5 壓降模型對R32、R134a實驗值預測結果

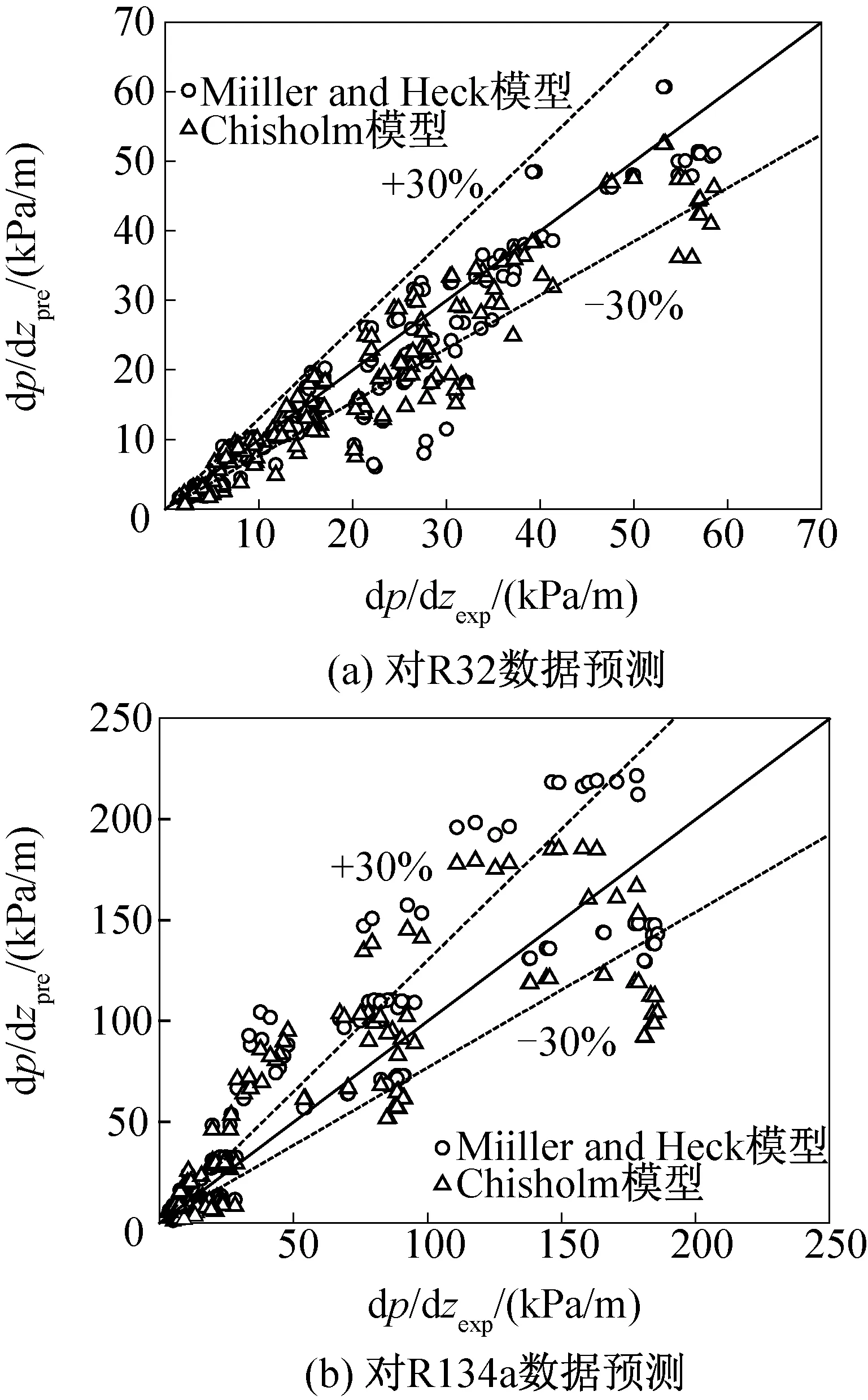
圖13 壓降模型對R32、R134a實驗值預測

3 結論

本文對R1234ze在2 mm 水平光滑管內進行了冷凝換熱實驗研究，同時對實驗數據進行了分析，得出以下結論：

1)當流量在100～400 kg/(m2·s)，冷凝溫度為35 ℃和40 ℃時，R1234ze的冷凝換熱系數范圍在1.5到8 kW/(m2·K)之間時。其冷凝換熱系數隨干度的增加而增加，隨質量流量的增大而增大，隨飽和溫度的升高而降低。

2)在相同工況下R1234ze的冷凝換熱系數比R134a、R32的換熱系數分別平均低大約22%和31%。

3)通過六個換熱模型的對比，發現Baird等[10]的模型和Gerimella模型的預測精度最好。不僅可以很好的預測R1234ze的冷凝換熱系數，對文獻[7-9,16-17]中R32、R134a的實驗數據預測也比較好。

4)實驗中制冷劑的摩擦壓降隨質量流量增加而增加，相同質量流量下，飽和溫度升高，摩擦壓降降低。R1234ze的摩擦壓降梯度高于R32，這主要是因為R1234ze的氣態粘度明顯高于R32，導致R1234ze的摩擦系數較高。Müller-Heck模型和Chisholm模型對R1234ze和R32的摩擦壓降預測較好。

致謝：感謝霍尼維爾(上海)有限公司給與的大力支持和幫助。

[1] Calm J M, Hourahan G C. Physical, Safety, and Enviromental Data for Current and Alternative Refrigerants:Refrigeration for Sustainable Development:proceedings of the 23th International Congress of Refrigeration[C]. Paris： International Institute of Refrigeration, 2011.

[2] Wang Bo，Zhang Wei，Lv Jian. A new refrigerant HFO21234ze [J]. New Chemical Materials，2008，36(2):10-12.

[3] Yang Gang，Yang Hui’e，Li Huili，et al. A new refrigerant—HFO-1234ze and HFO-1234yf[J].Organo-Fluorine Industry，2009(3):16-21.

[4] Wang Xunchang.Summarized thermophysical property measurement results of HFO21234yf and HFO21234ze (E) [J].HV&AC,2010,40(7)：20-39.

[5] Md Anowar Hossain, Yoji Onaka, Akio Miyara. Experimental study on condensation heat transfer and pressure drop in horizontal smooth tube for R1234ze(E), R32 and R410A[J]. International Journal of Refrigeration,2012,35: 927-938.

[6] J E Park, F Vakili-Farahani, L Consolini, et al. Experimental study on condensation heat transfer in vertical minichannels for new refrigerant R1234ze(E) versus R134a and R236fa [J]. Experimental Thermal and Fluid Science, 2011,35: 442-454.

[7] M Matkovic, A Cavallini, D Del Col, et al.Experimental study on condensation heat transfer inside a single circular minichannel[J].International Journal of Heat and Mass Transfer, 2009, 52: 2311-2323.

[8] Yang Yingying, Li Minxia, Ma Yitai. Heat transfer Characteristics for Condensation of R32 in a Horizontal Small Tube [C]//2013 Heat and Mass Transfer Conference of CSET. Chongqing, China.

[9] Yi-Yie Yan, Tsing-Fa Lin.Condensation heat transfer and pressure drop of refrigerant R134a in a small pipe[J].International Journal of Heat and Mass Transfer, 1999, 42: 697-708.

[10] J R Baird, D F Fletcher, B S Haynes.Local condensation heat transfer rates in fine passages[J].International Journal of Heat and Mass Transfer, 2003, 46: 4453-4466.

[11] Srinivas Garimella, Akhil Agarwal, Todd M Bandhauer. Channel Size Based Messurement Techniques for Condensation Heat Transfer Coefficients in Mini-and Micro-Channels[C]//2005 ASME International Mechanical Engineering Congress and Exposition, November 5-11, 2005, Orlando, Florida, USA.

[12] Wei-Wen William Wang, Thomas D Radcliff, Richard N Christensen. A condensation heat transfer correlation for millimeter-scale tubing with flow regime transition[J]. Experimental Thermal and Fluid Science ,2002, 26:473-485.

[13] S Koyama, K Kuwara, K Nakashita. Condensation of refrigerant in a multi-port channel [C]//First International Conference on Microchannels and Minichannels,Rochester,NY, 2003:193-205.

[14] Moser K W, Webb R L, Na B.A New Equivalent Reynolds Number Model for Condensation in Smooth Tubes[J].Heat Transfer,1998,120(2):410-417.

[15] Todd M Bandhauer, Akhil Agarwal, Srinivas Garimella. Measurement and Modeling of Condensation Heat Transfer Coefficients in Circular Microchannels[J].Transactions of the ASME,2006,128:1050-1059.

[16] M H Kim, J S Shin, C Huh, et al.A study of condensation heat transfer in a single mini-tube and a review of Korean micro-and mini-channel studies[C]//First International Conference on Microchannels and Minichannels, Rochester, NY, 2003, Apr: 47-58.

[17] Alberto Cavallini, Davide Del Col, Marko Matkovic, et al. Pressure Drop During Two-Phase Flow of R134a and R32 in a Single Minichannel[J].Journal of Heat Transfer, 2009,131(3): 033107-033115.

[18] H Müller-Steinhagen, K Heck.A simple friction pressure drop correlation for two-phase flow in pipes[J].Chem. Eng. Process., 1986 (20) 297-308.

[19] D Chisholm. Two-Phase Flow in Pipelines and Heat Exchanger[M]. Longman Book Inc., New York, 1983.

[20] L Friedel. Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow[M].European Two-phase Group Meeting, Ispra, Italy, 1979, E2.

[21] Ming Zhang, Ralph L Webb. Correlation of two-phase frictionfor refrigerants in small-diameter tubes[J]. Experimental Thermal and Fluid Science, 2001 (25): 131-139.

[22] Alberto Cavallini, Stefano Bortolin, Davide Decl Col, et al. Condensation Heat Transfer and Pressure Losses of High-and Low-Pressure Refrigerants Flowing in a Single Circular Minichannel[J]. Heat Transfer Engineering, 2011,32(2): 90-98.

[23] Yi-Yie Yan, Tsing-Fa Lin. Condensation heat transfer and pressure drop of refrigerant R134a in a small pipe[J]. International Journal of Heat and Mass Transfer, 1999, 42: 697-708.