基于遺傳算法的分布式電源選址與定容

薛 濤 湯亞芳

（貴州大學電氣工程學院，貴州 貴陽 550025）

0 引言

分布式發電(Distributed Generation，簡稱DG)是指將發電系統以小規模(發電功率在數千瓦至50MW的小型模塊)、分散式的方式布置在用戶附近,可獨立地輸出電能的系統[1]。分布式電源接入配電網，對配電網的節點電壓、線路潮流、短路電流、網絡可靠性等都會帶來影響,其影響程度與分布式電源的位置和容量密切相關。因此，合理的選擇分布式電源的位置和容量非常重要[2]。

基于分布式電源對配電網規劃的重要影響，本文在分布式電源的位置和容量均不確定的情況下，考慮以配電網網損最小和DG的運行費用最小為目標函數，建立了含分布式電源選址與定容的多目標規劃模型[3]，并用遺傳算法對分布式電源的位置和容量進行優化，得到分布式電源的優化配置方案。

1 含DG的配電網規劃模型

1.1 目標函數

綜合考慮分布式電源接入配電網后的網絡損耗費用和運行費用，建立歸一化數學模型如式（1）所示：

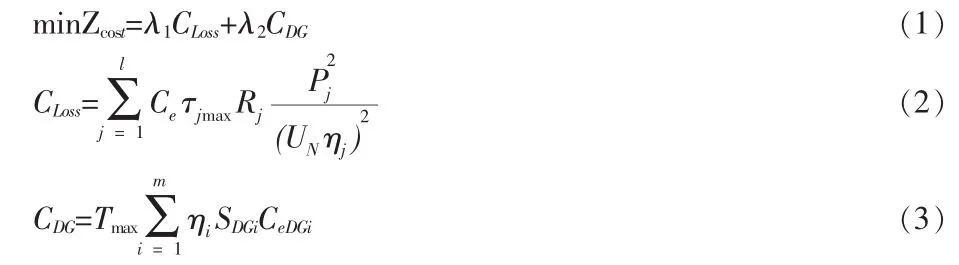
式中：Zcost為總費用，即歸一化目標函數；CLoss、CDG分別表示分布式電源接入配電網后的年網絡損耗費用、年運行費用，如式（2）、（3）所示，Ce（元/kWh）為單位電價，τjmax為支路j的年最大負荷損耗小時數，Rj為支路j的電阻，Pj為流過支路j的有功功率（kW），UN為線路的額定電壓，ηj為線路流過的負荷功率因數，Tmax為分布式電源的最大發電小時數，m為接入配電網的分布式電源的總個數，ηi為分布式電源i的功率因數，SDGi為第i個分布式電源的容量（kVA)，CeDGi為第i個分布式電源的單位電量成本 （元/kWh）；λ1、λ2為對應費用的權重系數，0<λ1，λ2<1且 λ1+λ2=1。

1.2 約束條件

（1）節點電壓約束條件

Uimin≤Ui≤Uimax

式中，Ui為節點 i的電壓；Uimin、Uimax分別為 Ui的上下限。

（2）支路電流不等式約束

Ij≤Ijmax

式中，Ij、Ijmax分別表示第j條支路的電流和允許通過的電流上限。

（3）潮流約束

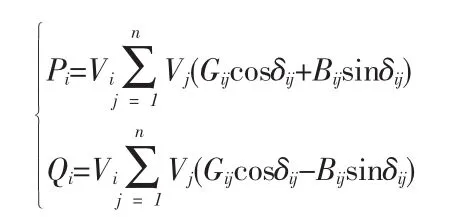
式中，Pi、Qi分別為節點 i注入的有功和無功功率；Gij、Bij、δij分別為節點 i、j間的電導、電納和電壓相角差；n為系統節點總數；Vi、Vj分別為節點i、j的電壓幅值。

2 含DG的配電網潮流計算

接入配電網中的分布式電源所采用的模型，既可以簡化成PV節點、也可以是PQ節點，本文將其簡化成具有恒定功率因數的PQ節點[4]。由于分布式電源一般靠近負荷中心，所以假設分布式電源的位置在負荷節點上。本文對接入分布式電源的配電網采用前推回代法進行潮流計算[5]，這種潮流計算方法首先假定各節點電壓均等于根節點電壓，從末端節點開始，由己知的各節點負荷功率、節點電壓，向輻射狀配電網始端推算各支路的電流以及始端功率。然后由始端向末端推算各節點電壓，如此重復以上過程直至迭代收斂為止。

3 分布式電源選址與定容的求解

由于遺傳算法具有較好的全局搜索性能、搜索過程不容易陷入局部最優等優點，考慮分布式電源選址定容的特點，本文采用遺傳算法求解分布式電源的位置與容量。

3.1 遺傳算法

遺傳算法[6]是一種模仿生物界自然選擇和自然遺傳機制的隨機搜索算法，它通過某種編碼技術，作用于稱為染色體的數字串，對由這些串組成的群體的進化過程進行模擬，并通過有組織的、隨機的信息交換來重組那些適應性好的串，生成新一代群體。遺傳算法以其簡單、通用性強、不依賴問題模型等特性，已在函數優化等領域獲得廣泛應用。

（1）染色體編碼

本文對DG的選址定容染色體編碼采用實數編碼，因此一個允許n個節點安裝分布式電源的配電網絡，分布式電源的選址定容方案可以用一組變量C={C1，C2，……，Cn}表示，Ci的數值大小表示節點i的分布式電源建設情況，若Ci=0則表示該節點沒有安裝分布式電源。

（2）遺傳操作

遺傳算法包括三個基本操作：選擇、交叉、變異。通過以適應度函數為依據，對群體進行這三個操作步驟，實現個體之間的信息交換與重組，使群體的適應度不斷提高，最終得到全局最優解。本文采用的三種遺傳算子如下。

選擇算子：選擇運算使用比例選擇算子來淘汰種群中的劣質個體，保留其中優良個體。選擇算子中的選擇原理采用比例選擇原則，如果假設種群數為M，個體i的適應度為fi，則個體i被選擇的概率為：

交叉算子：為了降低優良個體被破壞的可能性，本文在交叉過程中采用動態交叉概率，即設定迭代初期交叉概率值Pc0=0.95，在迭代后期取較小的交叉概率值Pc1=0.45。

變異算子：在變異過程中也采用動態變異概率，設定迭代初期的變異概率值Pm0=0.01，在迭代后期使用較小的變異概率值Pm1=0.001。

（3）算法終止條件

當滿足以下兩種搜索終止條件的其中一種，則搜索終止：（1）達到最優解連續不變最大代數C；（2）達到遺傳操作的終止代數T。

3.2 算法求解流程圖

按照上述步驟，設計主函數流程圖如圖1所示。

圖1 主函數流程圖

4 算例分析

本文采用IEEE33節點配電系統進行測試，網絡結構圖如圖2所示。假設要在此配電網中建設2個分布式電源，網絡中分布式電源待選安裝節點編號為2—33，待選單個分布式電源的功率因數取0.9，容量是0.01MVA的整數倍，分布式電源的總裝機容量不得超過最大負荷總量的10%，且小于等于所安裝節點的負荷量。參數選取如下：種群規模M=30，交叉、變異概率如3.1中所述，年最大負荷利用小時數τj=3000h，單位電價Ce=0.5元/kWh，最優解連續不變最大代數C=5，遺傳操作終止代數T=50。

圖2 IEEE33節點配電網系統圖

取目標函數中的權重系數λ1=0.8，λ2=0.2，遺傳操作過程輸出的迭代收斂曲線如圖3所示（圖中紅色線表示種群的平均適應度值，黑色線表示最佳適應度值）。

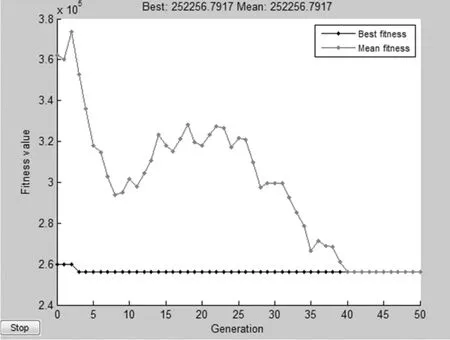
圖3 遺傳算法迭代曲線

遺傳操作后得到的分布式電源位置和容量信息見表1。

表1 DG接入節點

對接入分布式電源與不接入分布式電源的系統費用進行比較，結果見表2。

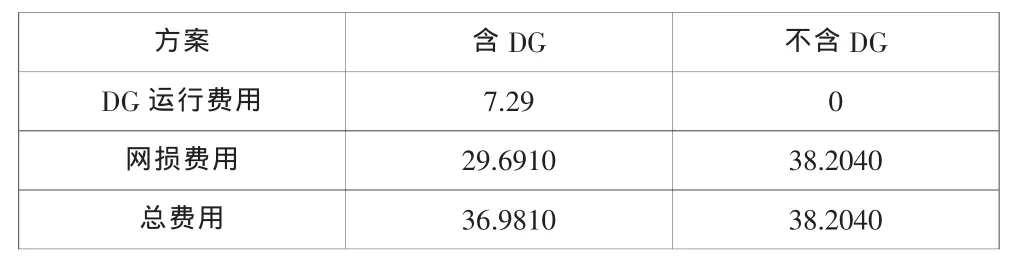
表2 接入DG與不接入DG費用比較

由以上所得的表1和表2可以看出，含DG的配電網總費用低于不含DG配網的總費用，說明僅考慮DG運行費用和網損費用的情況下，按此方案在這個配電網中接入分布式電源后系統的經濟性較好。對接入分布式電源的配電網，網損費用比不接入分布式電源的配電網低，其主要原因是分布式電源接入電網后改善了配電網的潮流分布，從而使系統網損減少。

從圖3中的遺傳算法迭代曲線可以看出，使用遺傳算法對本文目標函數進行優化，種群平均適應度值雖然局部波動比較大，但整體呈下降收斂趨勢，表明應用遺傳算法對本文目標函數進行優化取得了比較好的效果。

5 結束語

本文應用遺傳算法對配電網中分布式電源的選址與定容進行優化，以配電網的最小網絡損耗費用，分布式電源的運行費用最小為優化目標，并通過以IEEE33節點配電網系統為算例，驗證了通過遺傳算法優化DG選址與定容方案，可以有效降低系統網損，提高分布式電源帶來的經濟效益。

［1］唐小波，徐青山，唐國慶.基于“負荷質心”的分布式電源并網優化配置[J].電力自動化設備，2011，31（2）：12-16.

［2］陳琳，鐘金，倪以信，等.聯網分布式發電系統規劃運行研究[J].電力系統自動化，2007,31（9）：26-31.

［3］鄭漳華，艾芊，顧承紅，等.考慮環境因素的分布式發電多目標優化配置[J].中國電機工程學報，2009,29（13）：23-28.

［4］范明天.配電網絡規劃與設計[M].北京：中國電力出版社，1999.

［5］張立梅，唐巍.計及分布式電源的配電網前推回代潮流計算[J].電工技術學報，2010,25（8）：123-130.

［6］王成山，陳愷，謝瑩華，鄭海峰.配電網擴展規劃中分布式電源的選址和定容[J].電力系統自動化，2006，30（3）：38-43.