重視《偏微分方程》課程

劉 倩

（武漢理工大學，湖北 武漢 430070）

1 《偏微分方程》課程的重要性和特點

在自然科學和實際工程問題中的大量數學模型都可以用偏微分方程來描述，很多重要的物理、力學等學科的基本方程本身就是偏微分方程。早在微積分理論剛成立后不久，人們就開始用偏微分方程來描述、解釋或預見各種自然現象，并將所得到的的研究方法和研究成果運用于各門科學和工程技術中，不斷地取得了顯著的成效，顯示了偏微分方程對人類認識自然界基本規律的重要性。逐漸地，以物理、力學等各門學科中的實際問題為背景的偏微分方程的研究成為應用數學中的一個重要的內容，它直接聯系著眾多自然現象和實際問題，不斷地提出和產生出需要解決的新課題和新方法，不斷地促進著許多相關數學分支（如泛函分析、微分幾何、計算數學等）的發展，并從它們之中引進許多有力的解決問題的工具。偏微分方程已經成為當代數學中的一個重要的組成部分，是純粹數學的許多分支和自然科學及工程技術等領域之間的一座重要的橋梁。

2 《偏微分方程》在學習中的幾個重點和方法

2.1 以學生為中心

對于這一點是站在教師教學的角度上提出的，現如今的課堂教學中，學生是學習中的主體，而教師是引導者。要達到以學生為中心的教學目的，就必須首先在教材額內容上做到以學生為中心，充分體現并滿足學生對這門課程的需求。目前，教學內容與學生的專業特點結合的仍不夠緊密，讓學生感覺不到這門課程有很強的應用背景。結合《偏微分方程》這門課程的特點，需要在教材中適當融入一些有實際背景的案例。這樣可以方便學生借鑒，縮小教材和實際的差距，達到服務學生的目的。對于這些有實際背景的問題，是比較容易理解甚至非常熟悉，如果有意識地引導學生從這些實際問題中提出各種各樣的問題，讓學生主動去尋求解決問題的途徑，就能使學生把被動的學習方式轉化為主動的學習方式。在這里，分組討論共同一個問題或知識點，不失為一種有效的教學手段。

2.2 建立有效的學習方法

對于小組討論的問題，要積極主動去查閱各種資料，先發現問題，然后解決問題。以自身為例，我們小組討論的問題是推導弦振動方程。最先拿到教材上推導過程，基本上看不懂，然后就不得不翻閱其他參考書，才慢慢弄明白。弦振動是一種機械運動，當然機械運動的基本定律是質點力學的F=ma，但是弦并不是質點，所以質點力學的定律并不適用在弦振動的研究上，然而，如果把弦細細地分成若干個極小極小的小段，每一小段抽象地看做是一個質點，這樣就可以應用質點力學的基本定律了。

2.3 選擇合適的教學方法

要對我們學生進行啟發和引導，把背景的提出與問題的解決相結合。在進行課堂教學時，以講解式和啟發式相結合采取類比法、提問題等教學法，引導我們學生從實際北京出發，建立相應的數學模型，在對模型的分析和掌握中自然地得到解決問題的方法。例如在我們講解弦振動方程時，老師曾經讓我們思考這樣的問題：給定一根兩端固定的拉緊的均勻柔軟的弦，在外力作用下在平衡位置附近作微小的橫振動，求弦上各點的規律。首先建立直角坐標系，假設u（x，t）表示弦上各點在t時刻沿垂直于x方向的位移，弦上單位長度所受外力為F（x，t）。引導我們用所學的微積分的思想及相應的物理知識對此問題建模，可得：

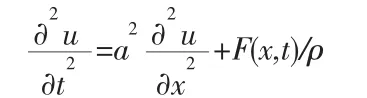
其中ρ為弦的密度。模型建立后，老師給我們介紹這就是一維的波動方程。我們認識了一維波動方程后，老師再提出問題：類似的薄膜振動、聲波的傳播等可以用波動方程來描述嗎？如果能，是什么樣的波動方程？從而引出二維波動方程、三維波動方程，同時也給我們布置了新的小組討論任務，促進我們主動學習。

注重課堂氣氛的培養，與學生形成互動。在教學中，老師可以從相關資料上收集最新的學科信息，尋找一些與《偏微分方程》相關的實用性較強的題目，在課堂上引導我們積極思考，自由討論解決問題，還可以在討論之后提出新問題。這樣既能激發我們學習的興趣，又能使我們對課堂內容實踐化，培養其解決實際問題的能力。

數學物理方程的講授多采用傳統的板演方式，這種方式，公式推導直觀，學生容易理解；但由于推導過程長，我們往往容易迷失于密密麻麻的板書中。但如果全部用多媒體來進行教學的話，由于信息量大和過程跨度大，我們往往對公式的推導理解困難，也收不到良好的教學效果。鑒于此，以傳統的教學方式為主，不時輔以多媒體教學。在重難點處仍然使用傳統的板演，給我們更多思考的空間和時間，既突出了重點，又借助良好的互動使我們的理解更加透徹。

這樣，通過運用現代教學技術，增加實踐環節，培養了我們掌握知識和解決問題的能力，提高了我們的學習熱情和興趣，同時也創造了良好的學習氛圍，最終收到很好的學習效果。

［1］湯燕斌,吳娥子.應用偏微分方程[M].北京：科學出版社,2010.

［2］谷超豪.數學物理方程[M].北京：高等教育出版社,2002.

［3］梁昆淼.數學物理方法[M].4 版.北京：高等教育出版社,2010.

［4］陳軍斌,等.創新教學方法提高研究生《數理方程與數值解》課程教學質量[J].2011(9)：33.

［5］林家翹,西格爾 LA.自然科學中確定性問題的應用數學[M].趙國英，等,譯.北京：科學出版社,2010.