Runge－Kutta Multi－resolution Time－Domain Method for Modeling 3DDielectric Curved Objects

Zhu Min（朱敏），Cao Qunsheng（曹群生）＊，Zhao Lei（趙磊），Wang Yi（王毅）

1.College of Electronic and Information Engineering，Nanjing University of Aeronautics and

Astronautics，Nanjing，210016，P.R.China；2.Nanjing ASSEN Environment Technology Co.Ltd.，Nanjing，210000，P.R.China

1 Introduction

The finite－difference time－domain（FDTD）method has been widely used in the field of computational electromagnetics due to its simple implementation and a capability to address complex targets［1］.It is known that the FDTD method has two primary drawbacks.One is that the numerical dispersion is the dominate limitation to the accuracy of the FDTD method.The other is that it is not able to accurately model curved surfaces and material discontinuities by using the stair－casing approach with structured grids.In the past decades，numerous efforts have been made to improve the traditional FDTD method such as the high－order methods.The multi－resolution timedomain（MRTD）method has been proposed to improve numerical dispersion properties［2－6］.The Runge－Kutta multi－resolution time－domain（RKMRTD）has been proposed by Cao［7－8］to improve the dispersion and convergence in both time and spatial domains.However，these methods also have shortcomings to deal with curved objects.The conformal FDTD technique is one of candidates to circumvent this problem.Nowadays，more attentions are focused on how to modeling curved objects.Locally conformal FDTD（CFDTD）method was proposed by Dey，et al［9］to accurately model the curved metallic objects，and it is more accurate than the FDTD method.Stefan，et al［10］proposed a new conformal perfect electric conductor（PEC）algorithm，of the FDTD method，which only needed to change two fieldupdated coefficients.It could privilege either speed or accuracy when choosing a time step reduction.Some other papers investigated how to accurately model curved dielectric objects using the CFDTD method［11－13］.

However，few papers discuss the conformal RK－MRTD（C－RKMRTD）method to deal with the curved dielectric objects.In this paper，the CRKMRTD method is derived and presented.Besides，numerical examples are also given to verify the proposed method［14］.

2 C－RKMRTD Method

2.1 RK－MRTD method

For simplicity（σ＝0）and without loss of generality，in three－dimensional（3D）one of the RK－MRTD［7］update equations can be written as

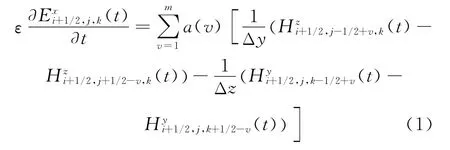
where mis the spatial stencil size.Parametersε，Δt，Δx，Δy，andΔzare the permittivity，temporal step size，and spatial step sizes along x－，yand z－directions，respectively.The coefficients a（v）is the same as defined in Ref.［7］.

2.2 C－RKMRTD method

In order to derive the general update equations of the C－RKMRTD method with the spatial step sizeΔx＝Δy＝Δz，Eq.（1）can be rewritten in another form as

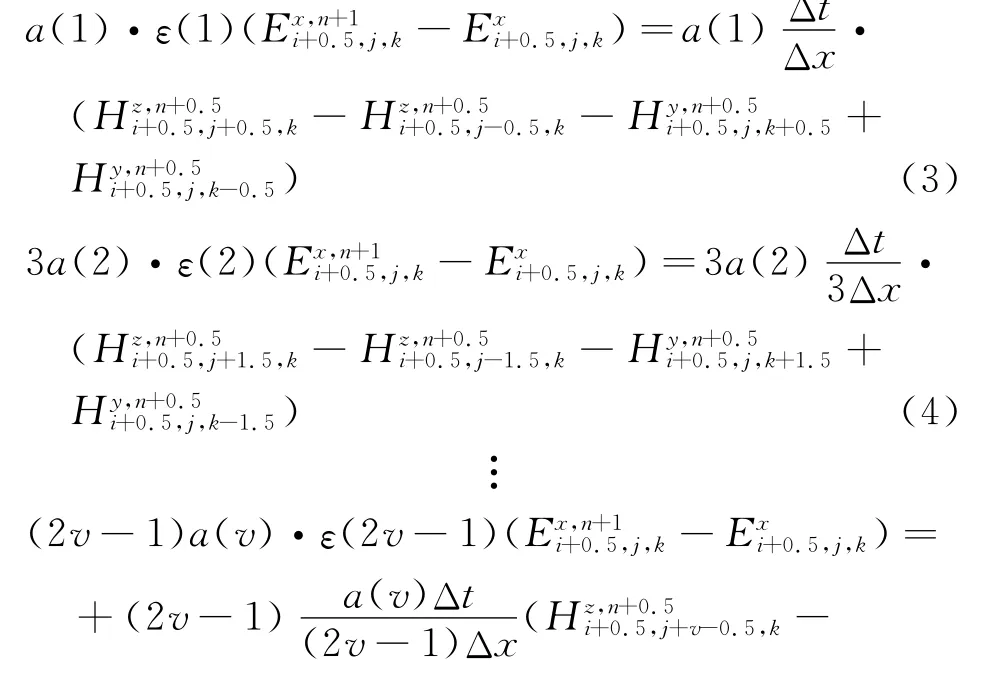
where coefficientsε（v）（v＝1，2，…，2v－1）are the permittivities corresponding to the cell sizeΔx，3Δx，…，and（2v－1）Δx，respectively.It is clear that for a givenΔx，Eqs.（4，5）can thus be treated as the intervals 3Δxand（2v－1）Δxin the FDTD update equations.The multi－region decomposition of electric field Eis shown in Fig.1.

Fig.1 Efield multi－region decomposition for conformal high－order FDTD method

Adding Eqs.（2－5），the update equation of the C－RKMRTD method is expressed as

From Eq.（6），it is easy to see that the update equation of C－RKMRTD method is constituted by（2v－1）normal FDTD method with cell sizes ofΔx，3Δx，…，（2v－1）Δx.

Comparing Eqs.（1）and（6），it is clearly found that the effective dielectric constantεeffis

The weighting area［15］is used to obtainε（v）as

Three different conditions for the objects interface are shown in Fig.2.

3 Numerical Experiments

Fig.2 Different conditions for curved object interface

The numerical simulations are presented to validate the C－RKMRTD method.The two simu－lations both take 10cells per wavelength.The number of Courant，Friedrichs，Lewy（CFL）is 0.3，and an eight－layer of anistropic perfectly matched layer（APML）is used to truncate the computational domain.All computational simulations are based on a computer of Pentium with a dual－core 2.8GHz CPU and 1.87Gmemory.

3.1 Dielectric cylinder

The dielectric cylinder with a radius of 0.06m，height of 0.015m，the relative permittivityεrof 4，and relative permeabilityμrof 1.0.The cylinder is illuminated by an incident plane wave coming from the z－direction with a polarization in the x－direction at 10GHz.The total computational volume is discretized into 82×82×82 cells.The bistatic radar cross sections（RCSs）in E－plane obtained from different methods，i.e.，method of moments（MoM），MRTD and C－RKMRTD，are shown in Fig.3，whereθis the incident angle.The C－RKMRTD method agrees with the MoM method better than the MRTD method.Table 1lists the magnitudes of the spatial discretization，temporal discretization，total computational domain，total time steps and CPU time.Fig.4shows the difference between the C－RKMRTD／MRTD and the MoM method.

Fig.3 Bistatic RCS in E－plane of the dielectric cylinder obtained by different methods

Table 1 Comparison for different methods

Fig.4 Difference between C－RKMRTD（MRTD）and MoM method

3.2 Dielectric ellipsoid

The structure of dielectric ellipsoid with the radii of 0.6，0.6and 0.3min the x－，y－，z－directions，respectively.The relative permittivity εris 4，the relative permeabilityμris 1，the polarization of the electric field is in the x－direction，and the wavelength is 0.3m.

Backward scattering bistatic RCSs obtained by different methods are shown in Figs.5，6.It is found that the results of C－RKMRTD method is consistent with those of the MoM method and its performance is better than that of the non－conformal methods.The comparisons of the computational cost of different methods are displayed in Table 2.Fig.7shows the difference between C－RKMRTD／MRTD and the MoM methods.Fig.8 shows the difference between C－RKMRTD／FDTD and the MoM method.

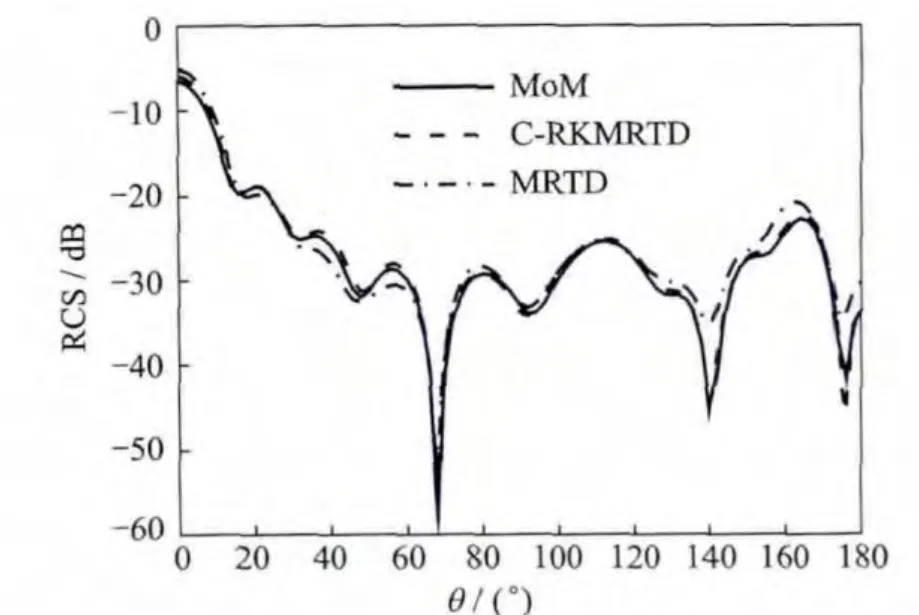
Fig.5 Dielectric RCS in E－plane of the ellipsoid obtained by different methods

Fig.6 Bistatic RCS in H－plane of the dielectric ellipsoid using different methods

Table 2 Comparison for different methods

Fig.7 Difference between C－RKMRTD／MRTD and MoM method

Fig.8 Difference between FDTD／C－RKMRTD and the MoM method

4 Conclusion

An efficient approach that combines the conformal technique and RK－MRTD method is implemented to model the curved objects for the scattering problems.Numerical results demonstrate the higher accuracy and efficiency of the proposed method，compared with non－conformal methods including the MRTD and FDTD methods.

［1］ Yee K S.Numerical solution of initial boundary value problems involving Maxwell′s equations in isotropic media［J］.IEEE Trans Antennas Propagat，1966，AP－14：302－307.

［2］ Krumpholz M，Katehi L P B.MRTD：New time－domain schemes based on multiresolution analysis［J］.IEEE Trans Microw Theory Tech，1996，44：555－571.

［3］ Tentzeris E M，Robertson R L，Harvey J F，et al.Stability and dispersion analysis of battle－Lemariebased MRTD schemes［J］.IEEE Trans Microw Theory Tech，1999，47（7）：1004－1013.

［4］ Dogaru T，Carin L.Multiresolution time－domain using CDF biorthogonal wavelets［J］.IEEE Trans Microw Theory Tech，2001，49（5）：3902－3912.

［5］ Fujii M，Hoefer W J R.Dispersion of time－domain wavelet Galerkin method based on Daubechies compactly supported scaling functions with three and four vanishing moments［J］.IEEE Microwave and Guided Wave Letters，2002，10（7）：1752－1760.

［6］ Zhu X，Dogaru T，Carin L.Three－dimensional biorthogonal multiresolution time－domain method and its application to scattering problems［J］.IEEE Trans Microw Theory Tech，2003，51（5）：1085－1092.

［7］ Cao Q，Kanapady R，Reitich F.High－order Runge－Kutta multiresolution time－domain methods for computational electromagnetics［J］.IEEE Trans Microw Theory Tech，2006，54（8）：3316－3326.

［8］ Zhu Min，Cao Qunsheng.Studying and Analysis of the Characteristic of the High－Order and MRTD and RK－MRTD Scheme［J］.Applied Computational Electromagnetics Society，2013，28（5）：380－389.

［9］ Dey S，Mittra R.A locally conformal finite－difference time－domain（FDTD）algorithm for modeling three－dimensional perfectly conducting objects［J］.IEEE Microwave and Guided Wave Letters，1997，7（9）：273－275.

［10］Stefan B，Nicolas C.A new 3－D conformal PEC FDTD scheme with user－defined geometric precision and derived stability criterion［J］.IEEE Trans Antennas Propagat，2006，54（6）：1843－1849.

［11］Yu Wenhua，Mittra R.A conformal finite difference time domain technique for modeing curved dielectric surfaces［J］.IEEE Microwave Wireless Components Letter，2008，11（1）：25－27.

［12］Wang J，Yin W Y.FDTD（2，4）－compatible conformal technique for treatment of dielectric surfaces［J］.Electronic Letters，2009，45（3）：146－147.

［13］Daubechies I.Ten lectures on wavelets［M］.PA：SIAM，1992.

［14］Zhu M，Cao Q，Wang Y.Conformal multi－resolution time－domain method for scattering curved dielectric objects［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2014，31（3）：269－273.

［15］Wang Jian，Yin Wenyan.Development of a novel FDTD（2，4）－compatible conformal scheme for electromagnetic computations of complex curved PEC objects［J］.IEEE Trans Antennas Propagat，2013，61（1）：299－309.