女裝涼鞋質量檢測項目示值的測量結果不確定度
胡 昆
(惠州市質量計量監督檢測所,廣東 惠州 516001)
女裝涼鞋質量檢測項目示值的測量結果不確定度
胡昆
(惠州市質量計量監督檢測所,廣東惠州516001)
摘要:為提高女裝涼鞋質量項目檢測的準確性,更好分析檢測過程中的數據分析和判定,確保檢測機構對女裝涼鞋質量檢驗時,對相關檢驗結果更準確的表達和可靠性。以此例在市場上普遍大眾女裝涼鞋為例,展開相關測量結果不確定度的分析。
關鍵詞:女裝;涼鞋;不確定度
測量方法(依據GB/T22756-2008《皮涼鞋》)
根據GB/T22756-2008《皮涼鞋》,采用各檢測項目采用直接測量法。本文實驗檢測項目及選用的計量標準器。

表1-1 檢測項目及選用的標準器
綜合考慮,本不確定度主要為使用標準設備不同而帶來主要不確定度,故本文主要考慮同一標準設備使用時不確定度分析,相同標準者可參照。
1 鋼卷尺部分
1.1數字模型
設前幫示值為IX,鋼卷尺相應的讀數值為IN,則被檢儀示值的誤差可表示為:

式中:IX-前幫示值;
IN-鋼卷尺示值;
b-標準不確定度;
t-檢測溫度偏離(20±5)℃的值;
r-檢測人員操作引入不確定度;
δ-測量重復性引入不確定度;
在實驗室環境下,由溫度系數及檢測人員均有三年以上檢測經驗,持證上崗故帶來的誤差可忽略。故由式(1)得:

1.2方差和傳播系數
(2)式中IX、IN為非相關量,則得到:

1.3計算標準不確定度分量
1.3.1前幫示值測量的標準不確定度u(IX)
1.3.2標準儀器示值的分辨力的不確定度分量u(Ib)
標準儀器示值在量程為(0~3)m時的分辨力為1mm的區間內,Ib取任一值。該誤差分布屬均勻分布,覆蓋因子k=。故:

1.3.3測量重復性的不確定度u(IN3)
本實驗以前幫實測長度為檢測點為例,進行5次等精度測量,所得數據列為:31.2、31.8、32.0、31.3、32.0mm。
以上兩項各不相關,合成得:

1.4標準不確定度一覽表(如表1-2所示)

表1-2 標準不確定度一覽表
1.5合成標準不確定度

2 數顯卡尺部分
2.1數字模型
設前掌著力部位扣除花紋后厚度(簡稱前掌著力厚度)示值為IX,數顯卡尺相應的讀數值為IN,則被檢儀示值的誤差可表示為:

式中:IX-前著力厚度示值;
IN-數顯卡尺示值;
b-標準不確定度;
t-檢測溫度偏離(20±5)℃的值;
r-檢測人員操作引入不確定度;
δ-測量重復性引入不確定度;
在實驗室環境下,由溫度系數及檢測人員均有三年以上檢測經驗,持證上崗故帶來的誤差可忽略。故由式(1)得:

2.2方差和傳播系數
(2)式中IX、IN為非相關量,則得到:
傳播系數:c(Ix)=f/Ix=1;
c(IN)=f/IN=-1。
2.3計算標準不確定度分量
2.3.1 前掌著力厚度示值測量的標準不確定度u(IX)
2.3.2 標準儀器示值的分辨力的不確定度分量u(Ib)
標準儀器示值在量程為(0~150)m時的分辨力為0.01mm的區間內Ib取任一值。該誤差分布屬均勻分布,覆蓋因子k =。故:

2.3.3測量重復性的不確定度u(IN3)
本實驗以前幫實測長度為檢測點為例,進行5次等精度測量,所得數據列為:12.91、12.92、12.91、12.92、12.91mm。
以上兩項各不相關,合成得:

2.4標準不確定度一覽表(如表1-3所示)

表1-3 標準不確定度一覽表
2.5合成標準不確定度
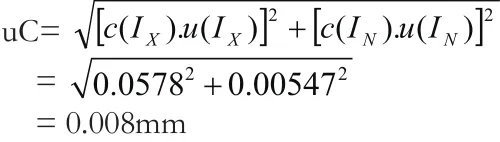
3 鋼直尺部分
3.1數字模型
設后跟示值為IX,鋼卷尺相應的讀數值為IN,則被檢儀示值的誤差可表示為:

式中:IX-后跟高度示值;
IN-鋼直尺示值;b-標準不確定度;
t-檢測溫度偏離(20±5)℃的值;
r-檢測人員操作引入不確定度;
δ-測量重復性引入不確定度;
在實驗室環境下,由溫度系數及檢測人員均有三年以上檢測經驗,持證上崗故帶來的誤差可忽略。故由式(1)得:

3.2方差和傳播系數
(2)式中IX、IN為非相關量,則得到:
傳播系數:c(Ix)=f/Ix=1;
c(IN)=f/IN=-1。
3.3計算標準不確定度分量
3.3.1后跟示值測量的標準不確定度u(IX)
3.3.2標準儀器示值的分辨力的不確定度分量u(Ib)
標準儀器示值在量程為(0~60)mm時的分辨力為1mm的區間內,Ib取任一值。該誤差分布屬均勻分布,覆蓋因子k=。故:
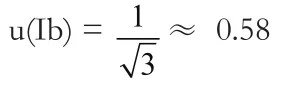
3.3.3測量重復性的不確定度u(IN3)
本實驗以后跟實測長度為檢測點為例,進行5次等精度測量,所得數據列為:68.0、68.5、68.0、68.5、68.0mm。
依據貝塞爾公式,得:

3.4標準不確定度一覽表(如表1-4所示)

表1-4 標準不確定度一覽表
3.5合成標準不確定度

4 邵爾硬度部分
4.1數字模型(邵爾硬度部分)
設跟底示值為IX,鋼卷尺相應的讀數值為IN,則被檢儀示值的誤差可表示為:

式中:IX-后跟高度示值;
IN-鋼直尺示值;
b-標準不確定度;
t-檢測溫度偏離(20±2)℃的值;
r-檢測人員操作引入不確定度;
δ-測量重復性引入不確定度;
在實驗室環境下,由溫度系數及檢測人員均有三年以上檢測經驗,持證上崗故帶來的誤差可忽略。故由式(1)得:

4.2方差和傳播系數
依照方差公式:

(2)式中IX、IN為非相關量,則得到:

4.3.1跟底示值測量的標準不確定度u(IX)
4.3.2標準儀器示值的分辨力的不確定度分量u(Ib)
標準儀器示值在量程為(0~100)d時的分辨力為1d的區間內,Ib取任一值。該誤差分布屬均勻分布,覆蓋因子k=。故:

4.3.3測量重復性的不確定度u(IN3)
本實驗以跟底實測檢測點為例,進行5次等精度測量,所得數據列為:98.2、99.0、98.5、98.5、99.0d。

4.4標準不確定度一覽表(如表1-5所示)
以上兩項各不相關,合成得:

表1-5 標準不確定度一覽表
4.5合成標準不確定度:

5 拉力部分
5.1數字模型
設鞋幫示值為IX,拉力機相應的讀數值為IN,則被檢儀示值的誤差可表示為:
IX=IN+(b+t+r+δ)(1)
式中:IX-鞋幫拉出強度示值;
IN-拉力機示值;
b-標準不確定度;
t-檢測溫度偏離(20±2)℃C的值;
r-檢測人員操作引入不確定度;
δ-測量重復性引入不確定度;
在實驗室環境下,由溫度系數及檢測人員均有三年以上檢測經驗,持證上崗故帶來的誤差可忽略。故由式(1)得:
△=IX-IN(2)
5.2方差和傳播系數
式中IX、IN為非相關量,則得到:
5.3計算標準不確定度分量
5.3.1鞋幫示值測量的標準不確定度u(IX)
5.3.2標準儀器示值的分辨力的不確定度分量u(Ib)
標準儀器示值在量程為(0~5000)N,1級合格的區間內,Ib取任一值。該誤差分布屬均勻分布,覆蓋因子k=;。本次檢測帶來分量為1%,轉為量程絕對量,100N范圍內為1N
5.3.3測量重復性的不確定度u(IN3)
本實驗以前幫實測長度為檢測點為例,進行5次等精度測量,所得數據列為:87.11、87.32、88.23、88.14、87.68N。
以上兩項各不相關,合成得:

5.4標準不確定度一覽表(如表1-6所示)

表1-6 標準不確定度一覽表
5.5合成標準不確定度:

綜合以上分析,本站標準設備各不確定度為如表
參考文獻:
[1]戚曉霞,張偉娟.皮涼鞋,中國標準出版社[S].GB/T22756-2008.
[2]葉德培,原遵東等.測量不確定度評定與表示[S].中國質檢出版社.JJF1059.1-2012、JJF1059.2-2012.

