列車誘發振動對轉體施工橋梁穩定性影響分析

高 日，胡志波，高 濤，孟 兮

(北京交通大學土木建筑工程學院，北京 100044)

隨著我國交通事業的發展，上跨既有鐵路、公路的橋梁工程日漸增多，橋梁轉體施工方法越來越多地運用到城市軌道交通建設中。橋梁轉體施工是指將橋梁轉體結構在非設計軸線位置制作成型后，利用預設的球鉸等轉動設備將橋梁轉動到設計軸線上的一種施工方法。它可以將在障礙上空的作業轉化為岸上或近地面的作業。根據橋梁結構的轉動方向，轉體施工可以分為豎轉法、平轉法以及平轉和豎轉相結合的方法，其中以平轉法應用最多［1-2］。

平轉法施工通常應用在跨越鐵路的轉體橋中。這種施工方法無需在鐵路線側搭設支架，能最大限度地減少對列車正常通行產生的干擾，經濟效益和社會效益十分明顯。由于轉體橋是在鐵路線附近施工，轉體梁脫架后或平衡轉體過程中將會不可避免地受到列車誘發的地面振動的影響。列車通過時誘發的振動通過球鉸傳遞到巨大的懸臂轉體梁上，將會對梁體的受力產生一定影響。按照一般的處理方法，這種振動可以等效為一次有感知的地震波的輸入。這種振動能否影響轉體橋梁的整體安全，目前還沒有文獻對此進行過分析。因此，有必要開展這一方面的試驗研究工作，為類似轉體施工橋梁的設計、施工及運營管理積累經驗和數據。

1 工程實例的選擇及工程概況

秦皇島市西部快速路工程跨越京哈鐵路采用轉體施工橋梁。該橋主橋為雙幅獨立式橋，處在直線段上，每幅橋寬23.0 m，全寬47.5 m。轉體部分為2×42 m。上部結構采用預應力混凝土單箱四室箱梁。下部結構主橋轉體墩采用空心矩形墩柱，下接轉體平臺。轉體平臺支撐在承臺上，采用鉆孔灌注樁基礎。轉盤結構采用環道與中心支承相結合的球鉸轉動體系，球鉸球面半徑為6.048 m。該轉體橋轉動角度為73.3°，每幅梁的轉體質量達7 200 t。轉體橋沿鐵路平面布置圖如圖1所示。

該橋梁在轉體施工前已經完成了稱重和配重試驗。由試驗測得北側橋梁的縱向球鉸摩阻力矩為5 995 kN·m，不平衡力矩為16 650 kN·m，摩阻系數為0.015，橋梁偏向東側，選擇的配重方案為在東側取下15 t掛板。南側橋梁縱向球鉸摩阻力矩為10 124 kN·m，不平衡力矩為8 761.8 kN·m，摩阻系數為0.025，橋梁偏向西側。由于該側橋梁的偏心距已滿足5～15 cm的經驗要求，沒有進行配重。造成兩側轉體摩阻力矩相差較大的主要原因是施工誤差。

2 測量時程曲線

本次研究將列車誘發的地面振動等效為地震荷載。目前在工程上求解地震反應的方法分為兩類:一類是擬靜力法，另一類為時程分析法［3-4］。通過時程分析可以得到各質點隨時間變化的位移、速度和加速度動力反應，并且可以進一步計算出結構的內力時程變化，同時時程分析法能夠比較真實地、合理地模擬機構的地震響應［5］。鑒于轉體橋的特點和時程分析的優點，本次研究采用時程分析法。利用加速度傳感器對球鉸附近地面振動情況進行測試，記錄每次列車通過時的縱向、橫向及豎向加速度時程曲線。表1是本次試驗每組數據的列車類型和行駛方向，其中上行是指列車開往北戴河方向，下行是指列車開往南戴河方向。本次研究對15趟列車通過時轉體橋球鉸處的地基振動數據進行了記錄。

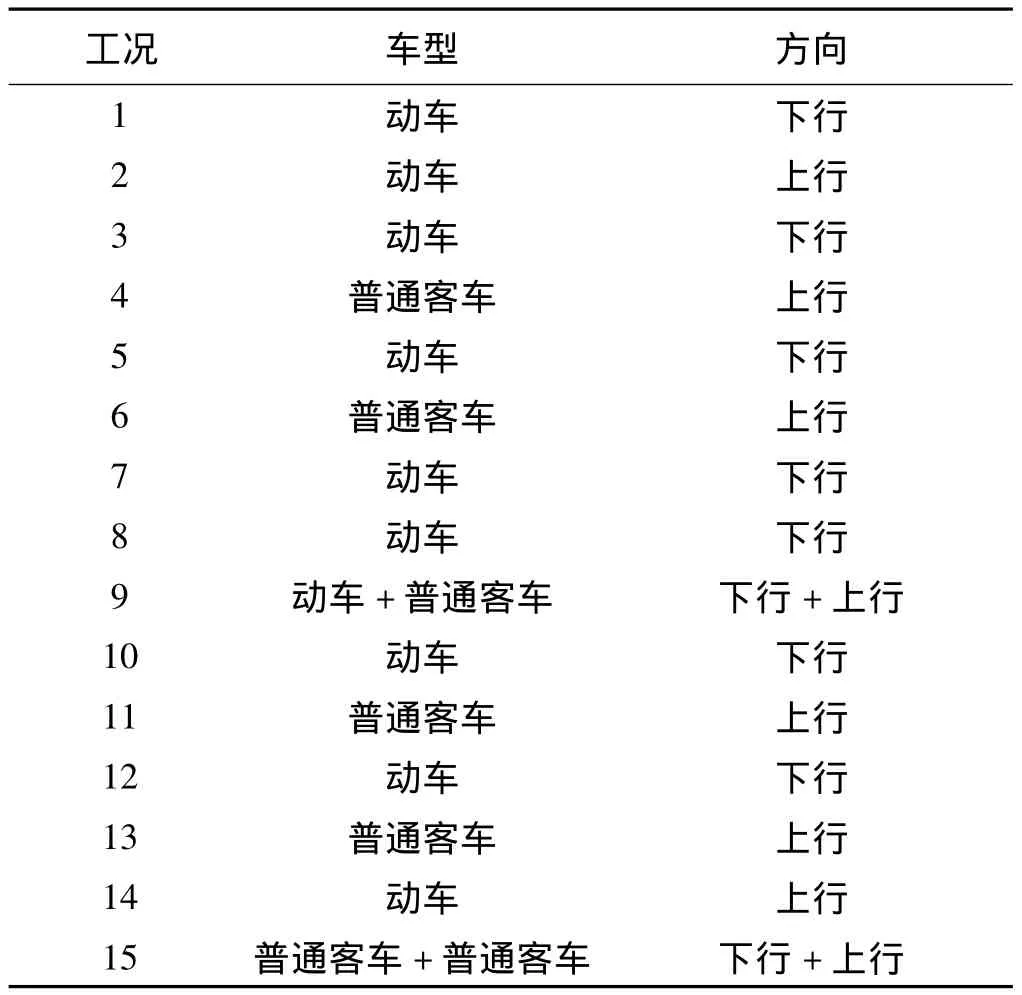
表1 列車通過時振動測試記錄

圖2為地面測點平面布置圖。數據采集系統的采樣頻率為200 Hz。

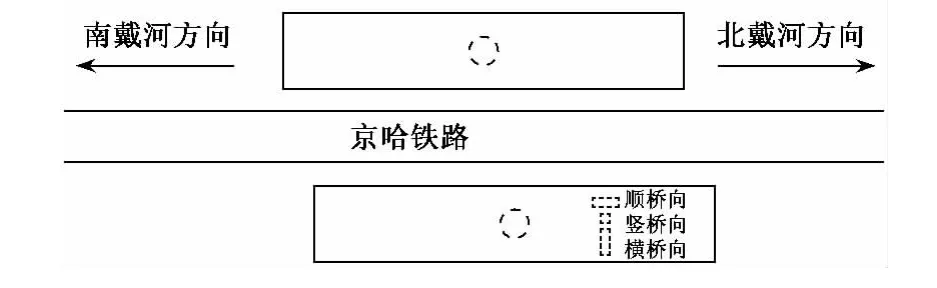
圖2 地面測點平面布置

3 梁體穩定性評估

3.1 轉體梁振動分析

評估列車誘發地面振動對梁體穩定性的影響時采用有限元分析法。在Midas中建立橋梁的有限元模型，采用梁單元，每幅橋共分為84個單元，85個節點，球鉸簡化為固定支座，模型如圖3所示。

圖3 轉體橋有限元模型

輸入每一趟列車通過時實測的加速度時程曲線，進行振動響應分析。表2～表4分別是具有代表性的客車(工況6)、動車(工況1)以及京哈兩方向列車(工況9)分析結果。

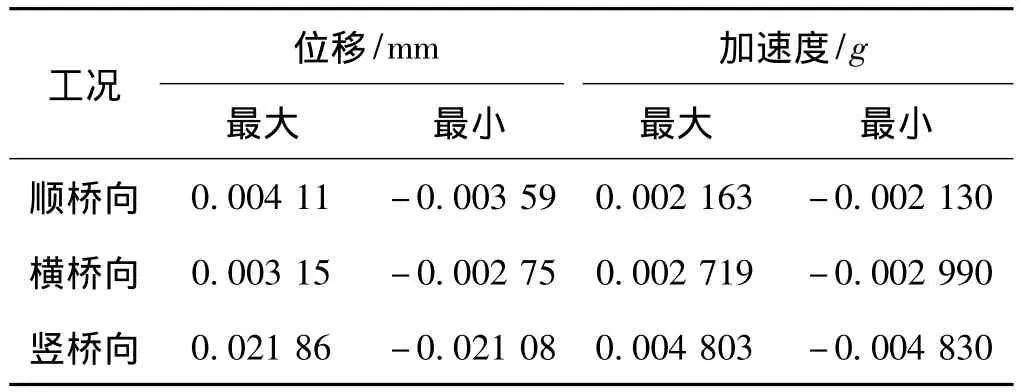
表2 客車通過時轉體梁振動分析結果

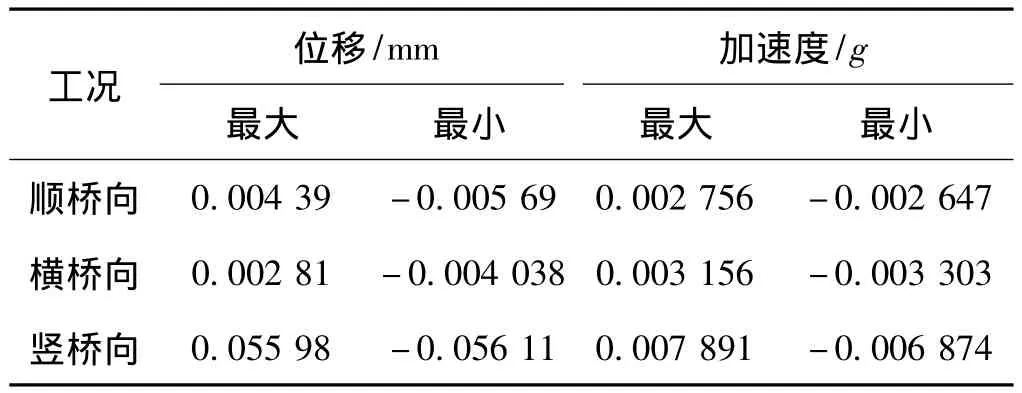
表3 動車通過時轉體梁振動分析結果

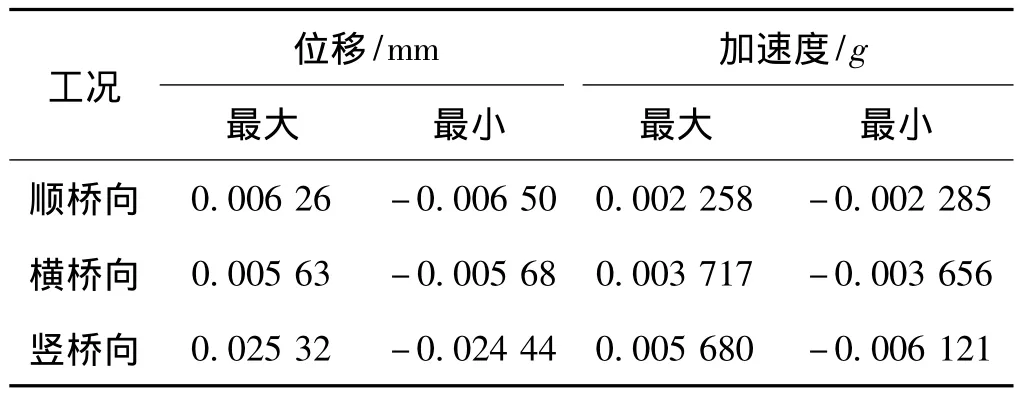
表4 京哈兩方向列車同時通過時轉體梁振動分析結果

由表2～表4可知，無論是橫向、縱向還是豎向，其各點最大加速度都很小，均不超過0.1g。各個方向上的最大、最小位移也很小。由此可知列車誘發的地面振動不會使梁體產生明顯的振動。

3.2 球鉸轉動力矩分析

結構或構件傾覆的條件為傾覆力矩大于抗傾覆力矩。對本轉體橋進行如圖4(a)所示的簡化。針對稱重和配重后得到的數據，考慮最不利情況，即不平衡力矩與振動產生的轉動力矩同向，此時轉體橋發生傾覆的條件為

式中:MG為橋梁不平衡力矩，是球鉸兩側橋梁對球鉸中心產生的力矩差值;M為外部作用對轉體橋產生的力矩，此處為列車振動所產生的力矩;MC為撐腳對球鉸中心產生的力矩，此處假定一個撐腳與承臺接觸;MZ為球鉸摩阻力矩。

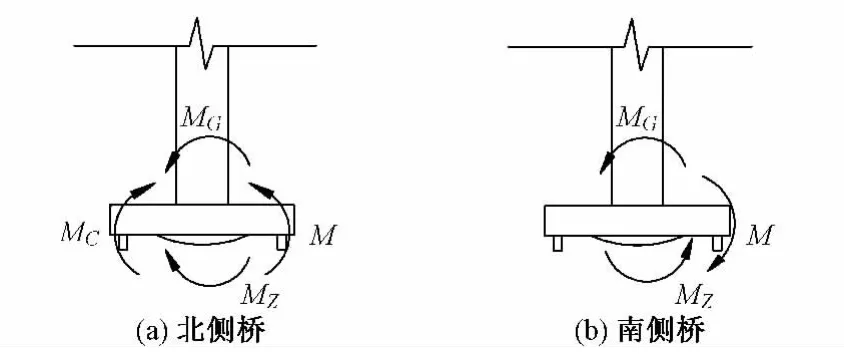
圖4 轉體梁受力分析

通過計算分析后可得北側轉體橋配重后橋梁的不平衡力矩為14 886 kN·m;南側轉體橋沒有進行配重，橋梁不平衡力矩為8 761.8 kN·m。北側梁的摩阻力矩小于南側梁的摩阻力矩，且北側橋梁的不平衡力矩大于南側橋梁的不平衡力矩。在列車振動導致的球鉸轉動力矩分析中，取摩阻力矩較小的北側梁球鉸進行分析。

對表1中的時程記錄利用Midas進行有限元分析，得到列車振動引起的最大轉動力矩，見表5。

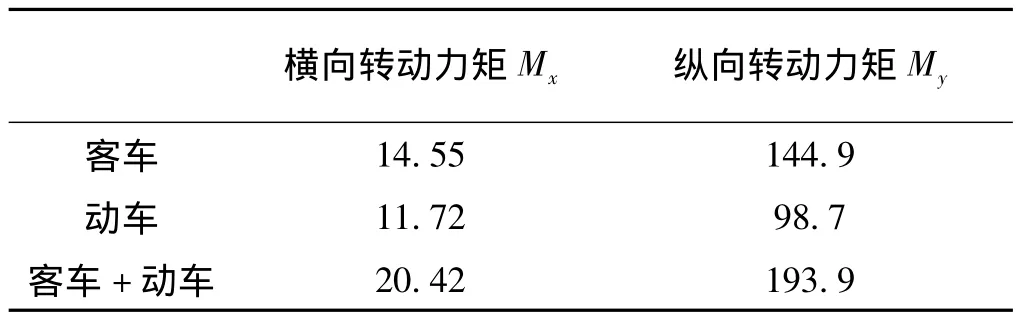
表5 列車振動引起的球鉸最大轉動力矩 kN·m

撐腳所能提供的最大力矩MC的計算可采用下列各式［6］

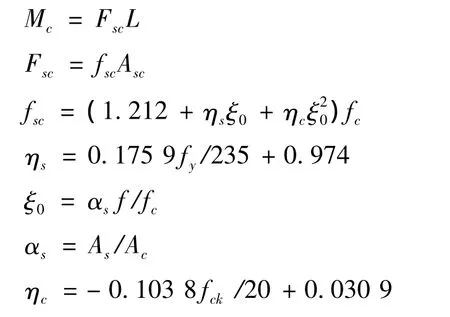
式中:fsc為鋼管混凝土的組合軸壓比強度設計值;fck，fc分別為混凝土的軸心抗壓強度標準值和設計值;f為鋼材的抗拉、抗壓和抗彎強度設計值;fy為鋼材的屈服強度;ξ0為構件截面含鋼率;As，Ac分別為鋼管和混凝土的截面面積;ηs，ηc分別為計算系數;Asc為鋼管混凝土的截面面積;Fsc為鋼管混凝土的壓力設計值。

通過上式求得Mc為350 072 kN·m。代入數據可知MC+MZ＞＞MG+M。因此在橋梁轉動前及轉動過程中，即使有列車通過，梁體也不會發生傾覆。

進一步對梁體由于列車誘發的地面振動而產生的晃動情況進行分析。由記錄的加速度時程曲線可知，加速度的方向隨著時間在不斷變化。在這種變化過程中對球鉸產生的縱向轉動力矩若足夠大，即滿足M＞MG+MZ的條件，此時梁體就會發生晃動。取最不利的南側轉體橋進行受力分析，參見圖4(b)。通過同樣的模擬及計算可知MZ+MG＞＞M。因此在轉體過程中，即使在有列車通過的情況下，球鉸不會發生轉動，梁體也不會發生晃動。

4 結論

1)列車誘發的振動不會對該轉體橋的穩定性產生很大的影響。梁體各點振動位移和加速度遠小于本地區抗震設防烈度值。

2)該梁體不會由于列車誘發的地面振動而晃動，更不會傾覆。

3)該橋在轉體施工過程中可以不封閉所要跨越的鐵路。

4)其它類似橋梁可采用同樣的分析方法，以評估列車誘發振動對轉體橋穩定性的影響，決定是否封閉交通。

［1］張健峰，鐘啟賓.橋梁水平轉體法施工的技術成就及發展［J］.鐵道標準設計，1992(6):19-41.

［2］張聯燕.橋梁轉體施工［M］.北京:人民交通出版社，2003:1-9.

［3］范立礎，卓衛東.橋梁延性抗震設計［M］.北京:人民交通出版社，2001.

［4］范立礎.橋梁抗震［M］.上海:同濟大學出版社，2007.

［5］郁中偉，馬良，鄭明玉.現行橋梁抗震理論與設計方法［J］.山西建筑，2008(1):313-314.

［6］中華人民共和國國家經濟貿易委員會.DL/T 5085—1999鋼—混凝土組合結構設計規程［S］.北京:中國電力出版社，1999.