一維無界域上Burgers方程的局部人工邊界條件

周道，金繼承

（湖南工業大學理學院，湖南株洲412007）

一維無界域上Burgers方程的局部人工邊界條件

周道，金繼承

（湖南工業大學理學院，湖南株洲412007）

針對無界域上的一維Burgers方程，首先運用Cole-Hopf函數變換，將非線性Burgers方程變換成線性的熱傳導方程；再通過Padé逼近得到局部的人工邊界條件；最后，對得到的非線性初邊值問題進行有限差分離散。數值實驗表明，提出的人工邊界條件是恰當的，并且是有效的。

Burgers方程；人工邊界條件；有限差分方法；Pad逼近

1 背景知識

Burgers方程是1948年J. M. Burgers[1]為描述湍流問題而首次提出。隨著研究的深入，人們發現它是對流和耗散流之間相互影響的簡單模型之一，它可以模擬湍流、激波等物理現象，它是Navier-Stokes方程的一種簡化形式，這使得它成為一個非常重要的模型方程。這類方程是非線性的，解析解求解復雜或者難以求解；而它要求在無界域上求解，使得數值方法求解也變得困難和低效。因此，研究此類方程的高效數值算法具有重要的理論和現實意義。

近20年來，針對無界域上方程的求解，一種重要的方法是構造人工邊界條件。這種方法已成功應用于許多無界域問題的求解[2-6]，本文亦采用此類方法。其他學者針對無界域上的Burgers方程也有一些研究成果：文獻[7]給出了一維情況的準確人工邊界條件，并應用差分方法進行了數值試驗；文獻[8]應用Cole-Hopf函數變換和傅里葉逼近給出了二維情況的準確人工邊界條件和一類近似人工邊界條件；文獻[9]引入了一種差分格式，給出一維Burgers方程的一類近似的人工邊界條件，并進行了收斂性分析。但是這些人工邊界條件都是非局部的。

考慮如下一維Burgers方程初值問題：

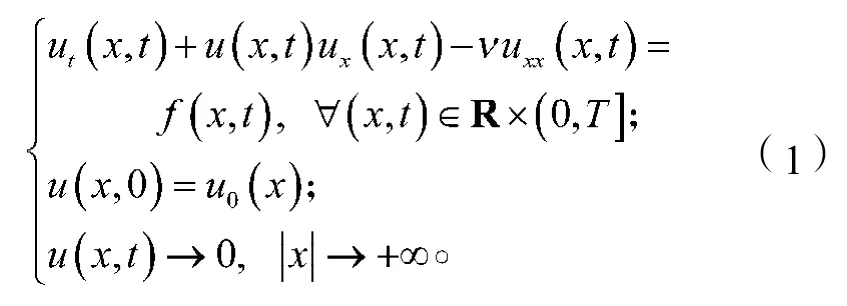
式中：v＞0是粘性系數；

f(x, t)和u0(x)分別是外界能量和初始條件，都是具有緊支集的函數，且滿足

問題（1）是一個在無界域上的問題，通常引入如下2個人工邊界：

顯然，當用差分方法對以上邊界條件進行離散時，計算當前時刻的值通常要用到之前幾乎所有時間步上的值，稱這種邊界條件為非局部的（non-local）。與之對應，如果一種邊界條件被離散時，計算未知函數當前時刻的值，只需用到之前少數幾個時間步上的值，那么稱這種邊界是局部的（local）。與非局部的人工邊界相比，局部的人工邊界條件的計算復雜程度較低，需要的存儲空間較少。

2 局部人工邊界條件的構造

考慮構造一維無界域上滿足條件（2）的Burgers方程（1）的人工邊界。

4)農村生活、分散型畜禽、種植業廢棄物污染負荷削減與資源化利用技術體系研究。三峽庫區農戶生活、分散型畜禽、種植業廢棄物等污染嚴重，可針對此情況進行農村生活垃圾分類收集、集中儲存、定期清運；分散型畜禽糞便的資源化利用技術及模式，如沼氣農業生態循環利用技術、生物廢水生物掛膜處理技術、高效安全土地處理技術、堆肥處理技術；秸稈資源綜合利用的關鍵技術及循環利用模式，如秸稈生物質氣化利用技術、秸稈碳化、膨化以及表面改性利用技術研究。

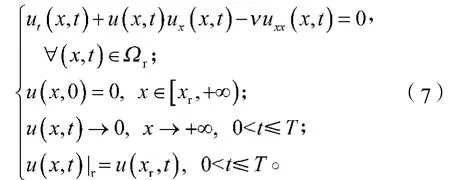
由于函數u(xr, t)是未知的，所以式（7）不能獨立求解。但如果假設邊值條件u(xr, t)是給定的，那么問題就是適定的。

下面用Cole-Hopf變換將（非線性的）Burgers方程轉化成（線性的）熱傳導方程。

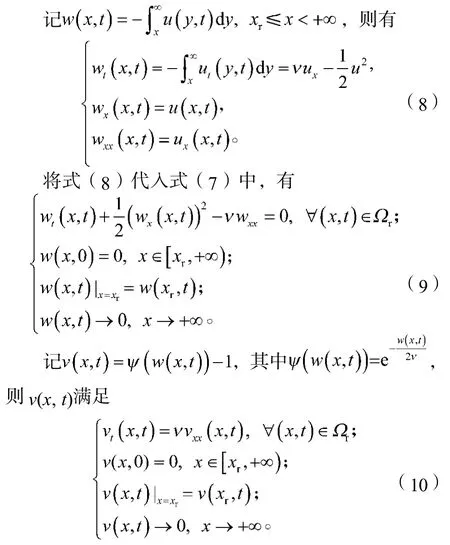
這是一個標準的熱傳導方程。

由于v(xr, t)是一個未知函數，所以問題（10）也不是一個適定問題。現在，對v(x, t)引入相對于t的拉普拉斯變換

對式（10）中第一個等式兩邊同時作拉普拉斯變換，則有

方程（11）是齊次的，有2個線性無關的特征解，分別是：

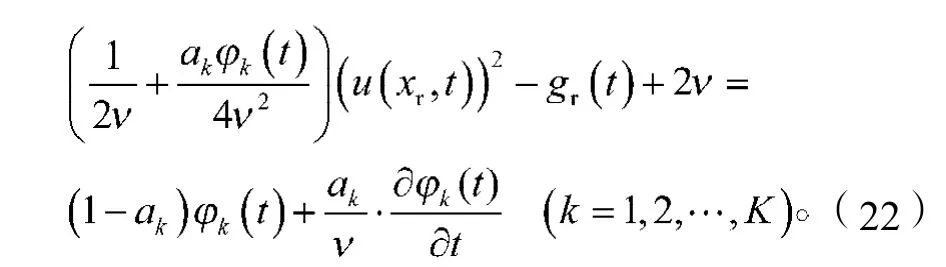
綜合式（20）與（22）可得在人工邊界x=xr上的一個局部人工邊界條件：

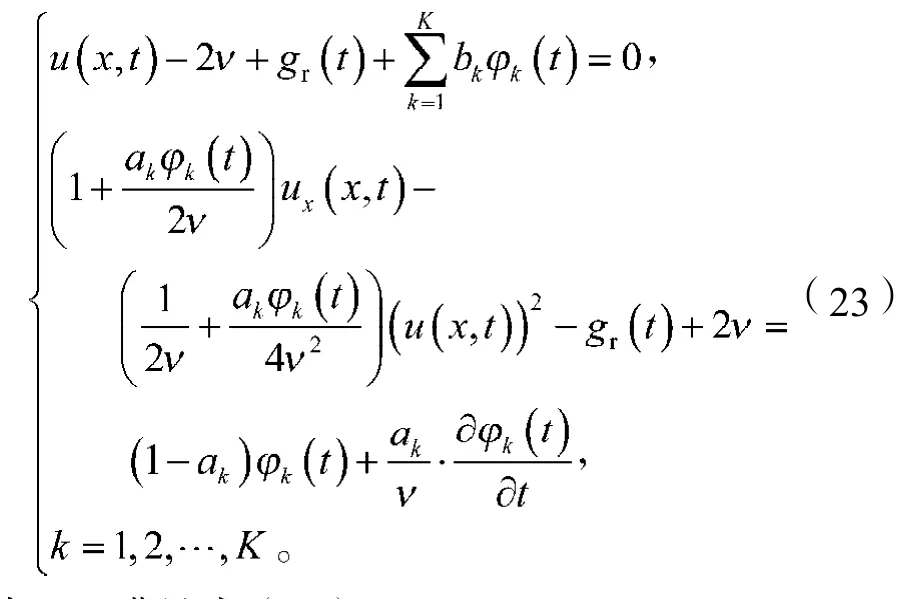
式中gr(t)滿足式（19）。

類似地，可以求得在人工邊界x=xl上的一個局部人工邊界條件為

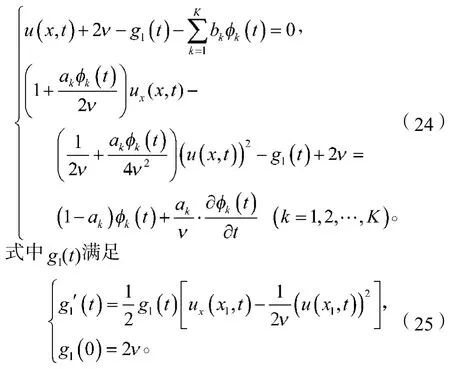
通過使用局部人工邊界條件式（23）和式（24），無界區域問題（1）可以轉化為定義在有界區域i上的初邊值問題：

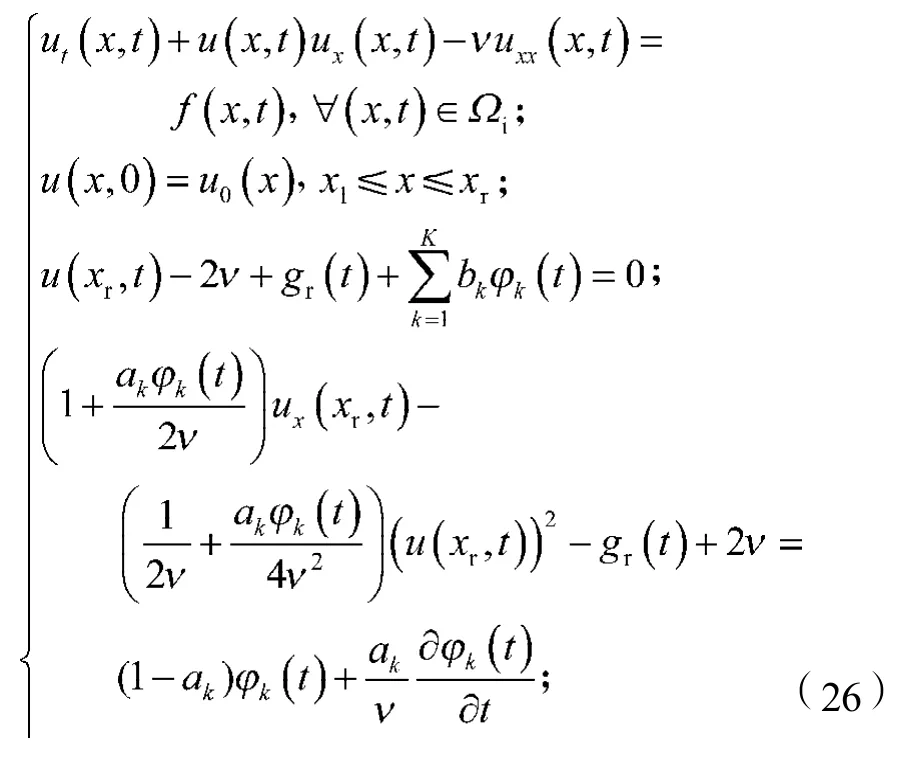
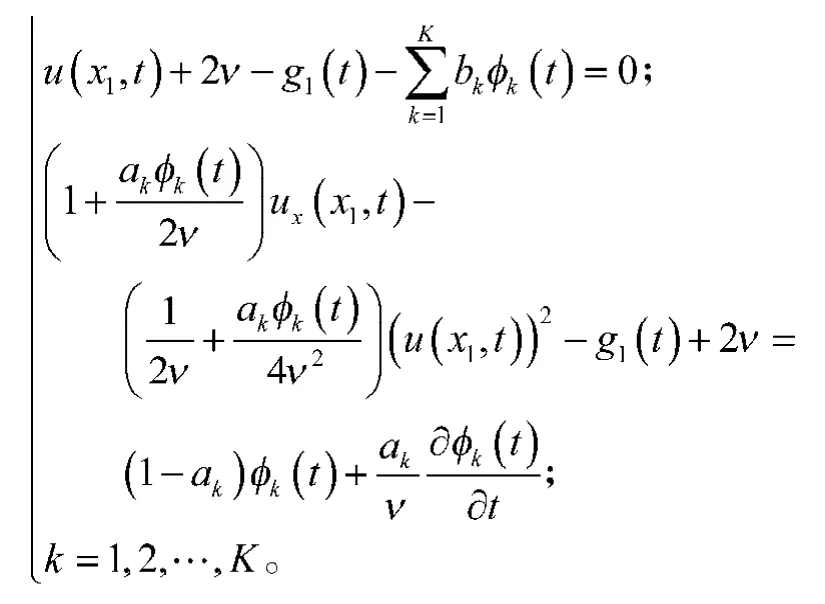
式中gt(t)和g1(t)分別滿足式（19）和（25）。這是一個非線性初邊值問題。

3 全離散差分格式的構造

首先構造非線性初邊值問題（26）的全離散差分格式。

取2個正整數M和N，并記

從而可得

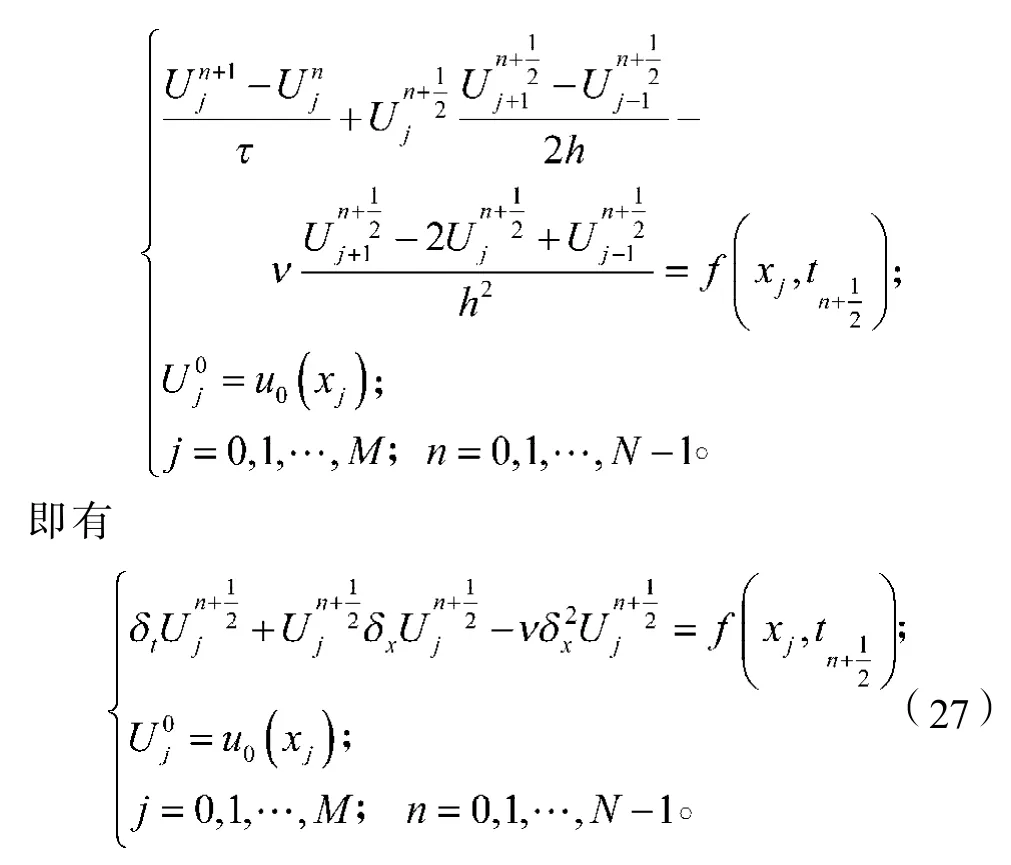
這就是二階Crank-Nicolson格式。

再考慮式（26）中邊界上的人工邊界條件的離散。

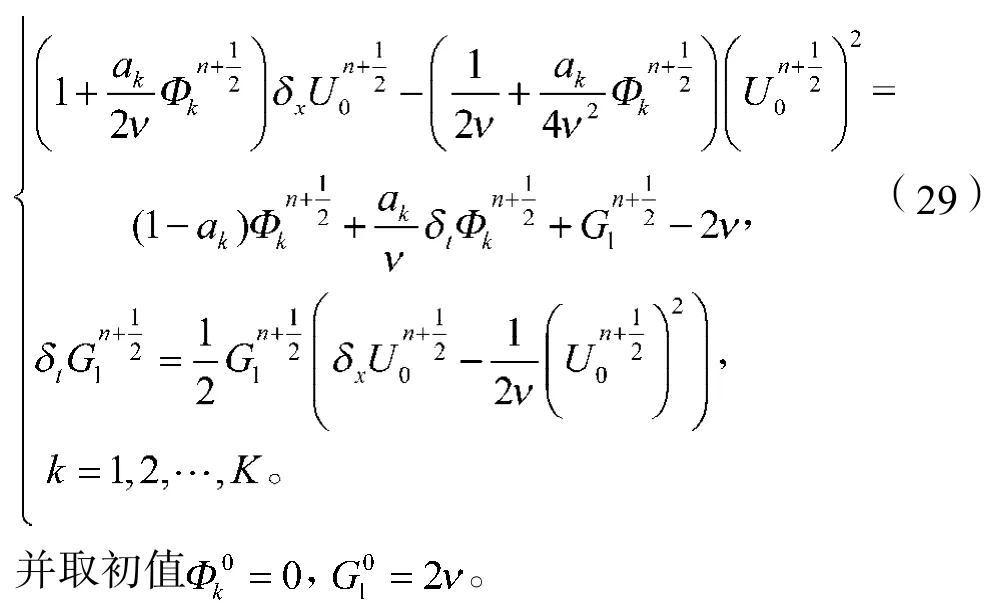
以上格式是非線性的隱式格式，可采用簡單的迭代法來求解。

4 數值實驗

考慮沒有源項的Burgers方程[7]

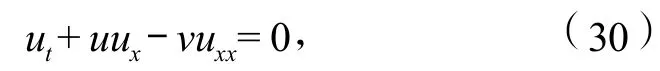
它有準確解

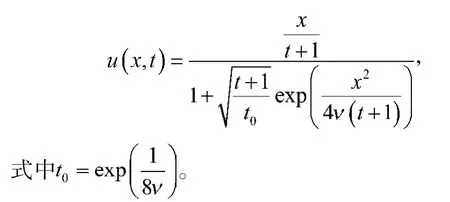
這個解表示2個波分別向左右傳播，同時波幅慢慢衰減。將它的初始值作為數值計算的初值，取=h，K=10，并計算2種不同參數的解。

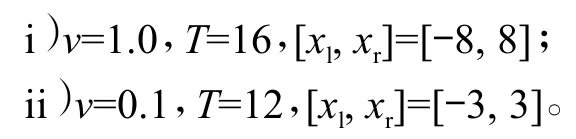
表1和表2分別列出了2種情形下誤差和精度的實驗結果，并且與文獻[7]中的數值結果進行比較，其中E∞和E1誤差分別定義為：

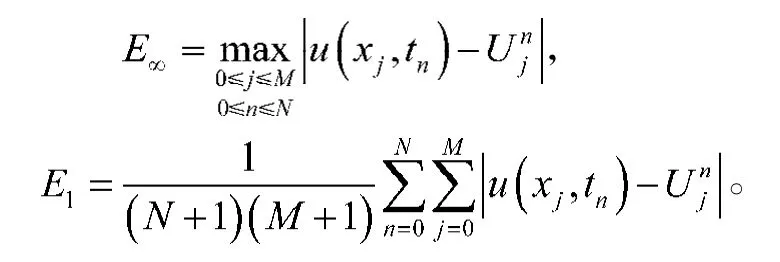
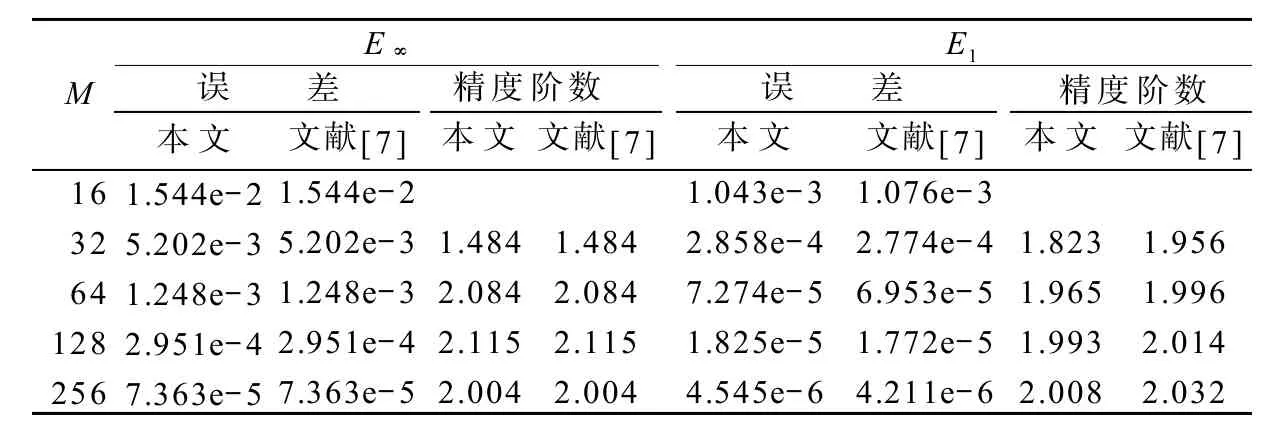
表1 當v=1.0，T=16時，E∞和E1的誤差和精度Table1The errors and accuracy for E∞and E1when v=1.0 and T=16

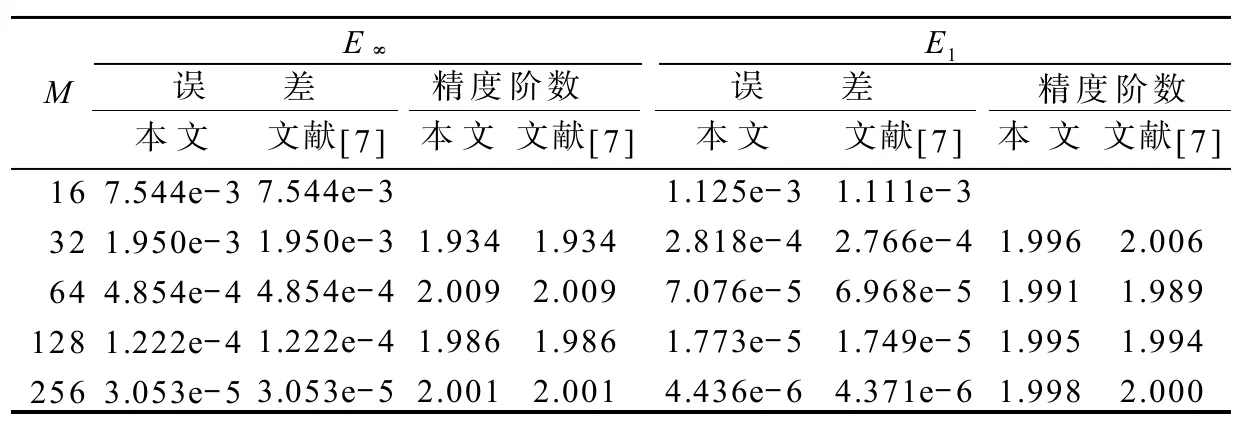
表2 v=0.1，T=12時，E∞和E1的誤差和精度Table2The errors and accuracy for E∞and E1when v=0.1 and T=12

從表1和表2中數據可知，E∞和E1都有近似2階精度。考慮到Crank-Nicolson格式的截斷誤差為，所以得到的數值解基本上達到了最佳誤差階。將本文的結果與文獻[7]中的準確人工邊界條件求出的結果作比較，可以看出2個結果相似度非常高，也說明了方法的有效性。

圖1，圖2分別是v=1.0，T=16時和v=0.1，T=12時，M取不同的值得到的相對誤差圖，其中K都取10。由圖可知，隨M的增大，數值結果逐漸逼近真解。

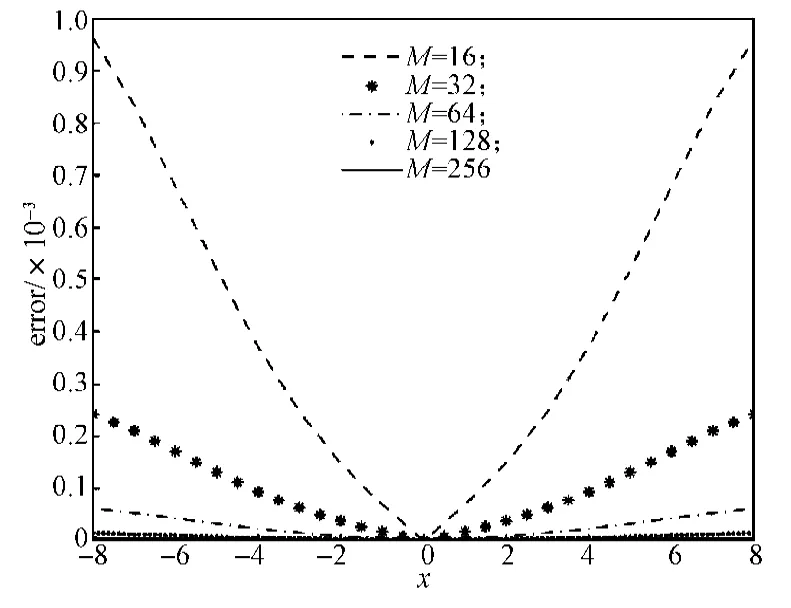
圖1 v=1.0，T=16時的相對誤差（K=10）Fig.1The relative errors (K=10) when v=1.0 and T=16

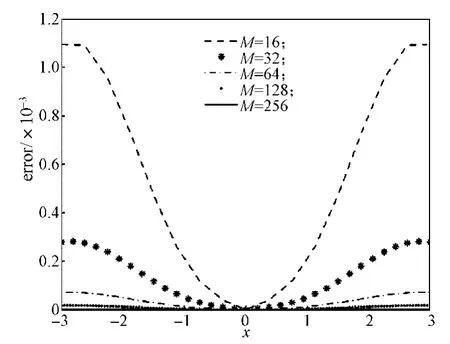
圖2 v=0.1，T=12時的相對誤差（K=10）Fig.2The relative errors (K=10) when v=0.1 and T=12

圖3和圖4是v=1.0，T=16時和v=0.1，T=12時，在Pad逼近中取不同的K值，邊界上相對誤差的變化圖，其中M=64。由圖可知，隨著K的增大，所求的邊界誤差逐漸減小，這證明了方法的有效性。

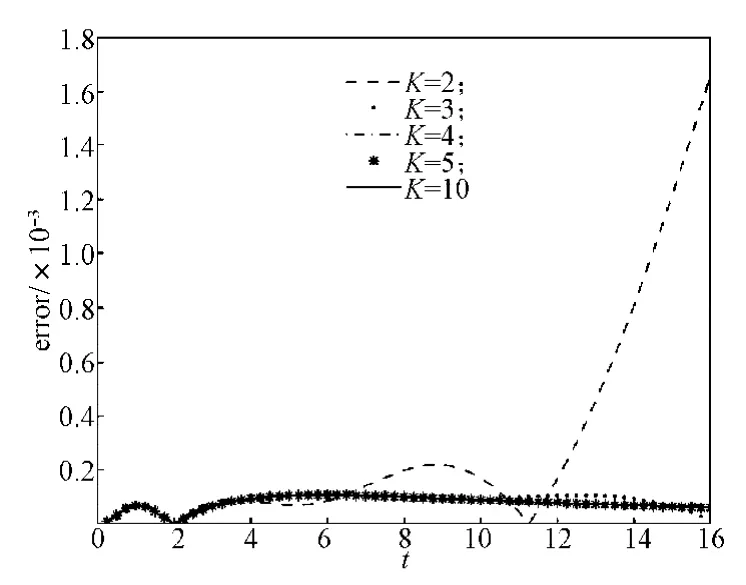
圖3 v=1.0，T=16，M=64時，邊界x=xr上的誤差隨K變化情況Fig.3The errors at buondary x=xrvarying with K when v=0.1，T=16 and M=64

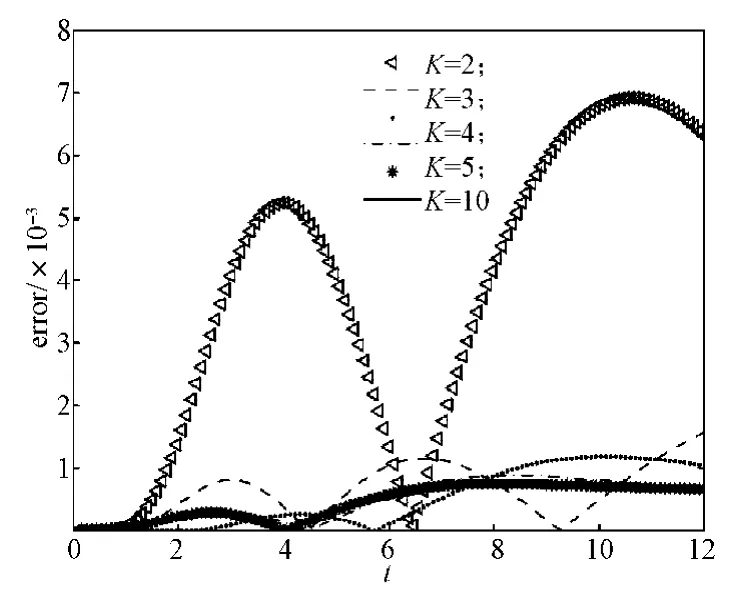
圖4 v=0.1，T=12，M=64時，邊界上的誤差隨K變化情況Fig.4The errors at buondary varying with K when v=0.1，T=12 and M=64

5 結語

針對無界域上的一維Burgers方程，本文首先運用Cole-Hopf函數變換，將非線性的Burgers方程變成線性的熱傳導方程，再運用Pad逼近得到局部的人工邊界條件。這樣的人工邊界條件與非局部的人工邊界條件相比，計算復雜性較低，存儲空間較少。數值試驗表明，本文提出的人工邊界條件，在保證計算效果的同時提高了計算的效率，因此方法是恰當和有效的。

[1]Burgers J M. A Mathematical Model Illustrating the Theory of Turbulence[J]. Advances Applied Mechanics，1949，1 (2)：171-175.

[2]Han H D，Wu X N. Approximation of Infinite Boundary Condition and Its Application to Finite Element Methods [J]. Journal of Computational Mathematics，1985，3(2)：179-192.

[3]Givoli D. Numerical Methods for Problems in Infinite Domains[M]. Amsterdam：Elsevier，1992：39-81.

[4]Goldstein C I. A Finite Element Method for Solving Helmholtz Type Equations in Waveguides and Other Unbounded Domains[J]. Mathematics of Computation，1982，39(160)：309-324.

[5]Wu X，Sun Z Z. Convergence of Difference Scheme for Heat Equation in Unbounded Domains Using Artificial Boundary Conditions[J]. Applied Numerical Mathematics，2004，50(2)：261-277.

[6]Jin J，Wu X. Analysis of Finite Element Method for One-Dimensional Time-Dependent Schrdinger Equation on Unbounded Domain[J]. Journal of Computational and Applied Mathematics，2008，220(1)：240-256.

[7]Han H D，Wu X N，Xu Z L. Artificial Boundary Method for Burgers’Equation Using Nonlinear Boundary Conditions [J]. Journal of Computational Mathematics，2006，24(3)：295-304.

[8]Wu X，Zhang J. Artificial Boundary Method for Two-Dimensional Burgers’Equation[J]. Computers & Mathematics with Applications，2008，56(1)：242-256.

[9]Sun Z Z，Wu X N. A Difference Scheme for Burgers Equation in an Unbounded Domain[J]. Applied Mathematics and Computation，2009，209(2)：285-304.

[10]Bamberger A，Engquist B，Halpern L，et al. Higher Order Paraxial Wave Equation Approximations in Heterogeneous Media[J]. SIAM Journal on Applied Mathematics，1988，48(1)：129-154.

（責任編輯：鄧光輝）

Local Artificial Boundary Conditions for One-Dimensional Burgers Equation in Unbounded Domain

Zhou Dao，Jin Jicheng
（School of Science，Hunan University of Technology，Zhuzhou Hunan 412007，China）

With respect to one-dimensional Burgers equation in unbounded domain, the nonlinear Burgers equation is firstly transformed into a linear heat equation by the Cole-Hopf function transformation, and then the artificial boundary conditions are obtained through Padé approximation, finally a finite difference discretization is applied for the obtained initial-boundary value problem. The numerical experiment shows that the proposed artificial boundary conditions are appropriate and effective.

Burgers equation；artificial boundary condition；finite difference method；Pad approximation

O241.82

A

1673-9833(2014)06-0007-06

10.3969/j.issn.1673-9833.2014.06.002

2014-09-26

國家自然科學基金資助項目（11101136），湖南省自然科學基金資助項目（14JJ2114），湖南省教育廳科學研究基金資助項目（14A164），湖南工業大學自然科學研究基金資助項目（2012HZX15）

周道（1982-），男，湖南株洲人，湖南工業大學講師，中南大學博士生，主要研究方向為偏微分方程數值解，E-mail：zhoudao_de@163.com