基于CFD的管匯非慣性水動力系數計算

湯 珂，段夢蘭，張新虎，楊 磊，郭 磊

（中國石油大學（北京）海洋油氣研究中心，北京102249） ①

隨著海洋石油開發熱點轉向深水及水下生產系統的廣泛應用，大型設備的下放安裝技術變得很關鍵。在海上安裝作業過程中，安裝船、纜和管匯整個作業系統受到海上風、浪、流的聯合作用，作業工況惡劣時風險很大。海流的水動力影響管匯安裝的順利進行，而且影響安裝作業船－纜－體的耦合運動分析［1－2］，因此研究海流對管匯的水動力作用、確定管匯的水動力系數很有必要。目前獲得水動力系數的方法主要有模型試驗、理論近似估計、流體力學（CFD）計算3種。模型試驗結果最可靠，但是模型試驗費用高、周期長。理論近似估計不可避免帶來較大的誤差。隨著CFD技術的發展，計算流體力學軟件為水動力系數的計算提供了新的有效方法，具有較高的精度且成本低，很適合于管匯水動力系數的工程計算［3］。

管匯下放入水之后，管匯受到的水動力包括附加質量力（Added Mass）和非慣性水動力（Drag and Damping Force，或稱為粘性類水動力）。工程上一般通過模型的自由運動衰減試驗和受迫振動試驗獲得。本文利用計算流體力學軟件FLUENT，對管匯周圍流場的模擬構建，給出了管匯受力情況的數值模擬，完成了計算機上的模型試驗，得到了管匯在穩態流中的非慣性水動力系數。

1 建立模型

1.1 幾何模型

圖1是針對南海1 500 m荔灣3－1氣田設計的管匯模型，其結構復雜，為便于建模和計算，需要將管匯模型進行簡化（如圖2）。為了使水動力特性相似，要求管匯各個方向的外形相似。簡化模型與原模型的比例為 1∶1，長、寬、高分別為13.5、5.2、4.5 m。

圖1 管匯模型

圖2 管匯簡化模型

在FLUENT前處理軟件ICEM中建立如圖3所示的流體域模型，尺寸為80 m×50 m×50 m，然后進行網格劃分，得到109萬個三角形非結構網格，如圖4所示。

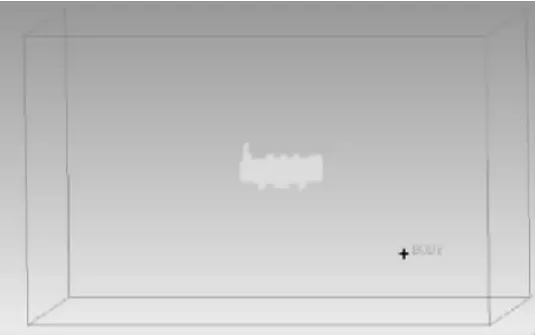
圖3 流體域模型

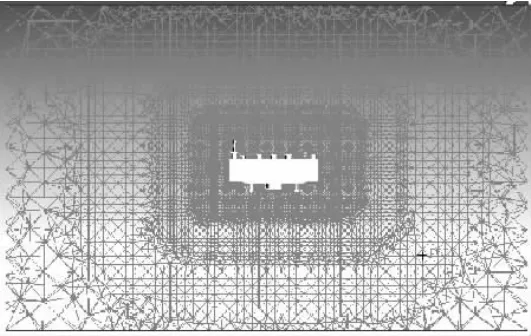
圖4 模型網格

1.2 控制方程［4－5］

求解黏性流動問題就是要解NS方程。在實際計算中，多采用雷諾時均NS方程（RANS）對引入的湍流模型后構成的封閉方程組求解得到湍流要素的時均值，求解輸出速度分量和壓力。

湍流模型主要有渦黏模型和雷諾應力模型2大類：渦黏模型中，主要有零方程和k－ε、k－ω二方程湍流模型及二方程的變形；雷諾應力模型考慮了湍流的各向異性，通常能夠給出更好的計算結果，但其數值穩定性遠不如二方程模型。工程中多采用二方程模式，本文也采用k－ε湍流模型［6］。

k方程為

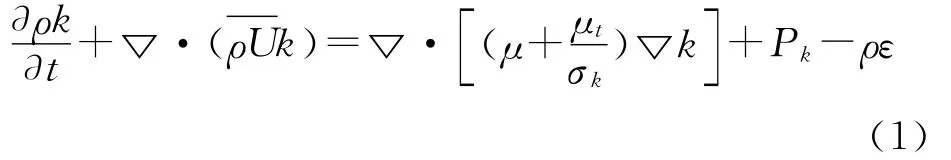
ε方程為

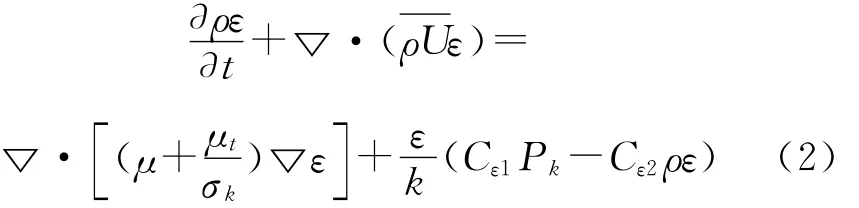
其中，

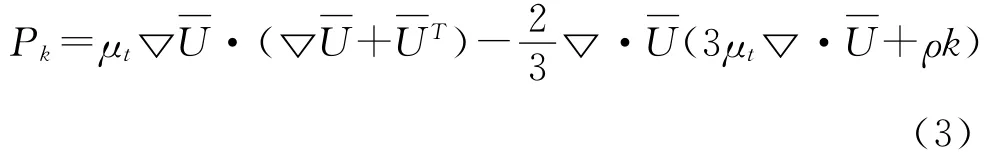
式中：μt為渦黏度為脈動動能；ε為能量耗散率。

在標準k－ε模型中，根據眾多試驗數據和廣泛湍流擬合結果，取模型常數Cμ＝0.09；σk＝1.0；σε＝1.3；C1ε＝1.44；C2ε＝1.92。

1.3 邊界條件

1） 入口處 速度入口（velocity inlet）給定速度大小、方向和湍流強度等參數。

2） 出口處 自由出流邊界（outflow）。

3） 固壁（管匯表面） 無滑移的壁面（wall）。

4） 流體域的流體性質 FLUID。

2 數值計算及結果分析

本文選擇的求解器為具有定常選項的分離一階隱式求解器，湍流模型為標準k－ε模型和標準壁面函數。流域材料定義為海水（密度為1 025 kg/m3，運動黏度為1.609×10－9m2/s）。采用SIMPLE算法求解速度與壓力耦合場，對流項中動量和壓力方程分別使用一階迎風差分離散格式。先后在縱向、橫向和垂向設置來流，求解這3個方向的管匯非慣性水動力系數（CD）。

2.1 管匯非慣性水動力系數

對于固定的管匯在外部來流作用下，由莫里森方程中非慣性水動力公式為［5］

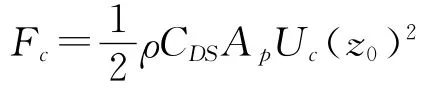
式中：ρ為流體（海水）密度；CDS為穩態海流作用下的非慣性水動力系數；Ap為海流流向的結構物投影面積；Uc（z0）為水深z0處的海流速度。

計算固定管匯的外部來流的速度為0.1、0.2、…、1.0 m/s時的管匯受力，如圖5。應用最小二乘法進行擬合并進行無因次化處理，得到管匯3個方向來流的非慣性水動力系數分別為CDSx＝0.81、CDSy＝1.00、DDSz＝1.40。

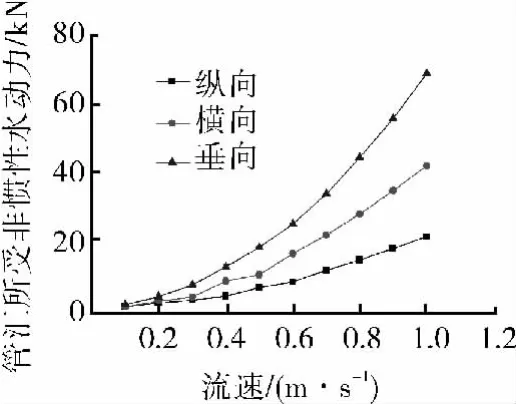
圖5 不同流速和流向的管匯受力

由于缺乏試驗數據的比較，不能較準確地確定計算誤差；但是根據DNV的相關經驗數據可以判斷計算結果至少是合理的；結構的迎流方向面積大并且扁平則水動力系數就要大一些，管匯縱向、橫向、垂向的迎流面積依次變大并且扁平，相應的水動力系數也是逐漸變大的，大小也在合理范圍內。另外，管匯周圍流場及表面壓力分布也是合理的，如圖6。

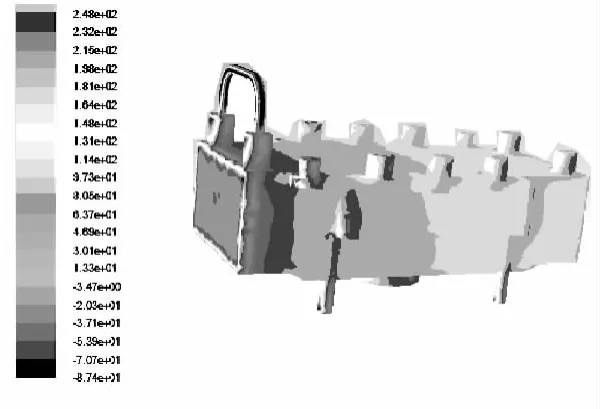
圖6 縱向來流管匯壓力分布

在管匯下放過程中，管匯受到的非慣性水動力大小取決于管匯與流體之間的相對速度［5］，即式中：CD為非慣性水動力系數；v為流體的速度；η為管匯的運動速度。

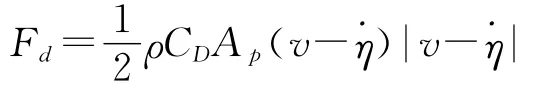
管匯隨船做振蕩運動，相當于管匯受振蕩流的作用，這時的非慣性水動力系數還跟振動周期和幅值有關，其大小大于穩態流中系數的2～3倍（約4～8）。管匯在波浪區時采用該值。在管匯下放到波浪區（wave zone）以下時，如果下放速度大于最大振動速度，那么CD的值可約取為CDS。

2.2 孔隙度對管匯非慣性水動力系數的影響

管匯在穩態流中的非慣性水動力系數的主要影響因素有：管匯的幾何外形、雷諾數、長寬比、來流方向、表面粗糙度、孔隙度。對于一個結構確定的管匯，用CFD方法求管匯的水動力系數時，要對管匯模型進行簡化。管匯孔隙度變小會影響管匯水動力系數的準確性，改變孔隙度其實也就改變了模型的幾何外形，應該重新進行計算。但對于較小孔隙度時水動力系數變化不大，當孔隙度大于15%時會有一定幅度的下降。圖7是不同孔隙度方形板的水動力系數試驗值和不同CFD模型的計算值，作為參考還需要針對管匯進行模型試驗，驗證孔隙度對水動力系數的影響［7］。

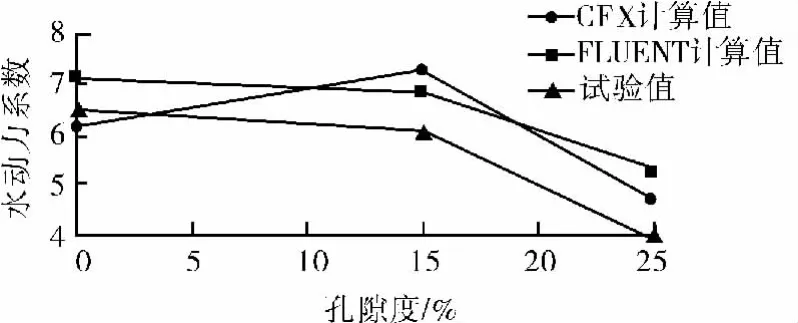
圖7 不同孔隙度方形板的水動力系數

3 結語

本文通過流體力學軟件FLUENT建立了管匯和外流場計算模型，模擬管匯在穩態流場中的水池試驗，得到了穩流場的管匯非慣性水動力系數，并分析管匯水動力系數的影響因素以及下放過程不同狀態下的水動力系數的取值方法，為使用CFD方法準確計算管匯的水動力系數打下了基礎。建議與實物模型試驗的數據進行比較，進一步優化計算模型和參數，使CFD計算水動力系數成為成熟技術，對避免模型試驗的長周期和高成本具有重要的意義。

［1］ Roveri F E，Oliveira M C，Moretti M J.Installation of a Production Manifold in 2000 ft Water Depth Offshore Brazi ［G］.Offsh ore Technology Conference，OTC8237，1996：763－773.

［2］ 姚麗琳.深水水下安裝下放運動分析技術研究［D］.上海：上海交通大學，2011.

［3］ 張赫，龐永杰，李曄.基于FLUENT軟件模擬平面運動機構試驗［J］.系統仿真學報，2010，22（3）：566－569.

［4］ 萬富濱，袁力，胡知輝.基于CFD數值模擬的立式中心攪拌器有限元分析［J］.石油礦場機械，2008，37（8）：52－55.

［5］ 許超，付建紅，趙志強，等.基于CFD軟件的渦輪流動特性數值模擬及敏感性分析［J］.石油礦場機械，2012，41（4）：16－20.

［6］ 胡志強，林揚，谷海濤.水下機器人粘性類水動力數值計算方法研究［J］.機器人，2007，29（3）：145－150.

［7］ DNV－RP－H103.Modelling and Analysis of Marine Operations［S］.DNV，2011.