洞室群圍巖應力集中效應放大現象的數值模擬

陳永前 邢博瑞，2 李 鳳

（1.中國地震局地殼應力研究所 地殼動力學實驗室，北京 100085；2.中國地質大學，北京 100083；3.河北省地震局，石家莊 050021）

從20世紀末開始持續至今，隨著水利水電工程建設的不斷增多，洞室群施工及穩定性控制問題成為地下工程研究領域的熱點［1-3］.國內外專家學者主要通過數值模擬來研究洞室群的應力場、位移場的分布規律和洞室群的穩定性問題.國內學者王成虎［4-5］結合新疆某水電站的深部洞室群穩定性研究工作，利用三維數值模擬軟件3D－Sigma模擬洞室群圍巖應力場變化，發現了“洞室群應力集中效應放大現象”，即后期的洞室施工對鄰近洞室的應力場有惡化效應，加劇了前期開挖洞室的應力集中.朱維申等［6］通過數值模擬方法計算了上百個算例，研究了4大巖類、4種埋深在不同側向地應力條件下洞壁位移量的變化規律，并擬合出用多項式表達的公式，以預測圍巖在不同條件下的位移量.劉朝幀、周德培、洪開榮等［7-8］通過對太平驛水電站引水隧道的巖爆災害統計分析，發現在太平驛引水隧道中，巖爆一般發生在隧道斷面內兩個固定的地點，且巖爆發生高峰期均在開挖后一個特定的時間段內.

自20世紀80年代以來，國外許多學者通過大型地下深埋試驗場對深埋隧洞的圍巖應力分布進行研究.Tasaka和Kaiser根據隧洞開挖后圍巖應力分布的主應力大小，提出了地下洞室開挖完成后脆性巖體裂紋起裂和裂紋破壞的應力門檻值，利用這個理論可以判斷圍巖損傷區的大小［9-10］；Backblom認為圍巖破壞區的形成主要是圍巖應力重分布導致鄰近開挖面巖體的整體或局部屈服及其往外發展所引起的［11］，以及洞室圍巖中拉應力區的存在也是圍巖出現破壞區的主要原因之一［12］.

通過上述分析發現，前人對洞室群的研究主要集中在穩定性評價和穩定性控制這兩個方面，對洞室群在開挖過程中應力場之間的相互影響規律研究甚少.鑒于此，本文利用數值模擬軟件3D－Sigma設計了4組模型，試圖發現一些洞室開挖過程中應力場應力集中效應放大的規律［13-15］.

1 數值模型的構建

1.1 模型設計

本文旨在通過數值模擬（3D－Sigma）來分析洞室群在開挖過程中后期洞室的開挖對前期洞室圍巖應力場的影響，以及隨著兩洞室的相對距離變化圍巖應力場的變化規律［16］.模型分別考慮洞室間距、洞室截面形狀、洞室水平軸線的相對位置等參數的變化.對于模型的截面形狀，主要考慮直墻半圓拱和圓形截面兩種典型地下空間截面形狀.為分析洞室截面圍巖中的應力變化，首先在開挖的洞室截面典型應力集中部位設置應力監測點.在分步開挖過程中，依次記錄監測點的應力狀態，然后分析其變化規律，再現鄰近洞室開挖對現有洞室影響的應力集中放大效應.本文建立4組模型來研究圍巖洞室的應力集中放大效應（如圖1所示）.

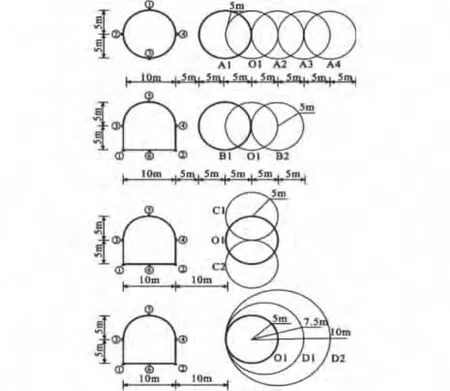
圖1 數值模擬模型及應力監測點布置示意圖

第1組模型包含兩個圓形洞室，洞室半徑r為5 m.以洞室半徑為單位逐級增加建立5個模型.其中，L表示每個模型中兩洞室之間的距離（系指兩洞室間巖壁厚度），洞距分別為1r＝5m（A1模型）、2r＝10m（O1模型）、3r＝15m（A2模型）、4r＝20m（A3模型）、5r＝25m（A4模型）.

第2組模型包含直墻半圓拱形和圓形洞室，其中直墻半圓拱洞室拱半徑為5m、直墻為5m，圓形洞室半徑r為5m.兩洞室大小不變，以洞室半徑為單位逐級增加洞間距建立3個模型，洞距分別為1r＝5m（B1模型）、2r＝10m（O1模型）、3r＝15m（B2模型）.

第3組模型包含兩個洞室，其中直墻半圓拱洞室半徑為5m、直墻為5m，圓形洞室半徑r為5m.兩洞室大小不變，以洞室半徑為單位變化圓形洞室的相對豎直深度建立3個模型，模型洞距L為2r＝10m.

第4組模型洞室間距（兩洞室間巖壁厚度）和直墻拱洞室不變，以圓形洞室半徑變化建立3個模型，兩洞室間巖壁厚度為10m，每個模型圓形洞室的半徑r分別為r＝5m（O1模型）、r＝7.5m（D1模型）、r＝10m（D2模型）.

1.2 模型尺寸及邊界條件

為了更好地模擬實際情況，減少計算模型的邊界條件對隧道圍巖的影響，本文選取模型尺寸為150m×135m×60m（如圖2所示）范圍的巖體進行建模［17-18］.計算剖分單元8064個，節點36375個.根據工程巖體變形破壞特點，在模擬過程中將巖體模型設計為彈性模型.

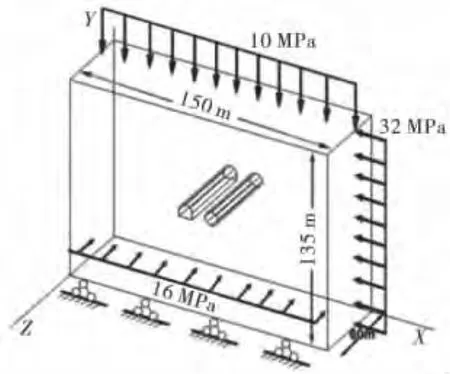
圖2 數值模型的尺寸和邊界條件

因此，采用以下邊界條件：①模型的上端面加10 MPa豎直向下的應力，在前面施加16MPa的水平應力，方向指向Z軸負方向.在右端面施加32MPa的水平應力，方向指向X軸負方向；②在模型的后、左及下端面均采用了沿相應法線方向上的零位移約束，即認為模型后、左及下端面以外的地質體為剛性體，不允許其產生法向的移動.

模型中巖體計算參數：彈性模量E＝30000 MPa；泊松比μ＝0.25；內摩擦角Ф＝45°；比重γ＝26.5kN／m3；黏聚力C＝3MPa；抗拉強度σt＝0.332 MPa.

1.3 開挖方式及監測點的布置

為了尋找洞室群開挖過程應力場變化規律，首先在模型中已開挖的圓形洞室或者直墻拱洞室上設立監測點（如圖1，在直墻拱洞室中，邊墻與底板的相交處①、②點，洞室圓拱與邊墻的相交處③、④點，拱頂⑤點和洞底面中間⑥點），然后對后期開挖的圓形洞室分步開挖.模型中隧洞的分步開挖利用軟件中的“階段”設置功能來實現，“階段”反映了一個時間的概念（圖4中的橫坐標／步），模擬共設計為13階段，其中第1階段為模型的初始化.蘇永華［19］等通過有限元法模擬大跨度地下洞室開挖順序對隧道穩定性的影響，得出先拱后墻的開挖順序對隧道圍巖的破壞性更小.故本文采用先拱后墻的開挖方式，即先開挖隧道半圓拱的部分，再開挖直墻部分.后期洞室每開挖一步，就對前期洞室的應力變化影響一點.由于在前期洞室布置了監測點，所以就可以得到后期洞室整個開挖過程中，前期洞室的應力變化值.然后再分析這些應力值的變化規律以及應力集中的放大規律.

2 洞室群開挖過程應力場變化規律

在深部洞室群開挖過程中，應力場是相互發生疊加影響的.數值模擬結果表明，無論哪組模型，整個洞室群開挖結束后，圍巖在原地應力場的作用下向臨空面方向移動，產生了不均勻的變形，也改變了應力場的空間分布特征，同時產生了一些應力集中區［20］（如圖3所示）.應力集中區主要出現在圓形洞室的拱頂、拱底和左右拱腳，而應力降低區主要位于洞室各應力集中點之間的區域.最小主應力總體分布規律與最大主應力相似.

圖3 洞室群開挖后主應力σ1的等值線（單位：MPa）

2.1 對第1組模型的應力集中放大現象

本組包含5個模型，分別為水平洞間距不同的5個模型.通過在前期開挖洞室布置監測點，測出了在后期開挖洞室的開挖過程中前期洞室的應力值，并分析應力值得出如下規律.限于篇幅，僅給出第1組模型中各個監測點的主應力變化率隨不同開挖階段分析曲線圖（如圖4所示）.

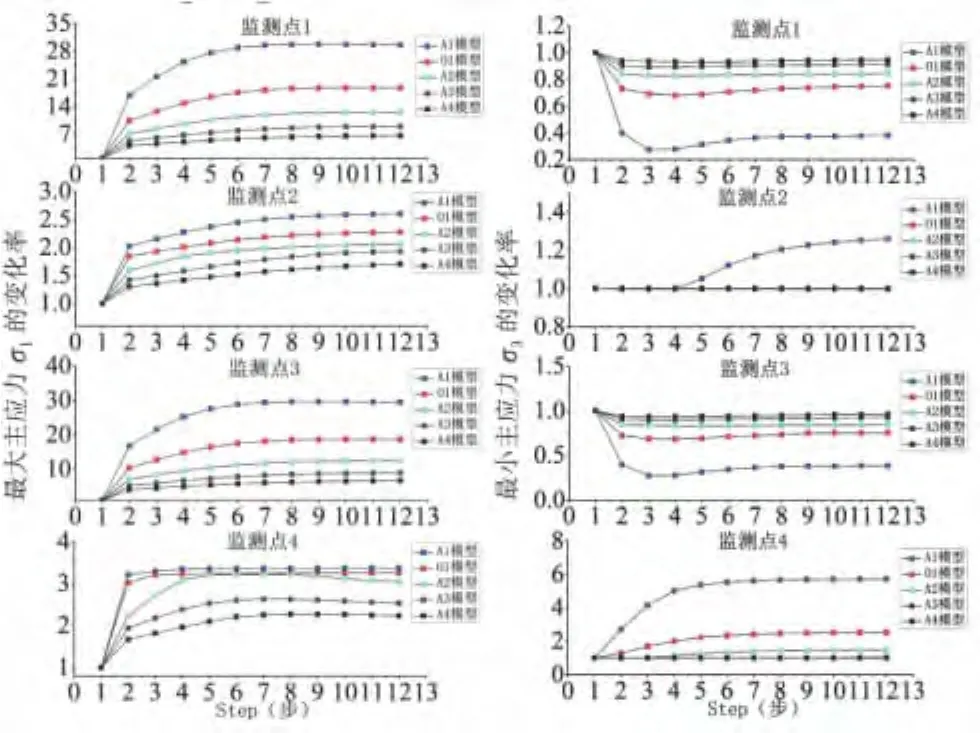
圖4 第1組主應力的變化率與開挖階段的關系曲線

應力集中放大效應：①由圖4得知，相互對稱的監測點1（拱頂）和監測點3（拱底）受后期開挖洞室影響比較明顯，即應力集中效應放大現象比較顯著，而且變化規律很相似.可見后期洞室開挖對前期洞室的拱頂和拱底影響較大.②從圖4中可以看出，洞室間距越小，前期洞室的應力集中效應放大現象越顯著.隨著洞室間距的增加，后期洞室開挖對前期洞室的影響越來越不明顯，并且隨著后期洞室開挖階段的增加，洞室間的應力場最后趨于穩定.可見空間上應力場的相互影響程度是不同的.

2.2 對第2組模型的應力集中放大現象

本組模型中包含3個模型，分別為水平洞室間距不同的3個模型，前期開挖洞室的斷面形狀為直墻拱形.各點均受洞室之間應力場的影響，但由于監測點與后期開挖的圓形洞室距離不同，所以產生的影響也不同.各個監測點的主應力變化率隨不同開挖階段分析曲線圖如圖5所示.

應力集中放大效應：①由圖5可以看出，在B1、O1和B2模型中，只有在B1模型中后期洞室的開挖對前期洞室的影響最為顯著，B2模型中對前期洞室的影響最不明顯.可見對于水平洞室間距不同的洞室來說，前期洞室離后期洞室的距離越近，后期開挖洞室對前期開挖洞室的應力場影響越顯著.②從圖5可以看出，在B1模型中監測點2和監測點4的主應力變化率比較顯著，特別是監測點2（右直墻腳）的主應力變化率最為顯著.可見應力場相互之間的影響對已有的應力集中效應有放大作用.③通過和第1組模型的對比發現，在洞室間距相同的情況下，第2組模型應力集中效應更顯著，即前期開挖洞室截面形狀為直墻拱比截面形狀為圓形的模型應力集中效應更顯著.可見水平洞室間距一定的情況下，圓形開挖洞室更穩定.④在最小主應力變化率的圖表中可以看出，除了監測點2和監測點4受洞室間的應力場影響較明顯之外，監測點5（拱頂）和監測點6（底面中點）應力值變化也非常顯著.說明在鄰近洞室開挖時，洞頂和底板中點也是最容易受到破壞的部位.⑤在后期洞室開挖過程中，前期洞室的各個監測點都受到了不同程度的影響，但隨著后期洞室的開挖，各個監測點的應力值趨于穩定，可見應力場是有一定范圍的.

2.3 對第3組模型的應力集中放大現象

本組包含3個模型，分別為后期開挖洞室在洞間距為10m處的豎直方向上變化的3個模型.各點均受洞室之間應力場的相互影響，但由于監測點與后期開挖洞室的豎直位置不同，產生的影響也不同.為了尋找這種洞室的開挖方案的應力集中效應的規律，本文分析了監測點的應力值.各個監測點的主應力變化率隨不同開挖階段分析曲線圖如圖6所示.

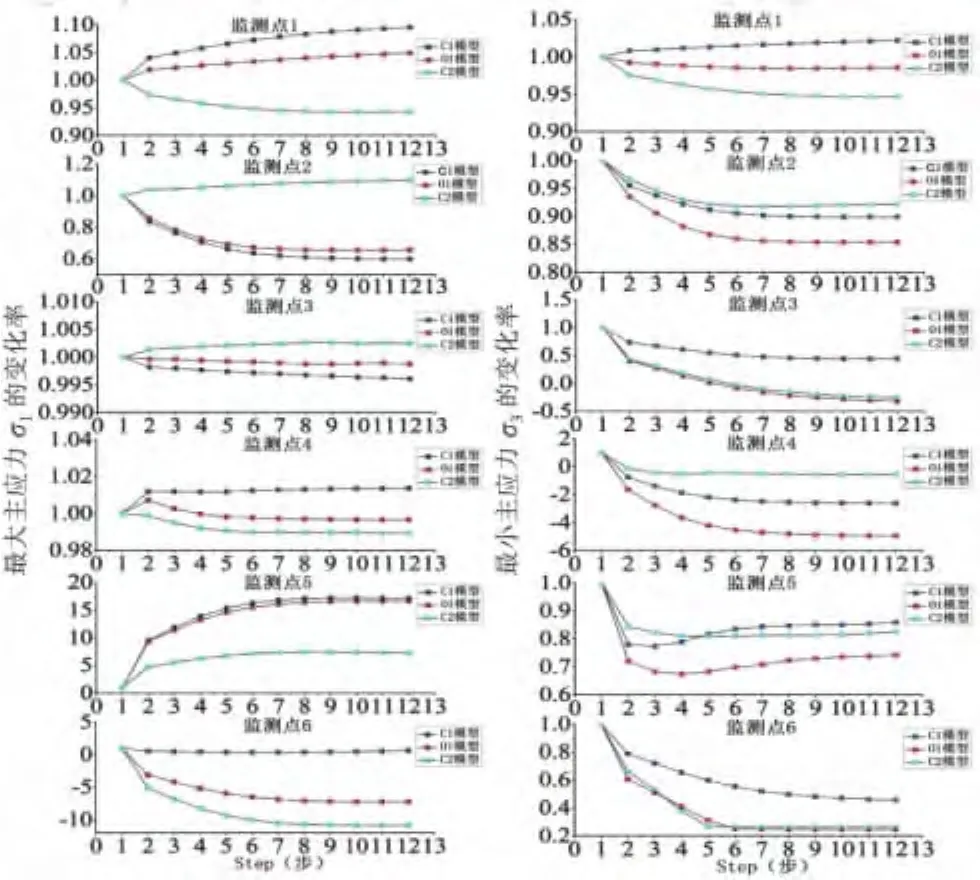
圖6 第3組主應力變化率與開挖階段的關系曲線

應力集中放大效應：①從最大主應力σ1的變化率可以看出，C1和C2模型中前期洞室的各個監測點的應力值變化較為顯著，O1模型對前期洞室的影響較小.可見后期開挖洞室與前期已開挖洞室在一個水平面上應力場的相互影響是最小的.②以監測點6（底板中點）為研究對象，在圖6中可以發現，C2模型比C1模型對監測點6的影響更大，因為監測點6離C2模型更近.同樣在圖6中可以發現，C1模型比C2模型對監測點5（拱頂）的影響更大，因為監測點5離C1模型更近.可見在水平洞間距一定的情況下，后期洞室的開挖對前期洞室的洞頂和底板中點等部位影響比較大；但如果開挖洞室在豎直方向上變化，離挖洞室近的監測點受到開挖過程應力場的影響更大.③前期洞室不同位置的監測點相互比較（監測點1和監測點3、監測點2和監測點4），可以發現在二次應力重新分布中應力變化大的監測點，受到后期洞室開挖應力場影響同樣也很顯著［21］.

2.4 對第4組模型的應力集中放大現象

本組包含3個模型，分別是后期開挖洞室與前期開挖洞室的水平間距一定，但后期開挖洞室的直徑不同的3個模型.根據前期洞室的監測點得出的應力值可以發現各個監測點均受到后期開挖洞室的應力場的影響，但由于監測點與后期開挖的圓形洞室直徑不同，產生的應力集中大小也不同.各個監測點的主應力變化率隨不同開挖階段分析曲線圖如圖7所示.

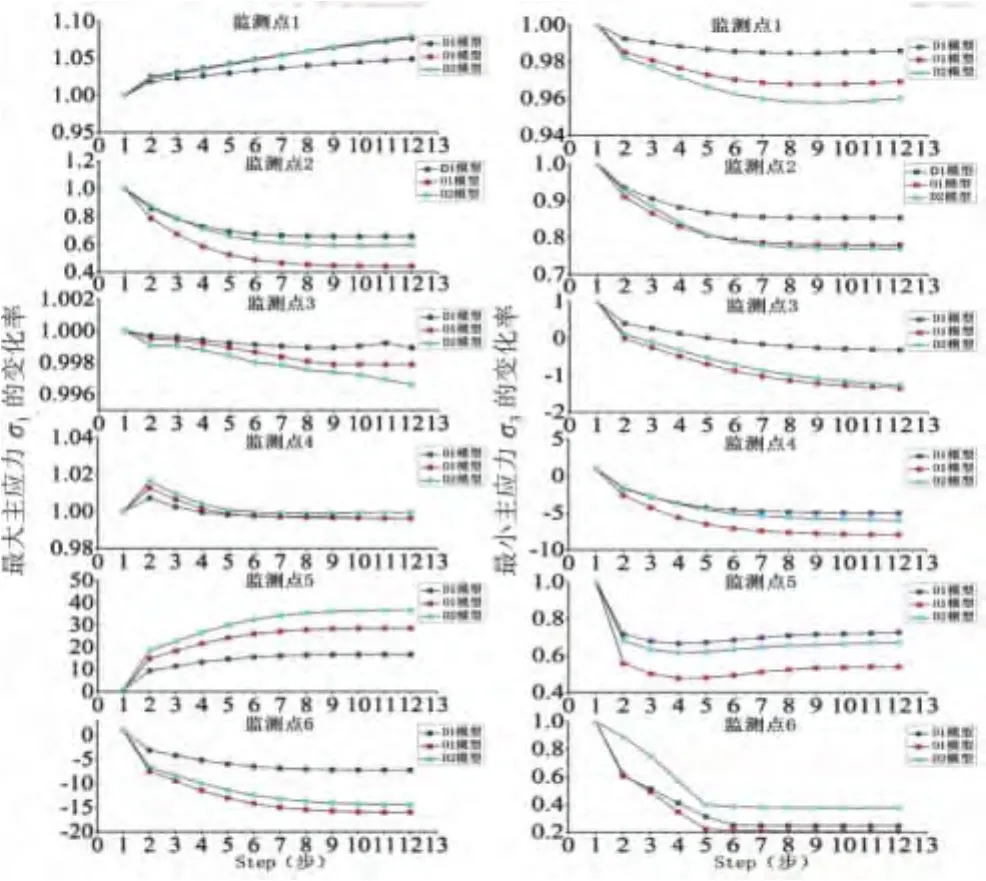
圖7 第4組主應力變化率與開挖階段的關系曲線

應力集中放大效應：①由圖7可以看出，各個模型中相互對稱的監測點（監測點1和監測點2、監測點3和監測點4），最小主應力變化率的趨勢基本一致，說明3個模型中的后期洞室的開挖對前期洞室的惡化規律基本相似，但其中距后期開挖洞室近的監測點變化較大.②通過圖7中曲線的變化趨勢可以看出，應力集中效應放大現象隨著后期洞室直徑的增大，應力集中效應更加顯著.可見在一定的洞室間距下，后期開挖洞室的直徑越大，應力集中效應放大現象越顯著，也就是說后期開挖洞室對前期開挖洞室的影響越大.③在所有受影響的監測點中，監測點5（拱頂）和監測點6（底板中點）變化最為顯著.說明前期洞室的拱頂和底板是比較薄弱的部位，容易受到后期洞室的影響.

3 數值模擬結果討論

在大規模地下洞室群開挖過程中，通過圍巖變形監測來調整和修改地下工程的開挖方案和支護參數是保證地下工程穩定的必要手段［22］.本文參考大朝山水電站［23-24］、小浪底工程廠壩區［25］、龍灘水電站［26］、二灘水電站［27］等地下洞室安全監測資料，將各水電工程地下洞室的應力數據變化規律與本文數值模擬結果進行比較討論：

1）后期洞室的開挖對前期洞室的應力集中的改變，受洞室間距的影響，即洞室間距越小，前期洞室的應力集中效應越顯著.隨著洞室間距的增加，洞室群各洞室間應力場的相互影響逐漸減小.原因在于當兩個洞室之間距離較近時，會造成波在兩個洞室之間多次反射，兩個洞室之間的相互作用比較明顯，因而在兩個洞室相對的區域會出現顯著的動應力集中.正如王虎成提出的“洞室群應力惡化效應”，即當2個洞室相距很近時，會出現“強化應力集中效應”的現象，這對整個洞室的穩定非常不利.特別是對于應力集中點很多的復雜斷面洞室群，首先開挖斷面簡單、應力集中點相對少的洞室，而后開挖斷面形狀復雜，應力集中點相對較多的洞室，這樣可以降低施工擾動對洞室群應力場的影響.潘祖弼［28］通過對石灰巖體中的隧洞圍巖進行波速測定以及對法國伊澤爾-阿爾克隧洞的應力測量得出在洞室開挖之后，應力變化影響范圍為1.5～2倍洞徑，應力集中的大小約為初始應力的2～3倍.因此可根據該規律，選擇大于應力影響范圍的洞距，這樣有利于提高洞室群的穩定性.

2）洞室二次應力重分布受洞室形狀影響，在一些特殊位置如直墻拱洞室，邊墻和底板交接點出現應力集中值很高的區域，而后期洞室的開挖對這些應力集中區域進一步惡化往往更嚴重，因此在水平洞室間距一定的情況下，圓形開挖洞室更穩定［29］，如大朝山水電站地下廠房觀測結果表明，變形和應力最大值均發生在觀測面的上、下游邊墻部位，部分測值已超過設計計算值，而且仍有蠕變現象.這與本文提出的左右直墻拱腳應力集中效應比其他部位顯著基本吻合.因此，對于地應力較高的區域開挖洞室，應盡量采用圓形和圓弧形斷面，這對降低洞室維護成本，減少安全事故都有重要的現實意義［30］.

3）后期開挖洞室與前期已開挖洞室在一個水平面上應力場的相互影響是最小的.因為若不在同一水平面時，就會引起二次應力重分布不均勻、不對稱.而當應力分布不對稱時，則洞體村砌及巖體變形亦不對稱，容易產生偏傾壓力，對洞體的支護及襯砌很不利.一般而言，最大水平主應力與洞室主軸線夾角越小則洞室群穩定性越好，夾角越大則洞室群穩定性越差.例如，黃島地下水封洞庫洞室群規模大，且采用平行布置，就是因為洞室主軸線布置對洞室群穩定性至關重要［31］.又如我國龍灘水電站、二灘水電站均采用主廠房、主變洞和尾水調壓井三大主洞室依次平行布置，從而最大程度減少支護，加強洞室群的穩定性.

4）通過模擬發現，在一定的洞室間距下，開挖洞室的洞徑越大，應力集中放大效應越顯著，即后期開挖洞室對前期開挖洞室的影響越大.韓嘯［32］以黃河地質博物館工程為研究背景，運用FLAC－3D進行數值模擬發現，隨著洞徑從5m縮小為2.5m，洞徑越小，開挖后應力收斂趨進于零的速度越快，即圍巖土體應力重分布達到穩定速度越快，這是因為土體發生變形后，變形的影響在土體中蔓延，洞徑尺寸不同，產生應力釋放時效不同所造成的.另外，洞室洞徑越小，X、Z方向位移值越小，洞室越穩定.因此，選擇合適的洞徑尺寸對于洞室群的穩定與安全有著重要的意義.

4 結 論

通過前面的對洞室群應力集中效應放大現象的數值模擬分析研究，我們得到如下結論：

1）后期洞室開挖對前期洞室應力集中的影響，受洞室間距以及洞徑的影響，洞室間距越小，開挖洞室的洞徑越大，應力集中放大效應越顯著，后期開挖洞室對前期開挖洞室的影響越大.

2）在洞室群設計中，選擇圓弧形斷面并且盡量保持洞室群平行排列，可以降低洞室群應力的變化，增加洞室穩定性.

3）本文研究的結果與實際工程監測結果基本一致，但是只考慮到完整巖體的洞室開挖的情況，沒有考慮裂隙和軟弱結構面的影響，還需進一步的深入研究.

［1］王后裕，陳上明，言志信，等.地下洞室斷面和間距優化計算的分布密度法［J］.工程力學，2004，21（3）：204－208.

［2］崔思嚴.地下廠房洞室群巖柱厚度、洞跨與洞高的統計相關分析［J］.四川水力發電，2006，25（5）：81－84.

［3］王成虎，郭啟良，侯硯和，等.地下水封油庫場址原地應力場及工程穩定性分析研究［J］.巖土工程學報，2010，32（5）：698－705.

［4］王成虎，何滿潮.水電站深部洞室群應力場相關性研究［J］.湖南科技大學學報：自然科學版，2007，22（1）：56－60.

［5］王成虎，何滿潮.水電站深部洞室群應力惡化效應初探［J］.礦冶工程，2006，26（6）：28－31.

［6］朱維申，李曉靜，郭彥雙，等.地下大型洞室群穩定性的系統性研究［J］.巖石力學與工程學報，2004，23（10）：1689－1693.

［7］劉朝禎.太平驛引水隧洞巖爆的預測和防治［J］.鐵道建筑技術，1994（3）：8－12.

［8］周德培，洪開榮.太平驛隧洞巖爆特征及防治措施［J］.巖石力學與工程學報，1995，19（2）：171－178.

［9］Cai M，Tasaka P K，Maejima Y.Generalized Crack Initiation and Crack Damage Stressthresholds of Brittle Rock Masses Near Underground Excavations［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41（5）：833－847.

［10］Cai M，Kaiser P K，Martin C D.Quantification of Rock Mass Damage in Underground Excavations from Micro Seismic Event Monitoring［J］.International Journal of RockMechanics and Mining Sciences，2001，38（7）：1135－1145.

［11］Backblom G，Martin C D.Recent Experiments in Hard Rocks to Study the Excavationresponse：Implications for the Performance of a Nuclear Waste Geological Repository［J］.Tunneling and Underground Space Technology，1999，14（3）：377－394.

［12］Read R S.20Years of Excavation Response Studies at AECL's Underground Research Laboratory［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41（8）：1251－1275.

［13］安紅剛，馮夏庭.大型洞室群穩定性與優化的進化有限元方法研究［J］.巖土力學，2001，22（4）：373－377.

［14］安紅剛，馮夏庭，李邵軍.大型洞室群穩定性與優化的并行進化神經網絡有限元方法研究-第一部分：理論模型［J］.巖石力學與工程學報，2003，22（5）：706－710.

［15］安紅剛，馮夏庭.大型洞室群穩定性與優化的并行進化神經網絡有限元方法研究-第二部分：實例研究［J］.巖石力學與工程學報，2003，22（10）：1640－1645.

［16］朱維申，孫愛花，王文濤，等.大型洞室群高邊墻位移預測和圍巖穩定性判別方法［J］.巖石力學與工程學報，2007，26（9）：1729－1736.

［17］王成虎，丁立豐，李方全，等.川西北跨度23年的原地應力實測數據特征及其地殼動力學意義分析［J］.巖石力學與工程學報，2012，31（11）：2171－2181.

［18］王成虎，張彥山，郭啟良，等.工程區地應力場的綜合分析法研究［J］.巖土工程學報，2011，33（10）：1562－1568.

［19］蘇永華，方祖烈，高 謙.大跨度地下洞室開挖的模擬分析［J］.礦業研究與開發，1998，18（4）：1－3.

［20］王成虎，沙 鵬，胡元芳，等.隧道圍巖擠壓變形問題探究［J］.巖土力學，2011，32（S2）：143－147.

［21］王成虎，郭啟良，賈 龍.基于Hoek－Brown強度準則的高應力判據理論分析［J］.巖土力學，2011，32（11）：3325－3332.

［22］張志國，肖 明.地下洞室監測位移場的反演和圍巖穩定評判分析［J］.巖石力學與工程，2009，28（4）：813－818.

［23］郭心銳，周正新.大朝山水電站地下洞室安全監測淺析［J］.云南水力發電，2003，19（2）：75－78.

［24］郭 晨，劉愛梅，管 輝，等.大朝山水電站地下洞室安全監測資料分析［J］.水力發電，2005，31（12）：89－91.

［25］孫民偉，杜建中.小浪底工程地應力測試及其特征分析［J］.長江科學學院院報，1996，13（增刊）：20－23.

［26］張孝松.龍灘水電站地下洞室群布置及監控設計［J］.巖石力學與工程學報，2005，24（21）：3893－3989.

［27］季良杰，李文慧.二灘水電站地下廠房洞室群圍巖變形機理研究［J］.水電工程研究，2000（4）：68－80.

［28］潘祖弼.隧洞群中的應力干擾［J］.華東水電技術，1992（1）：17－22.

［29］王成虎，郭啟良，丁立豐，等.工程區高地應力判據研究及實例分析［J］.巖土力學，2009，30（8）：2359－2364.

［30］王成虎，宋成科，劉立鵬.地下空間圍巖脆性破壞時的應力特征研究［J］.巖土力學，2012，33（S1）：1－7.

［31］張玉升.黃島地下水封洞庫洞室群合理主軸線方位探討［J］.勘察科學技術，2011（4）：43－45.

［32］韓 嘯.土體洞室開挖的力學參數敏感性分析［D］.鄭州：華北水利水電大學，2013.