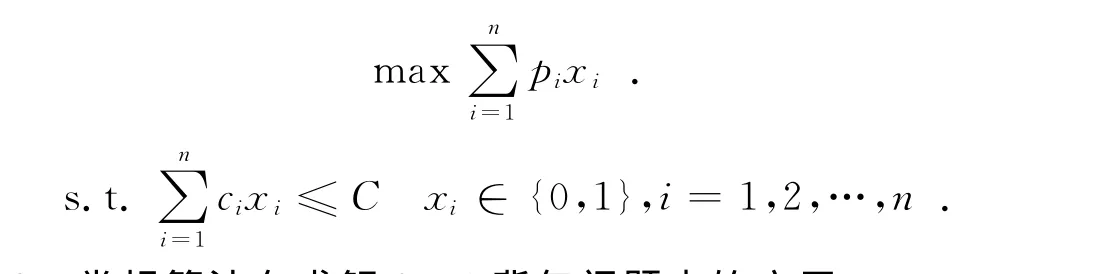關于0-1背包問題的研究*
2014-05-15 08:10:32王雯,武燕
機械工程與自動化
2014年3期
王 雯,武 燕
(太原工業學院,山西 太原 030008)
0 引言
背包問題是一種組合優化問題,具有較強的實際意義,從現實應用角度來看,貨物的裝箱問題、物資的分配和存儲問題等都可以用背包問題來解決。隨著現代網絡的日益發展,在電子商務領域中,背包公鑰密碼的應用也越來越廣泛。但是當求解問題的數量較多時,最優解的求解還是比較困難,所以,對0-1背包問題進行算法研究或改進是一件很有必要的工作。
傳統求解背包問題的方法有近似算法和精確算法,其中,近似算法包括貪婪法、粒子群算法[1]、遺傳算法、蟻群算法[2]等;精確算法包括回溯法、動態規劃法等。精確算法存在空間及時間復雜性的問題,為克服此缺點,用近似算法求解背包問題已經越來越受到人們的關注。除了上述這幾種常見的算法以外,還出現了二進制差異演化算法[3]、知識進化算法[4]等新的算法。還有粗糙集也可以用于解決背包問題,將粗糙集理論引入遺傳算法來解決背包問題,目的在于提高單純遺傳算法的搜索效率,同時也可以改善解的質量。
1 0-1背包問題[5]
背包問題可以這樣理解:假設一位商人有一個容量為C公斤的背包,現在有n個重量和價值分別為ci>0和pi>0(i=1,2,…,n)的物件,選擇哪幾個物件放入背包,能使所裝物件的價值最大,并且不超過背包的容量限制。
0-1背包問題是指每類物件都有一件放入或者不放入。設變量為xi,當物件i被放入時,則xi=1;不放入時,xi=0。其數學表達式為: