平板形目標的量子雷達散射截面計算

林 云

(電磁散射重點實驗室,上海 200438)

平板形目標的量子雷達散射截面計算

林 云

(電磁散射重點實驗室,上海 200438)

介紹了一種可以用于平板形目標的基于解析光子波函數的量子雷達散射截面計算方法。與之前相關研究中提出的方法相比,該方法避免了在球面上對一個劇烈變化的積分核的數值積分。該方法數值效率比相關文獻中給出的方法高,并且可以用于任意形狀的理想導體平板的量子雷達散射截面的仿真。

量子雷達；雷達散射截面；光子波函數

0 引言

近年來,量子信息科學的分支量子通信和量子計算得到了長足的發展。處于量子糾纏態的微粒被用于保密通信;具有350個量子比特的量子計算機已被實現［1］。Shor算法和Grover算法等量子算法展現出比傳統算法更高的效率［2,3］。這些量子信息科學的最新進展也為量子探測的發展奠定了基礎。將糾纏態微粒使用在雷達系統中,從而實現一部雷達同時工作在多模式下的想法是量子雷達的最初概念［4］。量子雷達的概念提出至今不到十年時間,實現中還有很多問題需要研究。比如量子雷達的系統構成、其發射機和接收機的設計、信道描述和信號處理方法、散射截面分析方法等。其中,量子雷達散射截面的研究與其系統實現無關,而且是系統設計的重要輸入參數,急需深入研究,但目前相關的研究較少。

2012年,美國ITT公司的Marco在文獻［5,6］中給出了量子雷達散射截面的定義,并且從定義出發給出了一種可以實現的算法。采用該方法Marco給出了矩形理想導體平板的量子雷達散射截面的數值計算結果,但該方法由于需要在球面上計算一個劇烈變化的積分核的數值積分,計算效率較低,僅用于很小的系統量子雷達散射截面的模擬。

本文利用光子波函數和量子雷達散射截面的定義推導了量子散射截面的計算公式。相比于已有文獻中給出的計算方法,本方法有更高的計算效率。通過量子雷達散射截面的數值算例,討論了本算法的正確性和有效性。

1 理論及公式

與傳統的雷達散射截面類似,量子雷達散射截面σQ可以定義為目標在量子化的電磁場照射下的散射場強度和入射場強度的比值,并用球面波擴散因子歸一化［5］。

其中:

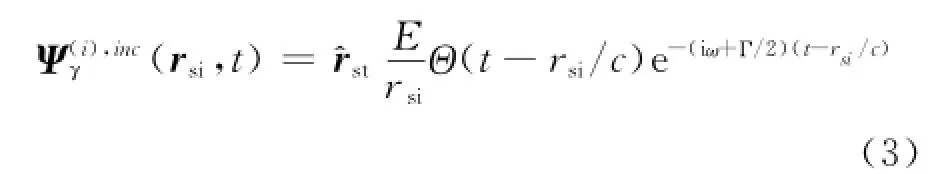
同理,利用光子波函數的定義,散射場強度可表示為

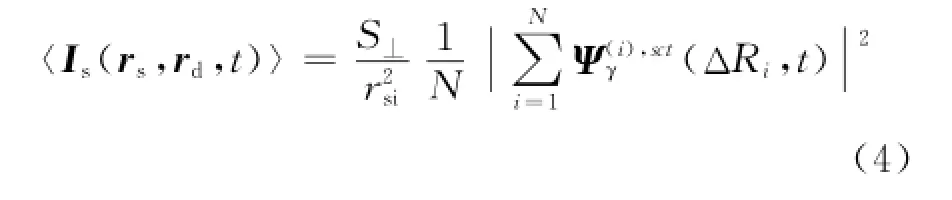
其中:

式中:S⊥為目標垂直于入射方向的表面積;為散射場光子波函數;ΔRi為目標與雷達之間的來回總路程;為目標指向雷達的單位矢量。

量子雷達散射截面σQ可表示為

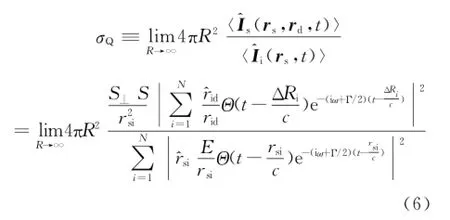
具體推導過程見參考文獻［6］。對于量子雷達散射截面的計算,滿足遠場條件,可用遠場條件rid≈rsi≈R對式(6)進一步簡化,得

文獻［5］中給出的量子雷達散射截面的計算式為

比較式(7)與式(8),可以發現式(8)中分母部分是一個劇烈變化的積分核在球面上的數值積分。該積分的計算需要非常多的積分點才能獲得良好的精度,這意味著需要大量的計算時間。而采用式(7)則可以避免這個問題,從而加快計算的速度。而且文獻［5］中僅僅給出了矩形平板的量子雷達散射截面的數值結果,而式(7)則可以適用于任意形狀的平板結構的量子雷達散射截面的仿真。

2 數值算例

用幾個數值算例來分析本文提出的算法的正確性和高效性。首先為了驗證程序的正確性,用本文提出的算法計算了一個理想導體矩形平板的單站量子雷達散射截面。該矩形平板的尺寸長為4λ,寬為2.5λ,(λ為入射光子的波長,文中取1 m)。該矩形平板用100 000個微粒模擬,具體的設置如圖1所示,該理想導體平板處于xoy平面,入射面為yoz平面,入射光子的傳播方向與z軸的夾角為θ。

圖1 理想導體平板的單站雷達散射截面示意圖

采用文中給出的方法計算該理想導體平板的量子雷達散射截面,數值結果如圖2所示。

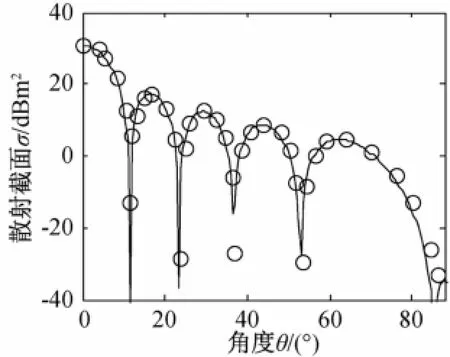
圖2 矩形平板的單站量子雷達散射截面

由圖2中可以看出采用本文給出的方法得到的計算結果(實線)和文獻［6］中給出的結果(圓圈所示)吻合較好。在計算速度方面,這個算例是在一臺配置了Intel 3.0 GHz CPU的臺式微機上完成仿真的,計算總耗時僅5.6 s。而據文獻［6］中的報道,在一臺Intel 1.4 GHz CPU的電腦上仿真一個由單光子和10 000微粒構成的量子系統,耗時約4 h。由此可見,本算法大大加快了量子雷達散射截面的仿真速度,提升了對復雜量子系統仿真的能力。

由圖3中可以看出,金屬平板的量子雷達散射截面(實線)和傳統雷達散射截面(十字所示)的趨勢相似,但在副瓣位置出現較大的區別。

圖3 單站量子雷達散射截面與量子雷達散射截面比較

本文給出的方法可以用于任意形狀的理想金屬平板的量子雷達散射截面的仿真。為驗證這一點,將測試橢圓形理想導體平板的量子雷達散射截面。該橢圓平板的長半軸為20λ,短半軸為10λ。考慮單光子入射情形的單站量子雷達散射截面。仿真的結果如圖4所示,傳統雷達散射截面是通過物理光學方法獲得的。

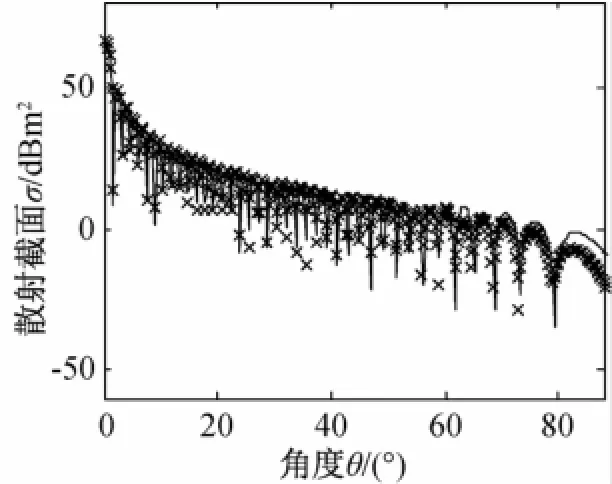
圖4 橢圓形平板的雷達散射截面

3 結論

本文基于量子雷達散射截面和光子波函數的定義推導給出了一種可以快速有效計算量子雷達散射截面的方法。利用該算法成功求解了矩形及橢圓形理想金屬平板的量子雷達散射截面,具有良好的數值精度和較高的計算速度。

［1］Peter W.Shor.Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quanturn Computer［C］.Proceeding of the 35th Annual Symposium of Foundations of Computer Science,IEEE Computer Society Press,1994:124-134.

［2］L.Grover.Quantum Mechanics Helps in Searching for a Needle in a Haystack［J］.Physics Review Letter,1997,79(23):325-328.

［3］E.H.Allen,M.Karageorgis.Radar Systems and Methods Using Entangled Quantum Particles［R］. US Patent 7375802,2008.

［4］Marco Lanzagorta.Quantum Radar［M］.USA: Morgan&Claypool Publishers,2011.

［5］Marco Lanzagorta.Quantum Radar Cross Sections［J］.Proceedings SPIE,Quantum Opics,2010, 7727.

［6］Yun Lin,Liangshuai Guo,Kun Cai.An Efficientalgorithm Fir the Caculation of Quantuam Radar Cross Section of Flat Objects［C］.PIERS,PIERS Proceeding,2014: 39-43.

Calculation of Quantum Radar Scattering Cross Section of Flat Structures

LIN Yun
(Science and Technology on Electromagnetic Scattering Laboratory,Shanghai 200438,China)

This paper proposed an alternative way for simulation quantum radar scattering cross section of flat objects.The presented method is based on the analytical photon wave function.Compared with previous studies,the presented method avoids the evaluation of an integral of a rapid changing pattern on a spherical surface.Thus the proposed method is more computational efficient,and is able to simulate the quantum radar cross section of arbitrary shape flat structures.

quantum radar;radar scattering cross section;photon wave function

TN011

A

1671-0576(2014)04-0050-04

2014-08-13

林 云(1981―),男,博士,工程師,主要從事計算電磁學研究。