電能計量設備檢定中心智能立庫調度優化研究

孫衛明 方彥軍 肖勇 唐猛

(廣東電網公司電力科學研究院1,廣東 廣州 510000;廣東省智能電網新技術企業重點實驗室2,廣東 廣州 510080;武漢大學動力與機械學院3,湖北 武漢 430072)

電能計量設備檢定中心智能立庫調度優化研究

孫衛明1,2方彥軍3肖勇1,2唐猛3

(廣東電網公司電力科學研究院1,廣東 廣州 510000;廣東省智能電網新技術企業重點實驗室2,廣東 廣州 510080;武漢大學動力與機械學院3,湖北 武漢 430072)

為有效解決電能計量設備檢定中心智能立體倉庫的出入庫作業調度優化問題,提出了一種改進的人工魚群算法(AFSA)。針對系統出入庫作業的特點,設計了一種包含軌道引導小車(RGV)的升降機在各階段選擇信息的編碼和解碼方法。將記憶行為和個體交流行為引入算法,并采用自適應步長和視野范圍來避免算法陷入局部最優,加快算法的后期收斂速度。結果表明,該改進算法收斂速度更快、優化率更高、得到的解最優,具有較強的實用性和魯棒性。

智能立體倉庫 電能計量 升降機 人工魚群算法(AFSA) 調度優化

0 引言

智能立體倉庫是存放電能計量設備的主要載體,也是檢定中心的重要組成部分,其運行效率直接影響檢定中心的整體效率[1-2]。因此,提高智能立體倉庫的運行效率是提高檢定效率的關鍵。

對于自動小車存取系統(autonomous vehicle storage and retrieval system,AVS/RS)的軌道引導小車(rail guided vehicle,RGV)調度問題,羅鍵等[3]提出了一種基于改進量子微粒群的優化方法,但未對升降機的選取進行討論。吳長慶等[4]提出了一種基于Petri網和有向圖的死鎖控制方法,但系統中只含有一臺升降機。目前,對于多RGV多升降機AVS/RS系統的存取調度問題鮮有人研究。

本文給出了AVS/RS系統的出入庫作業調度數學模型,并運用改進的人工魚群算法(artificial fish swarm algorithm,AFSA)求出該模型的最優解,從而得到系統的最優調度策略。

1 AVS/RS系統調度問題描述與建模

1.1 問題描述

多升降機AVS/RS系統的調度優化問題,即當系統中有任務觸發時,為每個RGV規劃運行路徑。與平面AGV系統不同的是:RGV在執行跨層作業時,系統不僅需要規劃水平路徑,還要對其垂直路徑進行規劃,即選擇合適的升降機來完成垂直方向上的運動,以提高系統整體的運行效率。

AVS/RS系統主要包含入庫作業、出庫作業兩種作業類型。入庫作業是指RGV將單位負載從其所在貨位運至出入庫(I/O)口,出庫作業是指RGV將單位負載從出入庫口(I/O)運至其分配貨位。對于上述兩種作業類型,RGV執行一次操作時需要經過兩個運行過程:一是RGV從當前位置運行至單位負載所在位置完成裝載;二是RGV從該單位負載所在位置運行至其目標位置完成卸載。兩種操作的運行過程示意圖如圖1所示。系統在進行單位負載的出入庫作業調度時,RGV按照分批作業的方式進行,即將所有任務按照RGV數量分為若干批,然后進行循環作業。

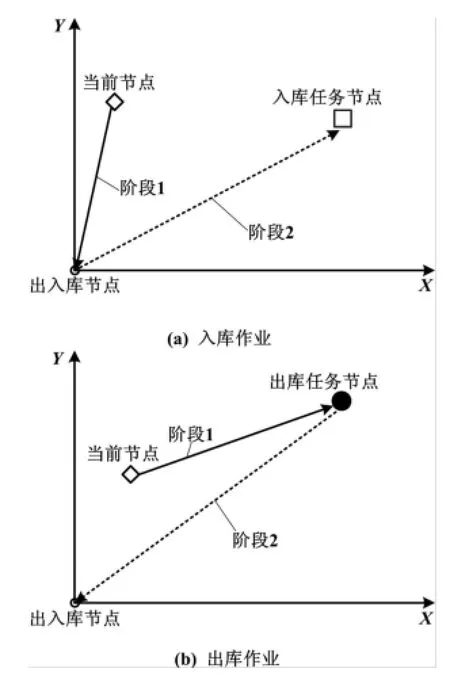
圖1 RGV作業平面示意圖Fig.1 Schematic diagram of the RGV job plane

對于大多數任務而言,至少有一個階段需要借助升降機來實現垂直方向上的運動。當系統完成任務分配后,需要對各RGV各階段的路徑進行規劃。水平路徑是由垂直路徑所決定的。為提高整體存取效率, RGV的路徑規劃需考慮升降機的調度。因此,RGV各階段的水平路徑及升降機的選擇(垂直路徑)是系統調度優化的關鍵。

1.2 問題的轉化

RGV在執行出入庫作業時,其每一階段都包括水平方向上和垂直方向上兩個部分的運動路徑。

水平方向上的運動路徑包括以下兩方面內容。

①水平方向上的運動路徑

一是RGV從當前位置至升降機所在位置的運行距離dhk1;二是RGV出升降機至到達目標節點的運行距離dhk2。水平方向上的運行時間為Dhk=dhk1+dhk2。

②垂直方向上的運動路徑

在多RGV多升降機AVS/RS系統中,從系統的運行成本考慮,RGV的垂直運行路徑應由電梯的空跑距離和RGV實際搭乘電梯的距離組成。選擇不同的升降電梯,其垂直路徑也不相同。垂直運行路徑為Dvk=Wd+Rd。其中,Wd為升降電梯從當前位置運行至RGV所在層的距離,即升降機的空跑距離; Rd為RGV從升降機至目標層的運行距離,即RGV的實際搭乘距離。Wd與升降機的當前位置、升降機的狀態等因素有關。

本文將AVS/RS系統中RGV的調度優化問題轉化為不相關并行機的混合流水線調度問題(hybrid flow-shop schedulingproblem,HFSP-UPM)[5-9]。各RGV進行一次出入庫作業時,至少有一個階段需要進行電梯的選擇,把各升降電梯看作不相關并行機。另外,HFSP要求每一階段各工件均要完成一次機器的選擇,但作業過程中會出現某一RGV在某一階段不需要使用升降電梯(非跨層任務)的情況,為此本文添加一個虛擬電梯。選擇虛擬電梯,表明在此階段無需搭乘電梯且垂直運行距離Dvk為0。AVS/RS系統一次作業的示意圖如圖2所示。

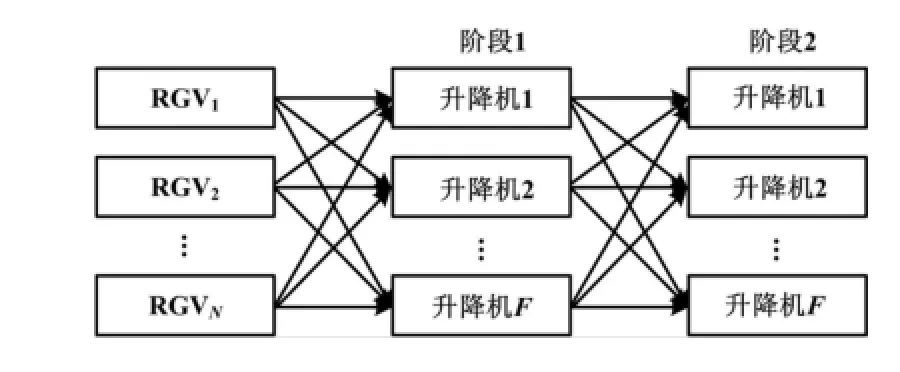
圖2 AVS/RS系統調度示意圖Fig.2 Schematic diagram of AVS/RS system scheduling

1.3 數學模型

綜上所述,多升降機AVS/RS系統的出入庫作業調度優化可視為以路徑長度為優化目標的HFPS問題[8-9],具體描述如下。

設系統當前入庫(出庫)任務為T個,由N個RGV運用(F-1)個升降機進行批組循環作業,且N≥F,將S個任務分為T/N=P(令P為整數)個批組進行循環作業。每個循環中的作業組數量為N,每個批組需經歷兩個階段。令每階段的并行升降機個數為F,其中有一個為虛擬升降機,記RGV的編號為b(b=1,2,…, N)。每一階段RGV可選擇任意升降機到達其目標層,同一RGV選擇不同的升降機所經歷的路徑不同。因此尋找一個完成所有任務距離最短的作業方案I為優化目標,則目標函數為:

式(1)為調度優化指標,其中,Ds,b,hk1為該RGV從當前位置運行至升降機f所在位置的運行距離, Ds,b,hk2為該RGV從升降機當前位置運行到目標貨位的運行距離。式(2)為第b個RGV在階段s選擇升降機f的垂直運行距離,包括升降機f從當前位置到達該RGV所在層的運行距離Ws,b,f及該RGV實際搭乘升降機的運行距離Rs,b,f。式(3)為各階段升降機的使用情況。式(4)表示同一階段每個RGV只能占用一臺升降機。

2 改進的人工魚群算法(IAFSA)

2.1 基本人工魚群算法

基本人工魚群算法(AFSA)是首先構造簡單的人工魚模型,然后通過模擬魚群覓食、聚群、追尾等食物搜索行為,并將每一代的最優解計入“公告板”,最終實現問題尋優的群智能優化算法。人工魚的狀態定義為X= (x1,x2,...,xn),X為欲尋優的變量,n表示向量X的維度。人工魚當前所在位置的食物濃度定義為Y=f(X), Y表示適應度函數值。AFSA算法中,dij=||Xi-Xj||表示個體之間的距離,V為人工魚的視野范圍,S為人工魚的最大可移動步長,δ為擁擠度因子[10]。

雖然AFSA算法善于利用全局信息,具有較強的全局搜索能力,但由于擁擠度的作用,使得個體始終無法集結到最優值附近,從而導致后期的收斂速度較慢且容易陷入局部極值點。

2.2 改進算法

目前已經出現一些人工魚群的改進算法,如運用粒子群算法對人工魚群算法進行優化[11]、增加魚群的跳躍行為[12]等。本文將記憶、個體交流兩種行為引入人工魚群算法,同時采用自適應步長和視野范圍,以此來提高算法的后期收斂速度和避免其陷入局部最優。

2.2.1 記憶行為和個體交流行為

①記憶行為

記憶行為指人工魚Xi向自身所經歷的最優位置Xi|best移動一步。該行為使人工魚在決定下一步的移動方向時能夠參考自身所經歷過的最優位置,增強了魚群行為的方向性。

②個體交流行為

個體交流行為指人工魚Xi向魚群公告板上記錄的最優位置Hbest移動一步。該行為使人工魚在決定下一步移動方向時能夠參考整個魚群的最優位置,增強了魚群搜索過程中個體間的信息交流與共享。

2.2.2 自適應步長和視野范圍

為了增強算法的全局及局部搜索能力和優化精度,人工魚在初期采用較大的視野范圍及步長進行大范圍搜索。在算法的后期,通過逐步縮小視野范圍及步長在最優值附近進行局部搜索,以此來提高算法的局部搜索能力和尋優精度。

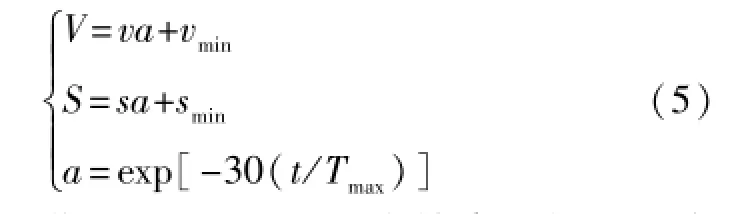
式中:初始視野范圍V=Zm/4,Zm為搜索空間的最大值;S=V/8;t為當前的迭代次數;Tmax為最大迭代次數。

3 AVS/RS系統優化調度

針對AVS/RS系統調度的特點,本節對改進人工魚群算法(improved artificial fish swarm algorithm, IAFSA)中的編碼與解碼、適應度函數進行說明,最后給出算法流程。

3.1 編碼與解碼

根據AVS/RS系統調度模型的特點,采用整數編碼方式表示RGV在各階段所選擇的升降機編號,每階段的并行升降機數量為F。狀態向量Xi構成一條人工魚,人工魚的維度為2N(N為RGV數量)。它包含了系統中RGV及升降機的調度情況,每條人工魚對應一個可行的調度方案。如令一條人工魚的狀態為: Xi={xi1,xi2,…,xiN;xi(N+1),xi(N+2),…,xi(N+N)}={1,4, 3,2,0;3,2,1,4,2},每個字符元素為[0,F]之間的整數,如第三個元素“3”表示在第一階段3號RGV搭乘3號升降機來完成垂直運動。根據約束條件確定RGV在各階段的升降機選擇即稱為解碼。

3.2 適應度函數

本文的優化目標為完成所有任務組的最大運行距離,采用乘冪變換對目標函數進行適度縮小,則適應度函數為:

式中:Lmax為一條人工魚所代表的一個調度方案的最大運行距離。

3.3 適應度函數

AVS/RS調度模型的IAFSA算法流程如下。

①基于AVS/RS調度模型的特點,初始化人工魚群信息,包括各人工魚S、V。

②計算各人工魚適應度值,公告板記錄最優值,根據2.2.2節方法調整人工魚S、V。

③對各人工魚的4種行為(聚群、追尾、記憶和個體交流)進行評價,選擇最優的行為。若個體執行該最優行為后適應度值優于當前位置,則執行該行為;否則重新進行行為選擇。

④計算各人工魚適應度值,更新公告板,調整人工魚S、V,判斷是否達到最大迭代次數。若達到最大迭代次數,則輸出最優解;否則轉至步驟③。

4 實例

以某省級電力公司電能計量設備檢定中心智能立體倉庫為例。系統包含RGV數量N=4臺,升降機數量F=4臺,貨架長18 m,高16.5 m;共有6排貨架,單層每面有13個貨位,每排23層,共10 764個貨位;單元貨位高度h=0.45 m,寬度w=0.7 m,深度d=0.5 m。RGV的水平速度Vx=2 m/s,升降機的速度Vy=1.5 m/s。為了驗證改進的AFSA算法求解該問題的有效性,隨機生成一個包含4個貨位點的作業組,分別用基本AFSA算法、量子粒子群優化算法(quantum particle swarm optimization,QPSO)算法[1]與本文提出的IAFSA算法進行實例仿真比較。其中,設初始群體規模A=150,維數為10,最大迭代次數為maxk=160,3種算法各獨立運行20次,得到的平均收斂過程曲線如圖3所示。

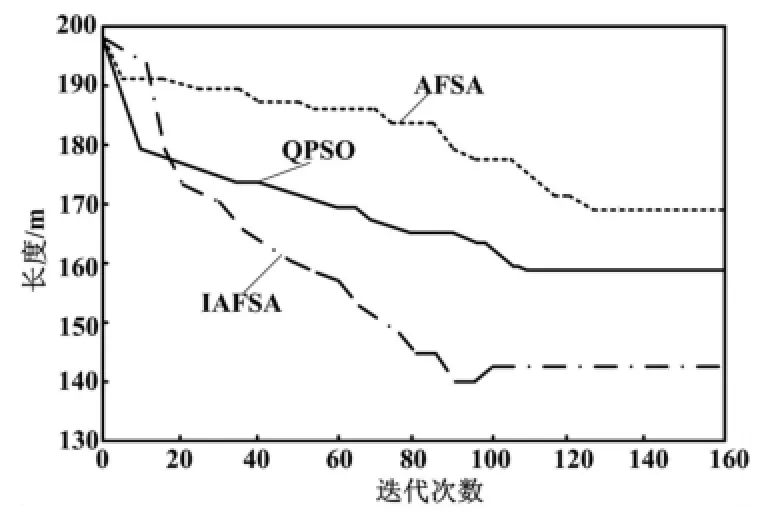
圖3 3種算法的收斂過程曲線Fig.3 The convergence process curves of three of the algorithms

由圖3可以看出,本文提出的IAFSA算法由于采用自適應步長和視野范圍,既能夠避免陷入局部最優,又加快了后期收斂,大約經過100代就能趨于收斂,得到的結果最優。

4個貨位采用3種算法獨立運行20次后結果比較如表1所示。

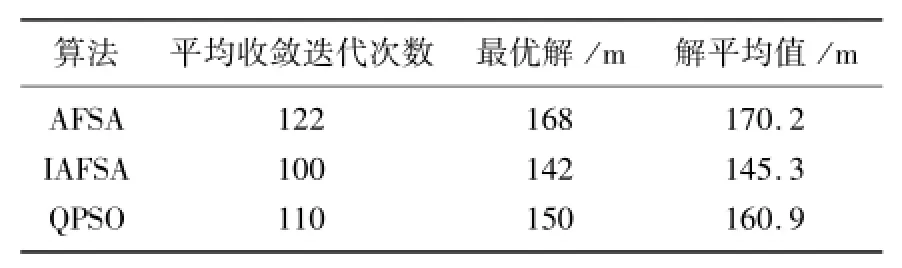
表1 4個貨位的算法結果比較Tab.1 Comparison of the results of algorithms in 4 cargo spaces

從表1可以看出,在相同種群規模和迭代次數的前提下,本文提出的IAFSA算法具有收斂速度快、最優解較好的優點,適合本模型的尋優。

5 結束語

針對AVS/RS系統存取作業調度問題的特點,本文首先對該系統優化調度問題進行詳細分析并建立相應的數學模型。針對該模型的特征,提出了一種改進的人工魚群算法來進行求解。然后設計了一種包含RGV的升降機在各階段的選擇信息的編碼和解碼方法;分別將記憶行為與個體交流行為引入人工魚群算法,并采用自適應步長和視野范圍來避免算法陷入局部最優,同時提高算法的后期收斂速度。最后,以某省級電能計量設備自動檢定中心的AVS/RS系統為例,將該算法與另外兩種算法進行比較。結果表明,該改進算法收斂速度更快、優化率更高,得到的解最優,有效性和魯棒性較強,能夠為AVS/RS系統的調度優化提供理論依據。

[1] 林乃瑜,林岳凌,譚振豪,等.電能表自動加封系統在計量檢定流水線上的應用[J].廣東電力,2013,26(11):122-127.

[2] 梁洪浩,丁國茂.面向未來電網的計量自動化系統存儲技術研究[J].廣東電力,2012,25(4):22-26.

[3] 羅鍵,吳長慶,李波,等.基于改進量子微粒群的軌道引導小車系統建模與優化[J].計算機集成制造系統,2011,17(2):321-328.

[4] 吳長慶,何善君,羅鍵,等.自動小車存取系統中軌道引導小車環路死鎖控制的研究[J].計算機集成制造系統,2008,14(9): 1767-1773.

[5] 王凌,周剛,許曄.求解不相關并行混合流水線調度問題的人工蜂群算法[J].控制理論與應用,2012,29(12):1551-1557.

[6] Pan Q K,Tasgetiren M F,Suganthan P N,et al.A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J].Information Sciences,2010,181(12):2455-2468.

[7] 王圣堯,王凌,許曄.求解相同并行機混合流水線車間調度問題的分布估計算法[J].計算機集成制造系統,2013,12(6):51-15.

[8] Wang X,Tang L.A tabu search heuristic for the hybrid flow-shop scheduling with finite intermediate buffers[J].Computers& Operations Research,2008,36(3):907-918.

[9] Alaykyran K,Engin O,Doyen A.Using ant colony Optimization to solve hybrid flow shop scheduling problem[J].International Journal of Advanced Manufacturing Technology,2007,35(5/6):541-550.

[10] 陳鐵梅,羅家祥.帶擾動和變異因子的改進禁忌搜索算法求解貼片機過程優化[J].控制與決策,2013,28(3):363-368.

[11] 段其昌,唐若笠.粒子群優化魚群算法仿真分析[J].控制與決策,2013,28(9):1436-1440.

[12] Tsai H C,Lin Y H.Modification of the fish swarmalgorithm with particle swarm optimization formulation and communication behavior[J].Applied Soft Computing,2011,11(8):5367-5374.

Research on the Scheduling Optimization of Intelligent 3D Warehouse in Electric Energy Metering Equipment Test Center

In order to effectively solve the problem of scheduling optimization for IN/OUT of storage jobs in intelligent 3D warehouse for electric energy metering equipment test center,the improved artificial fish swarm algorithm(AFSA)is proposed.In accordance with the features of IN/ OUT jobs in the system,the encoding and decoding method is designed,in which the lifter selection information for rail guided vehicle(RGV) at each stage is contained.The memory behavior and individual communication behavior are introduced into the algorithm,and local optimization of the algorithm is avoided by adopting adaptive step and vision field,in addition,the late convergence is speedup.The result shows that this improved algorithm offers faster convergence speed and higher optimized rate and gets optimum solution,possesses stronger practicality and robustness.

Intelligent 3D warehouse Electric energy metering Lifter Artificial fish swarm algorithm(AFSA) Scheduling optimization

TP18

A

國家自然科學基金資助項目(編號:61170024);

中央高校基本科研業務費專項資金資助項目(編號:121031);

廣東電網公司電力科院研究院基金資助項目(編號:K-GD2013-0470-001);

廣東省智能電網新技術企業重點實驗室基金資助項目(編號:2060299)。

修改稿收到日期:2014-03-27。

孫衛明(1971-),男,1994年畢業于華中理工大學電磁測量及其儀表專業,獲學士學位,高級工程師;主要從事電能計量及計量自動化的研究。