重載鐵路貨車副構架式徑向轉向架輪軌動力作用研究
羅漢江 李志強 吳暢 尹買云 李冬 張顯鋒




摘要:本文簡述了評價鐵路貨車輪軌動力作用的主要指標,研究了配裝轉K7型、DZ3型轉向架時車輛輪軌動低動力作用情況。其次,闡述了配裝DZ3型轉向架車輛線路動力學試驗的部分輪軌動力作用試驗結果。結果表明,H.H.Jenkins簡化模型、車輛-軌道耦合動力學模型計算結果相近;車輛各輪軌低動力作用指標均與車輛運行速度呈近線性、正比例關系;與25t軸重轉向架相比,在重載鐵路運輸中DZ3型轉向架具有十分突出的優勢。
關鍵詞:重載鐵路貨車;副構架式徑向轉向架;輪軌動力作用;25t軸重轉向架;DZ3型轉向架
中圖分類號:U270.3 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號:1674-957X(2021)07-0001-04
0 ?引言
重載與高速是鐵路運輸永恒不變的發展主題。2005年,在巴西舉行的國際重載協會(International Heavy Haul Association,簡稱IHHA)的年會上對貨物列車重載運輸的概念重新進行了定義:①重載貨車牽引噸位大于或等于8000t;②軸重大于或等于27t;③在長度大于或等于150km的鐵路區段上運行,每年貨運量大于或等于4000萬t。滿足上述任意兩項,即可稱為重載運輸。
截至目前,我國已有多條重載運輸線路,如大秦鐵路、瓦日鐵路、浩吉鐵路等,其中大秦鐵路和瓦日鐵路則具有較為特殊的意義。大秦鐵路是我國第一條雙線電氣化重載單元列車運輸專線,全長653km,重載列車牽引重量至少可達2萬t,2018年年貨運量突破4.51億t,其主要運用車輛為80t級專用敞車(配裝25t軸重轉向架);瓦日鐵路則是我國第一條按照30t軸重標準建設的重載鐵路,全長1260km,重載列車牽引重量可達1萬t,年貨運量可達2億t,主要運用車輛為80t級通用敞車(配裝27t軸重轉向架)。重載運輸中的鐵路貨車所采用的轉向架均具有低動力、低磨耗、低阻力等特點,而副構架式徑向轉向架是其中的典型代表之一。
國外研究表明,采用徑向轉向架可以有效降低輪軌動作用力,延緩重載運輸中輪軌損傷和磨耗,延長輪軌的使用壽命。其中,可使輪軌橫向力降低10~30%,輪軌垂向力降低約3~5%[1];使輪對沖角降低60~80%,增加車輪壽命500%,增加鋼軌壽命25倍,減少車輛維修70%;曲線通過阻力僅為傳統三大件轉向架的30~50%,能耗可降低5%[2]。為進一步分析徑向轉向架在重載運輸中的突出特點,本文就國內批量運用的25t軸重轉K7型轉向架、27t軸重DZ3型轉向架(簡稱“轉K7型轉向架、DZ3型轉向架”)時在低動力作用等方面進行了研究。
1 ?輪軌動力作用指標
考察鐵路貨車輪軌動力作用的指標有輪軌垂向高頻作用力P1(簡稱“P1力”)和中低頻作用力P2(簡稱“P2力”)、輪軌橫向力Q、車輛蛇行穩定性(即蛇行運行臨界速度Vcr)、輪軌沖角Ψ、脫軌系數Q/P(P為垂向作用力)、輪重減載率ΔP/P、輪軌磨耗功率Wt和輪軌磨耗指數Wi等。結合輪軌磨耗的不同部位、輪軌力實際作用位置、效果等因素,上述指標可反映不同的磨耗狀態,有必要對其進行進一步論述。
1.1 P1力、P2力
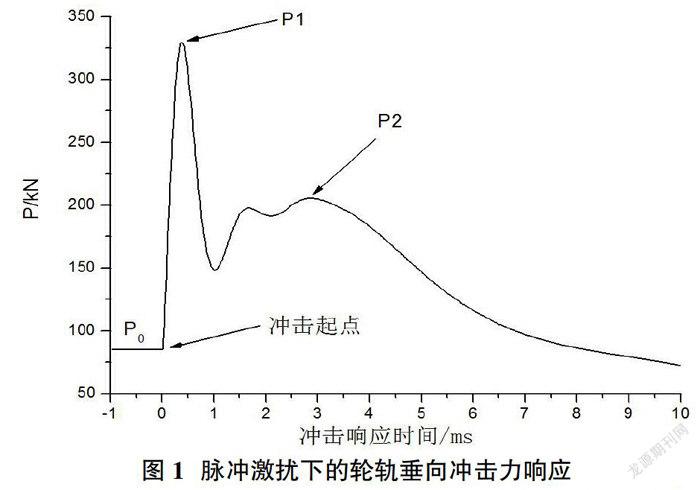
輪軌間的相互作用力包括輪軌間靜態作用力和動態作用力。研究表明,P1力和P2力是評價輪軌垂向動作用力的重要指標,對軌道設施損壞起重要作用,如圖1所示。
P1力是機車車輛簧下零部件與鋼軌間所產生的高頻振動而引起的沖擊力,具有頻率高、衰減快的特點,一般頻率大于500Hz,其來不及向簧上及軌下傳遞,而直接作用于車輪和鋼軌本體上,是導致車輪扁疤、軌道破損、聯接螺栓孔裂紋及魚尾板折斷的主要原因。P2力是整個機車車輛系統與軌道系統受脈沖激勵而出現的中低頻響應力,一般頻率在30~100Hz范圍內,相比P1力,其頻率較低,能夠充分向軌道下部傳遞,對軌道表面狀態及軌下結構起主要破壞作用。
1.2 輪軌橫向力Q、垂向作用力P
車輛在有隨機不平順的線路上運行時,輪軌橫向作用力Q、輪軌垂向作用力P直接作用在車輪和鋼軌之間,是引起鋼軌變形、側翻、橫移、下沉和輪軌磨耗的主要因素。
1.3 輪軌沖角Ψ
輪軌沖角Ψ的大小,既反映車輪爬軌的可能性,又反映輪軌之間的磨耗(特別是車輪輪緣和鋼軌側面磨耗)傾向,也是反映輪軌相互作用的主要指標。
1.4 輪軌磨耗功率Wt、磨耗指數Wi
輪軌間的磨耗功率Wt為輪軌間的蠕滑力與蠕滑率之間的乘積,其單位為kN·m/m,它反映出車輪踏面和鋼軌頂面的磨耗程度,磨耗功率越大,表明車輪踏面和鋼軌頂面的磨損越嚴重。
輪軌間的磨耗指數Wi為輪軌間的橫向力Q與輪軌沖角Ψ的乘積,其單位為kN·rad,它反映出車輪輪緣和鋼軌側面的磨耗程度,磨耗指數越大,表明車輪輪緣和鋼軌側面的磨損越嚴重。
2 ?仿真模型
為研究鐵路貨車輪軌動力作用情況,常用H.H.Jenkins簡化計算模型、車輛-軌道耦合動力學模型、軌道低接頭模型及車輛橫向-垂向耦合動力學模型。同時,在進行P1力、P2力計算時,采用H.H.Jenkins簡化計算模型、車輛-軌道耦合動力學模型兩種模型,以比較兩種結果的差異性。而后的指標則以車輛-軌道耦合動力學模型進行計算。采用軌道為60kg/m軌頭。
根據C80BF(配裝K7型轉向架,簡稱C80BF)、C80EF(配裝DZ3型轉向架,簡稱C80EF)車輛本身的典型結構特點,在建立車輛系統動力學模型時,忽略次要因素,并進行了如下假定:①輪對、U形副構架、側架、搖枕、車體及鋼軌視為剛體;②忽略連掛車輛間的相互作用力,僅考慮單輛車的勻速運行工況。
在車輛動力學建模過程中,針對各剛體、力元、連接元的位置及自身的各向自由度均按照實際車輛狀態進行設置。80t級敞車在橫向、垂向系統共有55個獨立的自由度。計算中車輛的自由度如表1。
根據C80BF、C80EF的車輛結構特點,在對應車輛動力學模型中增加如下非線性因素:①輪軌接觸:在動力學模型中,車輪踏面采用TB 449 《機車車輛車輪輪緣踏面外形》中的LM型車輪踏面,鋼軌型面采用GB 2585 《鐵路用熱軋鋼軌》中的75kg/m鋼軌。②輪軌蠕滑:在研究中先按Kalker小蠕滑線性理論確定蠕滑力,然后采用試探法將所得的蠕滑力修正為滿足要求的非線性值。③車輛懸掛系統:車輛懸掛裝置在工作狀態時,在垂向方向具有兩級剛度特性。在動力學模型中,采用該懸掛裝置的兩級剛度懸掛特性曲線。
摩擦減振器摩擦力的大小與減振彈簧撓度有關,其方向隨側架、搖枕的相對運動速度方向的變化而變化。
在搖枕和車體之間存在回轉摩擦力矩(旁承摩擦力矩、心盤摩擦力矩),其大小、方向車輛空、重狀態及車體搖頭運動有關。
3 ?仿真結果
3.1 P1力和P2力
3.1.1 H.H.Jenkins簡化模型
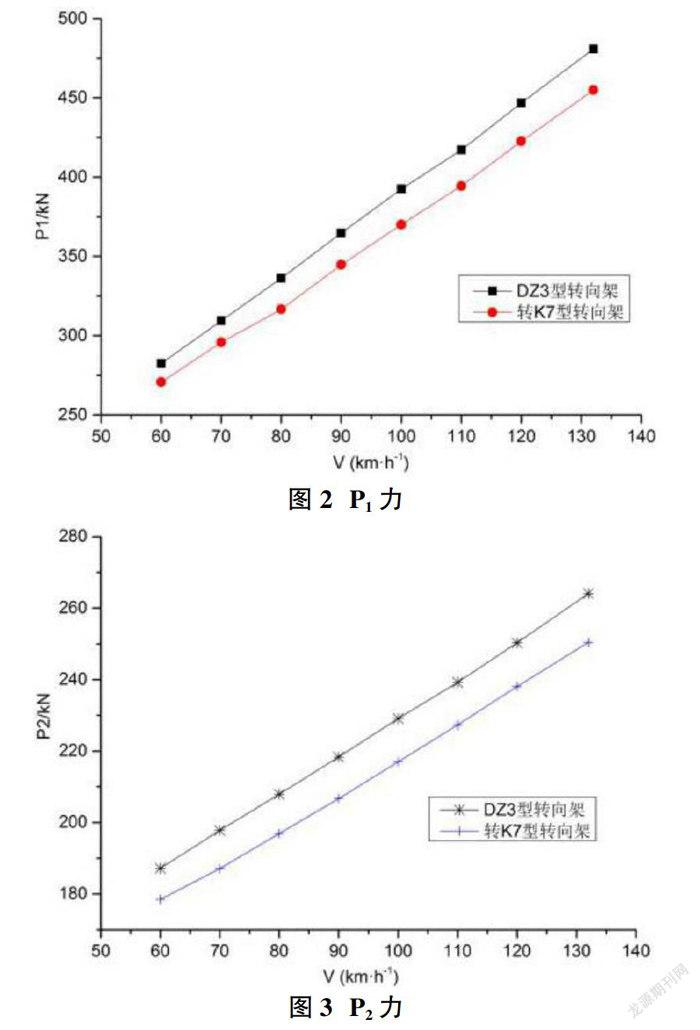
DZ3型轉向架、轉K7型轉向架重車工況在60~132km·h-1速度范圍內,P1力、P2力的計算結果如圖2、圖3。
由圖2、圖3易知,在該模型下,P1力、P2力均與速度V近似呈線性、正比例關系;當車輛運行速度為120km·h-1時,DZ3型轉向架的P1力比轉K7型轉向架的P1力增加5.75%;當車輛運行速度為120km·h-1時,DZ3型轉向架的P2力比轉K7型轉向架的P2力增加5.12%。
3.1.2 車輛-軌道耦合動力學模型
基于車輛-軌道耦合動力學模型,DZ3型轉向架、轉K7型轉向架重車工況在60~132km·h-1速度范圍內,P1力、P2力的計算結果如圖4、圖5。
由圖4、圖5易得,在該模型下,P1力、P2力均與速度V近似呈正比例關系;其次,當車輛運行速度為120km·h-1時,DZ3型轉向架的P1力比轉K7型轉向架的P1力增加5.72%;當車輛運行速度為120km·h-1時,DZ3型轉向架的P2力比轉K7型轉向架的P2力增加6.53%。
另外,對比H.H.Jenkins簡化模型和車輛-軌道耦合動力學模型計算結果后發現,兩種模型下,其結果誤差極小,即當車輛運行速度為120km·h-1時,P1力的誤差值為0.03%;當車輛運行速度為120km·h-1時,P2力的誤差值為-1.41%。這也說明兩種模型可進行相互驗證。如下其余指標將僅按照車輛-軌道耦合動力學模型計算。
3.2 輪軌橫向力Q、垂向力P
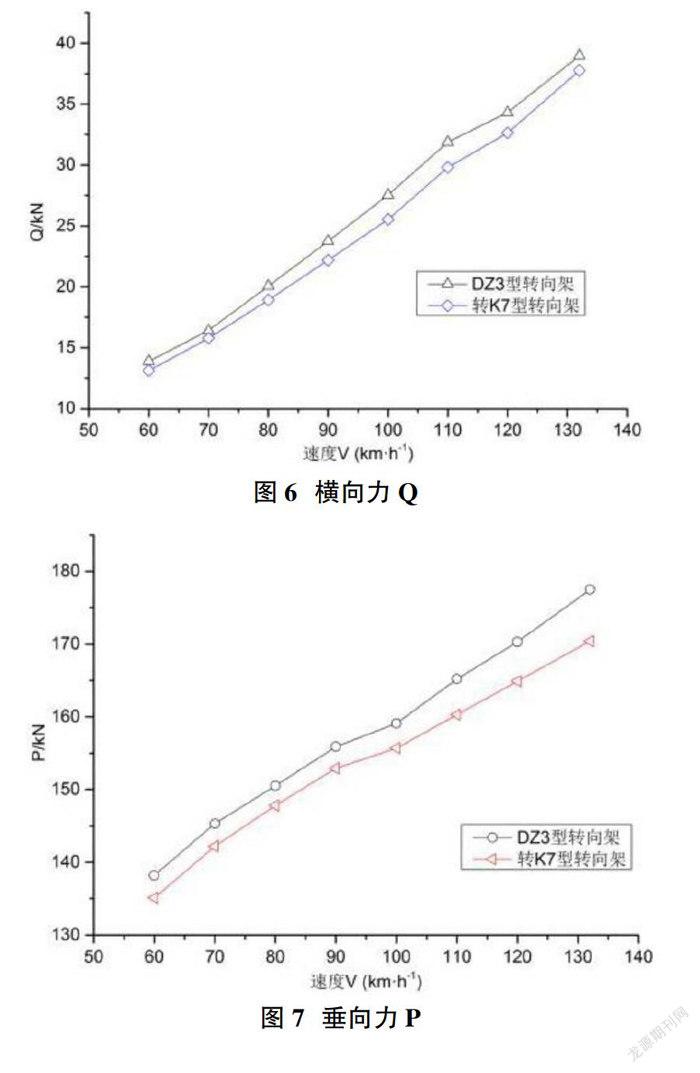
在直線工況、美國Ⅴ級線路譜激擾下,基于車輛橫向—垂向耦合動力學模型,DZ3型轉向架、轉K7型轉向架重車工況在60~132km·h-1速度范圍內,輪軌橫向力Q、垂向力P的計算結果如圖6、圖7。
由圖6、圖7易知,車輛在直線線路運行時,輪軌橫向力的大小與其運行速度近似呈正比關系。當運行速度為120km·h-1時,DZ3型轉向架的輪軌橫向力Q比轉K7型轉向架的輪軌橫向力Q增加5.11%。其次,當車輛運行速度為120km·h-1時,DZ3型轉向架的輪軌垂向力P比轉K7型轉向架的輪軌垂向力P增加3.27%。
3.3 輪軌橫向力Q、垂向力P、輪對沖角Ψ、磨耗功率Wt和磨耗指數Wi
基于車輛橫向—垂向耦合動力學模型,DZ3型轉向架、轉K7型轉向架重車工況通過下列曲線時:
①半徑R=300m、600m、800m,外軌超高h=120mm、90mm、60mm,緩和曲線長度均為LS=75m,圓曲線長度均為LC=100m,最大欠超高均取70mm,運行速度V=69.5km·h-1、90.2km·h-1、93.9km·h-1;②以45km·h-1通過12號道岔組成的過渡線。
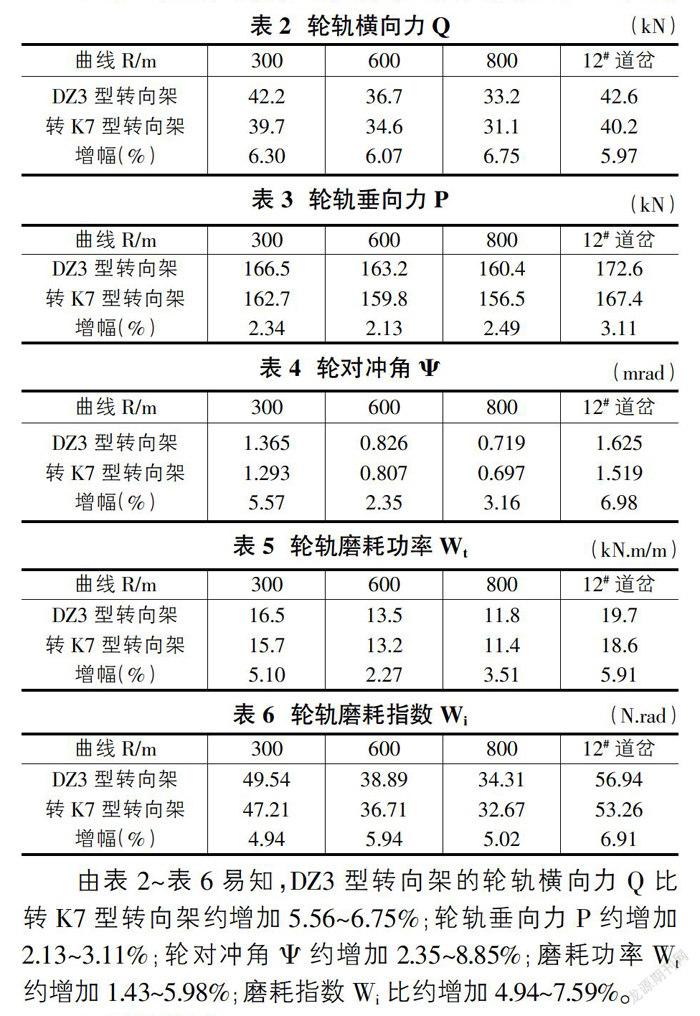
其第一輪對(導向輪對)的相應計算結果如表2~表6。
由表2~表6易知,DZ3型轉向架的輪軌橫向力Q比轉K7型轉向架約增加5.56~6.75%;輪軌垂向力P約增加2.13~3.11%;輪對沖角Ψ約增加2.35~8.85%;磨耗功率Wt約增加1.43~5.98%;磨耗指數Wi比約增加4.94~7.59%。
4 ?試驗結果
2012年9月~2013年6月,鐵道部產品質量監督檢驗中心車輛檢驗站中國鐵道科學研究院對配裝DZ3型轉向架的80t級車車進行了線路動力學試驗。試驗結果表明:在110km·h-1試驗速度范圍內,車輛具有良好的動力學性能,運行平穩性和安全性優于比較車C70型敞車(配裝轉K6型轉向架)。車輛運行穩定性、運行平穩性均符合GB/T 5599-1985《鐵道車輛動力學性能評定和試驗鑒定規范》的要求。試驗車輛及編組如圖8、圖9。
DZ3型轉向架線路動力學試驗輪軌動力作用的部分結果如圖10。由此易知:①車輛以不同速度在直線上運行時,DZ3型轉向架的空車輪軸橫向力最大值和平均值較比較車C70型通用敞車分別降低約13.97~51.04%、39.39~55.10%;重車上述指標分別降低-13.26~22.42%、22.56~51.63%。直線運行時,DZ3型轉向架降低輪軸橫向力效果明顯。②車輛以不同速度通過半徑R350m~R1200m曲線及12號道岔時,DZ3型轉向架的空車輪軸橫向力最大值和平均值較23t軸重的比較車C70型通用敞車分別降低約7.52~57.48%、-8.22~54.33%;重車上述指標分別降低-23.74~41.23%、37.94~41.97%。除個別曲線工況外,DZ3型轉向架曲線輪軸橫向力比23t軸重的比較車C70型通用敞車還小。
5 ?結語
根據以上分析易得:①無論采用H.H.Jenkins簡化模型,還是采用車輛-軌道耦合動力學模型,其計算結果均較為接近,其最大誤差僅為-1.41%,可滿足工程研究之用。②DZ3型轉向架(使用軸重26.375t)的軸重增加5.5%、車輪直徑加大75mm,輪軸重量增加17.2%,轉向架軸距和所配裝的80t級車輛的定距較長,故輪軌作用力有所增加;但從簧下重量增加幅度來講,其仍具有較低的輪軌動力作用指標。③DZ3型轉向架和轉K7型轉向架各低動力作用指標均與速度呈近線性、正比例關系。④和傳統三大件轉向架相比,DZ3型轉向架輪軸橫向力降低幅度明顯、且具有使輪軌橫向力均勻分配的特點,可有效降低輪軌偏磨、側磨,延長其使用壽命。
參考文獻:
[1]嚴雋耄.車輛工程[M].北京:中國鐵道出版社,2004.
[2]嚴雋耄,翟婉明,陳清,傅茂海.重載列車系統動力學[M].北京:中國鐵道出版社,1999.
[3]王福天.車輛動力學[M].北京:中國鐵道出版社,1983.
[4]中國鐵道科學研究院.C80EF型通用敞車(2011年研制)檢驗報告[R].
[5]L.L. Bradfield, R.D. Fr?觟hling. Radially Aligning Self-Steering Bogies an Indispensable Key to Green Heavy Haulage[J]. 10th International Heavy Haul Association Conference, 2013:722-728.
[6]王勇,羅仁,池茂儒.西南交通大學牽引動力國家重點實驗室.大軸重貨車轉向架輪軌動力作用和磨耗研究.
[7]西南交通大學.南車眉山車倆有限公司27t軸重副構架式徑向轉向架輪軌作用力計算報告[R].
基金項目:四川省科技攻關計劃;項目號:2019JDRC0030;項目名稱:具有變摩擦功能的鐵路貨車控制型轉向架性能研究。
作者簡介:羅漢江(1983-),男,甘肅蘭州人,學士,高級工程師,從事轉向架設計工作。

