諧波阻抗和背景諧波電壓 估算方法的對比研究
張 龍 陳西平 李洪杰 劉 斌 孫振權
(1.西安交通大學電氣工程學院,西安 710049;2.陜西省地方電力集團,西安 710061)
電能既是一種經濟、實用、清潔且容易控制的能源形態,又是電力部門向電力用戶提供由發、供、用三方共同保證質量的特殊商品,因此,它同其他商品一樣要講求質量[1]。圍繞電能質量的含義,從不同角度理解一般包括電壓質量、電流質量、供電質量和用電質量[2]。在復雜配電系統中,除了個別大型諧波源負荷能確定其位置,系統中還有許多由不同類型和容量的用電設備按照一定網絡結構組成的綜合諧波負荷。在實際應用中檢測點將受到一定限制,因此通過對公共連接點的測量,尋找出準確、實用的對配電系統諧波源定位和檢測與用戶諧波發射水平的測量方法,制定一套反映系統和用戶對公共連接點諧波污染責任的指標是當務之急[3-6]。
國內外對諧波發射水平的估計方法主要是圍繞對系統側和用戶側諧波阻抗的估算來展開。現有的諧波阻抗估計方法基本可以分為“干預式”和“非干預式”兩大類[7-8]。“干預式”方法主要包括注入法、開關元件法等,通過向系統強迫注入諧波電流或者間諧波電流,或是開斷系統某一支路來測量諧波阻抗。該類方法會對系統運行造成不利影響,因此不能廣泛使用。“非干預式”方法主要包括波動量法、線性回歸法等,利用系統自身的諧波源和可測量參數等來估計諧波阻抗和諧波電壓[9-12]。
本文研究分析了基于獨立隨機矢量協方差特性和基于二元線性回歸這兩種諧波發射水平評估方法的基本原理,利用PSCAD 仿真軟件建立三電壓等級、整流負荷仿真模型,通過Matlab 計算諧波阻抗和背景諧波電壓,進而估算出用戶諧波發射水平。最后,在IEEE 14 節點系統模型中改變負荷類型等條件,對比兩種方法計算諧波阻抗和背景諧波電壓的能力。
1 基本原理
h次諧波等值電路如圖1所示。
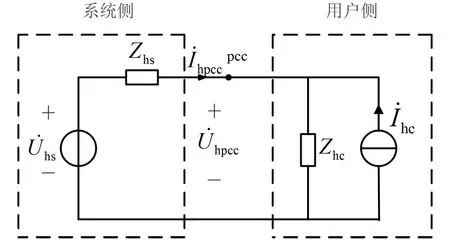
圖1 系統側與用戶側某次諧波等值電路
1.1 基于獨立隨機矢量協方差特性的評估方法
基于獨立隨機矢量協方差特性的諧波發射水平評估方法根據公共連接點處諧波電流與系統背景諧波只有弱的聯系,利用隨機矢量協方差特性抵消偏差量方程中背景諧波變動項,解得系統側諧波阻抗,并跟蹤計算用戶諧波電壓發射水平[13]。
根據等值電路列方程
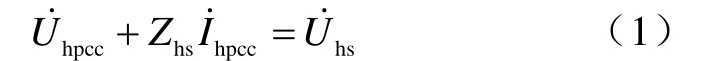
實際系統中,估計時段內(N個樣本點)系統側諧波阻抗基本不變,對式(1)求均值得
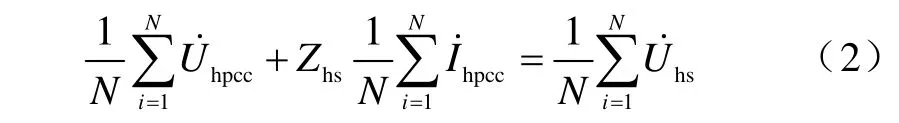
式(1)減式(2)得
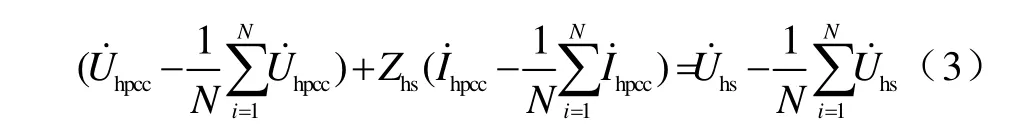
由圖1知
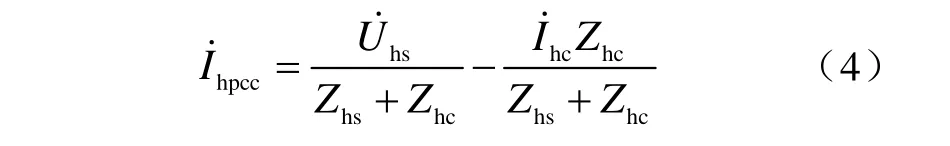

式中,*表示對復數求共軛。
實際計算中,若樣本點足夠多,期望可近似體現為均值,因此式(5)近似為
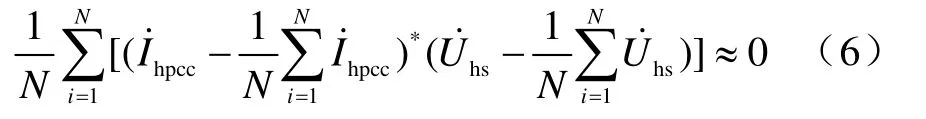
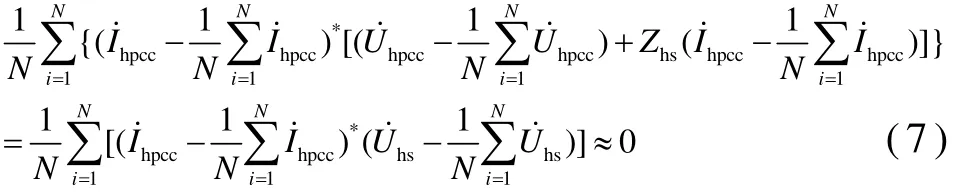
則式(7)變形為
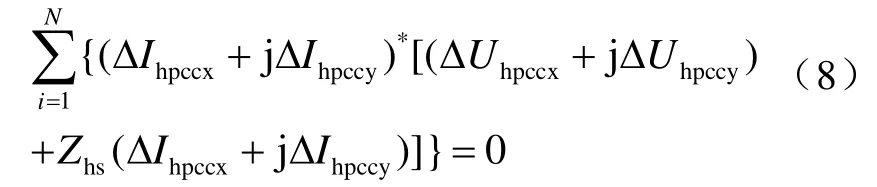
解得系統諧波阻抗實部和虛部分別為
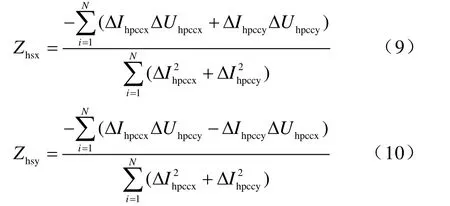
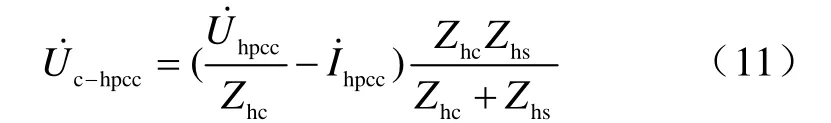

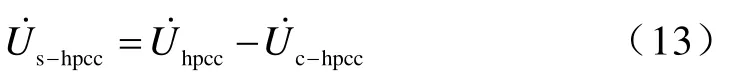
1.2 基于二元線性回歸的評估方法
基于二元線性回歸的用戶諧波發射水平估計方法是在假定系統側基本穩定的條件下,以公共連接點諧波電壓、電流測量參數為觀測數據,根據系統和用戶等值電路推導的二元回歸方程求取系統側諧波阻抗,進而計算用戶諧波發射水平[14]。
根據等值電路列方程
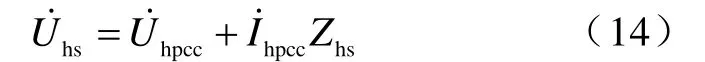
按實部、虛部分開有
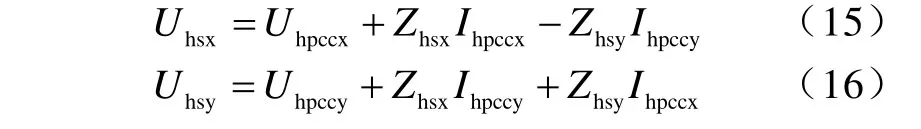
式中,*x為實部,*y為虛部。
由式(16)變換可得
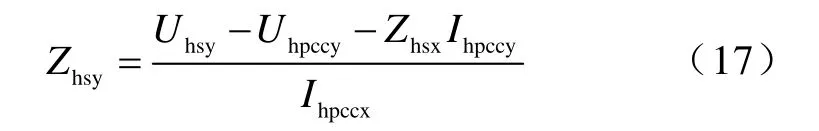
或
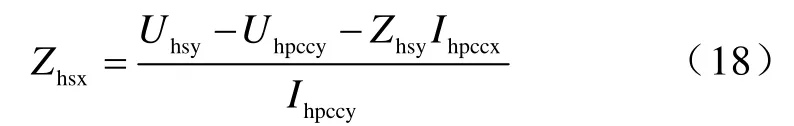
將式(17)代入式(15)整理得
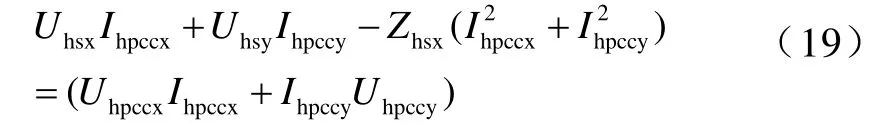
將式(18)代入式(16)整理得
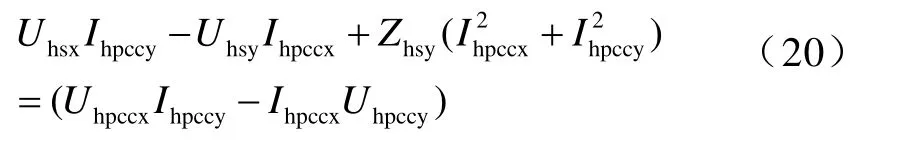
式(19)、式(20)中未知變量分別為Uhsx、Uhsy、Zhsx和Uhsx、Uhsy、Zhsy,根據二元線性回歸分析方法可以由測量值求取它們的估計值。其中,兩對Uhsx和Uhsy作為系統諧波電壓源最小方差估計值,而Zhs=Zhsx+ jZhsy為系統側諧波阻抗。
由圖1和式(14)得
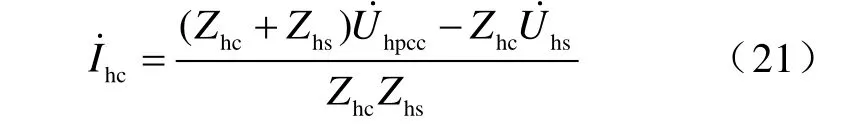
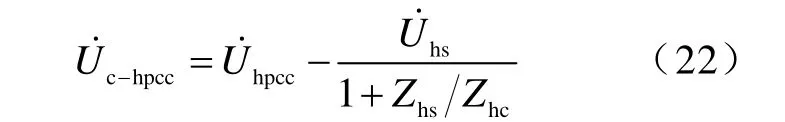
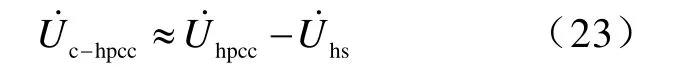
2 仿真分析
2.1 原理模型仿真計算
用PSCAD 根據系統側與用戶側某次諧波等值電路搭建原理仿真模型如圖2所示。
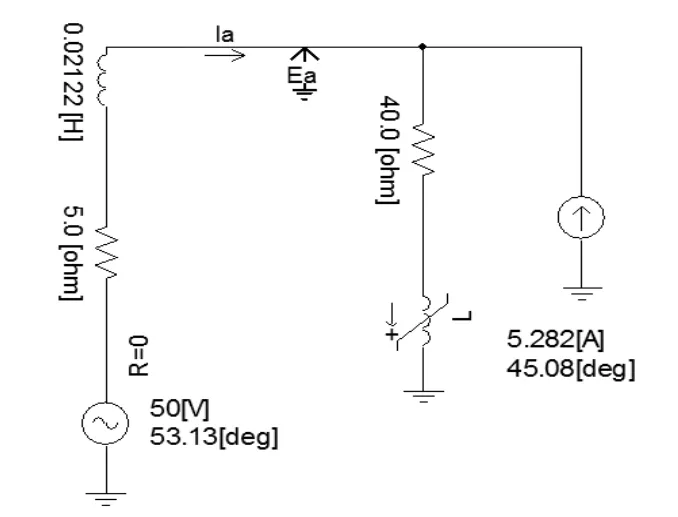
圖2 原理仿真模型
系統頻率為50Hz,元件參數如圖2中所示。系統側等值三次諧波阻抗為5.0+j20.0(Ω);用戶側等值三次諧波阻抗為40.0+j296.0(Ω)。該模型用隨機函數發生器產生在-0.002~0.002 之間隨機變化的數值控制用戶側電抗,模擬系統產生波動,發出諧波。PCC電壓Ea和電流Ia經FFT 處理。設定采樣頻率為4000Hz,測量時間為10 個周波,測量間隔為0.8s。
在PCC 抽樣三次諧波電壓、電流80000 個點的波形數據如圖3所示。分段(20 段,每段4000 個點,測量每段前800 個點,測量間隔為3200 個點)計算所得系統側諧波阻抗如圖4所示。

圖3 PCC 三次諧波電壓幅值和電流幅值的采樣數據
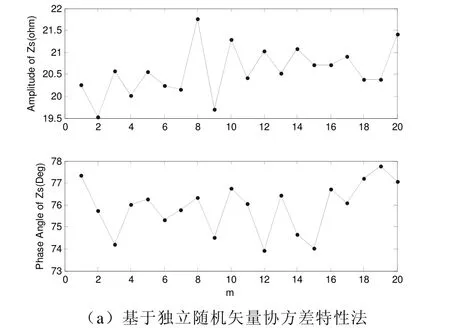
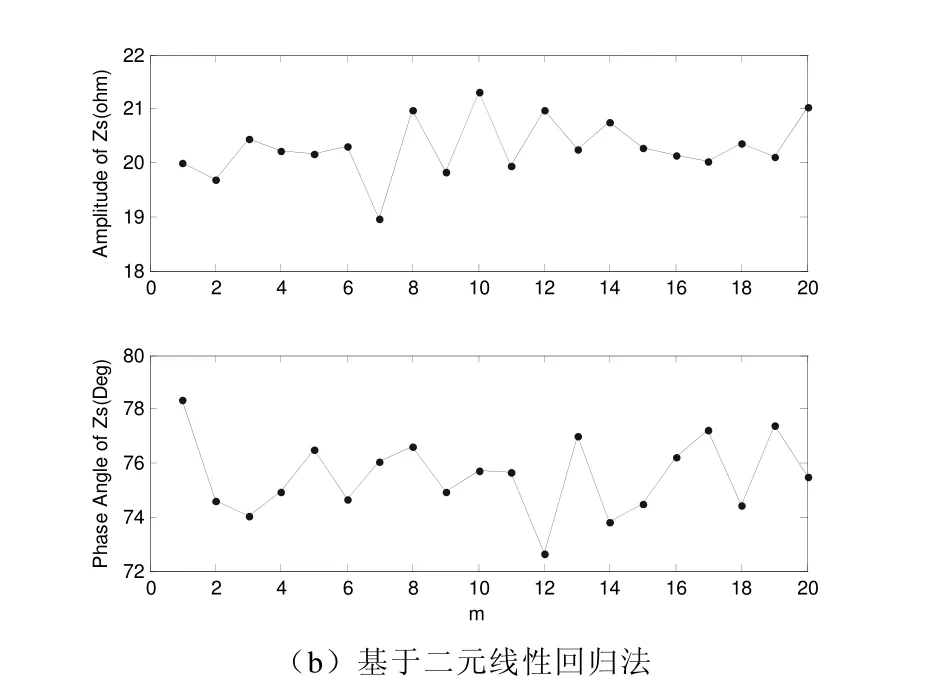
圖4 系統側諧波阻抗
總共16000 個測量點的PCC 電壓幅值Vpcc和按照諧波阻抗重新計算的系統側諧波電壓幅值Vs-pcc如圖5所示。用戶諧波電流在PCC 引起的電壓降幅值Vc-pcc如圖6所示。
兩種方法的計算結果如表1所示,與設定值十分接近,誤差較小,這說明兩種方法在計算系統諧波阻抗和背景諧波電壓中具有可行性、準確性。
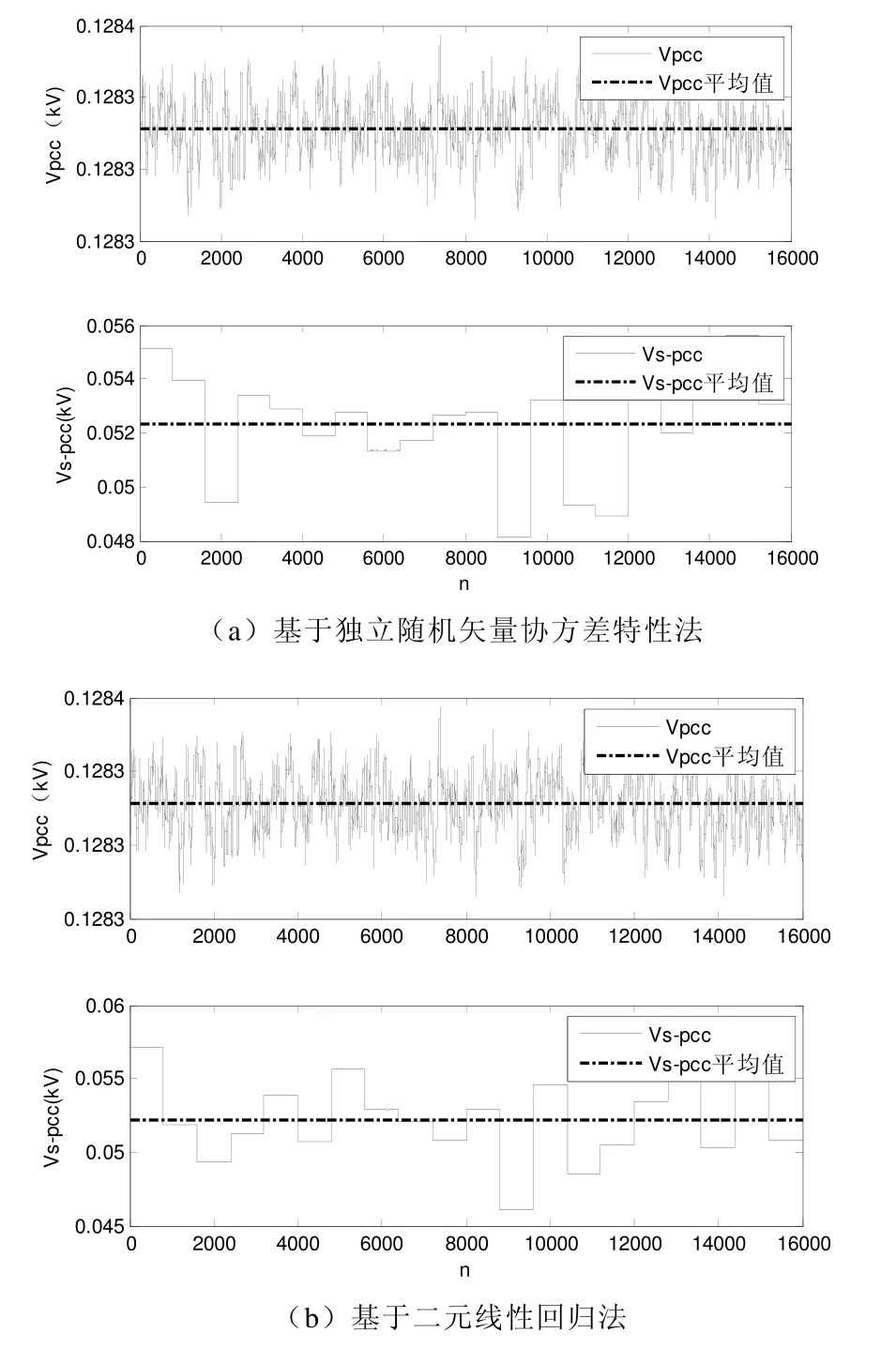
圖5 PCC 和系統側諧波電壓在16000 個測量點的計算值
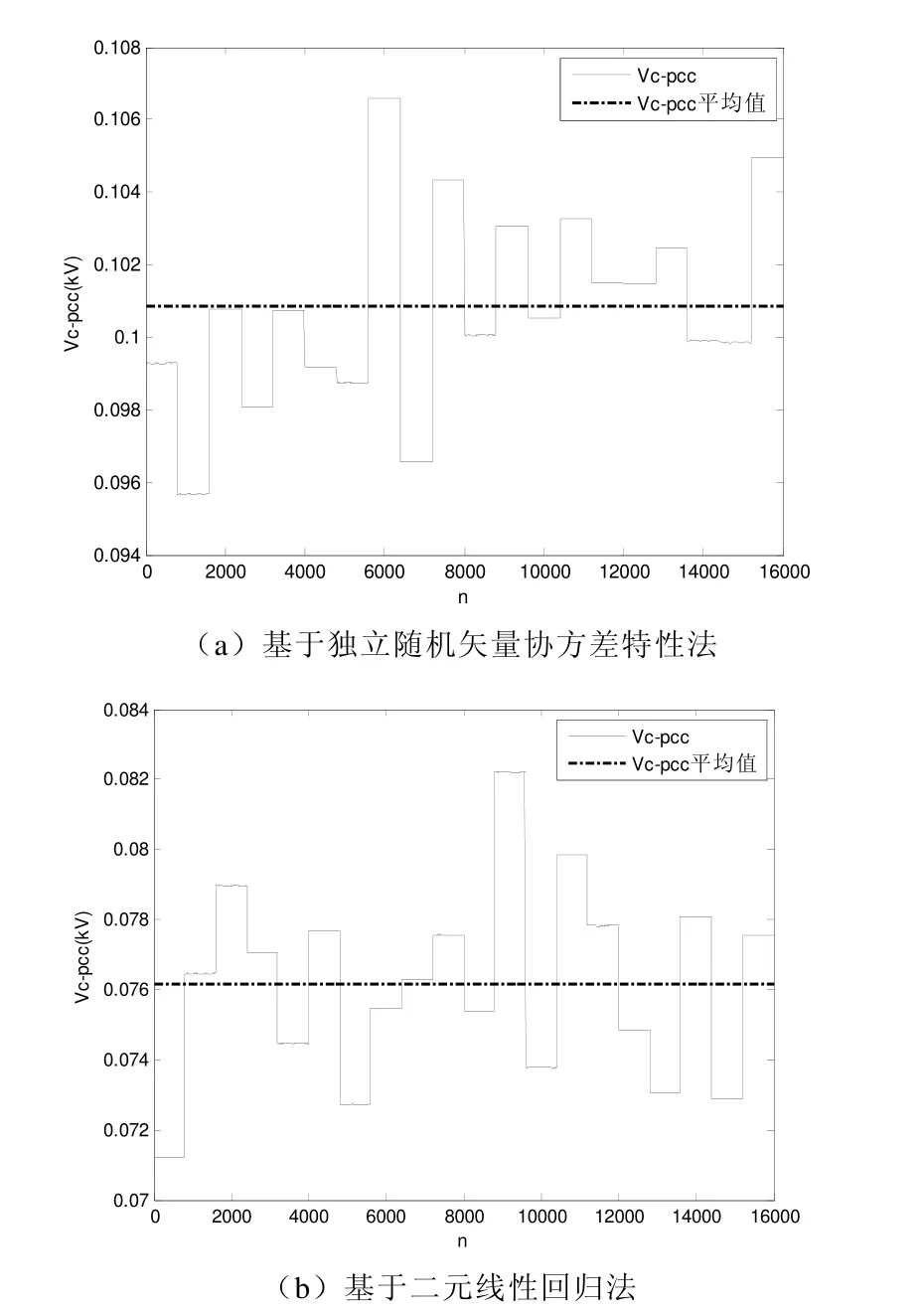
圖6 用戶側諧波電流在PCC 引起的電壓降 Vc-pcc
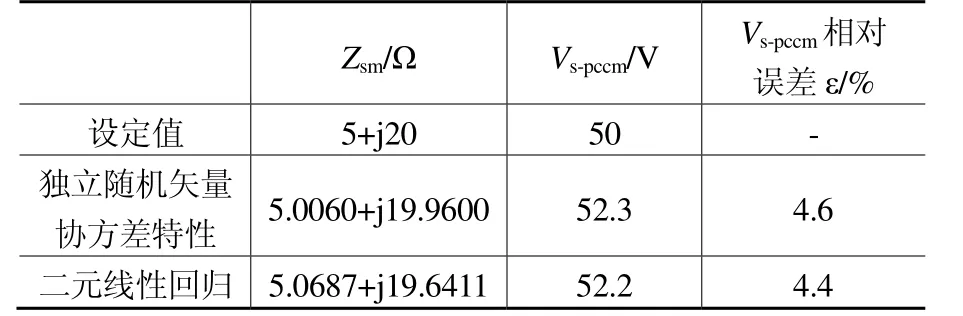
表1 原理模型中三次諧波計算分析結果比較
2.2 三電壓等級模型仿真分析
參照某實際變電站接線,利用PSCAD 搭建三電壓等級、整流負荷模型簡化電路如圖7所示。
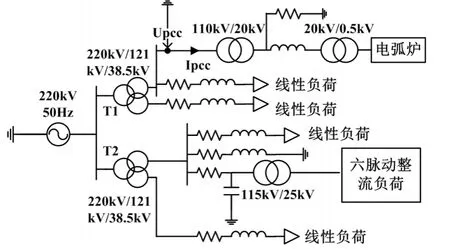
圖7 三電壓等級、整流負荷仿真模型簡化電路圖
該模型包括 220kV、110kV 和 35kV 三個電壓等級,相關參數如圖7所示。變壓器T1 110kV 母線作為PCC,采集其電壓和電流,用戶側連接的負荷包括電弧爐。電弧爐在煉鋼過程中表現出的強烈隨機性和時變性,會引發電力系統諸多電能質量問題,它產生的諧波對電網影響最大[15]。變壓器T2 110kV母線上連接6 脈動整流負荷。其它負荷均為線性負荷,有功功率為10MW,無功功率為8Mvar。
數據采樣、處理方法同1.1。圖7模型中將系統側電源置零,用戶側電弧爐斷開,在用戶側連接一個三次諧波電壓源,測量PCC 三次諧波電壓和三次諧波電流,用諧波電壓除以諧波電流,計算出系統側三次諧波阻抗的實際值Zs= 0.1560 + j12.5040。
兩種方法計算系統諧波阻抗Zsm、背景諧波電壓Vs-pccm、用戶諧波發射水平Vc-pccm、用戶諧波發射水平占PCC 該次諧波電壓的比例Vc-pccmVpccm如表2所示。
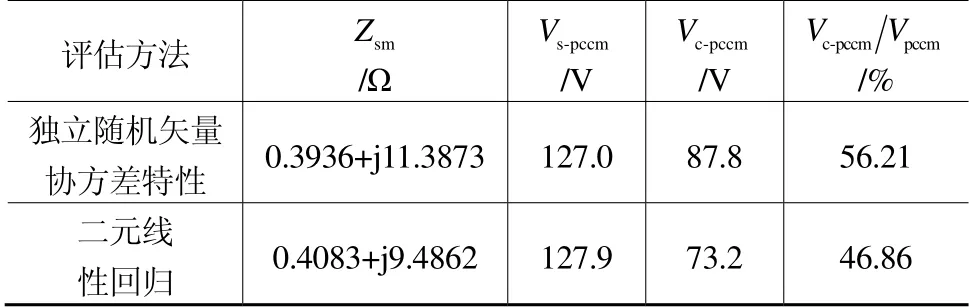
表2 三電壓等級模型中三次諧波計算結果比較
由表2看出兩種方法計算系統諧波阻抗、背景諧波電壓和用戶諧波發射水平的結果比較相近。“基于獨立隨機矢量協方差特性法”計算出系統諧波阻抗的幅值變化范圍為9.8~12.9Ω,“基于二元線性回歸法”為6.6~12.1Ω。相比之下,第一種方法計算出的諧波阻抗變化范圍較小。將計算出的系統諧波阻抗與實際的諧波阻抗Zs比較,發現第一種方法的計算值與實際值更為接近。
在三電壓等級模型中,諧波源除了電弧爐外還有一個六脈動整流負荷,六脈動整流負荷產生的諧波對于PCC 來說屬于系統側,因此用戶側諧波源的諧波發射水平占PCC 該次諧波電壓的比例較低。
2.3 IEEE 14 節點模型分析
在PSCAD 中對圖8所示的IEEE14 節點標準測試系統進行仿真計算。
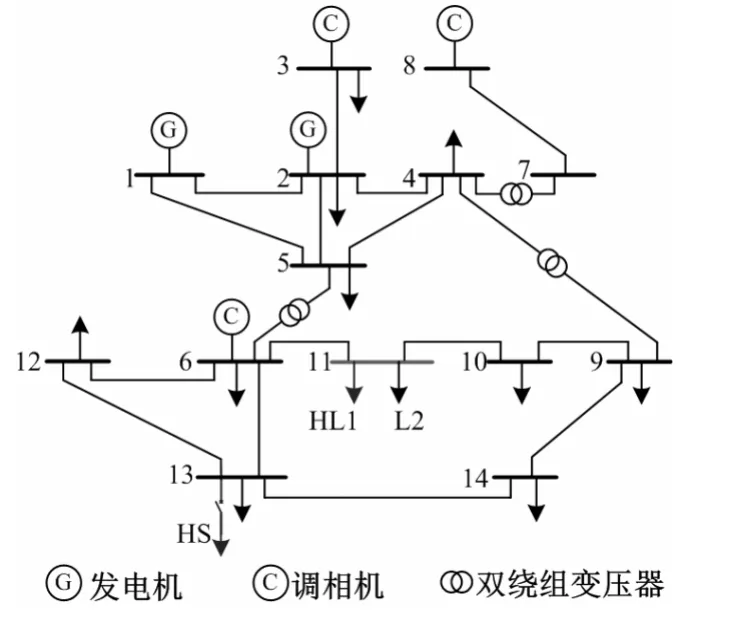
圖8 IEEE14 節點系統模型
該系統由兩臺發電機組、3 臺同步調相機、14條母線、15 條輸電線路和3 臺變壓器組成。計算中,將發電機和同步調相機等值為次暫態電抗,變壓器等值為阻抗,輸電線路以π 型等值電路表示[16],同時考慮長距離輸電線對地電容。
設定母線11 為PCC,HL1、L2 為母線處接入的兩個負荷,其中HL1 為負荷側諧波源;L2 為線性負荷。同時母線13 處接入諧波源負荷HS。將除去負荷 HL1、L2 的網絡其余部分視為該模型的系統側,仿真計算HL1 諧波源負荷在母線11 處產生的定量諧波責任。
1)單諧波源的IEEE 14 節點模型分析
斷開母線13 處的諧波源負荷HS,使整個系統僅含用戶側諧波源HL1。在單諧波源IEEE 14 節點模型中將系統側電源置零,用戶側諧波源HL1 斷開,在用戶側連接一個三次諧波電壓源,測量母線11 的三次諧波電壓和三次諧波電流。計算出系統側三次諧波阻抗實際值Zs= 0.0473 + j0.4082。
2)兩個諧波源的IEEE 14 節點模型分析
接入母線13 處的諧波源負荷HS,使系統側和用戶側均含諧波源,從而改變系統諧波。在兩個諧波源IEEE 14 節點仿真模型中將系統側電源置零,用戶側諧波源HL1 斷開,在用戶側連接一個三次諧波電壓源,測量公共連接點的三次諧波電壓和三次諧波電流。計算出系統側三次諧波阻抗的實際值Zs= 0.0486 + j0.4078。
兩種方法計算出單諧波源和兩個諧波源情況下系統諧波阻抗Zsm、背景諧波電壓Vs-pccm、用戶諧波發射水平Vc-pccm、用戶諧波發射水平占PCC 該次諧波電壓的比例Vc-pccmVpccm如表3所示。
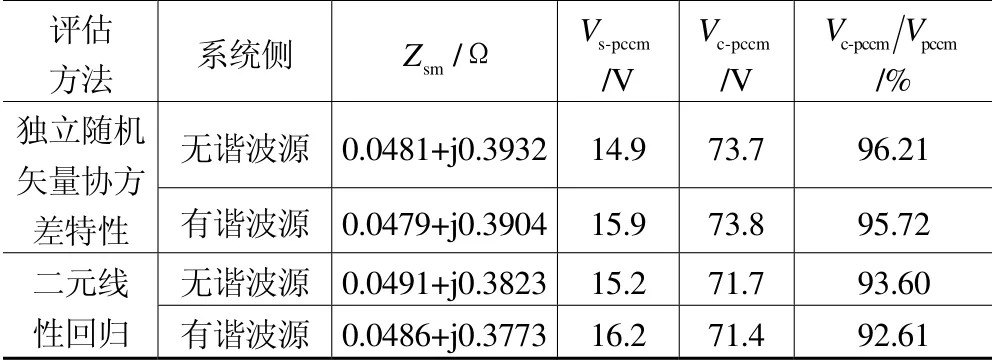
表3 IEEE 14 節點模型中三次諧波計算結果
從單諧波源IEEE 14 節點仿真結果看出“基于獨立隨機矢量協方差特性法”計算出系統諧波阻抗的幅值變化范圍為0.387~0.402Ω,“基于二元線性回歸法”為0.376~0.393Ω。相比之下,第一種方法計算出的諧波阻抗變化范圍較小,而且與實際系統諧波阻抗Zs更為接近。
從兩個波源的IEEE 14 節點仿真結果看出“基于獨立隨機矢量協方差特性法”計算出系統諧波阻抗的幅值變化范圍為0.386~0.397Ω,“基于二元線性回歸法”為0.369~0.389Ω。相比之下,還是第一種方法計算出的諧波阻抗變化范圍較小,并且與實際系統諧波阻抗Zs更為接近。
在IEEE 14 節點模型中,通過將系統側加入諧波源而其他結構不變來改變系統側諧波參數,對比兩種方法在系統側加入諧波源前后的各計算量,得出系統側諧波變化對整個網絡的影響情況。通過結果分析發現,兩種方法計算出的系統側諧波阻抗均要降低;系統側諧波電壓升高;用戶側諧波電壓基本保持不變;用戶諧波發射水平占PCC 諧波電壓的比例均比系統側未加入電弧爐的仿真結果低。
在系統模型中,若能進一步探究出如何逐項依次改變諧波相角、系統諧波阻抗以及諧波電壓的變化對估算結果的影響,必將可以更加細致地對兩種方法估算諧波發射水平的能力進行比較。
3 結論
本文通過大量仿真實驗對“基于獨立隨機矢量協方差特性”和“基于二元線性回歸”兩種諧波發射水平評估方法進行了對比研究,得出以下結論:
1)兩種方法在估算用戶諧波發射水平的計算中都具有很高的準確性,得出的結果具有一致性。
2)兩種方法的計算結果比較相近,但用獨立隨機矢量協方差特性的方法比用二元線性回歸法計算出的系統諧波阻抗幅值的波動范圍要小,穩定性較好,而且與實際值更為接近,而基于二元線性回歸法計算出的背景諧波電壓與實際設定值的相對誤差更小。
3)系統側增加諧波源后系統側諧波阻抗降低,系統側諧波電壓要增大,用戶側諧波電壓基本保持不變,用戶諧波發射水平占PCC 處諧波電壓的百分比降低。
[1] 肖湘寧,徐永海.電能質量問題剖析[J].電網技術,2000,24(3):36-38.
[2] Bollen M H J.Understanding power quality problems.Voltage sags and interruption[M].New York:IEEE PRESS,2000.
[3] 王安,粟時平,鄧奇峰,等.基于小波變換的暫態電能質量擾動檢測與定位研究[J].電氣技術,2012(4):21-25.
[4] 胡銘,等電能質量及其分析方法綜述[J].電網技術,2000,24(3):36-38.
[5] Wilsun Xu,YiLu Lin.A method for determining customer and utility harmonic contribution at the Point of common coupling[J].IEEE Transactions on Power Delivery,2000(15):804-811.
[6] 賈秀芳,華回春,曹東升,等.基于復線性最小二乘法的諧波責任定量劃分[J].中國電機工程學報,2013(4): 149-155,20.
[7] Yang H,Porotte P,Robert A.Assessing the harmonic emission level from one particular customer.Proceedings of PQA`94[A].Amsterdam: EPRI of USA[C].1994: B-2.08.
[8] Srinivasan.K.On separating customer and supply side harmonic contributions[J].IEEE Transactions on Power Delivery,1996,112(4): 1003-1012.
[9] 張安安,楊洪耕.基于畸變波形同步分層估計諧波阻抗的探討[J].電力系統自動化,2003(9):41-44.
[10] 趙勇,張濤,李建華,等.一種新的諧波源簡化模型[J].中國電機工程學報,2002(4):47-52.
[11] Wilsun Xu,Yilu Liu.A method for determining customer and utility harmonic contribution at the point of common coupling[J].IEEE Transactions on Power Delivery,2000,15(2):3-16.
[12] 趙勇,沈紅,李建華,等.諧波源的識別及其與非諧波源的分離方法[J].中國電機工程學報,2002(5):85-88.
[13] 惠錦,楊洪耕,林順富,等.基于獨立隨機矢量協方差特性的諧波發射水平評估方法[J].電力系統自動化,2009(7): 27-31.
[14] 張巍,楊洪耕.基于二元線性回歸的諧波發射水平估計方法[J].中國電機工程學報,2004(6):54-57.
[15] 張峰,何新,楊麗君.用于電能質量分析的電弧爐仿真模型[J].電氣技術,2013(7):34-38.
[16] Gursoy E,Niebur D.Harmonic load identification using complex independent component analysis[J].IEEE Transactions on Power Delivery,2009,24(1):285-292.

