基于雜草改進的模糊聚類雷達信號分選

王鶴朋，謝紅

哈爾濱工程大學信息與通信工程學院，黑龍江哈爾濱150001

在當前高密度復雜的電磁環(huán)境下，雷達信號分選是處理電子偵查信號的關(guān)鍵技術(shù)［1］，隨著雷達信號的交疊和輻射源數(shù)量的增加，對于未知參數(shù)的雷達信號［2］，傳統(tǒng)的分類方法，例如K均值算法是對數(shù)據(jù)的硬性劃分。后來有人提出FCM算法，F(xiàn)CM算法是對K均值聚類的一種改進，是對數(shù)據(jù)的柔性劃分。但是，對于這2種聚類算法受到初始聚類中心敏感、需要事先設定分類數(shù)目的限制，往往得不到理想的聚類效果，因此，如何準確地確定聚類數(shù)目是決定聚類有效性的關(guān)鍵，也是亟待解決的問題［3-5］。因此，本文提出一種雜草優(yōu)化模糊聚類算法，該算法在給定的范圍內(nèi)選擇初始聚類中心，根據(jù)不同數(shù)目的聚類中心進行并行聚類，自動篩選出最佳的聚類數(shù)目。

1 FCM算法

模糊K均值聚類算法(Fuzzy C-Means clustering，F(xiàn)CM)是1974年由Bezdek提出的，屬于利用隸屬度判別樣本點屬于某一類程度進行的聚類技術(shù)［6-7］，是對傳統(tǒng)的K均值算法的一種改進。

模糊聚類算法的基本思想:首先，在數(shù)據(jù)樣本中，隨機地選擇 C 個對象 u1，u2，…，uc，每個樣本點相對于整個數(shù)據(jù)的隸屬度和為1，即

式中:p(wi|xj)為第j個樣本點相對于第i個聚類中心的隸屬度，取值在［0，1］之間。

FCM的目標函數(shù)的一般形式為:

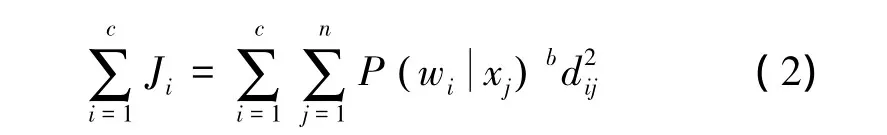
式中:dij=‖xj－ui‖2;b(b＞1)為模糊系數(shù)，決定聚類的模糊程度。

對于不同的隸屬度有不同的目標函數(shù)值，模糊K均值聚類的核心思想就是求出使得目標函數(shù)取得最小值的隸屬度矩陣，目標函數(shù)對求偏導數(shù)，令其為0，得到

重新計算P (wi|xj)和ui，對該運算過程進行更新迭代，直至得到目標函數(shù)值足夠小時完成運算。

2 雜草優(yōu)化的模糊聚類算法

擴張性雜草進化算法(invasive weeds optimization，IWO)是2006年 Mehrabian 等［8］基于自然界雜草進化原理提出的一種智能算法，具有結(jié)構(gòu)簡單、魯棒性好的特點，能夠有效防止搜索過程中陷入局部最優(yōu)。

2.1 初始化群體

實驗表明選擇合理的聚類數(shù)目和聚類中心是決定聚類效果的關(guān)鍵，采用IWO來自動選取FCM算法的初始聚類中心，設數(shù)據(jù)集總數(shù)為N，由于聚類數(shù)目未知，不妨設聚類數(shù)目為 Ci，其中 Ci∈(Cmin，Cmax)，一般 Ci=2，Cmax=。利用雜草算法不斷產(chǎn)生新的種子［9-10］，直到雜草數(shù)最大，在整個數(shù)據(jù)集內(nèi)搜索最好的聚類數(shù)目和聚類中心，使得適應值達到最大。

2.2 適應度函數(shù)

聚類有效性的評價(適應度函數(shù))采用silhouette準則，首先給出2個定義:

類內(nèi)距離:指同一個類中2個樣本點之間的距離，表達式為

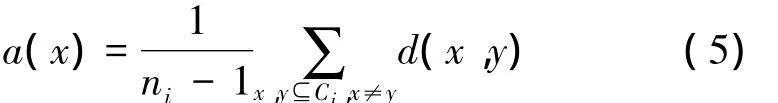
類間距離:指2個不同類中的2個樣本點之間的距離，表達式為

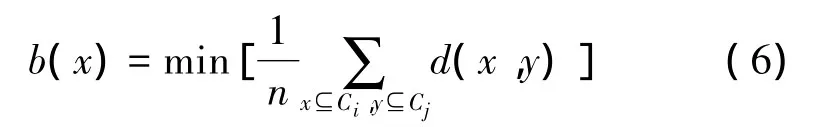
silhouette準則的基本思想是通過計算類內(nèi)距離和類間距離來評價聚類的質(zhì)量，該值越大，表示聚類的結(jié)果越好，表達式為

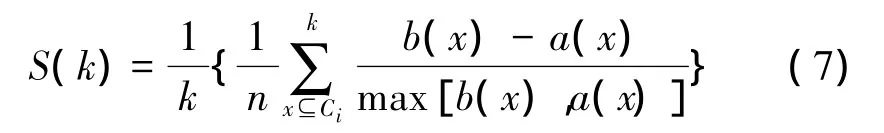
式中:k為聚類數(shù)目，ni為第i類樣本中的樣本總數(shù)。

3 基于IWO-FCM的雷達分選

針對較為復雜的輻射源信號，本文利用到達角(DOA)、脈寬(PW)、載頻(RF)這3個參數(shù)聯(lián)合描述雷達輻射源信號的特征。

3.1 基于雜草優(yōu)化模糊聚類的雷達分選的基本流程

IWO-FCM基本流程如圖1。

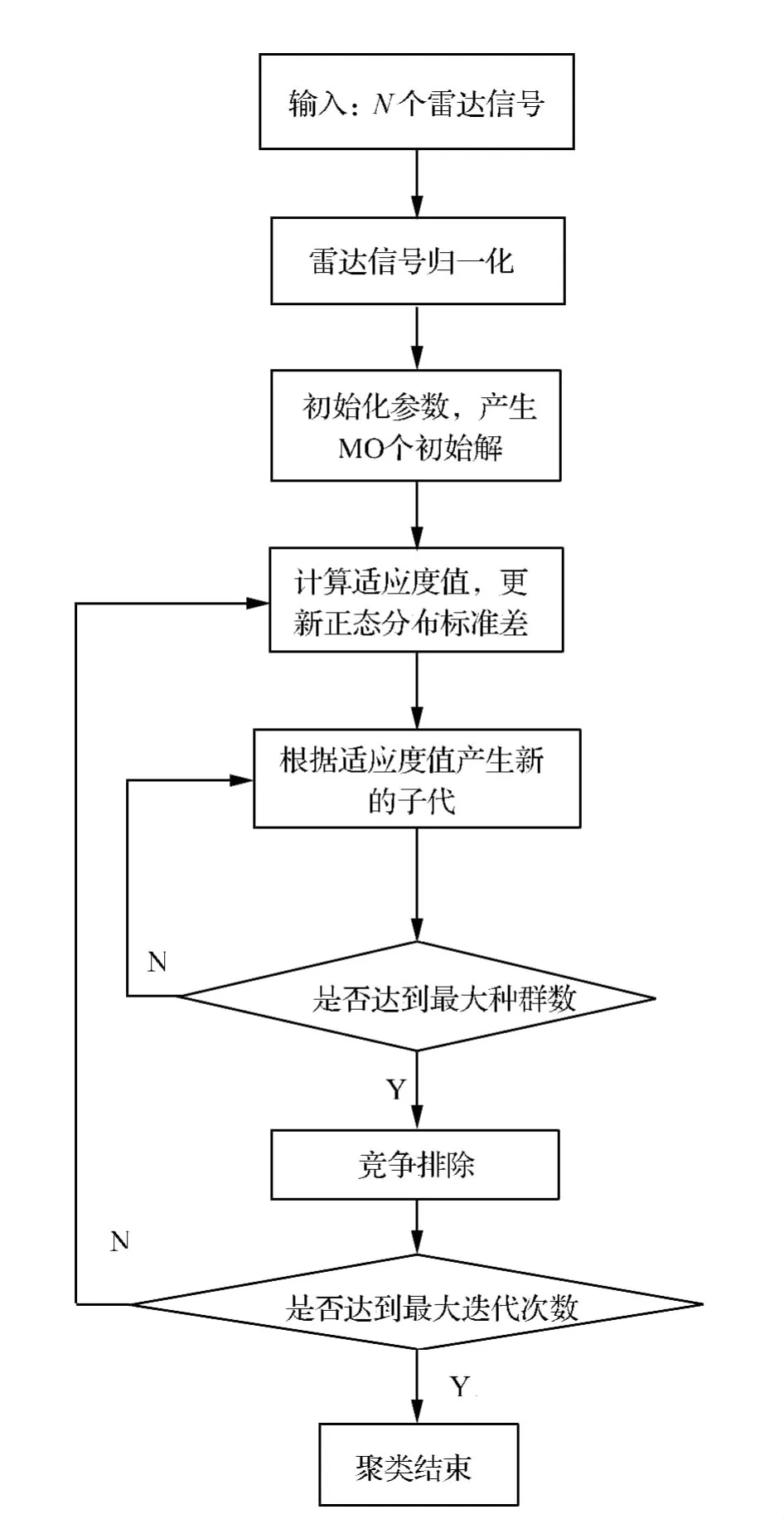
圖1IWO-FCM算法流程圖

1)標準化雷達數(shù)據(jù)樣本。對N個三維的樣本數(shù)據(jù) xi=(xi1，xi2，xi3)，i=1，2，…，n，先求出雷達信號每一維數(shù)據(jù)樣本的平均值和標準差C，其中

由此，雷達數(shù)據(jù)樣本的標準化值為

2)初始化群體參數(shù)，在設置的搜索空間內(nèi)產(chǎn)生M0個初始解。

3)計算適應度的值，更新正態(tài)分布的標準差。

4)按照適應度的值產(chǎn)生新的子代，適應度值大的產(chǎn)生子代多，適應度值小的產(chǎn)生子代少，直到子代數(shù)目達到設置的最大種群規(guī)模。

5)競爭排除，將父代和子代產(chǎn)生的適應度值放在一起排列，排除適應度值小的樣本點。

6)判斷是否達到最大的迭代次數(shù)，若是，則輸出最優(yōu)值;若否，返回步驟3)。

3.2 實驗結(jié)果及分析

實驗采用Matlab R2010a軟件進行仿真，在Intel(R)Celeron(R)CPU 2.60 GHz，2 GB 內(nèi)存，Windows Xp系統(tǒng)的計算機上運行。本文模擬4部雷達信號脈沖進行實驗來驗證算法分選的準確性，信號的參數(shù)如表1，三維顯示如圖2。

為了進行對比，使用相同的雷達信號數(shù)據(jù)集，分別采用K均值聚類，AP聚類以及改進的模糊聚類進行仿真分析，得到分選結(jié)果。首先，采用K均值聚類算法對上述的4類雷達進行聚類，將K的值設為4，默認為已經(jīng)知道聚類數(shù)目，Matlab仿真效果如圖3。

從表2中可以看出，對于重疊比較嚴重的信號，采用K均值聚類算法的聚類結(jié)果不理想，漏選和錯選的現(xiàn)象比較嚴重。下面對雷達信號采用AP聚類算法進行分選，圖4為分選的效果圖。

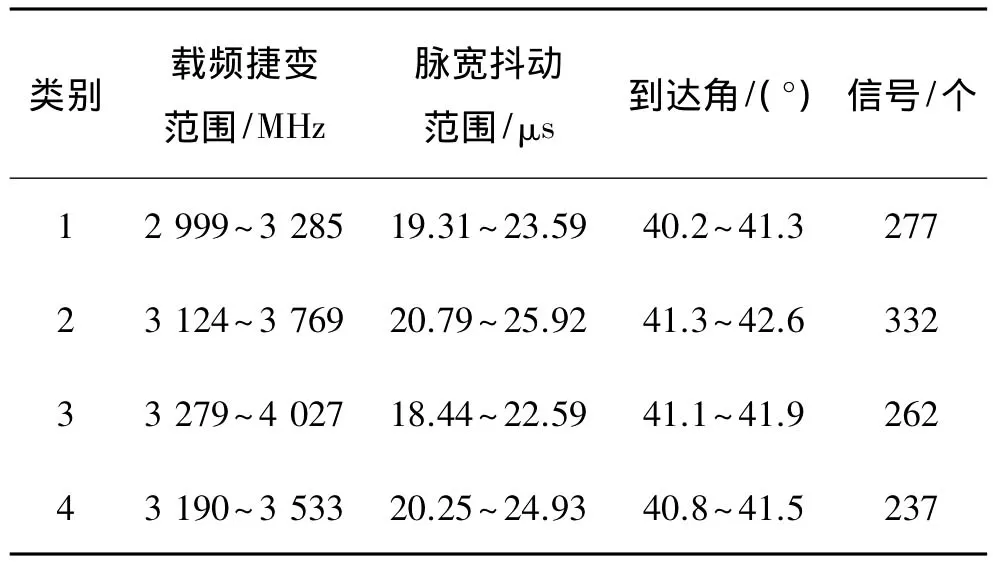
表1 雷達輻射源數(shù)據(jù)表

圖2 聚類前的雷達輻射源信號

圖3 基于K-means的雷達信號分選

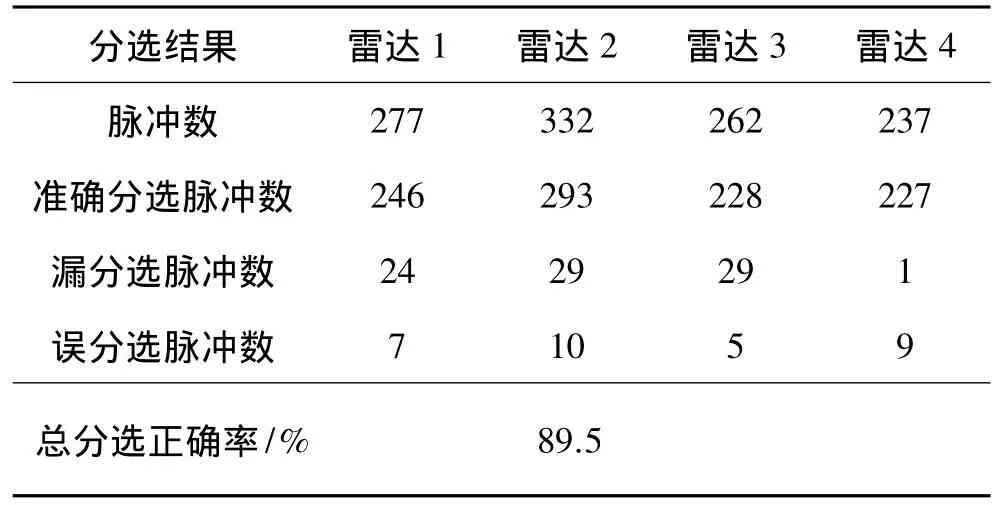
表2 基于K-means的分選結(jié)果

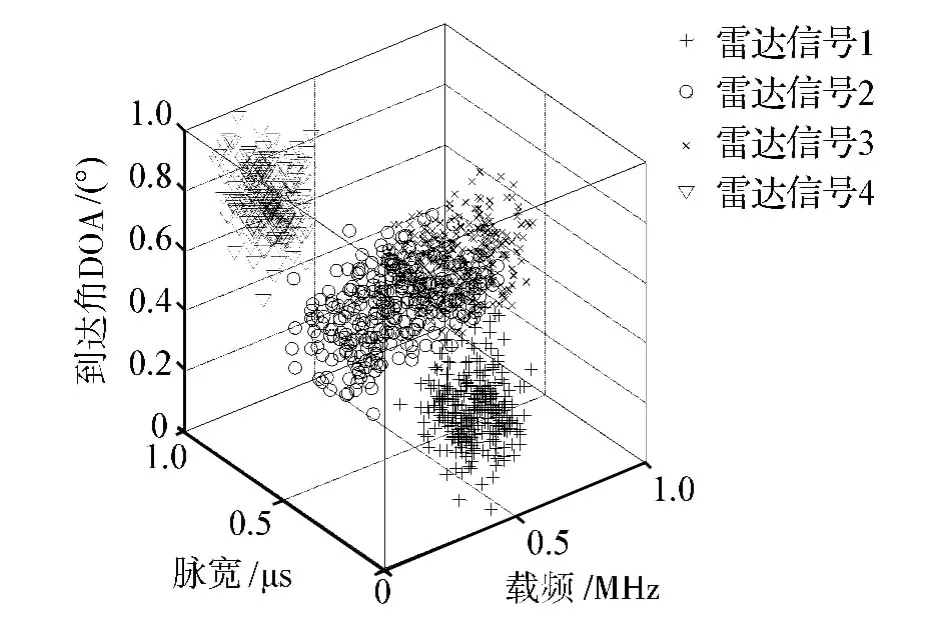
圖4 基于AP聚類的雷達信號分選

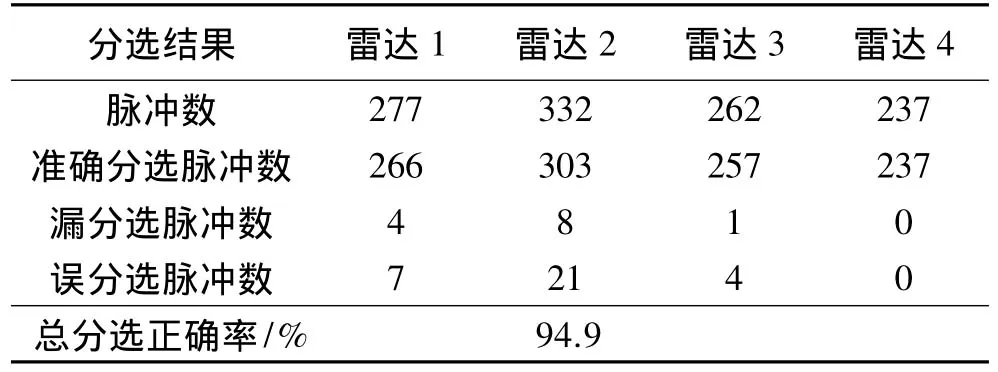
表3 基于AP聚類的分選結(jié)果

從表3中可以看出AP聚類算法不但不需要設定初始聚類數(shù)目，并且聚類效果比K均值要好，但是以上2種聚類仍然不能達到較高的分選正確率，因此，下面采用雜草改進的模糊聚類算法，如圖5。

圖5 基于IWO-FCM的雷達信號分選

表4 基于IWO-FCM的分選結(jié)果

由上表分析可以發(fā)現(xiàn)，基于雜草優(yōu)化的模糊聚類將雷達輻射源信號準確地分為了4類，由于雷達1和雷達2載頻比較接近，雷達2和雷達3的脈寬交疊比較嚴重，在分選時出現(xiàn)幾個錯誤，雷達4分選全部正確，總分選正確率達到97.4%。

3種聚類算法分選的正確率比較如表5所示。

表5 3種算法聚類結(jié)果對比

根據(jù)以上實驗對比可以看出，相對于傳統(tǒng)的聚類算法，基于雜草改進的模糊聚類算法不僅對交疊較輕的雷達信號達到100%分選正確率，并且對交疊現(xiàn)象比較嚴重的雷達信號具有比較理想的聚類效果。

4 結(jié)束語

本文介紹了雜草優(yōu)化的模糊聚類算法在雷達分選上的應用，對于未知的雷達信號，如何準確地確定聚類數(shù)目是決定聚類有效性的關(guān)鍵，通過Matlab仿真分析，該算法克服了未知雷達信號的聚類數(shù)目分選準確率不高的問題，能夠根據(jù)雷達信號的聯(lián)合參數(shù)完成信號分選的任務，與傳統(tǒng)的聚類算法相比，保持了較高的分選精度。

［1］趙國慶.雷達對抗原理［M］.西安:西安電子科技大學出版社，1999:1-7.

［2］劉旭波，司錫才.基于改進的模糊聚類的雷達信號分選［J］.彈箭與制導學報，2009，29(5):278-282.

［3］孫鑫，侯慧群，楊承志.基于改進K-均值算法的未知雷達信號分選［J］.現(xiàn)代電子技術(shù)，2010，17:91-96.

［4］向嫻，湯建龍.一種基于網(wǎng)格密度聚類的雷達信號分選［J］.火控雷達技術(shù)，2010，39(4):67-72.

［5］賀宏洲，景占榮，徐振華.雷達信號的模糊聚類分選方法［J］.航空計算技術(shù)，2008，38(5):21-24.

［6］ABDEL K R.Genetically improved PSO algorithm for efficient data clustering［C］//2010 Second International Conference on Machine Learning and Computing(ICMLC)，Port Said，Egypt，2010:71-75.

［7］BALAFAR M A，RAMLI A R，MASHOHOR S et al.Compare different spatial based fuzzy-C mean(FCM)extensions for MRI image segmentation［C］//2010 2ndInternational Conference on Computer and Automation Engineering(ICCAE).Azerbaijan，Iran，2010:609-611.

［8］陳歡.入侵雜草優(yōu)化算法的改進分析及應用研究［D］.南寧:廣西民族大學，2013:4-5.

［9］楊善林，李永森，胡笑旋，等.K-means算法中的 k值優(yōu)化問題研究［J］.系統(tǒng)工程理論與實踐，2006(2):97-101.

［10］于劍，程乾生.模糊聚類方法中的最佳聚類數(shù)的搜索范圍［J］.中國科學:E 輯，2002，32(2):274-276.