BMH2C單模匹配算法的研究與改進
王艷霞,江艷霞,王亞剛,李 燁
BMH2C單模匹配算法的研究與改進
王艷霞,江艷霞,王亞剛,李 燁
(上海理工大學光電信息與計算機工程學院,上海 200082)
BMH2C算法綜合BMH和BMHS算法,利用當前窗口字符[]及其下一字符[+1]組成的雙字符串來決定模式串右移量,具有比BM算法、BMH算法、BMHS算法更優的性能。但對于雙字符串在模式串中出現一次及以上的情況,BMH2C算法中的模式串右移量仍有待進一步增大,從而減少當前窗口右移次數,提高BMH2C算法的匹配效率。為此,在BMH2C算法的基礎上提出一種改進算法,該算法考慮雙字符串[][+1]在模式串中出現的次數,以及該雙字符串在模式串中對應位置的后繼字符與字符[+2]的相等關系。改進算法利用2個右移數組和1個模式串預處理數組,在匹配過程中通過判斷字符[+2]與模式串預處理數組中相應字符是否相等,從而選擇2個右移數組之一的對應值作為當前窗口的右移量。實驗結果顯示,在相同條件下,對于當前窗口移動次數和匹配所耗時間,BMH2C改進算法比BMH2C算法分別平均減少11.33%和9.40%,有效提高了匹配效率。
模式匹配;BMH2C算法;字符串;右移;預處理
1 概述
模式匹配是指在文本串=[0,1,…,-1]中找到一個模式串=[0,1,…,-1](≥),即模式串是文本串的子串[1]。模式匹配有單模匹配和多模匹配2種[2],經典的單模匹配算法有KMP算法[3]、BM算法[4]。KMP算法的字符比較是從左到右進行的,且模式串右移量一般較小,而BM算法采用了從右到左的匹配,其右移量由壞字符規則和好后綴規則共同決定,最大值可達到模式串的長度,因而BM算法比KMP算法更優,得到了極為廣泛的應用[5]。與此同時,BM算法的各種改進算法也層出不窮,如BMH算法、BMHS算法、BMH2C算法等。這3種算法都只采用了壞字符規則,不同的是BMH算法利用當前窗口字符決定模式串右移量,BMHS算法利用當前窗口下一個字符決定右移量,而BMH2C算法利用當前窗口字符及其下一個字符組成的雙字符串決定右移量。它們簡化了預處理階段的時間開銷[6],匹配效率比BM算法高。而且BMH2C算法利用了雙字符串在模式串中出現的概率比單個字符小的特點,匹配性能較前幾者更佳。但是對于雙字符串在模式串中出現一次及以上的情況,BMH2C算法無法做到每次獲得最大右移量,匹配過程中當前窗口移動次數有待進一步降低以提高匹配效率。
針對上述BMH2C算法存在的缺陷,本文提出一種改進算法I_BMH2C。考慮到當前窗口雙字符串[][+1]在模式串中出現的次數,以及雙字符串的后繼字符[+2]與該雙字符串在模式串中的后繼字符是否相等,I_BMH2C在BMH2C算法的基礎上分別新增一個模式串右移數組和一個模式串預處理數組。匹配過程中通過判斷字符[+2]與模式串預處理數組中相應字符是否相等,從而選擇右移數組。
2 BM算法及其相關算法
2.1 BM算法
BM算法的三大特點是采用了從右至左的掃描方式、壞字符規則以及好后綴規則。首先文本串[0,1,…,-1]的最左端與模式串[0,1,…,-1](為文本串的長度,為模式串的長度,≥)的最左端對齊,然后在當前窗口字符[]處從右至左掃描,依次比較[]和[-1],[-1]和[-2],…,[-+1]和[0]。若發現某處不匹配,則根據預處理好的數組和數組,將模式串向右移動兩者中較大者的距離,依次重復上述步驟,直到匹配成功或是文本串中的字符全部比較完。
2.1.1 壞字符規則
數組的定義分2種情況:字符不在模式串中。字符在模式串中,設為在模式串中最右位置處的下標。
數組的定義如下:
在從右至左的掃描過程中,若文本串中某個字符[-](0≤<)與模式串中的字符[--1]不相等,則稱[-]為壞字符,根據預先處理好的數組將模式串向右移動[[-]]個字符。
2.1.2 好后綴規則
數組計算公式如下:
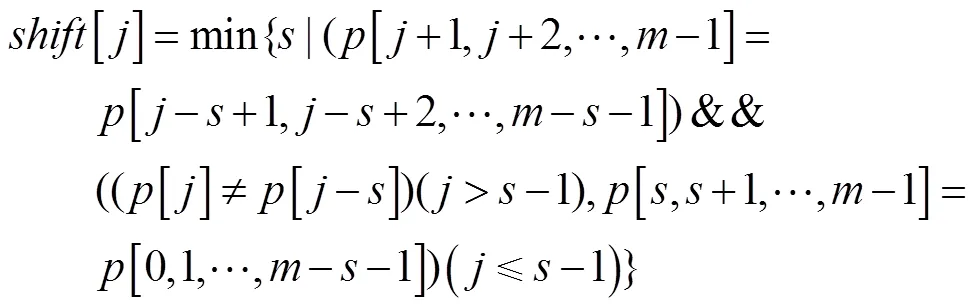
假設匹配進行到比較文本串字符[-+1,-+2,…,]和模式串字符[0,1,…,-1],從右至左的掃描過程中,發現[-++1]與[]失配的同時,已有[-++2,-++3,…,]與[+1,+2,…,-1]匹配成功,則稱[-++ 2,-++3,…,]為好后綴。此時模式串根據預先計算好的[]值向右移動相應的距離。
關于壞字符規則和好后綴規則,文獻[7]研究表明:BM算法中模式串的右移量在絕大多數情況下取決于壞字符規則,且壞字符規則較好后綴規則簡單易于實現。
2.2 BMH算法及BMHS算法
文獻[8]提出了一種改進的BM算法——BMH算法。該算法只使用了壞字符規則。在匹配過程中若發現某處不匹配,則根據當前窗口字符[]來啟發模式串的右移量。令[]=,則具體的移動公式如下:
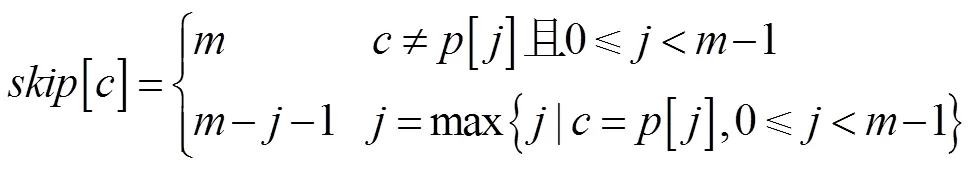
由于數組的預處理比數組的預處理要簡單得多,而且BMH算法省去了兩者比較大小這一步驟,因此在實際匹配過程中BMH算法效率要高于BM算法。
在BMH算法的基礎上,文獻[9]提出了BMHS算法,該算法與BMH算法的思想基本一致[10-11],不同之處在于BMHS算法是利用當前窗口的下一個字符[+1]來啟發模式串的右移量。
2.3 BMH2C算法
模式匹配算法效率的高低主要取決于模式串向右移動的次數,即當前窗口向右移動的次數。當失配發生時,若模式串每次移動盡可能大的距離,顯然減少了當前窗口總的移動次數,可以有效地提高匹配效率。因此,文獻[12]在BMH和BMHS算法的基礎上提出了一種新的改進算 法——BMH2C算法。該算法的基本思想也是基于壞字符規則,與BMH、BMHS算法的不同之處在于利用了當前窗口字符[]及其下一個字符[+1]所組成的雙字符串[][+1]來啟發當前窗口的右移距離:若雙字符串[][+1]不在模式串中,且[+1]與[0]不相等,則模式串右移+1;若字符串[][+1]不在模式串中,但[+1]與[0]相等,則模式串右移;若[][+1]出現在模式串[][+1](0≤≤-2)處,則右移模式串使得兩者對齊。
BMH2C算法的預處理部分可以用一個二維數組來表示,設字符集為ASCII碼,大小從0到255,則數組預處理算法如下:
//將字符集中任意2個字符組成的字符串的skip值初始化為//m+1
for i=0 to 255{
for j=0 to 255{
skip[i][j]=m+1; j++;
}
i++;
}
//若任意2個字符組成的字符串的后一個字符與p[0]相等,則//重新賦值為m
for i=0 to 255{
skip[i][p[0]]=m; i++;
}
//模式串中的字符串根據其位置來確定skip值
for i=0 to m-1{
skip[p[i]][p[i+1]]=m-i-1; i++;
}
從右向左掃描的過程中,若遇到壞字符,則模式串向右移動[[]][[+1]]個字符。下面用一個實例來說明BMH2C算法的匹配過程,如圖1所示:文本串=“decbedade abaccdcdeadbad”,模式串=“adbad”。由圖可以看出,當前窗口一共向右移動了6次。

圖1 BMH2C算法的匹配過程
設字符集中每個字符在模式串中出現的概率為(0<< 1),則2個字符同時出現在模式串中的概率為2。顯然,雙字符串出現在模式串中的概率遠低于單個字符出現在模式串中的概率,在實際匹配過程中,BMH2C算法的平均移動量較BMH和BMHS算法都大,有效減少了模式串向右移動的次數,匹配效果更好。
3 改進的BMH2C算法
3.1 I_BMH2C算法設計思路
為了進一步提高BMH2C算法的效率,本文提出了I_ BMH2C算法。通過觀察文本串和模式串可知:一部分雙字符串不會在模式串中出現,另一部分雙字符串僅在模式串中出現一次,還有較少一部分雙字符串可出現2次或2次以上。此時需分3種情況討論:
(1)當[][+1]在模式串中出現0次時,模式串右移,直接跳過該雙字符串。
(2)當[][+1]在模式串中出現1次時,設在[][+1] (0≤≤-3)處:若雙字符串[][+1]的后一個字符[+2]與雙字符串[][+1]的后一個字符[+2]不相等,則模式串右移,直接跳過[][+1];若[+2]=[+2],則模式串右移--1個字符。另外還有一種特殊情況需單獨考慮:當[][+1]出現在模式串[-2][-1]處時,由于[-1]后面沒有字符,此時模式串向右移動一個字符。
(3)當[][+1]在模式串中出現2次或2次以上,模式串按從右向左統計,設第1次出現在[][+1](1≤≤-2)處,第2次出現在[][+1](0≤<)處:若[+2]≠[+2],則模式串右移--1個字符,否則右移--1個字符。
該算法的具體設計思路為:在BMH2C算法原有右移數組1的基礎上新增一個模式串右移數組2,在匹配過程中若發現某處失配,則判斷[][+1]的后一個字符[+2]和[][+1]的后一個字符[+2]是否相等,若不等則將模式串向右移動2[[]][[+1]]個字符,否則移動1 [[]][[+1]]個字符。其中,2數組的設計思想是:首先初始化2數組,方法同1數組;然后按模式串從右至左統計各雙字符串[][+1](0≤<-1)在模式串中出現的次數,當統計值為2時,假設此時統計進行到[][+1] (0≤<-2),則將2[[]][[+1]]重新賦值為--1;此外還需單獨考慮上述(2)中的一種特殊情況,由于[-1]后面沒有字符,2[[-2]][[-1]]=1。由1和2數組的對比可知,2數組的值大于或等于1的對應值,因此,該算法可使得模式串每次向右移動盡可能大的距離,從而提高匹配效率。
3.2 I_BMH2C算法的預處理
預處理階段需用到2個跳躍數組1和2。1的計算方法和BMH2C算法中的一樣,此處主要講解2的求解方法。
//將字符集中任意2個字符組成的字符串的skip2值初始化為//m+1
for i=0 to 255{
for j=0 to 255{
skip2[i][j]=m+1;j++;
}
i++;
}
//若任意2個字符組成的字符串的后一個字符與p[0]相等,則//重新賦值為m
for i=0 to 255{
skip2[i][p[0]]=m; i++;
}
//從右至左統計模式串中雙字符串p[i]p[i+1]出現的次數
for i=m-2 to 0{
統計次數
//當統計到某個雙字符串出現第2次時計算出對應的右移 //量,計算方法與BMH2C算法一樣
if(字符串p[i]p[i+1]出現的次數==2)
Then skip2[p[i]][p[i+1]]=m-i-1;
endif
i––;
}
//當t[k]t[k+1]出現在p[m-2][m-1]處時,模式串向右移動一//個字符
skip2[p[m-2]][p[m-1]]=1;
由于在匹配過程中要判斷[+2]與[+2]是否相等,預處理階段還涉及到一個數組[][]。假設[][+1]出現在模式串[][+1]處,則[[]][[+1]]存放的是字符[+2],而+2又可用-1[[]][[+1]]+1表示,因此[[]][[+1]]=[-1[[]][[+1]]+1]。
//prep數組的預處理
for i=0 to 255{
for j=0 to 255{
prep[i][j]=p[m-skip1[i][j]+1]; j++;
}
i++;
}
3.3 I_BMH2C算法匹配過程
假設匹配進行到比較[0,1,…,-1]和[-+1,-+2,…,],從右至左比較[]和[-1],[-1]和[-2],[-2]和[-3],…,若發現某處失配,則判斷[[]] [[+1]]與[+2]是否相等,此時分2種情況討論:
(1)若不相等,則模式串右移2[[]][[+1]]。
(2)若相等,則模式串右移1[[]][[+1]]。
以上2種情況已包含了雙字符串[][+1]不在模式串中的情況,所以不必單獨考慮。匹配算法偽代碼描述如下:
for k=m-1 to n-1
{//文本串與模式串的最左端對齊,t[k]為當前窗口字符
i=k; j=m-1;
While(t[i]==p[j])//從右至左依次掃描,若某處失配則跳出循環
i––; j––;
EndWhile
If(j==-1)
Then return(i+1);
//匹配成功,返回模式串在文本串中出現的指針
Endif
If(prep[t[k]][t[k+1]]!=t[k+2])
Then k=k+skip2[t[k]][t[k+1]];//采用改進的I_BMH2C算法//將當前窗口右移skip2[t[k]][t[k+1]]
Else Then k=k+skip1[t[k]][t[k+1]];
Endif
}
下面用實例來具體說明I_BMH2C算法的匹配過程,如圖2所示。
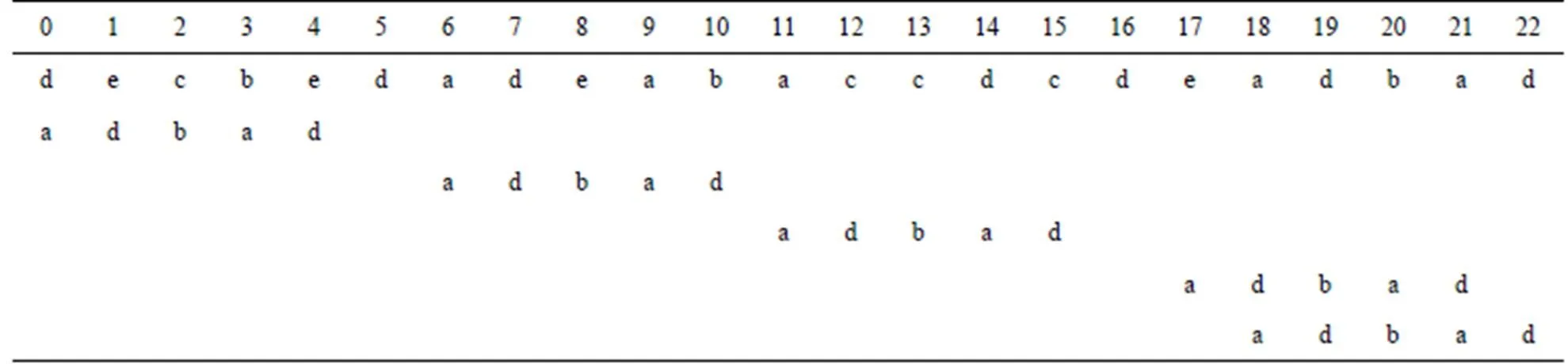
圖2 I_BMH2C匹配過程
第1輪匹配時,當前窗口的指針=4,雙字符串[4][5]不在模式串中,模式串右移1[[4]][[5]]=2[[4]] [[5]]=5+1=6個字符;第2輪匹配時,當前窗口的指針= 4+6=10,雙字符串[10][11]在模式串[2][3]處出現1次,由于[4]≠[12],模式串右移2[[10]][[11]]=5個字符;第3輪匹配時,當前窗口的指針=10+5=15,雙字符串[15][16]不在模式串中,模式串右移1[[15]][[16]]=2 [[15]][[16]]=6;第4輪匹配時,當前窗口的指針=15+6=21,雙字符串[21][22]在模式串[3][4]處出現1次,模式串右移1[[21]][[22]]=1個字符;第5輪匹配成功。整個過程模式串右移了5次。
4 實驗結果
從理論上來講,I_BMH2C算法產生最大右移量的概率比BM、BMH、BMHS、BMH2C算法都高,當前窗口移動次數會相應減少,匹配效果更優。
本文實驗是在虛擬機上進行的,實驗環境為:物理機系統Microsoft Windows XP SP3,配置為Intel CPU 2.66 GHz,內存3.25 GB;虛擬機為VMware Workstation 9,系統Ubuntu11.10,配置為內存1 GB,硬盤50 GB,編譯器為 gcc 4.6.1。
實驗1采用的是一段純英文文本,大小為20.5 MB,通過BM、BMH、BMHS、BMH2C、I_BMH2C這5種算法對不同長度模式串分別進行匹配,統計匹配過程中窗口右移次數;實驗2是對大小為55.1 MB的純英文文本統計各種算法匹配用時。
實驗1測試5種算法的窗口右移次數,結果如表1 所示。
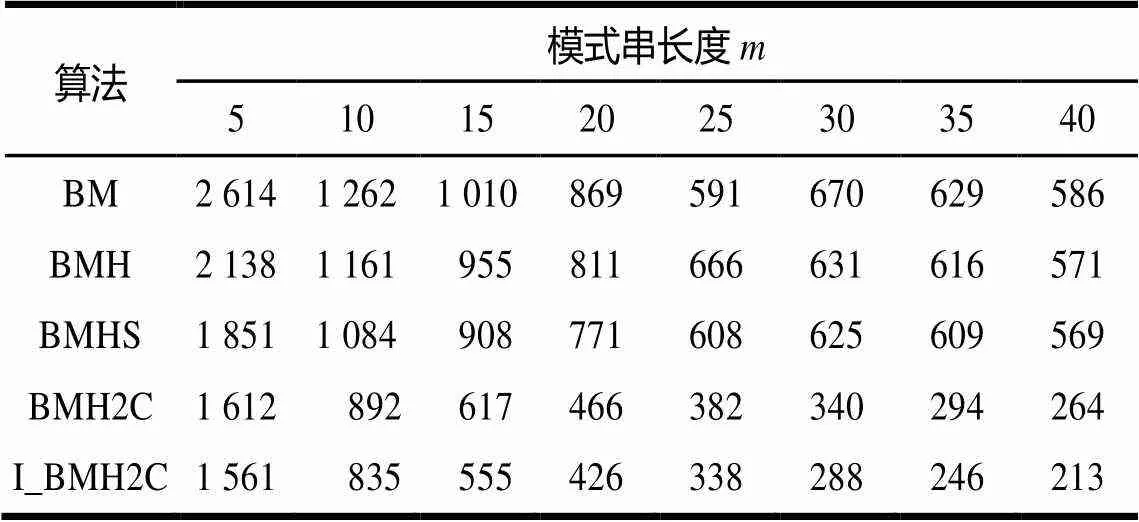
表1 窗口右移次數
實驗2測試各種算法匹配用時,結果如表2所示。

表2 匹配消耗時間 ms
由實驗1和實驗2可以看出,在模式串一定的情況下,采用I_BMH2C算法所需的窗口移動次數和匹配所耗時間比BM、BMH、BMHS、BMH2C算法均小,且由計算可得:I_BMH2C算法的當前窗口移動次數比BMH2C的平均少11.33%;I_BMH2C算法的匹配所耗時間比BMH2C的平均少9.40%。因此,本文對BMH2C的改進算法I_BMH2C有效地減少了模式匹配過程中窗口右移次數,也減少了匹配所耗時間,提高了匹配效率。
5 結束語
模式匹配效率的高低直接影響到計算機系統性能的好壞。本文介紹了經典的BM算法及其改進算法BMH和BMHS算法,重點介紹了BMH2C算法,并在該算法的基礎上提出了一種改進的I_BMH2C算法,I_BMH2C算法有效提高了產生最大右移量的概率,使得匹配過程中窗口移動次數減小,匹配速度更快,較BM、BMH、BMHS、BMH2C算法更優。
[1] 錢 穎, 劉國華, 陳子陽, 等. 模式匹配技術[J]. 燕山大學學報, 2006, 30(4): 340-344.
[2] 張 娜, 張 劍. 一個快速的字符串模式匹配改進算法[J].微電子學與計算機, 2007, 24(4): 102-105.
[3] 楊戰海. KMP模式匹配算法的研究與分析[J]. 計算機與數字工程, 2010, 38(5): 38-41.
[4] Boyer R S, Moore J S. A Fast String Searching Algorithm[J]. Communications of the ACM, 1977, 20(10): 762-722.
[5] 揣錦華, 鄭 景, 關 銳. BM模式匹配算法的研究和改 進[J]. 電子設計工程, 2012, 20(19): 52-54.
[6] 單懿慧, 蔣玉明, 田詩源. 面向入侵檢測的改進BMHS模式匹配算法[J]. 計算機工程, 2009, 35(24): 170-173.
[7] 劉勝飛, 張云泉. 一種改進的BMH模式匹配算法[J]. 計算機科學, 2008, 25(11): 164-166.
[8] Horspool R N. Practical Fast Searching in Strings[J]. Software Practice and Experience, 1980, 10(6): 501-506.
[9] Sunday D M. A Very Fast Substring Search Algorithm[J]. Communications of the ACM, 1990, 33(3): 132-142.
[10] 張紅梅,范明鈺. 模式匹配BM算法改進[J]. 計算機應用研究, 2009, 26(9): 3249-3252.
[11] 萬曉榆, 楊 波, 樊自甫. 改進的Sunday模式匹配算法[J].計算機工程, 2009, 35(7): 125-126, 129.
[12] 錢 屹, 侯義斌. 一種快速的字符串匹配算法[J]. 小型微型計算機系統, 2004, 25(3): 410-413.
編輯 顧逸斐
Research and Improvement of BMH2C Single Pattern Matching Algorithm
WANG Yan-xia, JIANG Yan-xia, WANG Ya-gang, LI Ye
(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200082, China)
BMH2C algorithm combines BMH and BMHS algorithm. In BMH2C algorithm, the right shift distance of pattern string is determined by the double string, which is made of the character[] of the current window and the next character[+1]. BMH2C algorithm has better performance than BM, BMH and BMHS algorithm. Nevertheless, the right shift distance of pattern string in the BMH2C algorithm remains to be further increased, when the double string appears for one time or more than one time. Do like that, the number of window’s shift will be greatly reduced and the matching speed improved effectively. Therefore, an improved algorithm based on BMH2C algorithm is proposed. It takes the number of appearance in the pattern string of the double string[][+1] into account. And the equality relationship of character[+2] and the character which is followed the appropriate position of[][+1] in the pattern string is considered. The improved algorithm uses two right shift arrays and a pretreated array of the pattern strings. During the matching, the corresponding value of one of the two right shift arrays is selected as the right shift distance of current window, by judging the equality relationship of character[+2] and the corresponding character in the pretreated array. Experimental results show that the improved BMH2C algorithm is respectively 11.33% and 9.40% less than BMH2C algorithm on average in the same conditions, for the matching time and the number of window’s shift. With the algorithm, the matching speed is improved effectively
pattern matching; BMH2C algorithm; character string; right shift; pretreatment
1000-3428(2014)03-0298-05
A
TP301.6
國家自然科學基金資助項目(61074016, 61074087);上海市研究生創新基金資助項目(JWCXSL1202);上海市教育委員會科研創新基金資助項目(12ZZ144)。
王艷霞(1986-),女,碩士研究生,主研方向:3G/4G網絡通信技術,模式識別;江艷霞,講師;王亞剛,教授;李 燁,高級工程師。
2013-04-03
2013-06-02 E-mail:jiangyanxia@usst.edu.cn
10.3969/j.issn.1000-3428.2014.03.063

