二元函數(shù)S-粗集及其關(guān)系定理

呂昆，王磊

（1．山東城市建設(shè)職業(yè)學(xué)院基礎(chǔ)部，山東 濟南 250014；

2．山東省農(nóng)業(yè)科學(xué)院農(nóng)業(yè)質(zhì)量標(biāo)準與檢測技術(shù)研究所，山東 濟南 250100）

二元函數(shù)S-粗集及其關(guān)系定理

呂昆1，王磊2

（1．山東城市建設(shè)職業(yè)學(xué)院基礎(chǔ)部，山東 濟南 250014；

2．山東省農(nóng)業(yè)科學(xué)院農(nóng)業(yè)質(zhì)量標(biāo)準與檢測技術(shù)研究所，山東 濟南 250100）

給出了二元函數(shù)S-粗集的數(shù)學(xué)結(jié)構(gòu)和特性，提出了二元函數(shù)S-粗集與一元函數(shù)S-粗集、S-粗集、二元函數(shù)粗集、Pawlak粗集的關(guān)系定理。

二元函數(shù)S-粗集；一元函數(shù)S-粗集；二元函數(shù)粗集；關(guān)系定理

粗集的概念是由波蘭數(shù)學(xué)家Pawlak［1］提出的已得到了廣泛應(yīng)用。史開泉于2002年和2005年分別提出了S-粗集理論［2－3］和函數(shù)S-粗集理論［4－5］，將粗集理論從靜態(tài)推廣到了動態(tài)。本文在函數(shù)S-粗集，S-粗集以及杜素勤［6］提出的多元函數(shù)單向S-粗集的基礎(chǔ)上給出二元函數(shù)S-粗集及其相關(guān)定理的討論。

1 二元函數(shù)單向S-粗集及其對偶

約定：U為元素論域，XU為元素集，V（x）為一元函數(shù)論域，簡記作V，PV為一元函數(shù)集，D（x，y）為二元函數(shù)論域，記作D，函數(shù)u（x，y）記作u，二元函數(shù)集

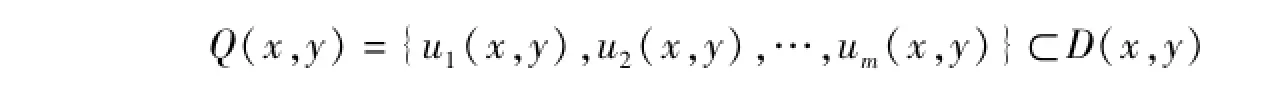
記作Q＝｛u1，u2，…，um｝D，二元函數(shù)等價類［u（x，y）］記作［u］。D中二元函數(shù)的定義域中的點可以是連續(xù)的也可以是離散的。

定義1.1 設(shè)D為二元函數(shù)論域，Q＝｛u1，u2，…，um｝D是二元函數(shù)集，如果存在變換f∈F，使得

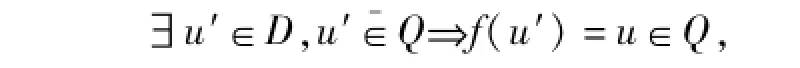
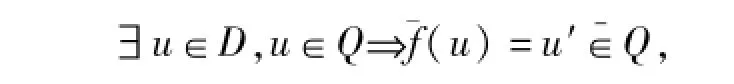
定義1.2 給定QD，如果

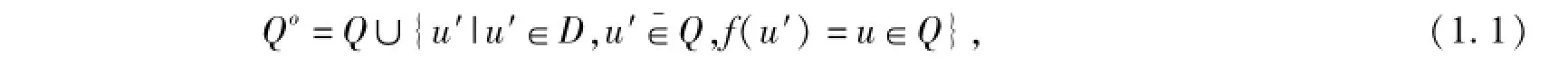
則稱Q0是Q的單向S-集合；如果

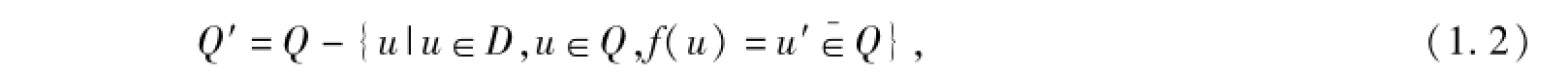
則稱Q′是Q的單向S-集合對偶；如果

則稱Qf為QD的f-擴張；如果

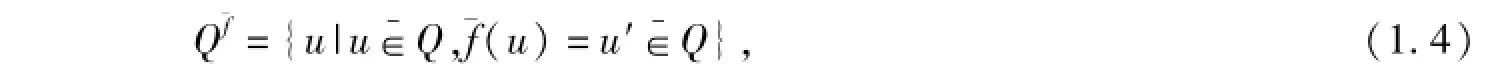
定義1.3 如果

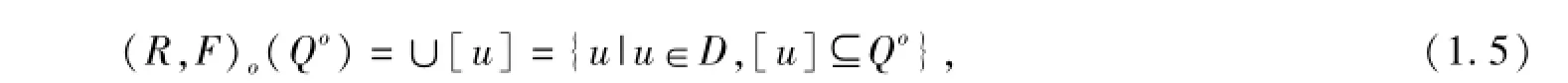
則稱（R，F(xiàn)）o（Qo）是QoD的下近似；如果

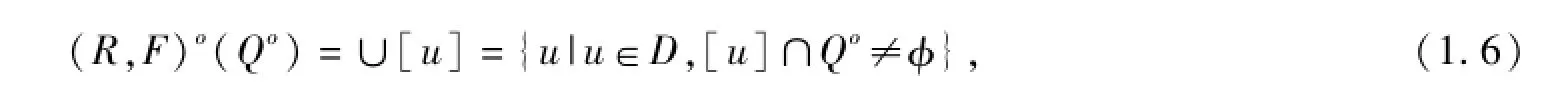
則稱（R，F(xiàn)）o（Qo）是QoD的上近似；如果

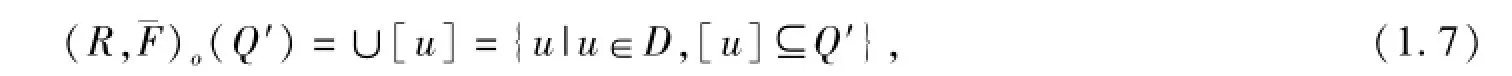
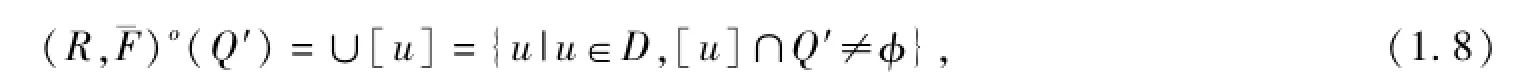
定義1.4 由（（R，F(xiàn)）o（Qo），（R，F(xiàn)）o（Qo）），組成的集合對稱作QoD的二元函數(shù)單向S-粗集，如果

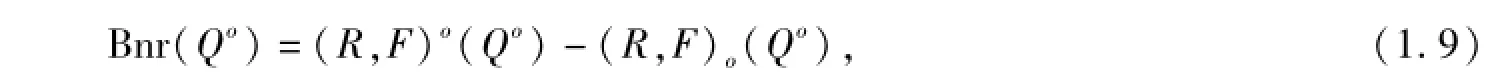
則稱Bnr（Qo）是QoD的邊界；

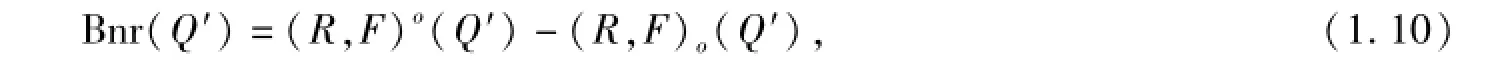
定義1.5 如果

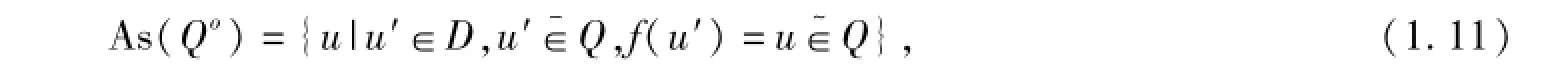
則稱As（Qo）是二元函數(shù)單向S-粗集（（R，F(xiàn)）o（Qo），（R，F(xiàn)）o（Qo））生成的副集合；如果

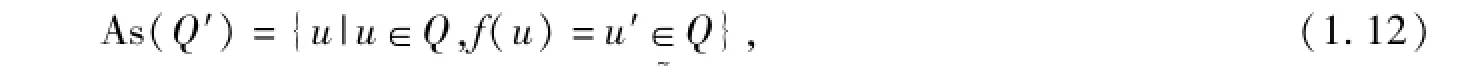
2 二元函數(shù)雙向S-粗集

定義2.1 如果

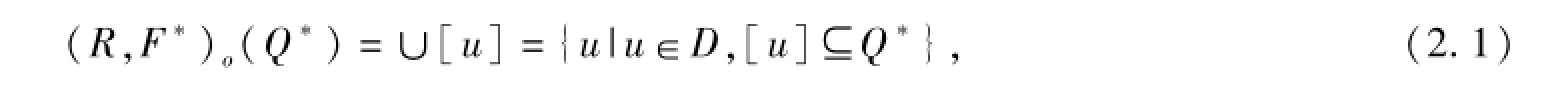
則稱（R，F(xiàn)*）o（Q*）是Q*D下近似；如果

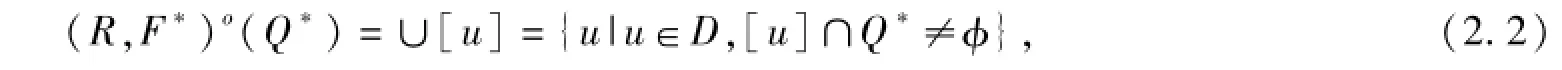
則稱（R，F(xiàn)*）o（Q*）是Q*D上近似，這里

定義2.2 則由（（R，F(xiàn)*）o（Q*），（R，F(xiàn)*）o（Q*））組成的集合對，則如果

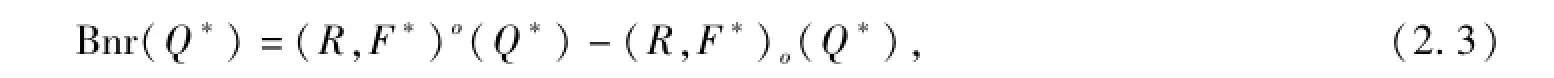
則稱作Q*D的二元函數(shù)雙向S-粗集，Bnr（Q*）是Q*D的邊界。

定義2.3 如果

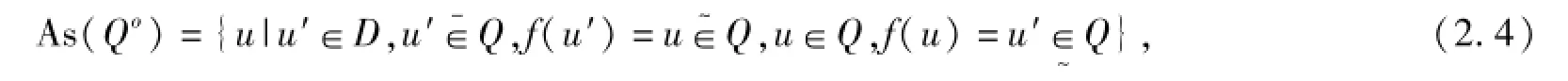
則稱As（Q*）是二元函數(shù)雙向S-粗集（（R，F(xiàn)*）o（Q*），（R，F(xiàn)*）o（Q*））生成的副集合。

3 二元函數(shù)S-粗集的相關(guān)定理

定理3.1 （α-一元函數(shù)等價類與α-元素等價類的α-二元函數(shù)等價類離散生成定理） 設(shè)［u］是D上的α-二元函數(shù)等價類，［u］＝｛u（k）｜k＝1，2，…，n，u（k）具有屬性集α｝，u（k）∈［u］的離散形式為：

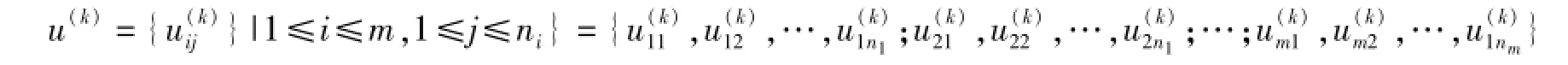
證明見文獻［6］。

定理3.2 （有限α-一元函數(shù)等價類與α-元素等價類生成定理） α-二元函數(shù)等價類生成有限個α-一元函數(shù)等價類［v］；α-二元函數(shù)等價類生成有限個α-元素等價類［x］。

定理3.3 （有限α-一元函數(shù)集與α-元素集生成定理） 有限α-二元函數(shù)集QD生成有限α-一元函數(shù)集PV；有限α-二元函數(shù)集QD生成有限α-元素集XU。

定理3.2 定理3.3的證明可由定理3.1得到。

定理3.4 （二元函數(shù)S-粗集與一元函數(shù)S-粗集關(guān)系定理） 設(shè)Po，P′，P*V分別為一元函數(shù)單向S-粗集，一元函數(shù)單向S-粗集對偶，一元函數(shù)雙向S-粗集，I＝｛1，2，…，m｝是有序正數(shù)集，則對i∈I，有

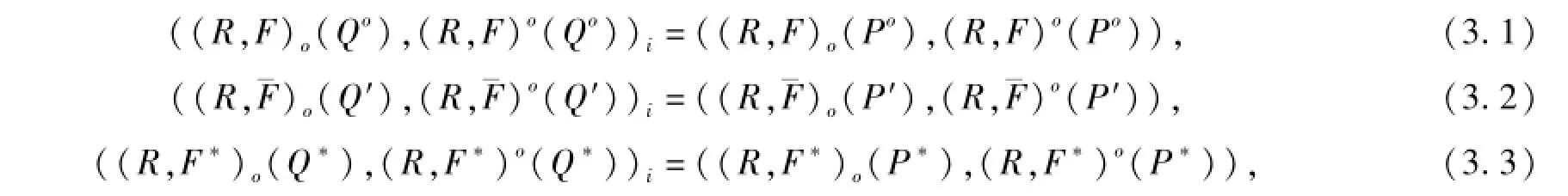
并且二元單向函數(shù)S-粗集生成一元函數(shù)單向S-粗集族

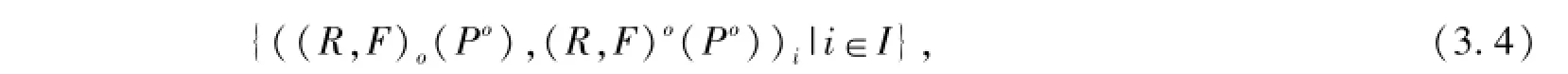
二元單向函數(shù)－粗集對偶生成一元函數(shù)單向－粗集對偶族

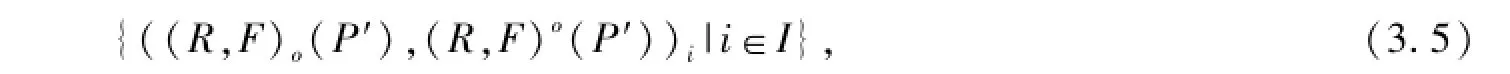
二元雙向函數(shù)－粗集生成一元函數(shù)雙向－粗集族

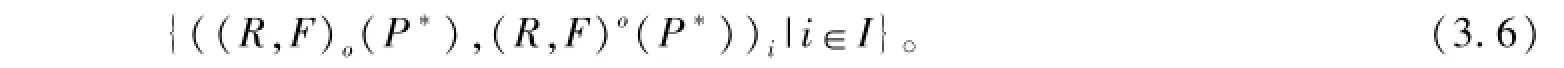
定理3.5 （二元函數(shù)S-粗集與S-粗集關(guān)系定理） 設(shè)Xo，X′，X*V分別為單向S-粗集，單向S-粗集對偶，雙向S-粗集，I＝｛1，2，…，m｝，J＝｛1，2，…，ni｝是兩個有序正數(shù)集，則對i∈I，j∈J，有

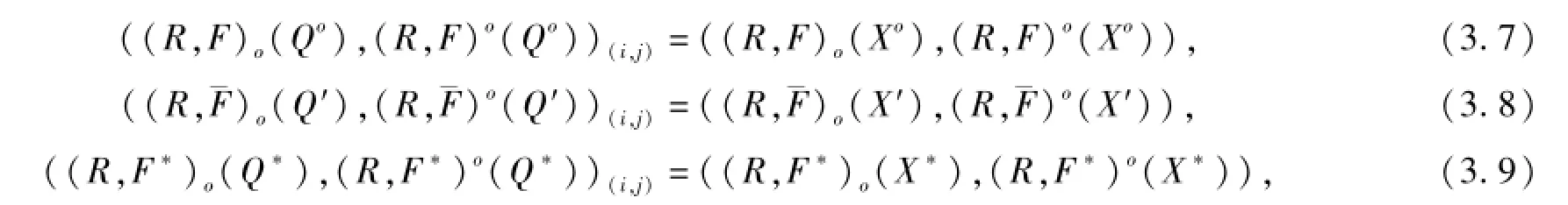
并且二元單向函數(shù)S-粗集生成單向S-粗集族

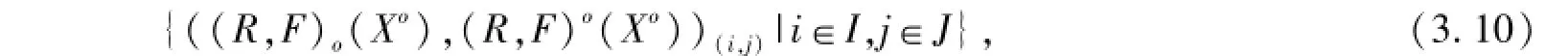
二元單向函數(shù)S-粗集對偶生成單向S-粗集對偶族

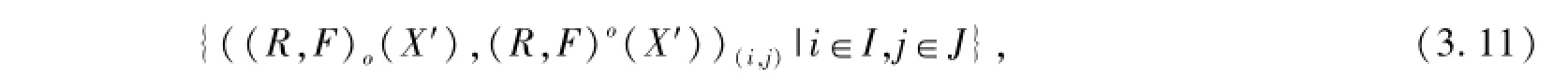
二元雙向函數(shù)－粗集生成雙向－粗集族

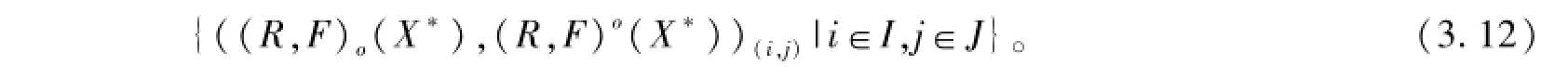
定理3.6 （二元函數(shù)S-粗集靜態(tài)生成二元函數(shù)粗集） 稱R－（Q），R－（Q）分別為QD的下近似和上近似，稱集合對R－（Q），R－（Q））為二元函數(shù)粗集，如果

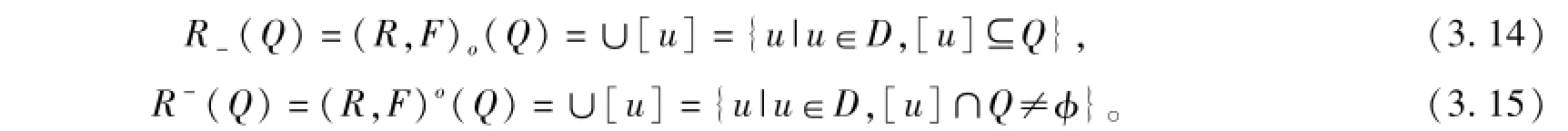
定理3.7 （二元函數(shù)S-粗集與Pawlak粗集關(guān)系定理）：

若F＝φ，i∈I＝｛1，2，…，m｝，j∈J＝｛1，2，…，ni｝，則

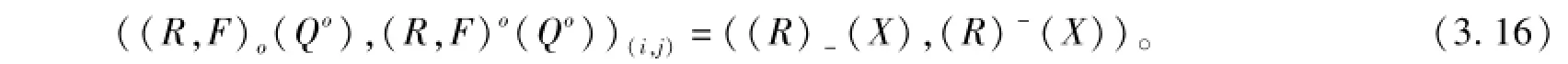
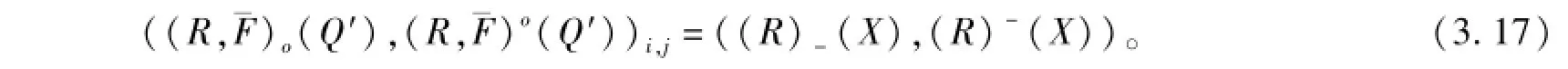
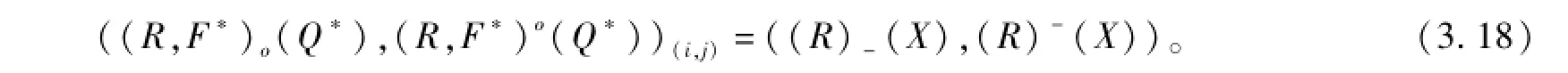
以上內(nèi)容在提出二元函數(shù)S-粗集與一元函數(shù)S-粗集關(guān)系定理時只討論了二元函數(shù)S-粗集在指標(biāo)i（1≤i≤m）上與一元函數(shù)S-粗集的關(guān)系定理，二元函數(shù)S-粗集在指標(biāo)j（1≤j≤ni）上與一元函數(shù)S-粗集的關(guān)系定理同理可得。

由此可見，Pawlak粗集是S-粗集的特例［2－3］，S-粗集是一元函數(shù)S-粗集的特例［4－5］，S-粗集是二元函數(shù)S-粗集的特例，一元函數(shù)S-粗集是二元函數(shù)S-粗集的特例；二元函數(shù)粗集是二元函數(shù)S-粗集的靜態(tài)生成，故Pawlak粗集是二元函數(shù)粗集的特例。

4 結(jié)語

一個系統(tǒng)的輸出特征可以用輸出狀態(tài)函數(shù)集來表示，輸出的狀態(tài)可以是一元函數(shù)集，也可以是多元函數(shù)集，本文是從二元函數(shù)的角度進行討論，以此為基礎(chǔ)可以進行二元以上的多元函數(shù)S-粗集的討論，為輸出狀態(tài)為多元函數(shù)的系統(tǒng)提供理論基礎(chǔ)。

［1］PAWLAK Z．Rough Sets［J］．International Jounal of Computer and Information Sciens，1982，11（5）：341－356．

［2］SHIK Q．S-rough sets and its applications in diagnosis-recognition for disease［J］．IEEE Proceedings of the First international Conference on Machine Learning and Cybernetics，2002，4（1）：50－54．

［3］史開泉，崔玉泉．S-粗集和它的一般結(jié)構(gòu)［J］．山東大學(xué)學(xué)報：理學(xué)版，2002，37（6）：471－474．

［4］SHIK Q．Function S-rough sets and function transter［J］．An Interation Journal Advance in Systems Science and Applications，2005，5（1）：1－8．

［5］史開泉．函數(shù)S-粗集［J］．山東大學(xué)學(xué)報：理學(xué)版，2005，40（1）：1－10．

［6］杜素勤．多元函數(shù)單向S-粗集［J］．甘肅聯(lián)合大學(xué)學(xué)報：自然科學(xué)版，2007，21（4）：4－7．

［7］史開泉，崔玉泉．S-粗集與粗決策［M］．北京：科學(xué)出版社，2006．

Two-variables function S-rough set and its relation theorem

LYU Kun1，WANG Lei2
（1．Department of Basis，Shandong Urban Construction Vocational College，Jinan 250014，China；2．Shandong Provincial Key Labo ratory of Food Quality，Institute of Quality Standard＆Testing Technology for Agroproducts，Shandong Academy of Agricultural Sciences，Jinan 250100，China）

We present the mathematical structure and characteristics of two-variables function S-rough sets．We also propose a relation theorem of two-varibles function S-rough sets with one-variable function S-rough sets，S-rough sets，twovariables function rough sets and Paw lak rough sets．

two-variables function S-rough set；one-variable function S-rough set；two-variables function rough set；relation theorem

O159

A

1002-4026（2014）01-0102-04

10.3976／j.issn.1002－4026.2014.01.018

2013-06-01

呂昆（1981－），女，講師，研究方向為粗系統(tǒng)理論與應(yīng)用。Email：lvkun1981＠163．com