基于雙線性對的可公開驗證多秘密共享方案

尚雪嬌,杜偉章

(長沙理工大學計算機與通信工程學院,長沙410114)

基于雙線性對的可公開驗證多秘密共享方案

尚雪嬌,杜偉章

(長沙理工大學計算機與通信工程學院,長沙410114)

現有可公開驗證多秘密共享方案只能由Lagrange插值多項式構造,且共享的秘密僅限于有限域或加法群。為解決上述問題,提出一個基于雙線性對的可公開驗證多秘密共享方案。該方案中每個參與者需持有2個秘密份額來重構多個秘密,并且在秘密分發的同時生成驗證信息。任何人都可以通過公開的驗證信息對秘密份額的有效性進行驗證,及時檢測分發者和參與者的欺騙行為。在秘密重構階段采用Hermite插值定理重構秘密多項式,并結合雙線性運算重構秘密。分析結果表明,在雙線性Diffie-Hellman問題假設下,該方案能抵抗內外部攻擊,具有較高的安全性。

雙線性對;秘密共享;多秘密共享;秘密份額;Hermite插值;雙線性Diffie-Hellman問題

1 概述

秘密共享是現代密碼學和信息安全的一個重要分支,在現實生活中有著廣泛的應用。Shamir[1]和Blakey[2]于1979年分別獨立提出了門限秘密共享方案,前者基于Lagrange插值多項式,后者基于射影幾何理論。為了防止不誠實的分發者和參與者的惡意行為,Chor[3]等人在1985年提出了可驗證的秘密共享方案。之后,Stadler[4]又提出了可公開驗證的秘密共享(PVSS)方案的概念。可公開驗證的秘密共享方案允許任何人對秘密份額的有效性進行驗證,并且驗證過程中不會泄漏秘密的相關信息。

近年來,隨著對秘密共享研究的深入,學者結合不同的公鑰密碼體制、數學模型、雙線性對技術等提出了各種各樣的秘密共享方案[5-8]。2010年,李大偉等人提出了一種使用IBE公鑰算法實現的可驗證秘密共享方案[9],該方案中秘密分發者將IBE私鑰作為共享秘密分發給參與者,參與者可以通過公開的驗證信息驗證秘密份額的正確性。田友亮等人構造了一個橢圓曲線上的信息論安全的可驗證秘密共享方案[10],利用雙線性對的雙線性性質,提高了方案中秘密份額驗證的有效性。文獻[11]提出了一個雙線性對上公開可驗證的多秘密共享方案,該方案利用雙線性對的性質實現了秘密份額的公開驗證,并且可以同時共享多個秘密。由于雙線性對具有很好的性質,越來越多的學者將其應用于秘密共享方案的研究[12-13]。

在一般的秘密共享方案中,共享的秘密都是有限域上[5]或加法群上[10]的,WU等人于2011年提出了一個基于雙線性對的可公開驗證秘密共享方案[14],方案中共享秘密s是乘法群上的,彌補了已有方案中共享秘密僅限于有限域和加法群上的不足,并利用雙線性對的性質對秘密份額的有效性進行了驗證,進而防止參與者的欺騙行為。本文在文獻[14]方案的基礎上,結合Hermite插值多項式構造了一個可公開驗證的多秘密共享方案,該方案可解決原方案一次秘密共享過程只能共享一個秘密的問題。

2 預備知識

2.1 雙線性對

定義1 設G1是階為q(q為素數)的加法群, G2是階為q的乘法群,若對任意的a,b∈,存在映射e:G1×G1→G2滿足以下性質,則稱該映射為雙線性映射:

(1)雙線性性:對任意P,Q∈G1,有e( aP,bQ)= e(P,Q)ab。

(2)非退化性:存在P,Q∈G1,使得e( P,Q)≠1。

(3)可計算性:對任意P,Q∈G1,存在有效算法計算e( P,Q)。

2.2 Diffie-Hellman問題

定義2 設G1和G2是階為素數q的加法群和乘法群,它們之間存在映射e:G1×G1→G2,P是G1的生成元,對任意的 a,b,c∈Z*q,定義如下數學難題:

(1)離散對數問題(DLP):給定(P,aP),求a。

(2)計算性 Diffie-Hellman(CDH)問題:給定(P,aP,bP),計算abP。

(3)雙線性 Diffie-Hellman(BDH)問題:給定(P,aP,bP,cP),計算e(P,P)abc∈G2。設算法A用來解決BDH問題,其優勢定義為ε,如果:

Pr(A(P,aP,bP,cP)=e(P,P)abc)≥ε

目前,還沒有有效的算法解決BDH問題。因此可以假設BDH問題是一困難問題。

2.3 Hermite插值

已知函數f(x)在n個互異點x1,x2,…,xn處的函數值f(x1),f(x2),…,f(xn)及一階導數f′(x1),f′(x2),…,f′(xn),可構造一個2n-1次多項式H2n-1(x)滿足以下插值條件:

其中,i=1,2,…,n。

此時的H2n-1(x)稱為Hermite插值多項式,它的一般表達式為:

其中,αj(x)和βj(x)稱為Hermite插值基函數:

3 方案描述

3.1 系統初始化

3.2 秘密分發

3.2.1 秘密份額的分發

秘密分發工作由D按以下步驟執行:

所以,rk=f(k-1),k=1,2,…,t。

(2)記f′(x)為f(x)的一階導數,則:

(3)D利用各參與者的身份信息為其計算偽秘密份額ui=f(IDi),vi=f′(IDi),計算并公開系數承諾Aj=ajP,j=0,1,…,2t-1,易知A0=f(0)P,A1= f′(0)P。

3.2.2 秘密份額的驗證

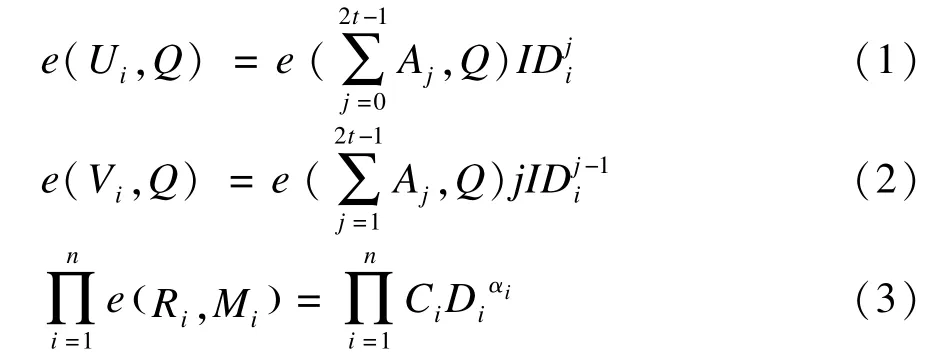
3.3 秘密重構

秘密重構的過程如下:

(1)參與者Pi利用自己的私鑰xi計算:

若t個參與者的秘密份額均能通過驗證,則利用2t個秘密份額s1j(j=1,2,…,t)和s2j(j=1,2,…,t),根據雙線性對的性質和Hermite插值定理可得:

其中:

由于rk=f( k-1),因此可以得出:

4 方案分析

4.1 正確性分析

驗證式及秘密重構的正確性分析如下:

(1)驗證式的正確性

首先證明式(1)和式(2)的正確性:

由于 Ui=uiP,Vi=viP,ui=f(IDi),vi= f′(IDi),則:

由以上2個等式成立可知,分發者D為參與者Pi分發的偽秘密份額(ui,vi)是有效的。

下面證明式(3)的正確性:

因此,驗證式(3)是正確的,即包含參與者秘密份額相關信息的數據(Ci,Di)是有效的。

驗證式(4)的正確性:

因此,式(4)是正確的,可以用來驗證參與者提供的秘密份額的有效性。

(2)秘密重構的正確性

參與者Pi利用自己的私鑰xi,由Ci=e(Ri,Ppub)ui和Di=e(Ri,Ppub)vi得到秘密份額s1i=e(Ppub,Ppub)ui, s2i=e(Ppub,Ppub)vi。當重構秘密Sk(k=1,2,…,t)時, t個參與者P1,P2,…,Pt合作共同計算:

又因為rk=f(k-1),所以:

這樣即可得到共享的t秘密S1,S2,…,St。

4.2 安全性分析

定理2 若BDH假設成立,則任何少于t個參與者合作都不能重構秘密s1,s2,…,st。

(2)隨機選取t-1組整數:(f(d1),f′(d1)), (f(d2),f′(d2)),…,(f(dt-1),f′(dt-1)),再結合已經確定的(f(0),f′(0)),由Hermite插值定理可知,這樣便確定了2t-1次多項式f(x)。

(3)計 算 Ci=e(Ri,Ppub)f(di),Di=e (Ri,Ppub)f′(di),Ui=f(di)P,Vi=f′(di)P,i=1, 2,…,t-1。

(4)由于f( 0)和f′(0)隱含在A0和A1中,因此攻擊者A雖然固定了f(x),卻無法重構它,故不能計算f(t),f(t+1),…,f(n)的值。然而,由A0=aP, A1=bP,Ui=f(di)P,Vi=f′(di)P,i=1,2,…,t-1,A可以得到如下的方程組:

其中,i=1,2,…,t-1。

解該方程組可以求出A2,A3,…,A2t-1。然后,A便可利用求出的A0,A1,…,A2t-1計算Ui(i=t,t+1,…,n)和Vi(i=t,t+1,…,n)的值。

(5)令參與者Pi的公鑰Ri=x′iPpub,i=1,2,…, n。由于 Ci=e(Ri,Ppub)ui=e(x′iPpub,Ppub)ui= e(x′icP,Ppub)f(di),Ui=f(di)P,因此 Ci=e (Ui,Ppub)cx′i,i=1,2,…,n。同理,可以得到Di=e (Vi,Ppub)cx′i,i=1,2,…,n。

這樣,所有的參數設置完成,即成功建立了一個模擬的多秘密共享系統。攻擊者A將這些信息提供給t-1個成員P1,P2,…,Pt-1,根據假設,這t-1個成員可以重構秘密 Sk=e(Ppub,Ppub)rk。當 k=1時,由秘密S1=e(Ppub,Ppub)r1=e(Ppub,Ppub)f(0), Ppub=cP,f(0)P=aP,可推出 e(P,P)acc=e (Ppub,Ppub)f(0),這說明BDH問題是可以求解的,即BDH假設不成立。因此,若BDH假設成立,任何少于t個參與者合作不能重構秘密s1,s2,…,st。

5 結束語

本文基于橢圓曲線上的離散對數問題和雙線性Diffie-Hellman假設,并結合Hermite插值定理構造了一種新的可公開驗證多秘密共享方案。秘密分發不需要安全通道,僅利用雙線性對的性質即可實現秘密份額的公開驗證,每個參與者只需持有2個秘密份額就可以重構多個秘密。通過對方案正確性和安全性的分析可知,該方案滿足可公開驗證多秘密共享方案的特性。同時,Hermite插值多項式的引入,為可公開驗證多秘密共享方案的研究提供了一種新的途徑。然而,該方案中較多的雙線性運算影響了其運行效率,因此,提高多秘密共享方案的效率是下一步的工作重點。

[1] Shamir A.How to Share a Secret[J].Communications of the ACM 1979,22(11):612-613.

[2] Blakley G R.Safeguarding Cryptographic Keys[C]// Proceedings of National Computer Conference. New York,USA:[s.n.],1979:313-317.

[3] Chor B,Goldwasser S,Micali S,et al.Verifiable Secret Sharing and Achieving Simultaneity in the Presence of Faults[C]//Proceedings of the 26th IEEE Symposium on Foundations of Computer Science.[S.1.]:IEEE Press,1985:383-395.

[4] Stadler M.Publicly Verifiable Secret Sharing[C]// Proceedings of Cryptology-Eurocryptp'96.Berlin, Germany:Springer-Verlag,1996:191-199.

[5] Kaya K,Selcuk A.A Verifiable Secret Sharing Scheme Based on the Chinese Remainder Theorem[C]// Proceedings of INDOCRYPT'08.Berlin,Germany: Springer-Verlag,2008:414-425.

[6] 步山岳,王汝傳.一種可驗證和高效的多秘密共享門限方案[J].計算機科學,2011,38(1):100-103.

[7] 田有亮,彭長根.基于雙線性對的可驗證秘密共享方案[J].計算機應用,2007,27(12):125-127.

[8] 譚曉青.高效的可驗證多秘密共享方案[J].計算機工程與應用,2009,45(12):33-35.

[9] 李大偉,楊 庚,朱 莉.一種基于身份加密的可驗證秘密共享方案[J].電子學報,2010,38(9):2060-2065.

[10] 田友亮,馬建峰,彭長根,等.橢圓曲線上的信息論安全的可驗證秘密共享方案[J].通信學報,2011,32 (12):96-102.

[11] 張建中,張艷麗.一個雙線性對上公開可驗證多秘密共享方案[J].計算機工程與應用,2011,47(25): 82-84.

[12] Tian Youliang,Peng Changgen,Ma Jianfeng.Publicly Verifiable Secret Sharing Schemes Using Bilinear Pairings [J].International Journal of Network Security,2012,14 (3):142-148.

[13] Li Fei,Gao Wei,Wang Yi-lei.An Efficient Certificateless Threshold Decryption Schemes Based on Pairings[J]. Journal of Computers,2012,7(12):2987-2996.

[14] Wu Tsu-Yang,Tseng Yuh-Min.A Pairing-based Publicly Verifiable Secret Sharing Scheme[J].Journal of Systems Science and Complexity,2011,24(1):186-194.

編輯 索書志

Publicly Verifiable Multi-secret Sharing Scheme Based on Bilinear Pairings

SHANG Xue-jiao,DU Wei-zhang
(College of Computer and Communication Engineering,Changsha University of Science and Technology,Changsha 410114,China)

In order to solve the problems that the previous publicly verifiable multi-secret sharing schemes can be constructed only by Lagrange interpolation polynomial and the shared secret is limited to the finite field or additive group,a publicly verifiable multi-secret sharing scheme based on bilinear pairings is proposed.In the scheme,each participant has to hold two shares for reconstructing multiple secrets,and the verification information is generated in the process of secret distribution.According to public verification information,anyone can verify the validity of secret shares. Cheating of dealer and participants can be detected in time.In the secret reconstructing process,Hermite interpolation theorem is used to reconstruct the secret polynomial,and bilinear operation is combined to reconstruct the secret.Under the assumptions of Bilinear Diffie-Hellman Problem(BDHP),the analysis result shows that this scheme can resist internal and external attacks and is a secure and efficient multi-secret sharing scheme.

bilinear pairings;secret sharing;multi-secret sharing;secret share;Hermite interpolation;Bilinear Diffie-Hellman Problem(BDHP)

1000-3428(2014)09-0155-04

A

TP309

10.3969/j.issn.1000-3428.2014.09.031

尚雪嬌(1988-),女,碩士研究生,主研方向:信息安全;杜偉章,教授、博士。

2013-08-19

2013-10-10E-mail:wbjsxj_2012@163.com