泛化改進的局部切空間排列算法

趙遼英,李富杰,厲小潤

(1.杭州電子科技大學計算機應用技術研究所,杭州310018;2.浙江大學電氣工程學院,杭州310027)

泛化改進的局部切空間排列算法

趙遼英1,李富杰1,厲小潤2

(1.杭州電子科技大學計算機應用技術研究所,杭州310018;2.浙江大學電氣工程學院,杭州310027)

改進的局部切空間排列(ILTSA)算法解決了當樣本稀疏、分布不均勻或數據流密度曲率變化較大時,局部切空間排列算法不能揭示流形結構的問題,用于人臉識別能提取更好的低維特征,但不能有效處理不斷增加的數據集的問題。為此,提出一種可泛化的ILTSA(GILTSA)算法。結合類別信息定義樣本間的距離實現各樣本的近鄰集選擇,基于ILTSA算法求解訓練樣本集的低維流形,對每個新樣本尋找其在訓練樣本集中的最近鄰,然后根據ILTSA算法原理求得其近似低維流形。在ORL、Yale和埃塞克斯大學人臉庫上的實驗結果表明,與主成分分析算法和線性局部切空間排列算法等相比,GILTSA算法具有更好的識別率。

流形學習;局部切空間排列;泛化;特征提取;人臉識別

1 概述

人臉識別技術是生物特征鑒別技術的一個主要方向,在安全保衛、信息安全和司法檢驗等領域具有十分重要的意義,多年來一直是一個研究熱點。由于人臉是易變的、非剛性的,很難用固定的模型進行描述,因此特征提取是人臉識別技術中一個基本而又十分重要的環節。

目前提出的特征提取方法總體上可以分為線性和非線性2類,其中經典的線性特征提取算法包括主成分分析(Principal Component Analysis,PCA)［1］、獨立成分分析(Independent Component Analysis,ICA)［2］和線性描述分析(Linear Discriminant Analysis,LDA)［3］等。這些算法的特點是通過計算原始空間中存在的線性結構來獲得原始數據的低維表示,容易實現并得到了廣泛的應用,但是并不能揭示潛在的流形結構。近年來的研究成果表明,人臉圖像很可能位于一個非線性流形上［4-7］,許多有效的流形學習算法被發現并廣泛應用。2000年Science雜志同一期發表的2篇文章分別提出了等距映射(Isometric Mapping,ISOMAP)［8］和局部線性嵌入(Locally Linear Embedding,LLE)［9-10］算法,其中, ISOMAP以測地線距離表示原始數據中的相似性關系,通過全局映射求得低維流形,LLE則采用局部鄰域的線性重構系數描述其幾何結構,求得低維流形保持局部幾何結構,是一種局部算法。文獻［11］提出拉普拉斯特征映射(Laplacian Eigenmap,LE),采用一個無向有權圖描述數據,利用圖拉普拉斯的性質把數據從高維映射到低維空間。文獻［12-13］提出的局部切空間排列(Local Tangent Space Alignment,LTSA)通過局部空間PCA變換得到局部切空間坐標;然后經過一系列變換將局部切空間坐標轉換為全局切空間坐標,得到低維嵌入。LTSA是一種很好的流形學習算法,但當數據是稀疏或者分布不均勻、整個數據流形結構有很大的曲率時, PCA可能會有一個壞的結果,LTSA也就不能真實地揭示數據的本質結構。文獻［14］針對LTSA的問題,提出了改進的LTSA(ILTSA)算法,將樣本本身作為局部切空間的中心而不是其k個近鄰點的均值為中心,并且在局部切空間的目標函數中通過一個權值來反映局部近鄰距離。

上述這些流形學習算法都存在2個問題,一個是在k近鄰選擇過程中沒有考慮類別信息,降維后識別率不高,另一個最主要的問題是它們都不具有泛化能力,對新樣本不能進行有效的降維處理。解決第一個問題的辦法主要是在k近鄰選擇中將類別信息結合到距離度量中,如文獻［15］提出了增強監督的LLE(Enhanced Supervised LLE,ESLLE)算法,根據2個樣本是否同類定義了不同的距離度量方式。眾多學者對第2個問題進行了研究,提出了3類方法,第 1類是線性化方法,如鄰域保護嵌入(Neighborhood Preserving Embedding,NPE)［16］、局部保局投影(Locality Preserving Projections,LPP)［17］和線性局部切空間排列(Linear Local Tangent Space Alignment,LLTSA)［18］分別是LLE、LE和LTSA對應的線性化方法;第2類是最近鄰近似方法,如文獻［19］研究了LTSA算法的泛化問題,提出了可泛化的LTSA(GLTSA)方法;第3類是圖嵌入方法。圖嵌入為多種降維算法提供了一個統一框架,每種降維算法可以看作核化的圖嵌入,對應泛化算法的關鍵是核函數的確定。文獻［20］對ISOMAP、LE、 LLE和LTSA等基于圖嵌入框架的核函數及泛化進行了深入研究,其中LTSA的核函數還需要繼續驗證。本文主要基于最近鄰近似方法,提出了一種可泛化的ILTSA(GILTSA)算法,首先對訓練樣本集用有監督的k近鄰選擇方法確定ILTSA算法中各樣本的k近鄰集,然后基于ILTSA算法求解樣本集的低維流形,對每個新樣本尋找其在訓練樣本集中的最近鄰,然后根據ILTSA算法原理求得其近似低維流形。

2 GILTSA算法描述

GLITSA算法主要分3個步驟完成,先用有監督的方法尋找各樣本的k近鄰,然后基于ILSTA求得訓練樣本集的低維流形,最后在訓練樣本集中找到新樣本的最近鄰,用最近鄰近似投影方法得當新樣本的低維流形。

2.1 有監督的近鄰選擇

k近鄰選擇首先需要計算樣本間的距離。為了充分利用樣本數據的類別信息,在對樣本點xi進行k近鄰選擇時,利用類別信息修改歐式距離矩陣D,以確定更好的近鄰點。

對于一對數據(xi,Li)和(xj,Lj),{xi,yj}∈RD, Li和 Lj分別是 xi和 xj的類別信息,定義如下距離［12］:

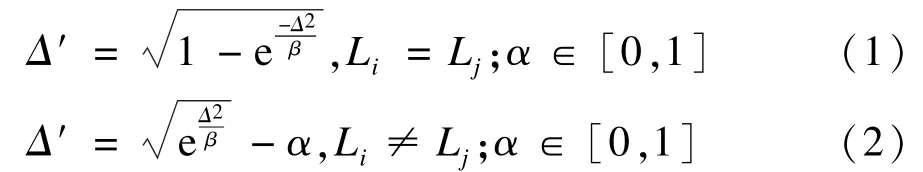
其中,Δ是樣本點xi和xj之間未包含類別信息的歐式距離;參數β控制距離Δ的增長速度,通常取β等于所有樣本數據中任意兩點間歐式距離的均值。

給定訓練樣本集X=［x1,x2,…,xN］,對每個樣本,將其與其他樣本間的距離從小到大排序,確定k近鄰。

2.2 基于ILTSA的訓練樣本集低維嵌入

設訓練樣本xi的k個近鄰點集合為Xi=［xi1, xi2,…,xik］,為了保持每個樣本點xi在低維空間中的局部結構,ILTSA算法［11］通過對映射距離加權和以xi作為其近鄰點的局部中心來減弱樣本點分布不均的影響。構造局部嵌入目標函數:

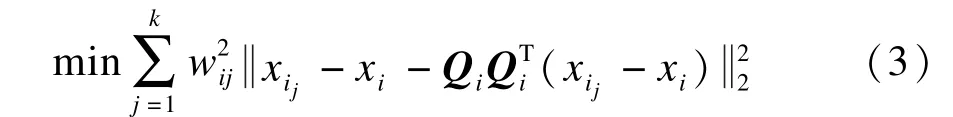
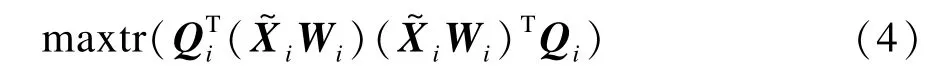
Qi={Qi1,Qi2,…,Qid}是矩陣(iWi)(iWi)T的d個最大特征值所對應的特征向量,xij在局部切空間的投影為ij=(xij-xi)。設Y={y1,y2,…, yN}是樣本X=［x1,x2,…,xN］在全局坐標系統下的投影結果,yij是xij在全局坐標系統下對應的點,yi是xi在全局坐標系統下對應的點。假設在~θij和yij有唯一的仿射變換,則有:

其中,j=1,2,…,k;i=1,2,…,N;εij表示誤差。

為了保持在低維特征空間中局部幾何結構,需要使得重構誤差函數ε(y)最小:

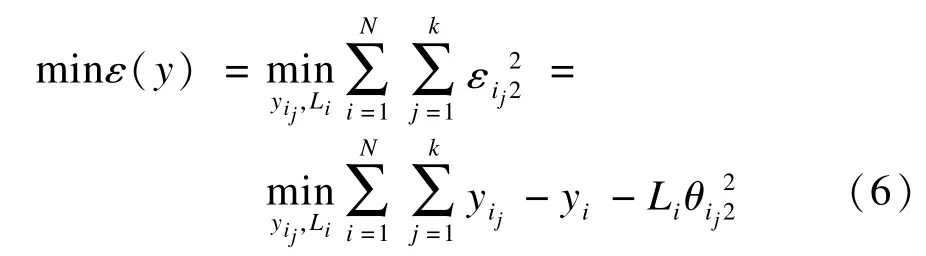
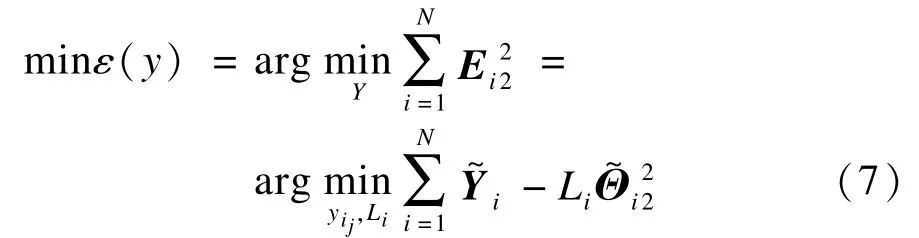
再次轉化,則式(7)等于:

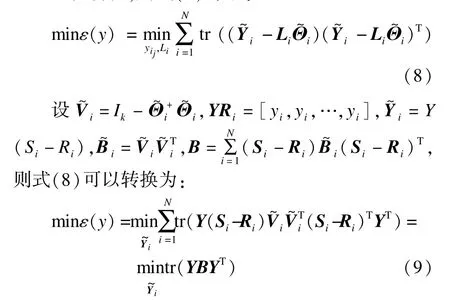
通過下式構建排列矩陣B:

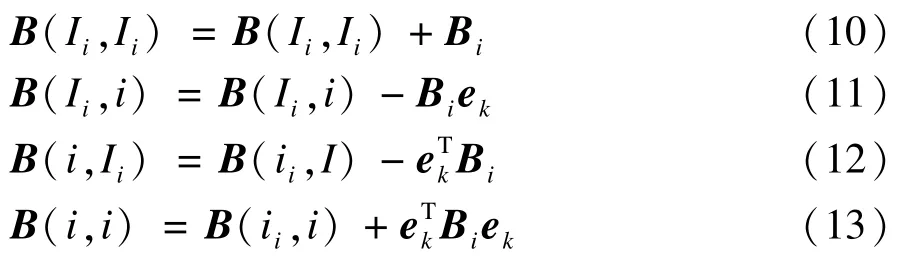
B的初始化值為0,Bi={i1,i2,…,ik}表示xi的k個近鄰在排列矩陣中的索引。

計算矩陣B的Fd+1個最小特征值所對應的特征向量,選擇其中第2小到第Fd+1個特征值對應的特征向量得到樣本數據的低維表示為 Y=［u2, u3,…,uFd］′。

2.3 新樣本點的最近鄰近似投影

對于一個新的點xn(n＞N),找到其在訓練樣本集中的最近鄰點xi,設Xi=［xit,xit+1,…,xik］和Yi=［yit,yit+1,…,yik］分別是xi的k個近鄰點和它在低維坐標空間中相對應的點。根據ILTSA算法原理可以得到:

通過最近鄰點xi低維投影點近似得到xn(n＞N)對應的低維空間投影點:

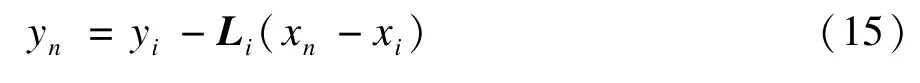
3 實驗結果與分析

為了評估GILTSA算法的優劣,采用ORL人臉數據庫(http://cvc.yale.endu/projects/yalefaces/yalefaces.html)、Yale人臉數據庫(http://cobweb.ecn.purdue.edu/～aleix/aleix_face_DB.html)和埃塞克斯大學人臉數據庫(http://cswww.essex.ac.uk/mv/allfaces/),將PCA這種非流形學習算法、LLTSA、GLTSA這2種流形學習算法、Baseline方法和GILTSA算法進行人臉識別實驗比較,分類算法采用k近鄰分類法(KNearest Neighborhoods,KNN),實驗中k取值為8。由于計算機內存的限制,這些人臉數據庫中的人臉圖片無法直接用于實驗。因此,在實驗時這些圖片被轉化為32×32像素的256級灰度圖片,每一幅圖片在圖像空間中將會表示成一個1 024維的向量。Baseline方法對原始數據不做降維處理,直接用于分類。GILTSA、LLTSA和GLTSA的第一步k近鄰選擇都采用監督的方法。這3個方法都有3個參數需要確定,分別為近鄰數k、局部流形維度d和全局流形維度Fd。由于LLTSA、GLTSA、GILTSA算法對不同的數據庫對應的最佳參數不同,因此先通過多次實驗確定不同方法對應不同數據庫的相對最佳參數。對每個人臉數據庫,分別做2個實驗:(1)對于GILTSA、LLTSA、GLTSA算法固定所選擇的近鄰數k和局部降維維度d,測試最終降維維度Fd與識別率Rate的關系,由于人臉圖像是固定選取的,因此當識別率達到最大值時的最終的流形降維維度Fd并不一定會在隨機選取的情況下平均識別率最大,但是可以確定隨機選取人臉圖像時使識別率達到最大的最終的流形降維維度Fd區間。本著應用的需要,分別實驗在Fd的最佳區間內選取使得各個算法在隨機選取圖片的條件下平均識別率達到最大時的參數來獲得最佳參數。(2)相對最佳參數下多次實驗的平均識別率、最小和最大識別率的比較。另外實驗中的數據均無單位。

3.1 ORL人臉數據庫實驗結果與分析

ORL人臉數據庫共由40個不同的人臉部圖像組成,每個人包含10幅圖像,每幅圖像的大小為112×92像素,每幅人臉的光照條件、人臉表情、面部細節各不相同,但是背景相同。圖1給出了ORL數據庫中某人的10副圖像。

圖1 ORL數據庫樣本示例

分別對每個人選取3個、5個訓練樣本,余下的作為測試樣本,設置近鄰數參數k=10,局部流形維度d=3的情況下識別率Rate和全局子空間維度Fd的關系如圖2所示。從圖2(a)中可以看到,當每個人選取3個訓練樣本時,對于PCA算法,當全局子空間維度逐步增大時識別率不斷增大,在Fd=15左右趨于平緩,雖然仍然有浮動,但是變化不大,平均識別率在0.7左右。對于GILTSA、LLTSA、GLTSA算法,可以看到在Fd=35～60之間,平均識別率達到最高值為0.75左右,但是在Fd＞60時,識別率不斷下降,因此對于GILTSA、LLTSA、GLTSA更高的降維維度并不會增大識別率。這一點從圖2(b)中也可以看到。

在選取合適的參數使LLTSA、GILTSA、GLTSA、PCA算法達到最大識別率的條件下,對于不同人臉隨機選取3個、5個訓練樣本做79次人臉識別,其中,最佳識別率,平均識別率和最小識別率如表1所示,括號中為全局子空間維度。從表1可以看到,相對于PCA、LLTSA、GLTSA、GILTSA算法,GILTSA算法在選取3個訓練樣本和5個訓練樣本時最小識別率、平均識別率和最大識別率都要高一些。

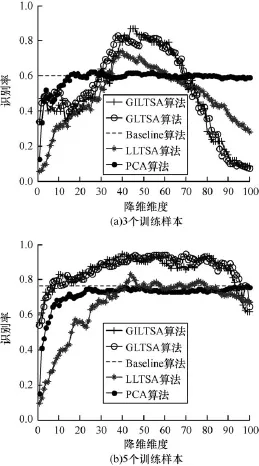
圖2 識別率與子空間維度的關系(ORL)

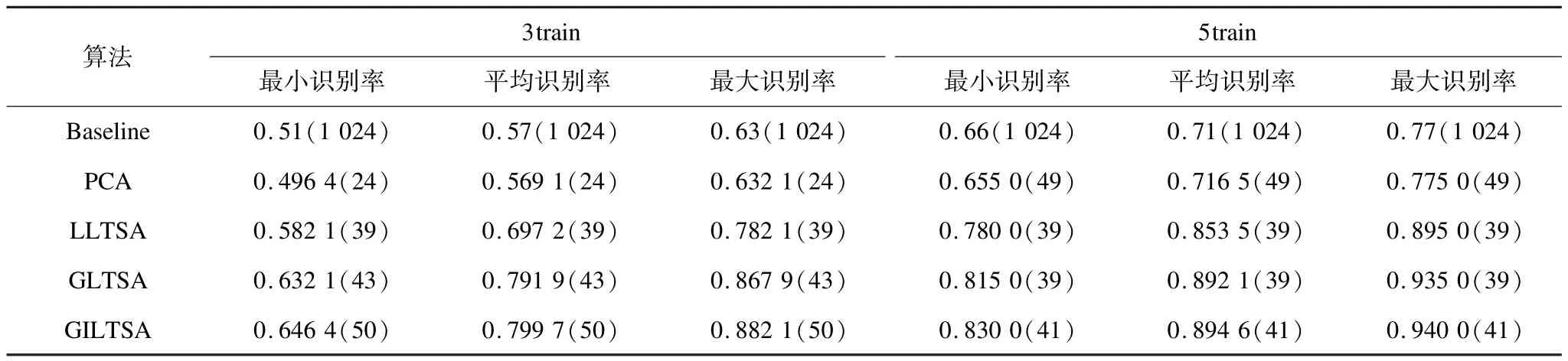
表1 ORL人臉庫5種算法的識別率比較

3.2 Yale人臉數據庫實驗結果與分析

由耶魯大學計算機視覺與控制中心創建,包含15位志愿者的165幅灰度圖片,每個人11幅圖片。每個人的11圖片中包含戴眼鏡、不戴眼鏡、左邊亮、右邊亮、正常表情、悲傷、驚訝、疲勞和眨眼等變化。圖3展示了其中一個人的所有圖片。

圖3 Yale數據庫樣本示例

同樣做2個實驗。分別對每個人選取3個、5個訓練樣本,余下的作為測試樣本,設置近鄰數參數k=11,局部流形維度d=4的情況下識別率Rate和全局流形維度Fd的關系如圖4所示。從圖4(a)中可以看到,當每個人選取3個訓練樣本時,對于PCA算法,當最終降維維度逐步增大時,識別率不斷增大,在Fd=10左右趨于平緩,雖然仍然有浮動,但是變化不大,平均識別率在0.5左右。對于GILTSA、LLTSA、GLTSA算法,可以看到在Fd=6～25之間平均識別率達到最高值為0.65左右,但是在Fd＞25時,GILTSA和GLTSA算法識別率不斷下降,LLTSA算法變化不大。從圖4(b)中可以看到,GILTSA、LLTSA、GLTSA算法在Fd=23～35是識別率達到最大為0.90左右。

在選取使LLTSA、GILTSA、GLTSA、PCA算法達到最大識別率參數的條件下,分別79次對于不同人臉隨機選取3個訓練樣本、8個測試樣本和5個訓練樣本、6個測試樣本,其中,最佳識別率,平均識別率和最小識別率如表2所示。從表2中可以看到,在隨機選取3個訓練樣本、8個測試樣本時,GILTSA算法與其他算法相比較,平均識別率、最大識別率、最小識別率相對都要大。在隨機選取5個訓練樣本、6個測試樣本時GILTSA算法,最大識別率要小于GLTSA和LLTSA算法,但是大于PCA算法,最小識別率要大于其他算法。因此,可以說明GILTSA算法相對于其他算法穩定性更好。

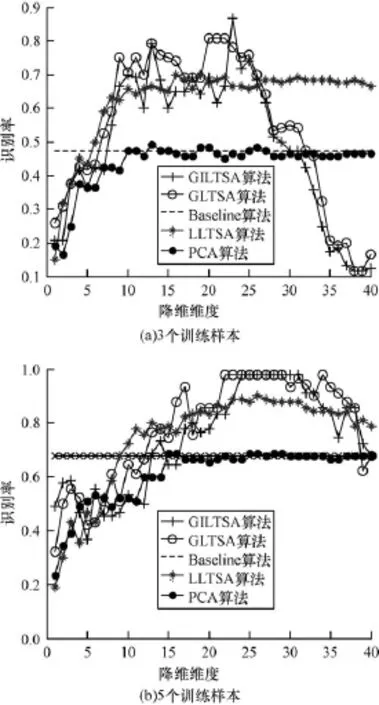
圖4 識別率與降維維度的關系(Yale)

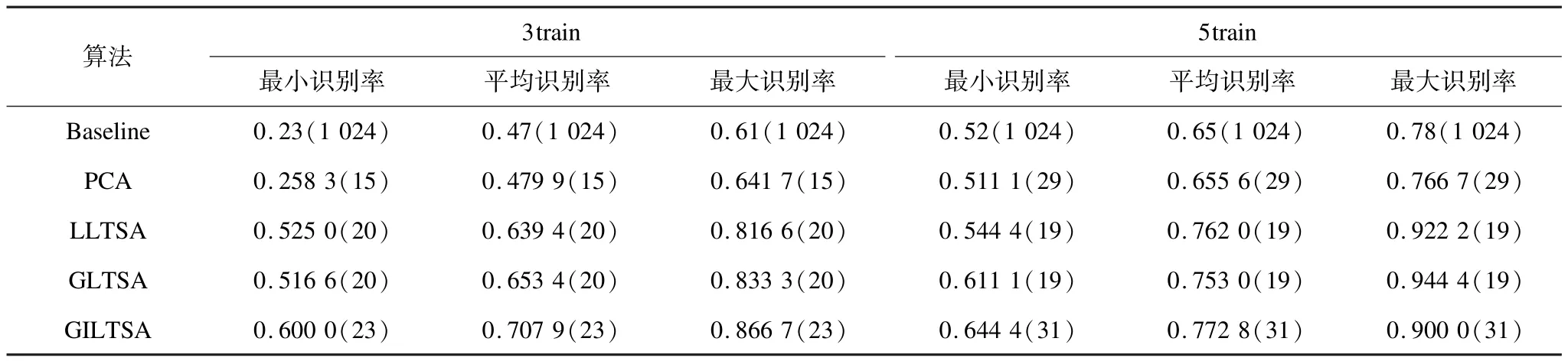
表2 Yale人臉庫5種算法識別率的比較

3.3 埃塞克斯大學人臉數據庫實驗結果與分析

由埃塞克斯大學的 Libor Spacek博士主持設計,整個人臉庫包含 faces94、faces95、faces96、grimace等5個部分。選取其中的grimace人臉庫, grimace人臉庫包含18人,分為男性、女性2個部分,每人20幅圖片。每幅圖片的大小為118×200像素。圖像的亮度變化較小。圖像中人臉的傾斜度、角度和姿勢變化比較微小。主要是嘴部和表情的變化。實驗中選取其中18人,每人選取20幅圖像。圖5展示了其中一個人的所有圖片。

圖5 grimace數據庫部分樣本示例

圖6顯示了分別對每個人選取3個、5個訓練樣本,余下的作為測試樣本設置近鄰數參數k=12、局部流形維度d=3的情況下識別率Rate和全局子空間維度Fd關系。從圖6(a)中可以看到,當每個人選取3個訓練樣本時,對于PCA算法,當全局子空間維度逐步增大時識別率不斷增大,在Fd=10左右趨于平緩,雖然仍然有浮動,但是變化不大,平均識別率在0.6左右。對于GILTSA、LLTSA、GLTSA算法,可以看到在Fd=15～25之間平均識別率達到最高值為0.85左右,但是在Fd＞30時,識別率不斷下降,因此對于GILTSA、LLTSA、GLTSA更高的降維維度并不會增大識別率。這一點從圖6(b)中也可以看到。

選取使LLTSA、GILTSA、GLTSA、PCA算法達到最大識別率的參數的條件下,分別79次對于不同人臉隨機選取3個訓練樣本、17個測試樣本和5個訓練樣本、15個測試樣本,其中,最佳識別率,平均識別率和最小識別率如表3所示。從表3中可以看到,隨機選取3個訓練樣本、17個測試樣本和5個訓練樣本、15個測試樣本時,GILTSA算法相對于其他算法,最佳識別率、平均識別率和最小識別率相對要更高一些。

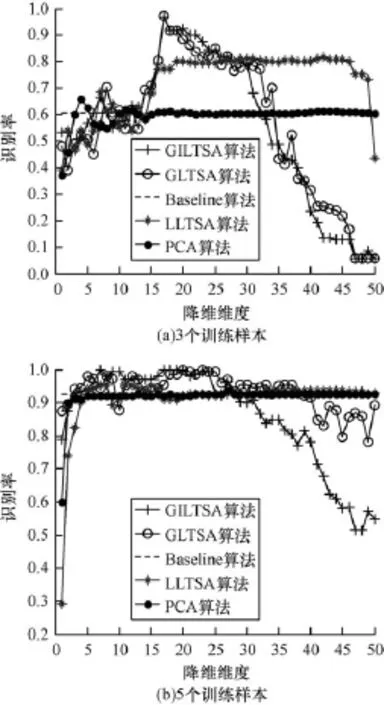
圖6 識別率與降維維度的關系(grimace)

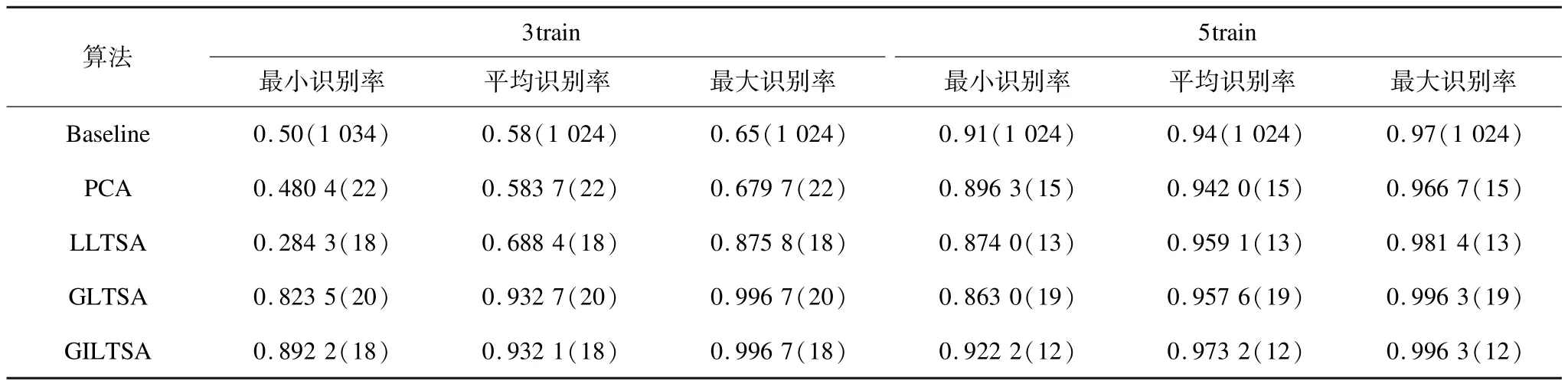
表3 grimace人臉庫5種算法識別率的比較

4 結束語

本文主要研究ILTSA算法的泛化問題,提出了一種基于最近鄰近似投影的可泛化ILTSA算法,并用于人臉識別。GILTSA算法與ILTSA算法相比。該算法改進的地方主要有以下2點:(1)結合類別信息定義樣本間的距離實現各樣本的近鄰集選擇; (2)對每個新樣本尋找其在訓練樣本集中的最近鄰,然后根據ILTSA算法原理求得其近似低維流形。在ORL、Yale和埃塞克斯大學人臉庫上的實驗結果表明,GILTSA方法與其他方法相比,具有更好的識別率。

在實驗的過程中發現:(1)GILTSA、GLTSA和LLTSA算法在求局部切空間的坐標時對于近鄰點的排列要求很高,不同的排列方式所得到的最終識別率變化較大。(2)在Yale人臉數據庫和ORL人臉數據庫和埃塞克斯大學人臉數據庫的實驗結果對比中可以看出Yale人臉數據庫的結果相對于ORL人臉數據庫和埃塞克斯大學人臉數據庫的實驗結果要差一些。根據Yale人臉數據庫中人臉圖像存在亮度變化,因此推斷GILTSA算法對于亮度的變化比較敏感,但是其真實性還需要其他存在亮度變化的人臉數據庫驗證。(3)在實驗中,根據經驗固定了近鄰數參數和局部流形維度,但是兩者之間大幅度變化對于結果的影響還沒有驗證。所以在接下來的工作中計劃:(1)驗證光照是否對于ILTSA算法結果影響過大;(2)近鄰數參數和局部流形維度的最佳選擇。

［1］ Jolliffe I.Principal Component Analysis［M］.［S.l.］: John Wiley&Sons,Ltd.,2005.

［2］ Comon P.Independent Component Analysis,a New Concept［J］.Signal Processing,1994,36(3):287-314.

［3］ Duda R O,Hart P E,Stork D G.Pattern Classification［M］.［S.l.］:John Wiley&Sons,Ltd.,2012.

［4］ Seung H S,Lee D D.The Manifold Ways of Perception［J］.Science,2000,290(5500):2268-2269.

［5］ Shashua A,Levin A,Avidan S.Manifold Pursuit:A New Approach to Appearance Based Recognition［C］// Proceedings of the 16th International Conference on Pattern Recognition.［S.l.］:IEEE Press,2002:590-594.

［6］ Wong E K,Chen M.A New Robust Algorithm for Video Text Extraction［J］.Pattern Recognition,2003,36 (6):1397-1406.

［7］ 朱明旱.基于流形學習的人臉表情識別研究［D］.長沙:中南大學,2009.

［8］ Tenenbaum J B,de Silva V,Langford J C.A Global Geometric Framework for Nonlinear Dimensionality Reduction［J］.Science,2000,290(5500):2319-2323.

［9］ Roweis S T,SaulL K.Nonlinear Dimensionality Reduction by Locally Linear Embedding［J］.Science, 2000,290(5500):2323-2326.

［10］ 譚 璐.高維數據的降維理論及應用［D］.長沙:國防科學技術大學,2005.

［11］ Belkin M,Niyogi P.Laplacian Eigenmaps for Dimensionality Reduction and Data Representation［J］.Neural Computation,2003,15(6):1373-1396.

［12］ Zhang Zhenyue,Zhang Hongyuan.Principal Manifolds and Nonlinear Dimension Reduction via Local Tangent Space Alignment［J］.SIAM Journal on Scientific Computing, 2002,26(1):313-338.

［13］ 王建忠.高維數據幾何結構及降維［M］.北京:高等教育出版社,2012.

［14］ Zhang Peng,Qiao Hong,Zhang Bo.An Improved Local Tangent Space Alignment Method for Manifold Learning［J］.Pattern Recognition Letters,2011,32(2):181-189.

［15］ Zhang Shiqing.Enhanced Supervised Locally Linear Embedding［J］.Pattern Recognition Letters,2009,30(13): 1208-1218.

［16］ He Xiaofei.Neighborhood Preserving Embedding［C］// Proceedings of the 10th IEEE International Conference on ComputerVision.［S.l.］:IEEE Press,2005: 1208-1213.

［17］ He Xiaofei,Niyogi P.Locality Preserving Projections［EB/OL］.(2004-12-23).http://people.cs.uchicago.edu/～xiaofei/LPP.html.

［18］ Zhang Tianhao,Yang Jie,Zhao Deli,et al.Linear Local TangentSpace Alignmentand Application to Face Recognition［J］.Neurocomputing,2007,70(7):1547-1553.

［19］ Li Hongyu,Li Teng,Chen Wenbin,et al.Supervised Learning on LocalTangentSpace［M］.Berlin, Germany:Springer,2005.

［20］ Yang Yi,Nie Feiping,Xiang Shiming,et al.Local and Global Regressive Mapping for Manifold Learning with Out-of-sample Extrapolation［C］//Proceedings of the 24th AAAI Conference on Artificial Intelligence and the 22nd Innovative Applications of Artificial Intelligence Conference.［S.l.］:American Association for Artificial Intelligence Press,2010:649-654.

編輯 任吉慧

Local Tangent Space Alignment Algorithm of Generalized Improvement

ZHAO Liaoying1,LI Fujie1,LI Xiaorun2
(1.Institute of Computer Application Technology,Hangzhou Dianzi University,Hangzhou 310018,China;
2.College of Electrical Engineering,Zhejiang University,Hangzhou 310027,China)

The Improved Local Tangent Space Alignment(ILTSA)can obtain better low dimension feature for face recognition because it can efficiently recover the problem that the Local Tangent Space Alignment(LISA)fails to reveal the manifold structure in the case when data are sparse or non-uniformly distribute or when the data manifold has large curvatures.To solve the problem that the ILTSA cannot efficiently handle ever-increasing data set,this paper presents a Generalization method for the ILTSA(GILTSA).The nearest neighborhood set is obtained based on the distance defined according to the classes of the samples,then the low manifold of the training set is implemented using the ILTSA.Through finding the nearest sample in the training set,and the low manifold of a new sample is approximately calculated by the projection of its nearest sample.Experimental results on the ORL,the Yale and the University of Essex face image database indicate that the proposed GILTSA method increases the overall accuracy compared with Principal Component Analysis(PCA)and Linear Local Tangent Space Alignment(LLTSA)algorithm etc.

manifold learning;Local Tangent Space Alignment(LTSA);generalization;feature extraction;face recognition

1000-3428(2014)11-0160-07

A

TP18

10.3969/j.issn.1000-3428.2014.11.032

國家自然科學基金資助項目(61171152);浙江省自然科學基金資助項目(LY13F020044)。

趙遼英(1970-),女,教授、博士,主研方向:模式識別,遙感圖像分析;李富杰,碩士研究生;厲小潤,研究員、博士。

2013-11-11

2013-12-13E-mail:690789991@qq.com

中文引用格式:趙遼英,李富杰,厲小潤.泛化改進的局部切空間排列算法［J］.計算機工程,2014,40(11):160-166.

英文引用格式:Zhao Liaoying,Li Fujie,Li Xiaorun.Local Tangent Space Alignment Algorithm of Generalized Improvement［J］.Computer Engineering,2014,40(11):160-166.