低重力模擬系統控制策略

朱齊丹，陳力恒，盧鴻謙

（1.哈爾濱工程大學自動化學院，黑龍江哈爾濱150001；2.哈爾濱工業大學控制理論與制導技術研究中心，黑龍江哈爾濱150001）

低重力模擬系統控制策略

朱齊丹1，陳力恒1，盧鴻謙2

（1.哈爾濱工程大學自動化學院，黑龍江哈爾濱150001；2.哈爾濱工業大學控制理論與制導技術研究中心，黑龍江哈爾濱150001）

為了使低重力模擬系統滿足月球巡視車研發、調試的要求，系統需克服傳統方法在豎直方向出現擾動時，抑制效果不好的問題，為此搭建了提供豎直方向拉力的恒張力伺服子系統。在分析關鍵部件工作特性的基礎上，建立了范數有界參數不確定性控制對象模型，分離了標稱模型與不確定性參數。根據系統的特點和巡視車測試過程中對于低重力環境的指標需求，針對性的設計了H∞控制器。通過仿真檢驗，控制器抑制了系統參數不確定的影響，避免了電機的機械諧振發生，并且在巡視車豎直方向加速度干擾的情況下，保證系統最大誤差僅為3.4 N。

魯棒控制；參數不確定；恒張力；低重力模擬系統；月球巡視車；控制策略

隨著我國“嫦娥”探月工程的深入進行，利用巡視車對月球表面勘察、采樣成為了未來的一項重要任務。為了保證巡視車動力性能可以適應月球的低重力場，需要在發射前模擬低重力環境對巡視車進行檢測、調試，否則不匹配的動力性可能會破壞巡視車設備［1］，對勘探任務造成巨大影響。

在各類低重力模擬系統中，普遍存在面對豎直方向大幅擾動時，系統魯棒性變差，甚至無法維持低重力環境的問題。例如利用氣浮平臺產生氣體浮力抵消重力的方法，但該方法主要適用于飛行器的水平面內微重力實驗［2-3］，對于巡視車實際工作時大幅顛簸無法做出性能評價。利用水中浮力與重力平衡的方法雖然可以理論上解決這一問題［4-5］，但對于巡視車防水密封性提出很高的要求，大大增加了巡視車的制造成本與難度。因此通過吊索將巡視車吊起的“懸吊法”被提出，使低重力模擬系統在機械結構上易于實現［6-7］，但由于系統缺少主動控制，面對豎直方向擾動時的抑制效果不好。所以在“懸吊法”的基礎上加入雙電機結構的“主動懸吊法”被提出［8-9］，然而雙電機使得機械諧振點過多，導致系統帶寬過窄滿足不了巡視車實際測試需要；并且沒有考慮系統關鍵參數等效彈性系數的不確定性變化，這會導致在實際工作中系統的魯棒穩定性變差。

針對上述問題，本文在“懸吊法”的基本原理上改用單電機結構與彈簧協同工作，設計了在抑制擾動方面具有強魯棒性優勢的H∞控制器，通過仿真檢驗，系統工作狀態平穩，控制精度滿足了巡視車性能測試要求。

1 系統模型的建立

1.1 控制對象模型的建立

低重力模擬系統提供豎直方向拉力的恒張力子系統主要由彈簧、電機、減速器、抱閘、滾筒、擺桿、滑輪、拉力傳感器等部分組成，其結構框圖如圖1。

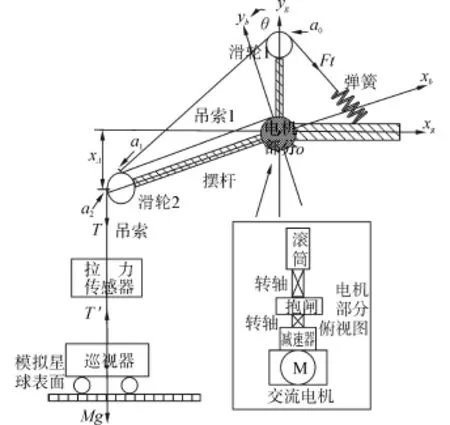
圖1 恒張力子系統結構框圖Fig.1 The structure diagram of the constant tension subsystem

圖1 中設吊索對巡視車拉力為T＇，巡視車地球表面所受重力為Mg，在模擬低重力環境中巡視車所受重力為Gc：

將滑輪2與擺桿視為等效擺桿，設吊索對等效擺桿的拉力為T，向上為正方向，則

由式（1）、（2）知：對Gc的控制可等價為對T的控制問題。

圖1中當巡視車處于平衡狀態即θ＝0時，緩沖機構利用彈簧拉伸為巡視車平衡工作點提供拉力，此時吊索對等效擺桿拉力為T0。當巡視車工作在上下顛簸的路面時，首先在電機做出反應之前，彈簧帶動擺桿的擺動先抵消巡視車的部分擾動，以避免吊索張力迅速變化使得低重力系統動態誤差不滿足巡視車測試要求；拉力傳感器測得T后與T0比較，通過控制器給電機下達指令，電機利用收放繩索補償巡視車豎直方向位置偏移導致的T變化，使T能夠穩定在T0附近，且動態誤差盡量小以減少對巡視車性能測試結果的影響。

圖1中彈簧張力為Ft，彈簧彈性系數為k，等效擺桿末端距離水平位置的偏移距離為xΔ，等效擺桿長度為l，等效擺桿轉動慣量為J，等效擺桿工作時擺動角度為θ。在重力坐標系xgoyg中設＝等效擺桿拉力在重力坐標系為0 T[]T；擺桿坐標xboyb到xgoyg旋轉矩陣為：根據胡克定律：

設吊索1對a1點拉力為，則＝，設向上為正方向，根據剛體定軸轉動定律，對擺桿建立動力學方程：

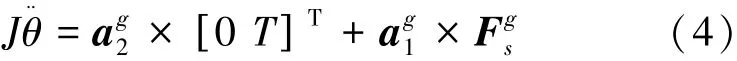
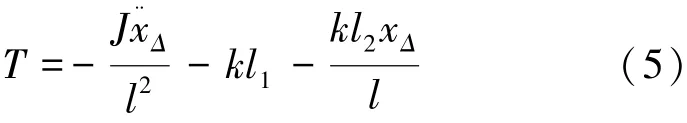
則在平衡位置θ＝0時

設ΔT為系統工作時T距T0變化量，則

在式（5）中令等效彈性系數和等效質量分別為

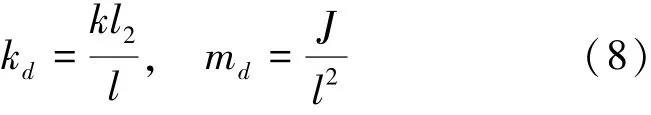
將式（6）～（8）代入式（5），得

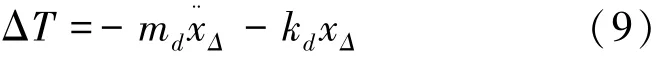
因此使T能夠穩定在T0，且動態誤差盡量小的控制目標可等價為：使ΔT穩定在0，且動態誤差盡量小。

設xd為巡視車豎直方向的位移量，xu為電機收放吊索的位移量，l＇平衡狀態下等效擺桿末端到巡視車的吊索長度，由圖1吊索長度建立等式：整理可得：

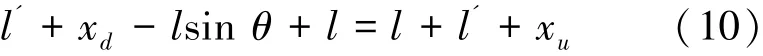
設電機對吊索收放速度為x·u，滾筒半徑為r，為了方便電機對吊索進行位置控制，將交流力矩電機直驅系統工作調節在速率模式。可通過實驗利用基于頻率響應的模型參數辨識法，獲得交流力矩電機從u到x·u的等效控制傳遞函數［9］：

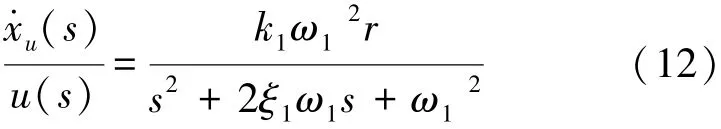
為了方便后續的控制器設計，采用機理建模獲取控制對象狀態空間表達式，取x1＝xu，x2＝xu，x3＝x¨u，x4＝xd，x5＝xd，d＝x¨d，y＝ΔT，聯立式（9）、（11）、（12），得：

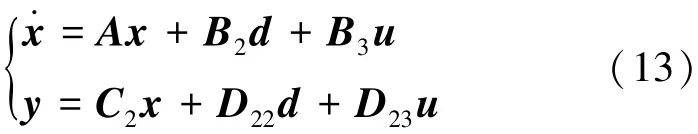
其中：

1.2 含參數不確定性控制對象模型的建立

將k＝3 500 N／m，l1＝0.22 m，l2＝0.1 m，l＝0.23 m，J＝0.45 kg·m2代入式（8），可以得到kd＝1 552 N／m，md＝8.5 kg，實際系統中md的變化可忽略，而kd會產生ω0＝5%的波動，取巡視車加速度幅值為0.7 m／s2，頻率為5 Hz時，拉力誤差如圖2。

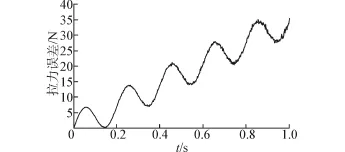
圖2 開環拉力誤差Fig.2 Tension error in the open loop

可見巡視車豎直方向加速度及不確定性對控制吊索拉力恒定帶來很大困難，為使控制器克服系統含有的參數不確定性，需建立含參數不確定的控制模型。

建立含參數不確定性控制模型主要有建立多面體系統和建立范數有界參數不確定系統2種方法。多面體系統對于參數分析是一種很好的途徑，然而在控制設計上并沒有好的方法［10］。而范數有界模型處理方法則可以有效的與控制器設計結合，因此采用范數有界模型處理參數不確定性。

其中：

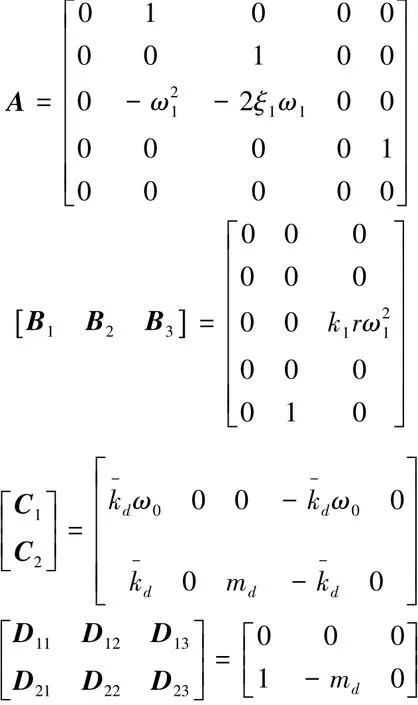
為了方便分析式（14）可用圖3來表示，通過引入輸入項ω與輸出項z1，將不確定部分與系統標稱模型分離，使得控制器在對系統性能做出改善的同時可以對不確定參數變化時的系統響應的變化做出抑制。將各參數數值0.1 m，ξ1＝0.3，kd＝1 552 N／m，md＝8.5 kg代入式（14），并將系統化為最小實現：

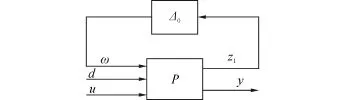
圖3 含范數有界參數不確定性控制對象模型Fig.3 The controlled object model of norm bounded parameter uncertainty

2 控制器策略的選擇與設計

2.1 控制策略的選擇

針對系統面臨的巡視車豎直方向加速度的干擾，電機部分機械諧振問題，緩沖機構參數不確定，控制策略選擇上需以結合系統不確定性和外部擾動的抑制為重點確定控制器類型。

H∞控制是近年來在工業實際中應用較廣的一種控制策略［11］，它可以將外部擾動與本身模型的不確定性轉化為同一形式，并通過傳遞函數Hωz（s）將其被調輸出的H∞范數最小為基本思想，使得在抑制擾動及不確定性問題上擁有很好的效果；H∞控制器在求解過程中利用小增益定理保證閉環系統的穩定性，因此通過H∞控制器綜合出的系統往往具有良好的魯棒穩定性，所以H∞控制成為了低重力模擬系統控制器設計的首選。并且Matlab軟件為H∞控制提供了專門的函數，使得控制器在求解過程中，擺脫了繁雜的公式計算，簡化了控制器的設計。

2.2 H∞控制器的設計

將控制系統實現框圖如圖4轉化為H∞控制的標準結構如圖5所示，K為待求的控制器，z為待設計的系統被調輸出，P為系統廣義控制對象，P由系統標稱模型和加權函數組成，首先設計它的結構框圖如圖6，根據系統存在抑制參數不確定性、電機的高頻諧振及外部干擾上的性能需求，選取了被調輸出：z1為不確定性輸出，z2為控制電壓的被調輸出，z3為吊索拉力變化的被調輸出；相應的加權函數上選取：wd為干擾的加權函數，wu為對控制輸入的加權函數，wf為吊索張力變化加權函數。加權函數的選取將直接決定系統能否滿足月球巡視車測試時的要求。

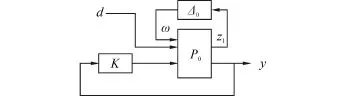
圖4 控制系統實現框圖Fig.4 The block diagram of control system

圖5 H∞控制結標準結構Fig.5 The standard structure of the H∞controller

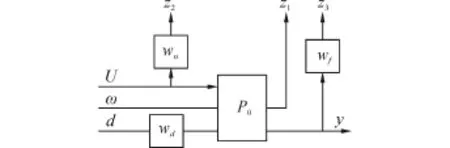
圖6 恒張力伺服系統廣義控制對象PFig.6 The generalized control object P of the constant tension servo system

加權函數wd用來模擬干擾的輸入，為了使控制器能抑制干擾最嚴重的情況，wd取巡視車工作時豎直方向加速度幅值最大值，即wd＝0.7。

加權函數wf作用是在巡視車豎直方向加速度頻率段內即f≤5 Hz，懲罰巡視車干擾對吊索拉力變化量影響，使得d到y的幅頻特性在f≤5 Hz盡量小，而對工作頻段外幅頻特性可能的升高不做限制，因此設計wf為低通濾波器形狀傳遞函數：wf＝

加權函數wu用來懲罰控制輸入u的高頻信號，以避免執行機構發生飽和，而對u的低頻信號不做限制，因此wu設計為高通濾波器形狀的傳遞函數，結合系統帶寬可實現性及機械諧振頻率點，將其轉折頻率設置為100 rad／s。為了保證盡量保證H∞最優指標γ≤1，以確保綜合出的控制器使系統滿足小增益定理［10］保證系統的魯棒穩定，對wu的增益進行調試，確定

利用Matlab提供的hinflmi函數，可以通過編程求得此時H∞最優指標γ＝0.935 4，滿足小增益定理，控制器K的Bode圖如圖7。

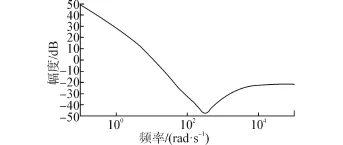
圖7 控制器K的Bode圖Fig.7 The Bode diagram of the controller K

由圖7知，控制器在低頻段增益較大，以抑制巡視車工作時帶來的干擾。在300 rad／s附近出現明顯的陷波特性，與電機諧振峰值處頻率相近，與限制控制器帶寬方法結合，共同抑制機械諧振對系統的影響。控制器帶寬與文獻［9］相比，得到了明顯增大，減少了控制器的保守性。

為了檢驗系統魯棒穩定性，利用wcgain函數得到不確定參數對閉環系統影響最嚴重時的參數值kd＝1 629.6 N／m，并將其代入閉環系統狀態矩陣A＇中，計算A＇特征值為

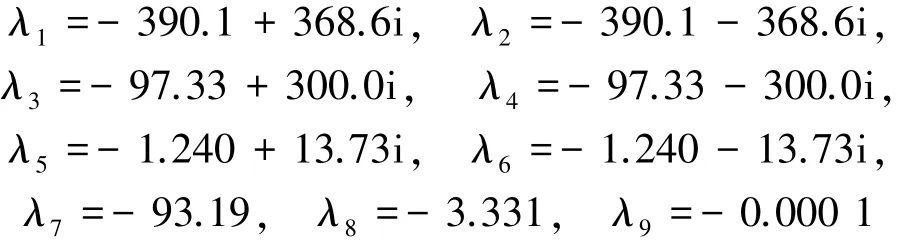
因此可驗證控制器使得系統魯棒穩定。

3 控制器魯棒性仿真檢驗

巡視車豎直方向加速度模型可表示為x¨d＝ Asin（2πft），其中｜A｜≤0.7 ms2，頻率f≤5 Hz。為了保證巡視車性能測試時的準確性，要求低重力模擬系統的動態誤差｜ΔT｜在5 N以內。在Matlab軟件里為了檢驗系統在實際工作中的魯棒性，仿真中加入模擬拉力傳感器的噪聲模塊，傳感器采樣頻率600 Hz，方差為0.01N2。取干擾最嚴重的情況，即A＝0.7m／s2，f＝5 Hz，仿真時間為10 s，仿真結果如圖8所示。

圖8表明在干擾最嚴重情況下所設計的控制器使系統保持穩定。在圖8（a）中｜ΔT｜≤3.4 N，控制精度得到了很好的保證。圖8（b）表明面對高頻擾動時，電機的輸入電壓不足0.8 V，而電機的工作電壓范圍為－10～＋10 V，因此干擾對于電機工作負擔很輕，減輕了電機的磨損。圖8（c）在干擾頻率最高時，繩索收放速度最大為0.05 m／s，電機輸出未出現幅值“堵塞”現象，表明電機可以跟上巡視車對系統的擾動。

由圖9對比可知，對于不確定性Δ的變動，系統保持穩定，且ΔT變化幾乎沒有受到影響，表明控制器很好地抑制了不確定性參數變化對系統的影響，因此系統具有良好的魯棒性。

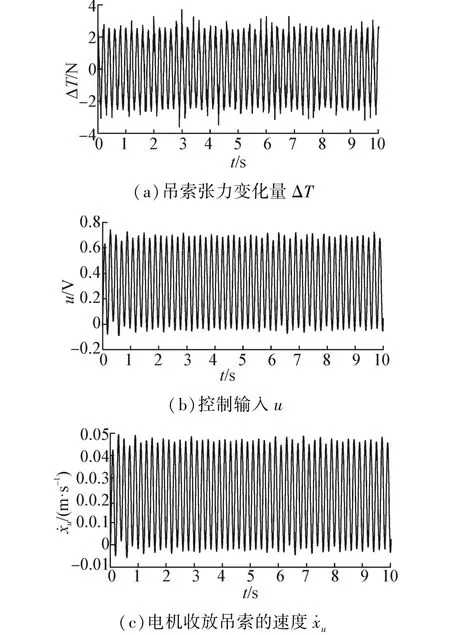
圖8 干擾最嚴重時系統關鍵信號的響應Fig.8 The key signal responses of the height interference

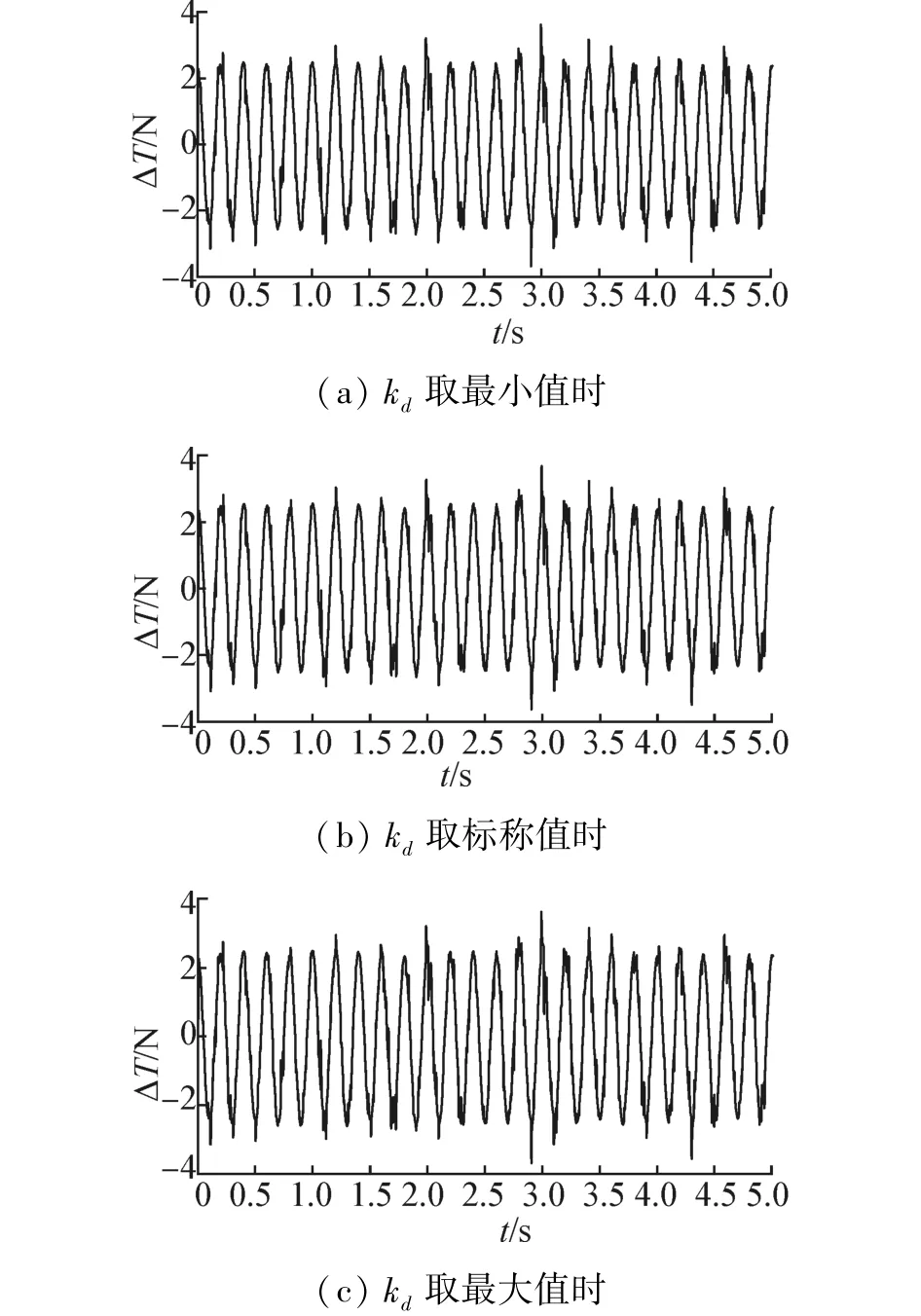
圖9 kd的變動時吊索拉力變化Fig.9 The sling tension changes when kdchanges

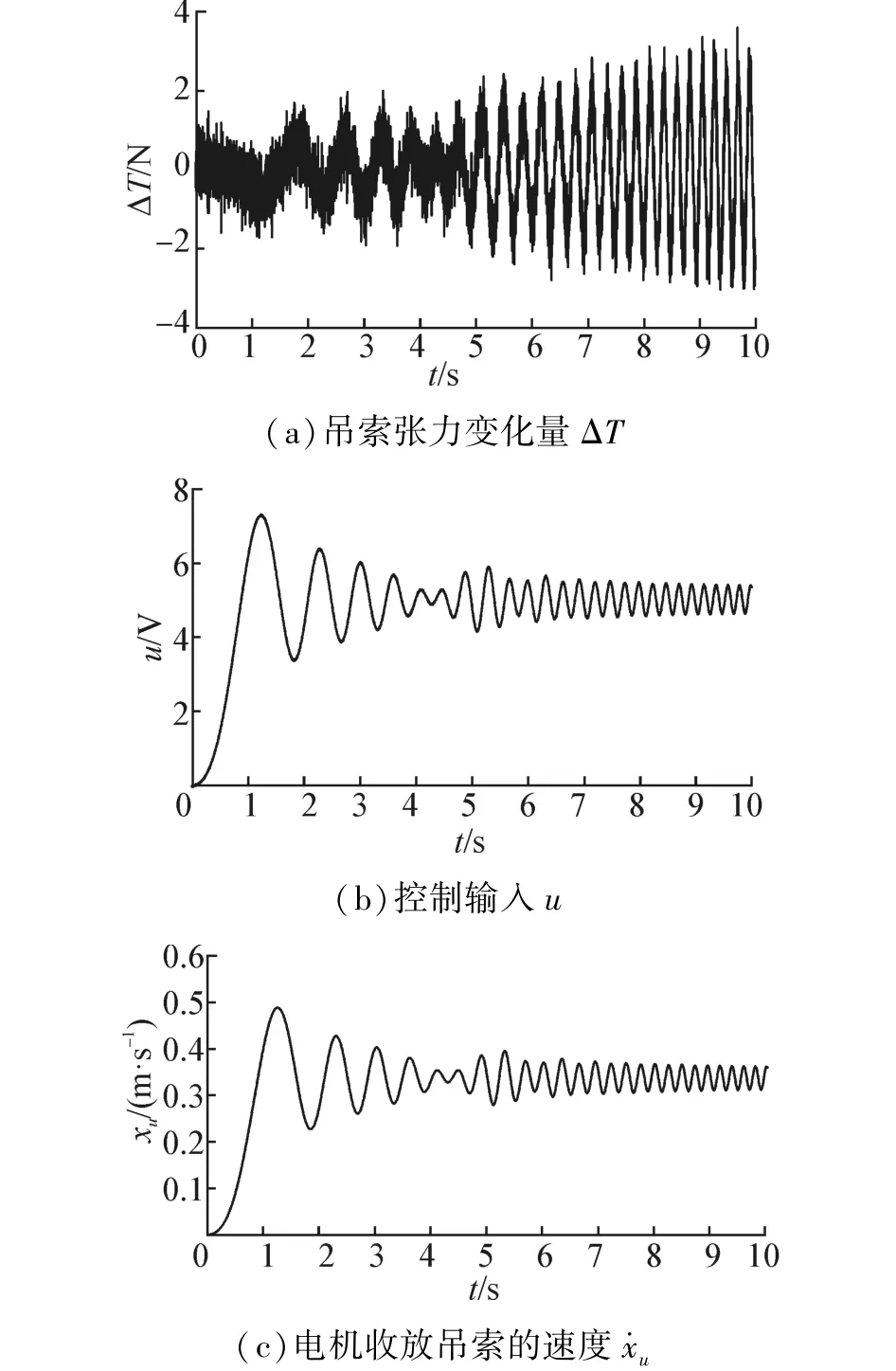
圖10 掃頻模式下系統關鍵信號響應Fig.10 The key signal system response in the frequency sweep mode

取巡視車工作在指標A＝0.7 m／s2時，對系統掃頻，頻率范圍為巡視車工作時豎直方向加速度頻率變化范圍0.1～5 Hz，仿真時間10 s。由圖10（a）可知，在巡視車工作的加速度頻率范圍內，吊索拉力最大動態誤差為3.4 N，滿足了巡視車測試對與低重力模擬系統的要求。由圖10（b）可知，控制電壓在各頻率段處于工作電壓范圍內，保證了電機正常工作，并且輸入電壓在高頻段變小，驗證了彈簧吸收巡視車的高頻擾動的作用，減輕電機在高頻段的工作壓力。

4 結束語

對于傳統低重力模擬方式在面對巡視車豎直方向大幅顛簸時，低重力效果差、精度變低、不穩定的問題。本文針對性的建立了控制對象模型，并實現了參數不確定問題的分離；對于帶寬有限及干擾抑制的要求，設計了具有強魯棒性優勢的H∞控制器；在仿真檢驗中，控制器不僅抑制了巡視車豎直方向大幅度顛簸對于穩定性以及精度的影響，并且保證了參數不確定性下的系統魯棒性；通過對于控制輸入的監控，該控制器可以確保系統的可實現性；在掃頻模擬巡視車加速度干擾的條件下，系統的最大誤差不超過3.4 N。

由于本文沒有考慮系統內部存在的摩擦，吊索諧振等因素，使得實際物體和理論模型仍然存在差別，未來可以結合上述因素對控制器進行進一步的完善，并在實驗條件允許下搭建實際系統，可以為月球巡視車的性能調試提供更大的幫助。

［1］肖福根，葉培建.月球探測工程中的月球環境問題［J］.航天器環境工程，2006，23（1）：1-3.XIAO Fugen，YE Peijian.Issues about lunar environment in lunar exploration project［J］.Spacecraft Environment Engineering，2006，23（1）：1-3.

［2］齊乃明，張文輝，高九州，等.空間微重力環境地面模擬試驗方法綜述［J］.航天控制，2011，29（3）：95-100.QI Naiming，ZHANG Wenhui，GAO Jiuzhou，et al.The primary discussion for the ground simulation system of spatial microgravity［J］.Airspace Control，2011，29（3）：95-100.

［3］ISOBE T，NAGASAKA K，YAMAMOTO S.A new approach to kinematic control of simple manipulators［J］.IEEE Transactions on Systems，Man and Cybernetics，1992，22（5）：1116-1124.

［4］姚燕生，梅濤.空間操作的地面模擬方法-水浮法［J］.機械工程學報，2008，44（3）：182-188.YAO Yansheng，MEI Tao.Simulation method of space operation on the ground-buoyancy method［J］.Chinese Journal of Mechanical Engineering，2008，44（3）：182-188.

［5］姚燕生.三維重力補償方法與空間浮游目標模擬實驗裝置研究［D］.合肥：中國科學技術大學，2006：56-80.YAO Yansheng.Research on 3-D gravity compensation and equipment of space floating objective simulation［D］.Hefei：U-niversity of Science and Technology of China，2006：56-80

［6］SATO Y，EJIRI A，IIDA Y，et al.Micro-G emulation system using constant-tension suspension for a space manipulator［C］／／Robotics and Automation，1991.Sacramento，America，1991：1893-1900.

［7］WHITE G，XU Y.An active vertical-direction gravity compensation system［J］.IEEE Transactions on Instrumentation and Measurement，1994，43（6）：786-792.

［8］王連明.低重力模擬系統控制算法的研究［D］.哈爾濱：哈爾濱工業大學，2010：10-30.WANG Lianming.Research on control algorithm of microgravity simulating system［D］.Harbin：Harbin Institute of Technology，2010：10-30.

［9］王樂.低重力模擬器吊索張力控制算法研究［D］.哈爾濱：哈爾濱工業大學，2011：11-20.WANG Le.Control algorithm on the sling tension of low-gravity simulating system［D］.Harbin：Harbin Institute of Technology，2011：11-20.

［10］劉志康，姚郁.線性魯棒控制［M］.北京：科學出版社，2013：277-300.

［11］俞立.魯棒控制-線性矩陣不等式處理方法［M］.北京：清華大學出版社，2002：44-59.

The control strategy of low gravity simulation system

ZHU Qidan1，CHEN Liheng1，LU Hongqian2
（1.College of Automation，Harbin Engineering University，Harbin 150001，China；2.Center for Control Theory and Guidance Technology，Harbin Institute of Technology，Harbin 150001，China）

In order to make the low gravity simulation system meet the research and debugging of a lunar rover，the system needs to overcome the problem that the system cannot work well when the disturbance is in vertical direction.A constant tension servo system for providing vertical tension is set up.The working characteristics of key components are analyzed and the mathematical model of the key components is established，which includes the normbounded parameter uncertainty.The nominal model and the uncertainty parameter were separated.According to the characteristics of the system and the index requirements of the lunar rover testing process for low gravity environment，the H∞controller of the system is designed for this purpose.It is verified that the controller solves the problem of the parameter uncertainty and avoids the mechanical resonance of the motor.The system ensured that the error is less than 3.4 N under the interference of the vertical acceleration of the lunar rover.

robust controller；parameter uncertainty；constant tension；low gravity simulation；lunar rover；control strategy

10.3969／j.issn.1006-7043.201309039

http：／／www.cnki.net／kcms／detail／23.1390.U.20140925.1517.001.html

TP273

A

1006-7043（2014）11-1384-06

2013-09-11.網絡出版時間：2014-09-25.

國家自然科學基金資助項目（61175089，61203255，61021002）.

朱齊丹（1963-），男，教授，博士生導師.

朱齊丹，E-mail：zhuqidan＠hrbeu.edu.cn.