基于Ansoft軟件的牽引用直線感應(yīng)電機(jī)的有限元分析＊

李 霄 陶彩霞

（蘭州交通大學(xué)自動(dòng)化與電氣工程學(xué)院，730070，蘭州∥第一作者，碩士研究生）

城市的發(fā)展對(duì)新建城市軌道交通線路的制約條件越來(lái)越多，人們對(duì)軌道交通的要求也越來(lái)越高。直線感應(yīng)電機(jī)軌道系統(tǒng)比傳統(tǒng)感應(yīng)電機(jī)軌道交通系統(tǒng)擁有更小的曲線半徑、更強(qiáng)的爬坡能力，易在復(fù)雜的城市環(huán)境中運(yùn)行，已成為多種城市軌道交通系統(tǒng)中的一員。廣州地鐵4號(hào)線、5號(hào)線和6號(hào)線，以及北京軌道交通首都國(guó)際機(jī)場(chǎng)線，都選擇了這種城市軌道交通系統(tǒng)。然而，對(duì)于直線感應(yīng)電機(jī)而言，存在道岔處感應(yīng)板不連續(xù)、氣隙值大、邊端效應(yīng)等問(wèn)題［1－3］。本文利用 Ansoft軟件的 Transient模塊，采用有限元方法對(duì)直線感應(yīng)電機(jī)在起動(dòng)、穩(wěn)態(tài)運(yùn)行及經(jīng)過(guò)道岔處的動(dòng)態(tài)性能進(jìn)行了分析。

1 牽引用直線感應(yīng)電機(jī)的原理及特性

軌道交通一般采用短初級(jí)、復(fù)合感應(yīng)板的單邊型直線感應(yīng)電機(jī)，其工作原理與旋轉(zhuǎn)感應(yīng)電機(jī)相同（如圖1所示）。初級(jí)繞組被安裝在列車底部，次級(jí)感應(yīng)板鋪設(shè)在軌道中心。由于初級(jí)繞組的開斷，形成了兩個(gè)邊端。為了確保運(yùn)行的安全，初級(jí)與次級(jí)感應(yīng)極之間的間隙遠(yuǎn)遠(yuǎn)大于旋轉(zhuǎn)電動(dòng)機(jī)的氣隙，因此體現(xiàn)出了多種特性。

圖1 短初級(jí)單邊型直線感應(yīng)電機(jī)

直線感應(yīng)電機(jī)不同于旋轉(zhuǎn)感應(yīng)電機(jī)的最大特點(diǎn)就是存在邊端效應(yīng)。邊端效應(yīng)可分為靜態(tài)橫向邊端效應(yīng)、動(dòng)態(tài)橫向邊端效應(yīng)、靜態(tài)縱向邊端效應(yīng)和動(dòng)態(tài)縱向邊端效應(yīng)。在直線感應(yīng)電機(jī)軌道交通系統(tǒng)中，靜態(tài)橫向邊端效應(yīng)的本質(zhì)是空載氣隙磁場(chǎng)的橫向擴(kuò)散。當(dāng)初級(jí)鐵心疊片厚度小于次級(jí)感應(yīng)板寬度時(shí)，這種效應(yīng)對(duì)電機(jī)的影響往往可以忽略。動(dòng)態(tài)橫向邊端效應(yīng)與次級(jí)感應(yīng)板橫向超出初級(jí)繞組的長(zhǎng)度和極距的比值相關(guān)：比值越大，動(dòng)態(tài)橫向邊端效應(yīng)對(duì)電機(jī)的影響就越小。通常比值大于0.4時(shí)，動(dòng)態(tài)橫向邊端效應(yīng)的影響會(huì)極大地削弱。增加電機(jī)的極數(shù)會(huì)減小互感之間的不對(duì)稱。當(dāng)極數(shù)增加到6以上時(shí)動(dòng)態(tài)橫向邊端效應(yīng)的影響可以忽略。縱向動(dòng)態(tài)邊端效應(yīng)對(duì)牽引用直線感應(yīng)電機(jī)的影響最大，需對(duì)其電磁特性進(jìn)行分析，并在電機(jī)的設(shè)計(jì)和控制上進(jìn)行完善。縱向動(dòng)態(tài)邊端效應(yīng)所帶來(lái)的影響是牽引用直線感應(yīng)電機(jī)要解決的主要問(wèn)題之一［1］。

2 直線感應(yīng)電機(jī)的磁場(chǎng)基本方程

直線感應(yīng)電機(jī)因其特有的邊端效應(yīng)，需利用麥克斯韋方程組計(jì)算其特性。麥克斯韋方程組需要作一些修改才能應(yīng)用于直線感應(yīng)電機(jī)。因?yàn)樵诮蛔兇艌?chǎng)中導(dǎo)電媒質(zhì)除因磁場(chǎng)隨時(shí)間發(fā)生變化而產(chǎn)生感應(yīng)電場(chǎng)外，還因磁場(chǎng)與導(dǎo)電媒質(zhì)之間的相對(duì)運(yùn)動(dòng)而產(chǎn)生的速度電場(chǎng)。這兩種電場(chǎng)在導(dǎo)電媒質(zhì)中共同引起了感應(yīng)電流。另外，直線感應(yīng)電機(jī)的激勵(lì)頻率較低，所以位移電流可以忽略不計(jì)［4］。經(jīng)過(guò)修改后，用于直線感應(yīng)電機(jī)的基本電磁場(chǎng)方程為：

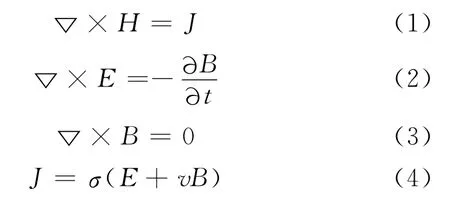
式中：

H——磁場(chǎng)強(qiáng)度；

E——電場(chǎng)強(qiáng)度；

B——磁感應(yīng)強(qiáng)度（磁通密度）；

J——電流密度；

σ——電導(dǎo)率；

t——時(shí)間；

v——電荷在磁場(chǎng)中的運(yùn)動(dòng)速度。

為了估算磁場(chǎng)作用下所產(chǎn)生的力F，采用麥克斯韋應(yīng)力張量是一種有效的方法。式（5）通過(guò)對(duì)一個(gè)包含初級(jí)繞組的封閉曲面進(jìn)行面積分，來(lái)估算F

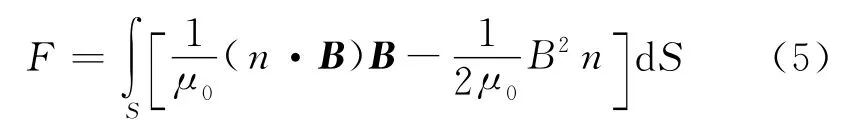
式中：

n——封閉曲面上的單位法向量；

B——磁感應(yīng)強(qiáng)度矢量；

S——封閉曲面的面積。

那么磁場(chǎng)產(chǎn)生的推力和垂向力分別是力F的x和y向的分量，可分別表示為：

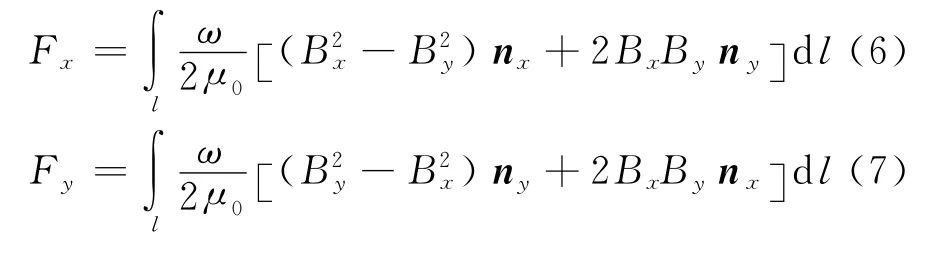
式中：

Bx——磁感應(yīng)強(qiáng)度的x向分量；

By——磁感應(yīng)強(qiáng)度的y向分量；

nx——封閉曲面上x向的單位正交矢量；

ny——封閉曲面上y向的單位正交矢量；

μ0——真空磁導(dǎo)率；

ω——初級(jí)鐵心的寬度；

l——在二維分析中的圍繞初級(jí)繞組區(qū)域的一條閉合線［5］。

3 牽引用直線感應(yīng)電機(jī)的有限元仿真分析

3.1 有限元分析模型

通過(guò)Ansoft Maxwell 2D軟件的Transient求解器，采用運(yùn)動(dòng)表面算法對(duì)做平移運(yùn)動(dòng)的直線感應(yīng)電機(jī)進(jìn)行瞬態(tài)仿真。忽略直線感應(yīng)電機(jī)的橫向邊端效應(yīng)，考慮道岔處感應(yīng)板不連續(xù)的情況，對(duì)牽引用直線感應(yīng)電機(jī)進(jìn)行建模。電機(jī)主要參數(shù)見表1。

表1 牽引用直線感應(yīng)電機(jī)主要參數(shù)表［6］

建模過(guò)程主要分為：生成幾何模型，選定材料，設(shè)定激勵(lì)源和邊界條件，定義執(zhí)行參數(shù)和定義求解選項(xiàng)［7］。其中，定義求解選項(xiàng)時(shí)需設(shè)置一個(gè)運(yùn)動(dòng)區(qū)域。該區(qū)域?qū)⑦\(yùn)動(dòng)的初級(jí)繞組和靜止不動(dòng)的次級(jí)感應(yīng)板分開，做平移運(yùn)動(dòng)的初級(jí)繞組必須始終在運(yùn)動(dòng)區(qū)域中，并按照時(shí)間步長(zhǎng)和速度值的設(shè)定做時(shí)步位移運(yùn)動(dòng)。為了使初級(jí)繞組在模擬運(yùn)動(dòng)中有足夠的運(yùn)動(dòng)空間，運(yùn)動(dòng)區(qū)域要設(shè)置得足夠長(zhǎng)。物理模型如圖2所示。對(duì)模型的氣隙部分進(jìn)行了細(xì)致剖分，以得到磁場(chǎng)產(chǎn)生的推力、垂向力和氣隙磁場(chǎng)的精確計(jì)算結(jié)果。網(wǎng)絡(luò)剖分如圖3所示。

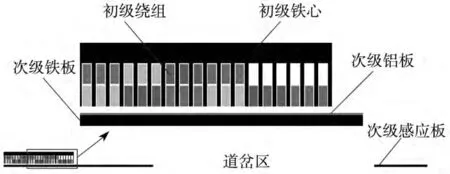
圖2 直線感應(yīng)電機(jī)物理模型圖

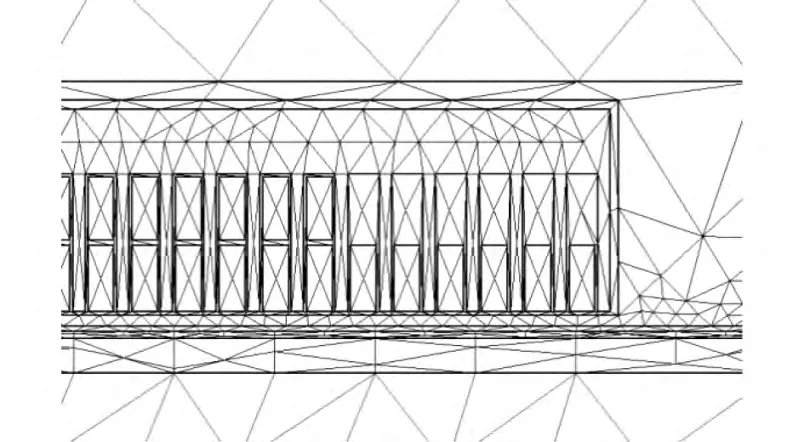
圖3 直線感應(yīng)電機(jī)網(wǎng)絡(luò)剖分圖

3.2 動(dòng)態(tài)性能分析

采用二維時(shí)步有限元分析法，通過(guò)后處理可以得到磁場(chǎng)產(chǎn)生的推力、垂向力、速度、位移及氣隙中的磁通分布曲線［8］。

當(dāng)直線感應(yīng)電機(jī)空載運(yùn)行、初速度為零、t＝0.01s時(shí)，磁力線分布如圖4所示。從圖中可以看出，磁通線由電機(jī)軛、電機(jī)齒進(jìn)入空氣隙后穿入次級(jí)感應(yīng)板；再?gòu)牧硪粋€(gè)電機(jī)齒進(jìn)入電機(jī)軛，形成一個(gè)極的閉合磁通線。由于電機(jī)兩端存在半填充槽，利用率低，從而產(chǎn)生漏磁通。如圖4所示電機(jī)含有6個(gè)極，其中5個(gè)完整的極和1個(gè)兩端分開的極，兩端磁通線通過(guò)空氣閉合［9］。

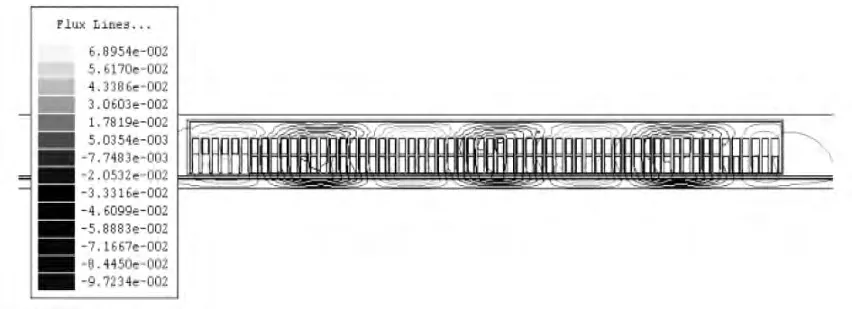
圖4 直線感應(yīng)電機(jī)磁力線分布仿真圖（t＝0.01s）

圖5～圖8為不同時(shí)刻直線感應(yīng)電機(jī)運(yùn)行位置與氣隙磁場(chǎng)密度分布圖。t＝1.1s時(shí)，電機(jī)運(yùn)行至圖5－a）所示的位置，初級(jí)繞組的入端部分已和次級(jí)感應(yīng)板脫離；此時(shí)氣隙磁場(chǎng)密度分布如圖5－b）所示，入端無(wú)次級(jí)感應(yīng)板區(qū)域的氣隙磁場(chǎng)分布相對(duì)平緩，沒(méi)有電機(jī)極的體現(xiàn)，相當(dāng)于電機(jī)極數(shù)減少，牽引能力隨之減弱。t＝1.5s時(shí)，電機(jī)運(yùn)行至圖6－a）所示的位置，初級(jí)繞組和次級(jí)感應(yīng)板完全脫離，氣隙磁場(chǎng)密度分布如圖6－b）所示；兩者的電磁感應(yīng)作用消失，磁通密度集中分布在同一區(qū)域。t＝2s時(shí)，電機(jī)運(yùn)行至圖7－a）所示的位置，初級(jí)繞組的入端部分駛出道岔，重新和次級(jí)感應(yīng)板作用；此時(shí)氣隙磁場(chǎng)密度分布如圖7－b）所示，隨著電機(jī)的繼續(xù)運(yùn)行，相當(dāng)于極數(shù)隨之增加，電機(jī)逐漸恢復(fù)正常運(yùn)行狀態(tài)。t＝2.3s時(shí)，電機(jī)運(yùn)行至圖8－a）所示的位置，次級(jí)感應(yīng)板完全覆蓋初級(jí)繞組；此時(shí)氣隙磁場(chǎng)密度分布如圖8－b）所示，可明顯看到縱向邊端效應(yīng)的影響，而入端氣隙磁場(chǎng)密度小于出端氣隙磁場(chǎng)密度。

圖9為直線感應(yīng)電機(jī)的推力隨時(shí)間變化的曲線。當(dāng)電機(jī)為空載運(yùn)行時(shí)，推力在初期處于震蕩狀態(tài)，0.52s后轉(zhuǎn)為穩(wěn)態(tài)，實(shí)際推力方向與軟件中定義的推力方向相同，因此推力為正值；在0.78s后電機(jī)運(yùn)動(dòng)到感應(yīng)板的邊緣位置，進(jìn)入無(wú)感應(yīng)板的道岔區(qū)域，推力開始下降直到為零；當(dāng)電機(jī)移出道岔重新和感應(yīng)板相作用時(shí)，推力開始回升至穩(wěn)態(tài)。圖10為直線感應(yīng)電機(jī)的垂向力隨時(shí)間變化的曲線，其變化規(guī)律同推力曲線大致相同。穩(wěn)態(tài)的垂向力為正值，表現(xiàn)為吸引力。當(dāng)電機(jī)在道岔區(qū)域時(shí)垂向力為零，吸力消失，影響電機(jī)的穩(wěn)定運(yùn)行。

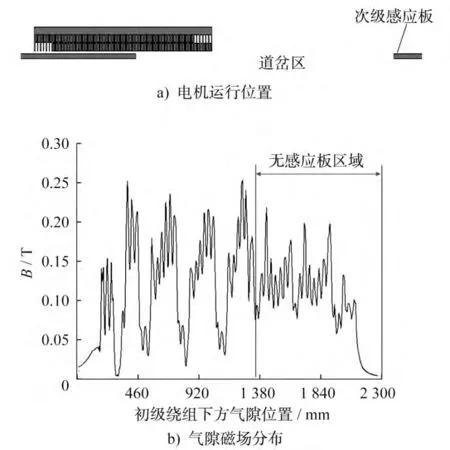
圖5 直線感應(yīng)電機(jī)運(yùn)行位置與氣隙磁場(chǎng)分布圖（t＝1.1s）

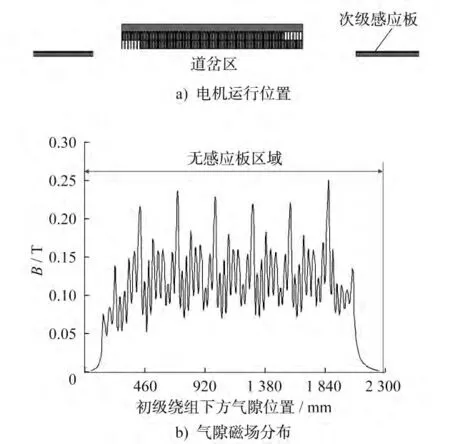
圖6 直線感應(yīng)電機(jī)運(yùn)行位置與氣隙磁場(chǎng)分布圖（t＝1.5s）

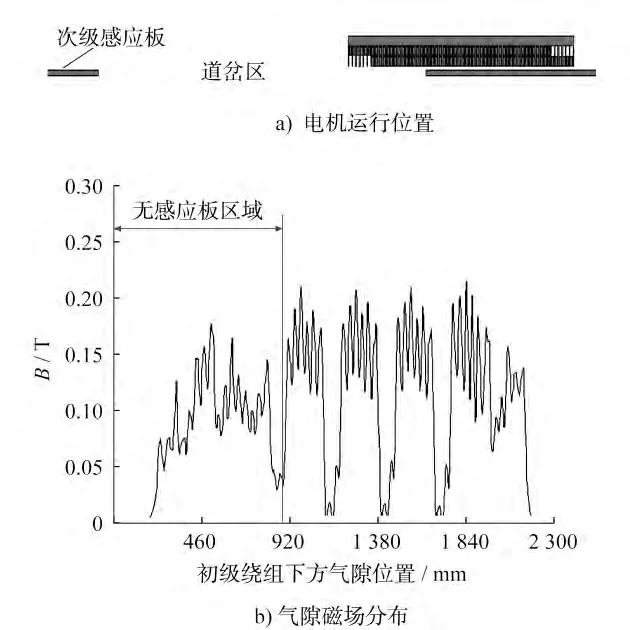
圖7 電機(jī)運(yùn)行位置與氣隙磁場(chǎng)分布圖（t＝2s）

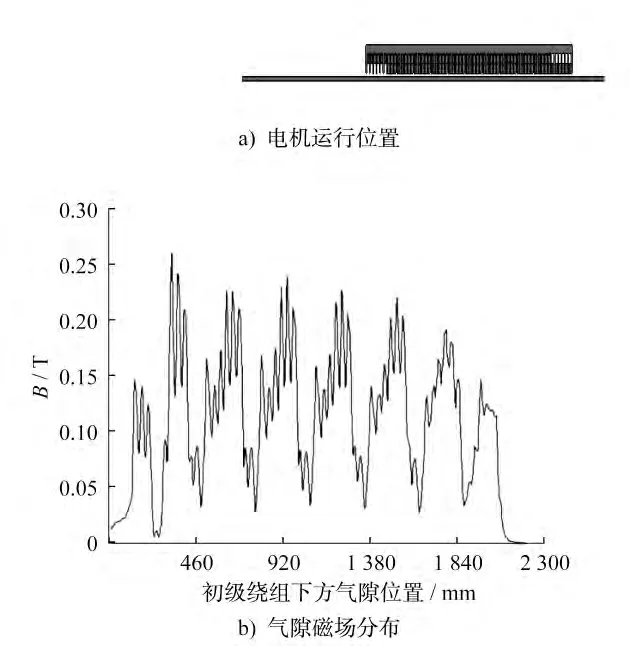
圖8 電機(jī)運(yùn)行位置與氣隙磁場(chǎng)分布圖（t＝2.3s）

4 結(jié)論

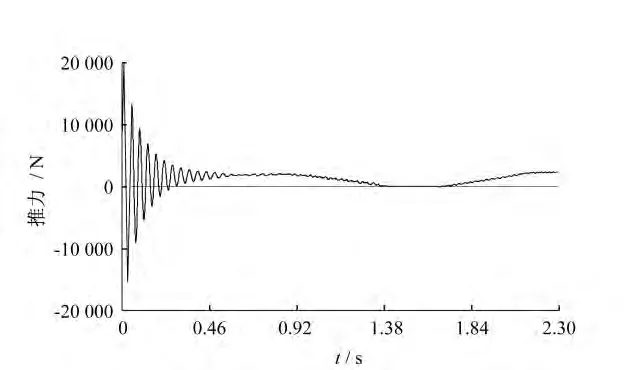
圖9 直線感應(yīng)電機(jī)的推力隨時(shí)間變化曲線

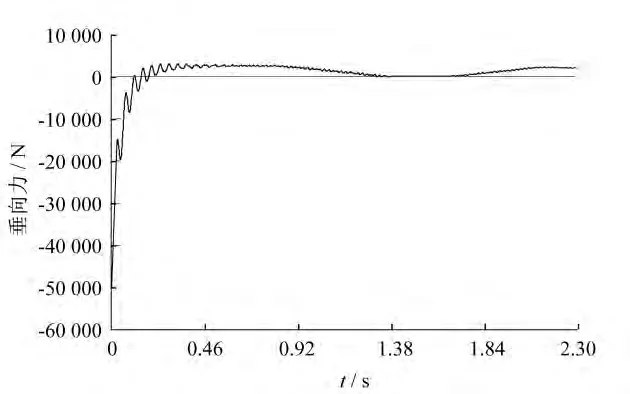
圖10 直線感應(yīng)電機(jī)的垂向力隨時(shí)間變化曲線

本文簡(jiǎn)析了直線感應(yīng)電機(jī)在軌道交通中的特性，運(yùn)用有限元方法，忽略橫向邊端效應(yīng)，并考慮道岔處感應(yīng)板不連續(xù)的情況，建立了牽引用直線感應(yīng)電機(jī)的二維瞬態(tài)電磁場(chǎng)模型；得到并分析了牽引用直線感應(yīng)電機(jī)的磁力線、推力、垂向力和氣隙磁場(chǎng)的特性曲線。仿真結(jié)果描述了直線感應(yīng)電機(jī)運(yùn)行至道岔區(qū)域時(shí)的變化規(guī)律，為牽引用直線感應(yīng)電機(jī)的電磁設(shè)計(jì)與控制方法的優(yōu)化提供了參考。

［1］鄭瓊林，趙佳，樊嘉峰.直線電機(jī)軌道交通牽引傳動(dòng)系統(tǒng)［M］.北京：中國(guó)科學(xué)技術(shù)出版社，2009：1.

［2］劉智成.直線電機(jī)運(yùn)載技術(shù)在廣州地鐵的應(yīng)用［J］.世界軌道交通，2005（3）：52.

［3］魏慶朝，蔡昌俊，龍?jiān)S友.直線電機(jī)軌道交通概論［M］.北京：中國(guó)科學(xué)技術(shù)出版社，2009：8.

［4］龍遐令.直線感應(yīng)電動(dòng)機(jī)的理論和電磁設(shè)計(jì)方法［M］.北京：科學(xué)出版社，2006：22.

［5］Im Dal－Ho，Kim Chang－Eob.Finite element force calculation of a linear induction motor taking account of the movement［J］.IEEE Transactions on Magnetics，1994，30（5）：3495.

［6］Nonaka S，Higuchi T.Design of single－sided linear induction motors for urban transit［J］.IEEE Transactions on Vehicular Technology，1988，37（3）：167.

［7］趙博，張洪亮.ansoft12在工程電磁場(chǎng)中的應(yīng)用［M］.北京：中國(guó)水利水電出版社.2010：130.

［8］郭明珠，方進(jìn)，李永亮，等.基于ANSYS的高溫超導(dǎo)直線感應(yīng)電機(jī)仿真分析［J］.超導(dǎo)技術(shù)，2008，36（3）：23.

［9］裘昌利，張紅梅，劉少克.基于Ansoft的直線感應(yīng)電機(jī)性能分析［J］.微特電機(jī)，2006（12）：22.