三維真比例導引彈道仿真分析

郝士林 嚴 超 雷 璐 畢 進

(西安電子工程研究所 西安 710100)

0 引言

比例導引法是在自尋的導彈上采用較多的一種導引規律，它是指導彈飛向目標的過程中，導彈速度方向的變化率與目標視線的成正比例。這種導引律有利于工程實現，同時選擇適合的導引比，就不會需要太大的法向過載，對不同機動特性的目標適應能力也較強［1］。而真比例導引律產生垂直于彈目視線的指令加速度，它與彈目視線距離變化率和彈目視線角速度變化率成正比，在命中點處的需用過載不僅與導彈速度無關，而且與導彈攻擊的方向也無關，相對于經典的比例導彈方法來說更具有優勢，有利于全向攻擊［2］。

1 三維真比例導引彈道仿真

1.1 彈目運動模型建立

在大地坐標系下分析攔截模型的運動參數，圖1表示某時刻彈目相對運動關系，T表示目標，M表示導彈，θt為目標速度傾角，θm為導彈彈道傾角，φt為目標速度偏角，φm為導彈彈道偏角。求解相關變量:

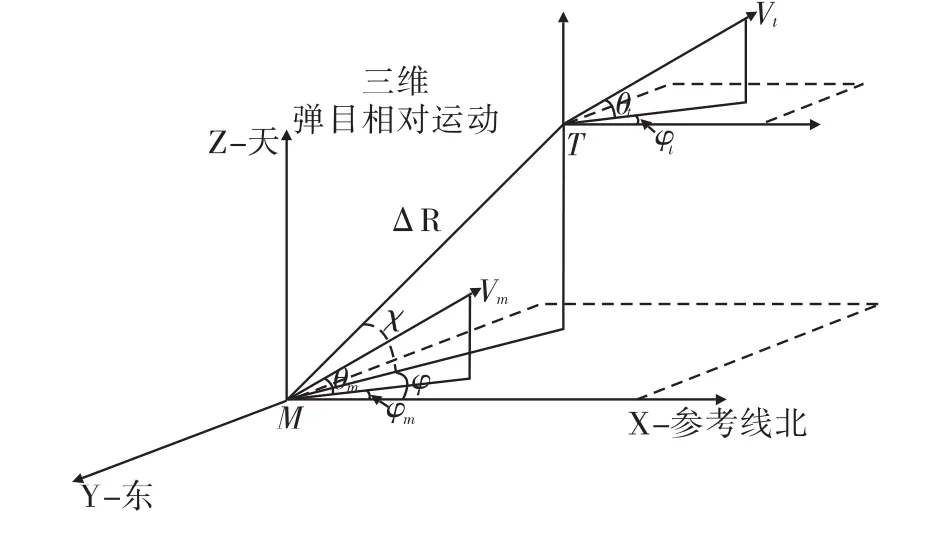
圖1 三維彈目相對運動示意圖

1.2 指令加速度方程

相關文獻［3-6］已經指出真比例導引律的指令加速度am施加于垂直于彈目視線的方向，其大小正比于彈目接近速度和視線角速率的乘積:

為了便于方程的計算，將導彈運動分解到垂直平面和水平面運動。即將產生的指令加速度分解為俯仰指令加速度和偏航指令加速度，其加速度方程:

1.3 仿真實現

A.仿真環境:vc++6.0，matlab 2010

B.仿真步長:10ms

C.目標運動參數:

目標初始為勻速直線運動，初始條件為a，當彈目距離為60km時，目標開始正弦機動機動條件滿足b，比例導引系數:k=3。

a.勻速情況

b.垂直平面正弦機動情況

T=20s，A=500m

D.

在VC下，通過4階龍格庫塔算法，對彈道方程求解后，存計算結果到本地文件。用matlab讀取仿真數據繪圖。仿真結果圖如下，圖2為彈目飛行曲線，OP和PM分別表示目標做勻速直線飛行和正弦機動飛行，與此對應的導引彈道為AB和BM。圖3、圖4、圖5為導彈的需用過載曲線，點B表示此時目標開始機動。

圖2 導引彈道圖

圖3 導彈x軸過載

圖4 導彈y軸過載

圖5 導彈z軸過載

1.4 仿真結果分析

圖1中，初始段OP目標勻速直線飛行，彈目相對距離較遠，彈目視線角速度變化均勻，致使需用指令加速度變化均勻，所以導引彈道AB段較平直。目標機動段PM，彈目視線角速度變化較大，所需加速度指令也發生較大變化，導引彈道BM相對彎曲;目標機動在彈目相對距離較遠時引起的視線角速度變化率比彈目距離較近時引起的視線角度變化率小，所以導引彈道BM段，前段比后段要緩一些。理論分析的指令加速度變化趨勢與實際仿真圖2、圖3和圖4是相符的。但在圖4中可以看出由于目標機動的原因，在末端導彈的需用過載很大，甚至很難實現，所以在對付大機動目標時制導精度較差。仿真結果與理論分析相符，驗證了將三維導引彈道分解計算的可行性。

2 結束語

本文基于飛行器真比例導引原理，建立彈目相對運動的導引方程，以龍格庫塔法為工具，以彈道投影分解計算為方法［7-9］，在VC環境下，對三維真比例導引彈道進行仿真。仿真結果與理論分析相符，表明了對三維導引彈道分解計算的可行性。友好的仿真環境以及通用的求解算法使程序具有較強的可移植性，而仿真中一些沒有考慮的諸因素，需要進一步分析研究。

［1］孫中南、童幼堂、張衛峰.比例導引法導引彈道仿真研究［J］.戰術導彈技術，2005，(2):56-59.

［2］錢杏芳、林瑞雄、趙亞男.導彈飛行力學［M］.北京:北京理工大學出版社，2011.

［3］衛星、王艷東.真比例導引律的解析解研究［J］.火力與指揮控制，2009，34(8):84-86.

［4］歐陽中輝、劉家祺、張龍杰、葉文.基于矢量運算的三維真比例導引彈道仿真［J］.彈箭與制導學報.2013，33(1):53-56.

［5］ 畢開波、王曉東、劉智平.飛行器制導與控制及其Matlab仿真技術［M］.北京:國防工業出版社，2009.

［6］ 李軍林、袁湛.三維修正比例導引彈道仿真研究［J］.機械管理開發，2009，(2):161-162.

［7］張建偉、黃樹彩、韓朝超.基于Matlab的比例導引彈道仿真分析［J］.戰術導彈技術，2009，(3):60-64.

［8］歐陽瑜、李剛、高忠長.基于Matlab的防空導彈三維彈道仿真［J］.火力與指揮控制，2010，35(2):166-168.

［9］趙蘊杰、曹迎春、張青斌.基于Matlab的三維動態彈道仿真研究［J］.計算機仿真，2007，24(6):57-61.