基于序列特征篩選與支持向量回歸預測蛋白質折疊速率

李 詠 周 瑋 代志軍 陳 淵 王志明 袁哲明

(湖南農業大學,湖南省作物種質創新與資源利用重點實驗室,長沙410128;湖南農業大學,湖南省植物病蟲害生物學及防控重點實驗室,長沙410128)

1 引言

多肽正確折疊成蛋白質才能發揮生物活性,錯誤的折疊不僅使蛋白質失活,且可導致瘋牛病、阿爾茨海默病等.1折疊速率預測對闡明蛋白質折疊機理意義重大,在酶工程、蛋白質工程等領域應用前景廣泛.質譜、核磁共振等傳統實驗測定折疊速率的方法耗時費力,2機器學習從已有數據出發,通過建立蛋白質折疊速率與諸因子之間的回歸模型,可實現折疊速率的快速預測并解析諸因子的影響大小,幫助認識折疊過程.

蛋白質按折疊類型分為二態、多態和混態三種,按結構類型分為全α、全β、混合型三種.目前已知折疊速率的蛋白質數量較少,按類型進一步細分后樣本容量偏小,建模時易出現過擬合、預測精度虛高;且待測蛋白質折疊類型或結構類型未知時,應用受限.故本文選擇統一建模,不按類細分樣本.

折疊速率預測的第一個關鍵是回歸模型選擇.由于蛋白質折疊是一個復雜的過程,且目前已知折疊速率的蛋白質數量較少,故本文選擇基于結構風險最小、非線性、適于小樣本的支持向量回歸(SVR)為基本建模工具.

折疊速率預測的第二個關鍵是蛋白質表征,包括三級結構、二級結構和一級結構表征描述符三類.三級結構表征的描述符如接觸序CO、總接觸序ACO和有效接觸序ECO等,3-8由于多數蛋白質三級結構尚未測定,應用受限.二級結構描述符如二級結構含量SSC、有效長度Leff等,9,10多從一級結構間接預測而得,描述符本身具有預測誤差,再次代入非線性SVR模型存在誤差放大風險,預測精度偏低.一級結構(氨基酸序列)描述符如CI、RSA、pse-ACC等,11-15多基于序列組分特征或以殘基某幾種物理化學性質直接算得,計算簡便,更具推廣應用價值;但存在組分特征未充分考慮序列的上下文關聯、殘基性質選擇多依賴經驗(與折疊速率相關的殘基性質不全、無關或冗余均會導致預測精度下降)、對不等長肽處理困難等弊端.

折疊速率預測的第三個關鍵是特征(描述符)篩選.特征篩選可去除無關與冗余描述符,但這種篩選過程同樣應該是非線性的.本實驗室16,17前期基于支持向量機(SVM)發展了高維特征選擇新方法二元矩陣重排過濾器(BMSF)與低維特征選擇新方法多輪末尾淘汰(WDEM).

綜上,本文僅基于氨基酸序列,提取多種組分特征與關聯特征,經改進BMSF與多輪末尾淘汰非線性篩選,建立了折疊速率與保留描述符的SVR回歸模型,進一步以SVR非線性解釋體系分析了各保留描述符對折疊速率的影響.

2 數據和方法

2.1 數據來源

115個蛋白質ID與對應的折疊速率值1,2,14,18見表1,氨基酸序列取自PDB數據庫(http://www.rcsb.org/pdb),折疊速率值以實驗值的自然對數lnkf表示,kf的單位為s-1.

2.2 序列表征

一條氨基酸序列可由其組分特征、上下文關聯特征與長度來特異性地表征.

2.2.1 天然氨基酸單殘基尺度組分特征

對長度為L的氨基酸序列,組分尺度為R,R個氨基酸殘基組成的串α1α2…αR可交疊出現頻次為f(α1α2…αR),其中αi,i=1,2,…R,代表20種天然氨基酸的一種,則α1α2…αR串在序列中出現概率為:

隨尺度變大,特征維數增加迅猛(如R=3,特征有8000維);而序列長度有限,特征矩陣將相當稀疏,對建模預測不利.故本文此處基于20種天然氨基酸僅提取單殘基尺度R=1的組分特征,其R=2時的二聯體組分特征將在下文k-space特征中k=0時涵蓋.每條序列可得20維特征.

2.2.2 重分類氨基酸多尺度組分特征

氨基酸重分類可降低特征維數,凸顯殘基某種性質的作用.20種天然氨基酸按支鏈官能團可分成8類(表2).取R=1-3,每條序列按式(1)可得8+64+512=584維多尺度組分特征.

2.2.3k-space特征

上述兩種組分特征僅考慮了3個以內殘基相鄰的情形,而蛋白質拓撲結構與穩定性和殘基的遠距離接觸有關,19且可由k-space一定程度表征.20種天然氨基酸相隔k個殘基的成對殘基在序列中出現概率(C)為:

表1 115個蛋白質樣品信息列表1,2,14,18Table 1 Information of 115 protein samples1,2,14,18

式中,k為space間隔,i和j為20種天然氨基酸中的一種,L為序列長度.n位置殘基為i,n+k位置殘基為j時Si,j(n,n+k)=1,否則為0.k-space既包含尺度為2的組分特征,又包含一定程度的上下文關聯特征.取k=0-10,每條序列可得400×11=4400維k-space特征.

表2 20種天然氨基酸分類Table 2 Classification of 20 natural amino acids

2.2.4 地統計學關聯(GSA)特征

k-space僅考慮了成對殘基間的上下文關聯.本文收集了20種天然氨基酸的544種物理化學性質(命名為PBF544),其中531種性質來自AAindex數據庫,2013種性質引自文獻.15,21,22因不同性質值差異較大,每種性質按20種氨基酸的最大最小值規格化到0-1之間.

地統計學基于區域化變量理論,引入半變異函數研究空間分布的結構性和隨機性,可用于表征蛋白質中全部殘基某種物理化學性質間的關聯且不受序列是否等長的限制.對長度為L的給定蛋白質序列,對應某一物理化學性質按PBF544可轉換為數值系列z(xi),i=1,2,…L,其半變異函數值r(h)為:

其中,h為間隔距離,N(h)為距離為h的數據對(xi,xi+h)的個數,z(xi)和z(xi+h)分別為點xi和點xi+h處殘基的物理化學性質值.

若數據集最短序列長度為Lmin,規定max(h)=INT(Lmin/2).本文數據集最短序列長度為16,h取1-8.則每條序列可得544×8=4352維地統計學關聯特征.

2.2.5 長度特征

前述組分特征等在計算概率時扣除了序列長度的影響,但多態折疊蛋白的折疊速率與序列長度負相關顯著,19故本文以lnL表征序列長度特征.

綜上,每條序列特征維數合計為20+584+4400+4352+1=9357.可以想象,其中必定存在大量與折疊速率無關或冗余的特征,需進行特征篩選.

2.3 特征篩選

2.3.1 高維特征粗篩

BMSF算法簡述如下:設單因變量原始訓練集形為(y,x),有n個樣本,m個特征.每個特征有1(選取)和0(不選取)兩種情形.產生一個元素為1或0的K×m隨機矩陣,限定每列1與0的個數相同,本文取K=500.從隨機矩陣的每行選取值為1的矩陣元素并找出原始訓練集中對應特征,以SVR經10折交叉測試獲得K個MSE值.K個MSE(因變量)與K×m隨機矩陣(自變量)組成新訓練集并訓練建模,隨機矩陣的某列元素0、1互換后(其它列不變)為測試集,預測得K個MSE0與K個MSE1,若則剔除相應特征;遍歷m次,得第一輪保留特征.重復上述過程,經多輪篩選至沒有特征可剔除為止.16,17

因BMSF中間矩陣是隨機生成的,不同次執行所得最優特征子集可能不同,本文對此進行改進:重復執行BMSF 50次,得到50套最優子集.合并出現頻次大于等于某個定值的特征產生頻次子集,根據10折交叉測試結果,得到更為可信的高頻特征子集.

2.3.2 多輪末尾淘汰精細篩選

WDEM算法簡述如下:對數據矩陣(yi,xij),i=1,2,…,n,j=1,2,…,m′,SVR交叉測試得初始MSE0,第一輪依次去除第j個特征,SVR交叉測試得到對應的MSEj,若min(MSEj)≤MSE0,則剔除相應特征并進入下一輪篩選,反之篩選結束.23,24

2.4 模型評估與解釋

基于保留描述符和全部樣本可構建SVR模型.模型評估常用交叉驗證、Jackknife檢驗或獨立測試.由于已知折疊速率的蛋白質樣本較少,同類研究常不劃分獨立測試集.為方便與文獻1,11-15進行比較,本文同樣采用Jackknife檢驗.評價指標為均方誤差(RMSE)和相關系數R,RMSE越小、R越大,回歸模型性能愈優:

式中,n為樣本數,yi和^i分別為第i個樣本的真值和預測值,為所有樣本真值的均值.

SVR缺乏一個顯性的表達式,可解釋性差.本室前期基于F測驗,對SVR建立了一套較完整的非線性解釋性體系,包括模型回歸顯著性測驗、單因子重要性顯著性測驗、單因子效應分析等,并驗證了其合理性與有效性.23,24F統計量由下式給出:

其中,U為回歸平方和:為剩余離差平方和:為保留特征數,F的自由度為表明在α水平上非線性回歸顯著.

本文BMSF高維特征粗篩、多輪末尾淘汰精篩、SVR建模和非線性解釋體系等采用自編MATLAB程序通過調用LIBSVM3.1軟件包25實現.多數情況下徑向基核較其它核函數有更優的泛化推廣能力,26本文試算后核函數選用徑向基核.核函數參數采用Python默認范圍、步長經格點搜索自動獲取.

2.5 參比模型

文獻參比模型包括多元線性回歸(MLR)、基于SVR的前向-序貫后向特征選擇方法(FFS-SBSSVR);基于本文描述符的參比模型包括SVR、遺傳算法-偏最小二乘(GA-PLS)、27嶺回歸與SVR(RRSVR).28

3 結果與分析

基于115個樣本和9357個初始特征,數據集10折交叉測試的RMSE=3.94,R=0.30.50次BMSF高維特征初篩后,得到50套子集,分別進行多輪末尾淘汰,平均保留特征個數、RMSE、R分別為31、1.59、0.91,可見特征篩選效果明顯.合并出現頻次大于等于某個定值的特征產生頻次特征子集,頻次子集進行10折交叉測試,結果見圖1,可見出現7次及以上的特征10折交叉測試RMSE最小、R最大.故合并出現頻次大于等于7次的特征得到高頻最優特征子集.對高頻最優特征子集進一步實施多輪末尾淘汰精篩,最終得到23個保留描述符.

基于23個保留描述符建立SVR23模型,其F=63.42>F0.01/23(23,91)=2.70,表明模型非線性回歸極顯著.SVR23模型Jackknife檢驗的實驗值與預測值見表1和圖2,其R=0.95,RMSE=1.34.可見,改進BMSF進一步提高了模型精度、減少了保留描述符個數.

圖1 不同頻次子集10折交叉測試的RMSE和RFig.1 RMSE and R values of 10-fold cross-validation of different frequency subsets

圖2 Jackknife交叉檢驗的蛋白質折疊速率實驗值與預測值Fig.2 Relationship between the experimental and predicted protein folding rates with Jackknife cross-validation

參比模型中,GA-PLS選取3個潛變量;RRSVR先經嶺回歸篩選得121個描述符,再經多輪末尾淘汰得到23個保留描述符.各模型Jackknife檢驗結果列于表3.可見,SVR23在所有參比模型中表現最優.

23個保留描述符包括1個長度特征、12個kspace特征、8個地統計學關聯特征和2個氨基酸分八類時的三聯體特征(表4),可見:(1)序列長度是影響蛋白質折疊速率的最重要因素.早期研究認為二態折疊蛋白折疊速率與序列長度的相關性較低,3但隨后發現多態折疊蛋白折疊速率與序列長度顯著負相關,19且序列長度的自然對數lnL優于其它形式(L,L1/2,L2/3).29(2)單個氨基酸組成(無論是分20類還是分8類)對折疊速率影響不大.(3)地統計學關聯特征多涉及殘基形成α-helix、β-turn等二級結構性質,且以中短程關聯為主(h=1-6).(4)k-space反映的是成對殘基間的關聯,保留描述符中成對殘基較為分散,以脂肪族氨基酸殘基為主,且T、P、W、C殘基參與的成對殘基無一入選,關聯距離k=1-10,k=0反映的相鄰殘基對(二聯體)無一入選.脂肪族氨基酸含有疏水側鏈,在蛋白質折疊過程中有序聚集,形成疏水內部結構,影響蛋白質折疊速率.1(5)氨基酸分八類時,疏水脂肪氨基酸+酰胺+疏水脂肪氨基酸、酸性氨基酸+酸性氨基酸+羥基氨基酸的兩種三聯體對折疊速率有重要影響.綜上,蛋白質折疊速率與序列長度、三聯體殘基組分特征、中短程關聯特征等相關密切.

保留描述符的單因子重要性、顯著性測驗結果表明,其F值均大于臨界值F0.01/23(1,91)(13.33),保留描述符對蛋白質折疊速率的影響極顯著(表4).其單因子效應分析結果見圖3,可見23個保留描述符可明顯分為三類:第一類為序列長度(No.1)和地統計學關聯特征(No.2、No.4、No.5、No.7、No.13),其排序整體較為靠前,與折疊速率負相關;第二類是8個kspace 特 征 (No.3、No.12、No.15、No.16、No.18、No.20、No.22、No.23)和1個氨基酸分八類時的三聯體特征(No.10),與折疊速率同樣均為負相關;第三類特征與折疊速率正相關,包括1個氨基酸分八類時的三聯體特征(No.6)、4個k-space特征(No.8、No.9、No.11、No.21)和 3 個地統計學關聯特征(No.14、No.17、No.19).

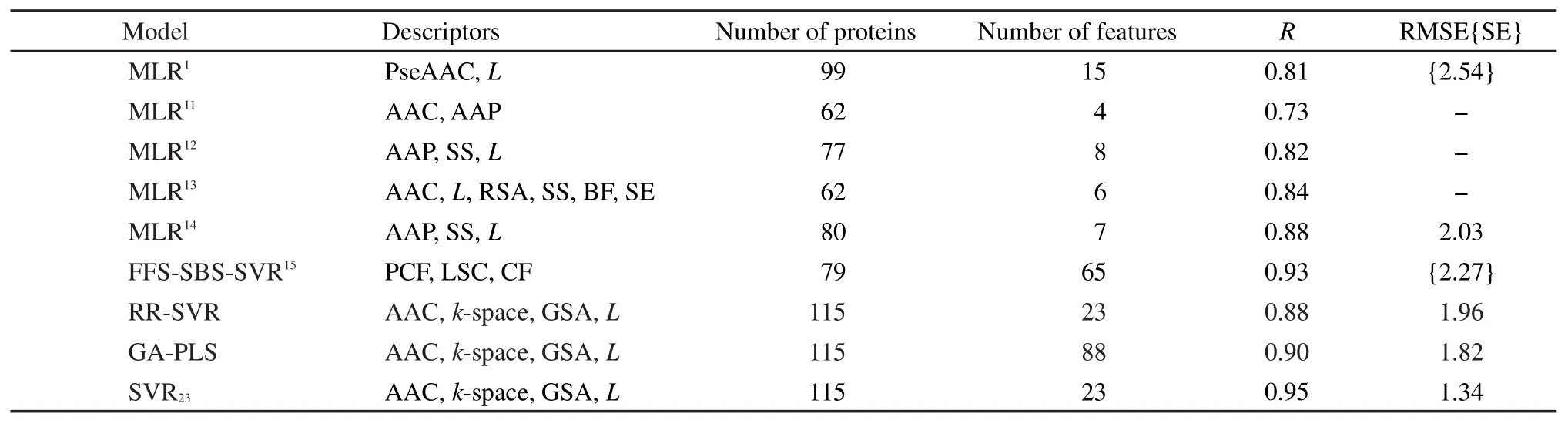
表3 Jackknife交叉驗證結果比較Table 3 Comparison of Jackknife cross-validation results

表4 篩選后保留的23個特征Table 4 23 retained features after feature screening

圖3 折疊速率相關的23個保留描述符的單因子效應Fig.3 Single-factor effects of 23 retained descriptors on protein folding rate

4 小結與討論

包括多種組分、上下文關聯與長度在內的9357個描述符較完整地表征了一條蛋白質序列,但其中存在大量與折疊速率無關或冗余的特征,經改進的BMSF非線性粗篩和多輪末尾淘汰精細篩選,保留了23個物化意義明確的特征,建立的SVR模型非線性回歸極顯著,獲得了優于文獻報道的留一法預測精度.單因子效應分析顯示,23個保留描述符可明顯分為三類:第一類與折疊速率負相關,包括序列長度和5個地統計學關聯特征;第二類與折疊速率同樣負相關,包括8個k-space特征和1個氨基酸分八類時的三聯體特征;第三類與折疊速率正相關,包括1個氨基酸分八類時的三聯體特征、4個kspace特征和3個地統計學關聯特征.蛋白質折疊速率主要受序列長度、中短程關聯特征、三聯體殘基組份特征等影響.

蛋白質折疊是一個非常復雜的過程,本文僅基于一級序列,未涉及蛋白質高級結構特征;折疊速率實驗值取自不同文獻,實驗環境的差異如溫度也未能考慮.本文結果存在進一步改進空間,同時需更多樣本驗證支持.

(1) Guo,J.X.;Rao,N.N.;Liu,G.X.;Li,J.;Wang,Y.H.Prog.Biochem.Biophys.2010,37(12),1331.[郭建秀,饒妮妮,劉廣雄,李 杰,王云鶴.生物化學與生物物理進展,2010,37(12),1331.]

(2) Xi,L.L.;Li,S.Y.;Liu,H.X.;Li,J.Z.;Lei,B.L.;Yao,X.J.J.Theor.Biol.2010,264(4),1159.doi:10.1016/j.jtbi.2010.03.042

(3) Plaxco,K.W.;Simons,K.T.;Baker,D.J.Mol.Biol.1998,277(4),985.doi:10.1006/jmbi.1998.1645

(4) Ivankov,D.N.;Garbuzynskiy,S.O.;Alm,E.;Plaxco,K.W.;Baker,D.;Finkelstein,A.V.Protein Sci.2003,12(9),2057.doi:10.1110/ps.0302503

(5) Weikl,T.R.;Dill,K.A.J.Mol.Biol.2003,332(4),953.doi:10.1016/S0022-2836(03)00884-2

(6) Zhang,L.X.;Li,J.;Jiang,Z.T.;Xia,A.G.Polymer2003,44(5),1751.doi:10.1016/S0032-3861(03)00021-1

(7) Capriotti,E.;Casadio,R.Bioinformatics2007,23(3),385.doi:10.1093/bioinformatics/btl610

(8) Ivankov,D.N.;Bogatyreva,N.S.;Lobanov,M.Y.;Galzitskaya,O.V.PLoS One2009,4(8),e6476.

(9) Gong,H.P.;Isom,D.G.;Srinivasan,R.;Rose,G.D.J.Mol.Biol.2003,327(5),1149.doi:10.1016/S0022-2836(03)00211-0

(10) Ivankov,D.N.;Finkelstein,A.V.Proc.Natl.Acad.Sci.U.S.A.2004,101(24),8942.doi:10.1073/pnas.0402659101

(11) Ma,B.G.;Guo,J.X.;Zhang,H.Y.Proteins:Struct.,Funct.,Bioinf.2006,65(2),362.doi:10.1002/prot.21140

(12) Jiang,Y.F.;Iglinski,P.;Kurgan,L.J.Comput.Chem.2009,30(5),772.doi:10.1002/jcc.21096

(13) Gao,J.Z.;Zhang,T.;Zhang,H.;Shen,S.Y.;Ruan,J.S.;Kurgan,L.Proteins:Struct.,Funct.,Bioinf.2010,78(9),2114.

(14) Shen,H.B.;Song,J.N.;Chou,K.C.J.Biomed.Sci.Eng.2009,2(3),136.doi:10.4236/jbise.2009.23024

(15)Cheng,X.;Xiao,X.;Wu,Z.C.;Wang,P.;Lin,W.Z.Proteins:Struct.,Funct.,Bioinf.2013,81(1),140.doi:10.1002/prot.24171

(16)Zhang,H.Y.;Wang,H.Y.;Dai,Z.J.;Chen,M.S.;Yuan,Z.M.BMC Bioinformatics2012,13(1),298.doi:10.1186/1471-2105-13-298

(17)Han,N.;Yuan,Z.M.;Chen,Y.;Dai,Z.J.;Wang,Z.M.Acta Phys.-Chim.Sin.2013,29(9),1945.[韓 娜,袁哲明,陳 淵,代志軍,王志明.物理化學學報,2013,29(9),1945.]doi:10.3866/PKU.WHXB201306182

(18)Guo,J.X.;Rao,N.N.;Liu,G.X.;Yang,Y.;Wang,G.J.Comput.Chem.2011,32(8),1612.doi:10.1002/jcc.21740

(19) Galzitskaya,O.V.;Garbuzynskiy,S.O.;Ivankov,D.N.;Finkelstein,A.V.Proteins:Struct.,Funct.,Genet.2003,51(2),162.doi:10.1002/prot.10343

(20) Kawashima,S.;Pokarowski,P.;Pokarowska,M.;Kolinski,A.;Katayama,T.;Kanehisa,M.Nucl.Acids Res.2008,36(suppl.1),D202.

(21) Gromiha,M,M.;Selvaraj,S.Prep.Biochem.Biotechnol.1999,29(4),339.doi:10.1080/10826069908544933

(22) Zhou,P.;Tian,F.F.;Li,B.;Wu,S.R.;Li,Z.L.Acta Chim.Sin.2006,64(7),691.[周 鵬,田菲菲,李 波,吳世容,李志良.化學學報,2006,64(7),691.]

(23)Tan,X.S.;Wang,Z.M.;Tan,S.Q.;Yuan,Z.M.;Xiong,X.Y.J.Syst.Simul.2009,21(24),7795.[譚顯勝,王志明,譚泗橋,袁哲明,熊興耀.系統仿真學報,2009,21(24),7795.]

(24) Dai,Z.J.;Zhou,W.;Yuan,Z.M.Acta Phys.-Chim.Sin.2011,27(7),1654.[代志軍,周 瑋,袁哲明.物理化學學報,2011,27(7),1654.]doi:10.3866/PKU.WHXB20110735

(25) Chang,C.C.;Lin,C.J.ACM TIST.2011,2(3),27.

(26)Chen,Y.;Yuan,Z.M.;Zhou,W.;Xiong,X.Y.Acta Phys.-Chim.Sin.2009,25(8),1587.[陳 淵,袁哲明,周 瑋,熊興耀.物理化學學報,2009,25(8),1587.]doi:10.3866/PKU.WHXB20090752

(27) Leardi,R.J.Chemometr.2000,14(5-6),643.doi:10.1002/1099-128X(200009/12)14:5/6<643::AID-CEM621>3.0.CO;2-E

(28)Wang,Z.M.;Han,N.;Yuan,Z.M.;Wu,Z.H.Acta Phys.-Chim.Sin.2013,29(3),498.[王志明,韓 娜,袁哲明,伍朝華.物理化學學報,2013,29(3),498.]doi:10.3866/PKU.WHXB201301042

(29) Ouyang,Z.;Liang,J.Protein Sci.2008,17(7),1256.doi:10.1110/ps.034660.108