一種RVM的INS參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償方法

黨宏濤，伊國興，于湘濤，杜祖良，，王常虹

（1.哈爾濱工業(yè)大學(xué)空間控制與慣性技術(shù)研究中心，150001哈爾濱；

2.北京自動化控制設(shè)備研究所，100074北京；3.解放軍96117部隊，271100山東萊蕪）

一種RVM的INS參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償方法

黨宏濤1，3，伊國興1，于湘濤2，杜祖良1，2，王常虹1

（1.哈爾濱工業(yè)大學(xué)空間控制與慣性技術(shù)研究中心，150001哈爾濱；

2.北京自動化控制設(shè)備研究所，100074北京；3.解放軍96117部隊，271100山東萊蕪）

為提高慣導(dǎo)系統(tǒng)參數(shù)長期穩(wěn)定性，降低人工標(biāo)定成本，增強(qiáng)慣導(dǎo)系統(tǒng)使用效能，提出一種基于相關(guān)向量機(jī)的慣導(dǎo)系統(tǒng)參數(shù)長期穩(wěn)定性預(yù)測和補(bǔ)償方法，選擇均值和標(biāo)準(zhǔn)差作為參數(shù)穩(wěn)定性的性能指標(biāo).而對于均值隨時間變化具有明顯規(guī)律的參數(shù)，采用RVM方法對存貯時間較長的參數(shù)穩(wěn)定性均值進(jìn)行回歸建模，根據(jù)模型對存貯時間較短的參數(shù)穩(wěn)定性進(jìn)行性能預(yù)測和標(biāo)定參數(shù)補(bǔ)償.最后對慣導(dǎo)系統(tǒng)中重要參數(shù)加速度計標(biāo)度因數(shù)長期穩(wěn)定性進(jìn)行建模預(yù)測和參數(shù)補(bǔ)償，補(bǔ)償后結(jié)果顯示，間隔時間約6個月的參數(shù)穩(wěn)定性均值性能提高了50.90%，驗證了所提方法具有很好的實際應(yīng)用價值，且表明使用該方法能夠代替人工標(biāo)定，以增強(qiáng)慣導(dǎo)系統(tǒng)使用效能.

相關(guān)向量機(jī)；慣導(dǎo)系統(tǒng)；標(biāo)定周期；長期穩(wěn)定性；預(yù)測補(bǔ)償

慣性導(dǎo)航系統(tǒng)（inertial navigation system，INS）標(biāo)定參數(shù)長期穩(wěn)定性是衡量產(chǎn)品綜合性能的重要指標(biāo).為了保證INS綜合性能滿足要求，需要間隔一定時間對影響INS綜合性能的各項參數(shù)進(jìn)行穩(wěn)定性標(biāo)定.對于軍方用戶來說，提高參數(shù)長期穩(wěn)定性性能意味著戰(zhàn)時具有更大主動性和生存能力［1］.

通過對慣導(dǎo)系統(tǒng)產(chǎn)品機(jī)理［2-3］和標(biāo)定方法［4］的研究都能夠有效提高參數(shù)穩(wěn)定性性能，但通過對批量歷次標(biāo)定參數(shù)長期穩(wěn)定性預(yù)測和補(bǔ)償方法研究來提高INS參數(shù)穩(wěn)定性性能，在國內(nèi)尚無研究.近年來，基于支持向量機(jī)（SVM）［5］的統(tǒng)計分析方法和基于稀疏貝葉斯［6］的統(tǒng)計分析方法成為機(jī)器學(xué)習(xí)領(lǐng)域的研究熱點［7-8］.支持向量機(jī)采用VC維理論和結(jié)構(gòu)風(fēng)險最小化原則，對于小樣本情況下的模型具有很好的泛化能力，但由于SVM所需核函數(shù)的數(shù)量會隨著訓(xùn)練集增大而顯著增加，同時預(yù)測也缺乏必要的概率信息［9］；基于稀疏貝葉斯的相關(guān)向量機(jī)（RVM）是一種與SVM函數(shù)形式相同的稀疏概率模型，與SVM相比它不存在以上缺點，在實際預(yù)測性能相當(dāng)?shù)那闆r下，解的稀疏性明顯高于SVM［10］.

由于INS歷次標(biāo)定參數(shù)隨時間變化所積累數(shù)據(jù)較少，對穩(wěn)定性進(jìn)行估計得到均值性能具有一定的不確定性，因此本文嘗試著用先進(jìn)智能算法解決INS參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償遇到的實際工程問題.

1 RVM建模方法

RVM比較適用于函數(shù)回歸和分類，它把基于高斯過程的貝葉斯推理方法應(yīng)用到支持向量機(jī)中.

1.1 RVM基本理論

給定輸入向量x=｛xn｜n=1，2，…，N｝和相應(yīng)的輸出向量t=｛tn｜n=1，2，…，N｝，通過應(yīng)用訓(xùn)練數(shù)據(jù)和先驗知識設(shè)計RVM回歸模型，令

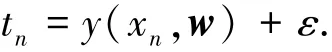
式中:tn是目標(biāo)值；w=（w0，w1，…，wN）是可調(diào)參數(shù)權(quán)值；ε=｛εn｜n=1，2，…，N｝是獨立分布的零均值高斯噪聲，其方差為σ2；未知函數(shù)y可以表示為

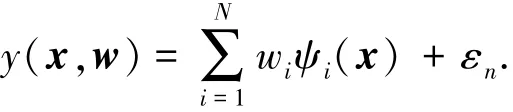
式中ψi（x）=K（x，xi）為核函數(shù)．

假定tn相互獨立，則已知訓(xùn)練集的似然估計可寫為

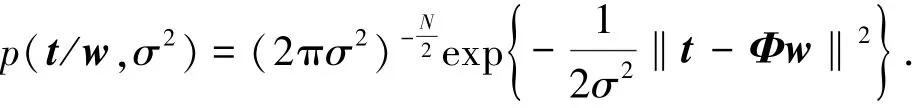
采用稀疏貝葉斯原理對w進(jìn)行零均值高斯先驗分布:

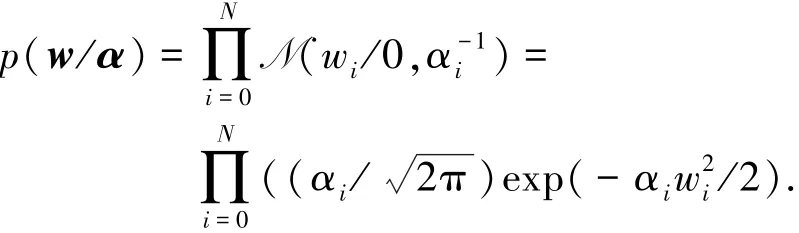
式中:α為N+1維超參數(shù)向量，每1個權(quán)重wi對應(yīng)1個超參數(shù)αi，從而控制先驗分布對各參數(shù)的影響，以確保相關(guān)向量模型的稀疏性．

根據(jù)貝葉斯原理，對所有未知參數(shù)有如下后驗公式:

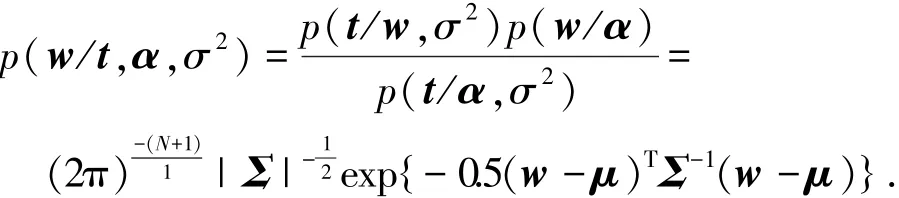
式中:Σ為后驗協(xié)方差矩陣，Σ=（σ-2ΦTΦ+ A）-1；A為對稱矩陣，A=diag（α0，α1，…，αN）；μ為均值向量，μ=σ-2∑ΦTt；Φ為N×（N+1）維矩陣，

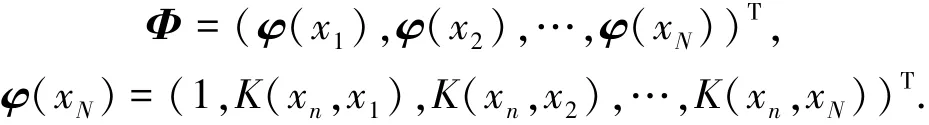
對于α和σ2，使用迭代公式進(jìn)行估計:

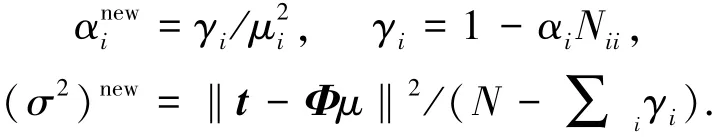
式中:γi為衡量α的中間變量；μi為第i個后驗平均權(quán)；Nii為后驗權(quán)協(xié)方差矩陣的第i個對角元素；N為樣本數(shù)據(jù)個數(shù)．

若給定一個輸入值x?，則相應(yīng)的輸出值概率分布為

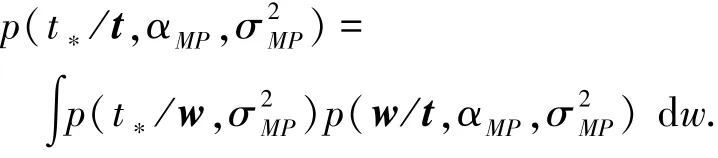
上式服從高斯分布，且

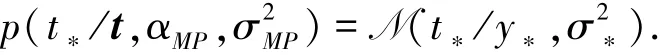
式中αMP、σ為經(jīng)過迭代用于預(yù)測的最優(yōu)值．預(yù)測方差預(yù)測均值y?=μTφ（x?），y?為t?的預(yù)測值．

1.2 RVM核函數(shù)的確定

RVM常用的幾種核函數(shù)有RBF核函數(shù)、線性核函數(shù)、多項式核函數(shù)等.其中，RBF核函數(shù)具有較好的學(xué)習(xí)能力，適用于高維、低維、小樣本、大樣本等多種情況［11］.因此，本文選用RBF函數(shù)作為RVM的核函數(shù)，其數(shù)學(xué)表達(dá)式為

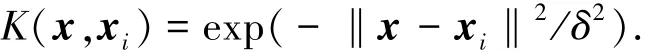
式中:x為目標(biāo)輸入向量；xi為訓(xùn)練樣本中第i維輸入向量；δ2為核函數(shù)的寬度．

1.3 蟻群優(yōu)化算法

蟻群優(yōu)化算法（ant colony optimization，ACO）是20世紀(jì)90年代提出的一種新型模擬自然界生物系統(tǒng)的智能算法，具有良好的并行分布性、自組織性、正反饋特性，從理論上保證了算法能夠在較短的時間里找到全局最優(yōu)解.在采用徑向基函數(shù)作為RVM核函數(shù)時需要對參數(shù)δ2進(jìn)行優(yōu)化，以保證RVM模型具有較高的擬合度，用蟻群優(yōu)化算法的RVM計算步驟如下:

1）參數(shù)初始化.設(shè)有m個螞蟻，第i個螞蟻的初始位置Si=δi，i=1，2，…，m．

2）信息素初始化．對m個螞蟻所在位置的目標(biāo)值進(jìn)行計算，根據(jù)目標(biāo)值的滿意程度來確定其所在位置信息素的大小:Δt（i）=αE（i），初始信息素定為T0（1）=Δt（1），E（i）為第i個螞蟻所在位置對目標(biāo)值的滿意度，α為已設(shè)定的值，一般取α=3．

3）信息素的揮發(fā)和更新.

建立揮發(fā)因子:ρ=ln（（K-i）／K），i=1，2，…，K-1，K為蟻群總的迭代次數(shù)；

更新信息素:T（i）=（1-ρ）T（i-1）+Δt（i）．

4）通過信息素的大小，確定螞蟻下一步轉(zhuǎn)移的概率:p（i）=eT0（best）-T0（i）／eT0（best），其中T0（best）是信息素最大的螞蟻．

5）螞蟻位置的更新:

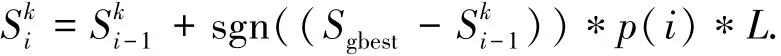
6）根據(jù)尋找到的最優(yōu)解Sgbest=δ?，進(jìn)行RVM預(yù)測建模．

2 INS參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償

INS標(biāo)定參數(shù)長期穩(wěn)定性包括陀螺常值漂移、陀螺力矩器系數(shù)、陀螺與G有關(guān)項、航向效應(yīng)、加速度計零偏、加速度計標(biāo)度因數(shù)等多項參數(shù)，通過對歷次標(biāo)定數(shù)據(jù)進(jìn)行整理，發(fā)現(xiàn)加速度計標(biāo)度因數(shù)變化趨勢最為明顯，因此本文選擇加速度計標(biāo)度因數(shù)進(jìn)行參數(shù)長期穩(wěn)定性預(yù)測和補(bǔ)償.

2.1 參數(shù)長期穩(wěn)定性數(shù)據(jù)整理

標(biāo)定參數(shù)穩(wěn)定性是指以第一次標(biāo)定數(shù)據(jù)為基準(zhǔn)，后續(xù)標(biāo)定的數(shù)據(jù)減去第一次標(biāo)定數(shù)據(jù)，其時間間隔為兩次標(biāo)定的時間差，INS穩(wěn)定性包含產(chǎn)品編號、穩(wěn)定性數(shù)據(jù)、穩(wěn)定性時間間隔，經(jīng)過對批次產(chǎn)品標(biāo)定參數(shù)進(jìn)行異常數(shù)據(jù)的剔除和修訂，得到穩(wěn)定性樣本為S｛（xp，tp）｜p=1，2，…，K｝，=f（）表示第p個產(chǎn)品某項參數(shù)長期穩(wěn)定性在時間間隔x時所對應(yīng)的數(shù)值．

2.2 參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償流程

不同批次的INS產(chǎn)品，當(dāng)系統(tǒng)結(jié)構(gòu)、生產(chǎn)工藝、標(biāo)定設(shè)備、標(biāo)定方法，貯存環(huán)境等因素相同時，INS參數(shù)隨時間變化的具有類似的趨勢.在實際應(yīng)用中，首先需要對存貯時間長和標(biāo)定次數(shù)多的參數(shù)穩(wěn)定性進(jìn)行趨勢性判斷，對于穩(wěn)定性均值性能趨勢變化明顯的參數(shù)，進(jìn)行RVM預(yù)測，根據(jù)預(yù)測模型，對存貯時間短的參數(shù)進(jìn)行當(dāng)前時間的穩(wěn)定性預(yù)測，并對預(yù)測值進(jìn)行補(bǔ)償，將補(bǔ)償后的INS快速裝配到武器系統(tǒng)，避免了對INS進(jìn)行耗時耗力的人工標(biāo)定.基于RVM的INS參數(shù)穩(wěn)定性預(yù)測與補(bǔ)償流程圖如圖1所示.

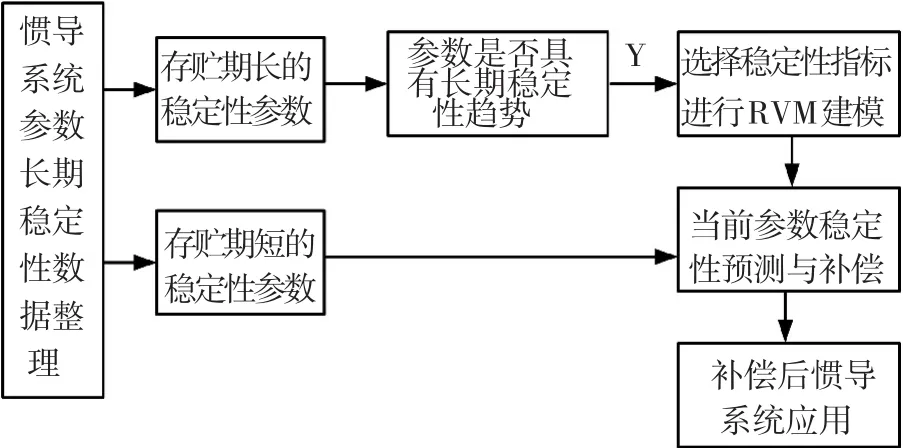
圖1 參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償流程

3 方法驗證

加速度計是INS的重要部件，其標(biāo)度因數(shù)長期穩(wěn)定性對INS綜合性能有重要影響，采用基于RVM的方法對其參數(shù)長期穩(wěn)定性進(jìn)行建模、預(yù)測和補(bǔ)償.

3.1 標(biāo)度因數(shù)長期穩(wěn)定性預(yù)測模型

選擇兩個批次的INS加速度標(biāo)度因數(shù)長期穩(wěn)定性進(jìn)行整理，第X9批次為24臺INS，共計72組加速度計標(biāo)度因數(shù)，第X3批次為39臺INS，共計117組加速度計標(biāo)度因數(shù)，如圖2所示.

圖2 兩個批次產(chǎn)品標(biāo)度因數(shù)長期穩(wěn)定性

圖2 每條曲線表示每塊加速度計標(biāo)度因數(shù)，星點表示穩(wěn)定性隨時間間隔的變化數(shù)據(jù).對每個時間段上的標(biāo)度因數(shù)穩(wěn)定性，采用平均值和標(biāo)準(zhǔn)差對總體性能進(jìn)行評價，均值隨時間變化表示了參數(shù)系統(tǒng)誤差隨時間的變化趨勢，具有可補(bǔ)償性，標(biāo)準(zhǔn)差隨時間變化表示了參數(shù)隨機(jī)誤差隨時間的變化趨勢，具有不可補(bǔ)償性.選擇圖2（a），對參數(shù)穩(wěn)定性隨時間變化進(jìn)行RVM預(yù)測建模，為了便于計算，將圖2（a）按照9個時間間隔點整理，得到的RVM預(yù)測模型如圖3所示.

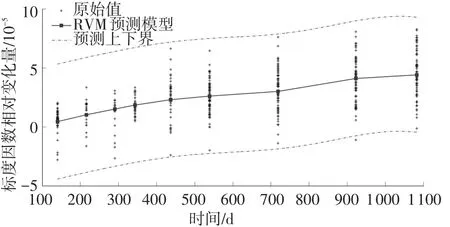
圖3 第X9批次標(biāo)度因數(shù)穩(wěn)定性RVM預(yù)測模型

從圖3可以看出，標(biāo)度因數(shù)長期穩(wěn)定性具有時間明顯變化的趨勢，在采用蟻群優(yōu)化算法對參數(shù)δ進(jìn)行優(yōu)化的情況下，當(dāng)δ=0.353 7時，得到RVM預(yù)測模型均方誤差為0.026 2，模型標(biāo)準(zhǔn)差為0.162 1.

3.2 標(biāo)度因數(shù)長期穩(wěn)定性預(yù)測補(bǔ)償模型及驗證

選擇存貯時間較短的圖2（b）第X3批次標(biāo)度因數(shù)進(jìn)行RVM預(yù)測和補(bǔ)償驗證.

根據(jù)RVM模型，建立參數(shù)長期穩(wěn)定性RVM預(yù)測補(bǔ)償模型，設(shè)定最后兩次標(biāo)定時間間隔Δx= xn-xn-1的穩(wěn)定性變化量Δt?:

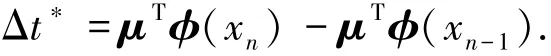
令

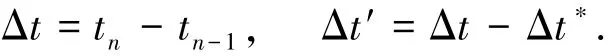
式中:Δt?為預(yù)測補(bǔ)償值；Δt為實際參數(shù)長期穩(wěn)定性；Δt′為RVM預(yù)測補(bǔ)償后的參數(shù)長期穩(wěn)定性．

對Δt和Δt′進(jìn)行驗證對比，結(jié)果如圖4所示．

從圖4可知，117組加速度計標(biāo)度因數(shù)兩次標(biāo)定時間間隔約為6個月（180 d），未補(bǔ)償時，標(biāo)度因數(shù)參數(shù)穩(wěn)定性平均值為1.918×10-5，經(jīng)過預(yù)測補(bǔ)償后，其參數(shù)穩(wěn)定性平均值為9.419 2×10-6.

4 結(jié) 語

為了提高INS參數(shù)長期穩(wěn)定性性能，增強(qiáng)INS使用效能，針對INS中部分參數(shù)長期穩(wěn)定性具有明顯變化的趨勢，提出了基于RVM的參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償方法.通過對某型INS加速度計標(biāo)度因數(shù)長期穩(wěn)定性進(jìn)行預(yù)測和補(bǔ)償，結(jié)果表明經(jīng)過補(bǔ)償后參數(shù)長期穩(wěn)定性均值性能提高了50.90%.表明基于RVM的參數(shù)長期穩(wěn)定性預(yù)測與補(bǔ)償方法具有一定的工程價值，結(jié)合實際開展進(jìn)一步的應(yīng)用研究對提高INS系統(tǒng)的精度、延長標(biāo)定周期具有重要意義.

［1］張洪立，許奔.SiC／Al技術(shù)延長慣性平臺標(biāo)定周期的理論研究［J］.中國慣性技術(shù)學(xué)報，2003，11（5）: 16-18.

［2］SHIZhen，YANG Jie，YUEPeng，etal.A new calibration and compensation method for installation errors of accelerometers in Gyroscope Free Strap-down Inertial Navigation System［C］／／2010 IEEE International Conference on Information and Automation（ICIA）. Piscataway:IEEE，2010:924-929.

［3］林玉榮，鄧正隆.激光陀螺捷聯(lián)慣導(dǎo)系統(tǒng)中慣性器件誤差的系統(tǒng)級標(biāo)定［J］.哈爾濱工業(yè)大學(xué)學(xué)報，2001，33（1）:112-115.

［4］曹淵，張士峰，楊華波，等.慣導(dǎo)平臺誤差快速自標(biāo)定方法研究［J］.宇航學(xué)報，2011，32（6）: 1281-1287.

［5］VAPNIK V.N.Statistical learning theory［M］.New York:John Wiley，1998:17-25.

［6］YUAN Jin，BO Liefeng，WANG Kesheng，et al. Adaptive spherical Gaussian kernel in sparse Bayesian learning framework for nonlinear regression［J］.Expert Systemswith Applications.2009，36（2）:3982-3989.

［7］張宇航，張曄.SVM和RVM對高光譜圖像分類的應(yīng)用潛能分析［J］.哈爾濱工業(yè)大學(xué)學(xué)報，2012，44（3）:34-39.

［8］申爭光，朱鳳宇，王祁.基于PFP-WRVM的多功能傳感器狀態(tài)自確認(rèn)研究［J］.儀器儀表學(xué)報，2012，33（9）:1986-1994.

［9］SILVA C，RIBEIRO B.Two-level hierarchical hybrid SVM-RVM classification model［C］／／5th International Conference on Machine Learning and Applications. Orlando，F(xiàn)L:ICMLA，2006:89-94.

［10］WANG Haiying，ZHENG Huiru.A bayesian approach to improving decision making in support vector machine and its application in bioinformatics［C］／／Fifth International Conference on Natural Computation. Tianjin:ICNC，2009（2），89-93.

［11］DI You，HAMSICI O C，MARTINEZ A M.Kernel optimization in discriminant analysis［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（3）:631-638.

（編輯張 宏）

RVM-based prediction and com pensation method for the long-term stability of INS system parameters

DANG Hongtao1，3，YIGuoxing1，YU Xiangtao2，DU Zuliang1，2，WANG Changhong1

（1.Space Control and Inertial Technology Research Center，Harbin Institute of Technology，150001 Harbin，China；2.Beijing Institute of Automatic Control Equipment，100074 Beijing，China；3.96117 Troops，271100 Shandong Laiwu，China）

To improve the long-term stability performance，reduce the manual calibration costs and enhance the use efficiency of inertial navigation systems，we propose a prediction and compensation method for the long-term stability of inertial navigation system parameter based on correlation vector machine，in which we choose the mean and standard deviation as the performance indicators.For the mean parameter with a significant change with time in the law，we establish regression modeling for longer storage stability parameter by RVM method，and carry out the performance prediction and calibration parameters compensation for the parameters stability of the shorter storage.The paper presents the modeling forecasting and parameter compensation for the long-term stability of the accelerometer scale factor of the important parameters in the inertial navigation system，the parameter stability mean performance for an interval time of 6 months has improved by 50.90%.This result implies that this method can replace the manual calibration and the use efficiency of inertial navigation systems，and verifies the effectiveness of the proposed method.

relevance vector machine；inertial navigation system；calibration cycle；long-term stability；predictive compensation

V241.6

A

0367-6234（2014）09-0015-04

2013-07-15.

國家重點基礎(chǔ)研究發(fā)展規(guī)劃資助項目（61388010404）.

黨宏濤（1976—），男，博士研究生；

王常虹（1961—），男，教授，博士生導(dǎo)師.

伊國興，ygx＠hit.edu.cn.