一種新的基于混合變換的圖像稀疏表示

石翠萍，張鈞萍，張 曄

（1.哈爾濱工業大學電子與信息工程學院，150001哈爾濱；2.齊齊哈爾大學通信與電子工程學院，161000黑龍江齊齊哈爾）

一種新的基于混合變換的圖像稀疏表示

石翠萍1，2，張鈞萍1，張 曄1

（1.哈爾濱工業大學電子與信息工程學院，150001哈爾濱；2.齊齊哈爾大學通信與電子工程學院，161000黑龍江齊齊哈爾）

Tetrolet變換對圖像中邊緣和紋理的稀疏逼近性能遠遠高于小波變換，對細節豐富的圖像具有明顯優勢，但其對平滑圖像的逼近性能卻不如小波變換.針對這一問題，本文提出了具有一定普適性的圖像稀疏方法.首先，對圖像進行小波變換，采用p-fold抽取濾波器對各子帶進行多相分解，對分解結果進行主成分變換，并對兩次能量聚集后的圖像進行低頻稀疏逼近；然后，根據前面結果生成細節圖像，采用Tetrolet變換進行高頻稀疏逼近.實驗表明，在相同條件下，無論是客觀質量還是主觀質量，該方法均優于單一的小波變換和Tetrolet變換，證實了本文方法的有效性.

圖像稀疏逼近；Tetrolet變換；小波變換；多相分解

圖像稀疏是以一種緊湊的形式來有效描述圖像的主要特征.圖像稀疏是圖像處理中的重要內容，是圖像特征提取、圖像壓縮、圖像增強等圖像處理技術的基礎.稀疏表示的前提是圖像能量應盡可能集中.傳統二維小波變換作為圖像稀疏的主要工具，得到廣泛的應用.然而，由于小波變換不能有效表示二維圖像中具有多方向性的邊緣和紋理等幾何特征，因此，多尺度幾何分析（multiscale geometric analysis，MGA）被提出，并迅速成為了研究熱點.其中，非自適應的小波有Curvelets［1］，Contourlets［2］，Directionlets［3］和Shearlets［4］，這些小波均具有更高的方向敏感性. Curvelets變換具有良好的時頻域局部性、方向性及非線性逼近能力.Contourlet變換具有隨尺度而變化長寬比的“長條”結構，用輪廓分割產生了更靈活、局部的圖像表示方法.Directionlets能對交叉直線提供最優逼近.Shearlets在頻域上是緊支撐的，具有較好的局部化特性.自適應的小波包括Bandlet變換［5］、wedgelet變換［6］等，可根據圖像局部結構來自適應調整基函數.2010年，Krommweh首次提出了Tetrolet變換［7］，該變換是一種局部自適應的Haar小波變換.由于支撐域非常小，因此不受Gibbs振蕩的影響，能更好地保持圖像邊緣和方向紋理信息［8］.Tetrolet變換一經提出，立即引起廣泛的關注和研究.然而，同其他稀疏方法一樣，Tetrolet變換也只針對具有某種特征的圖像才能體現出明顯優勢.對于包含明顯邊緣和紋理的圖像，利用Tetrolet變換進行稀疏逼近，則效果顯著.反之，若圖像較平滑，并不能體現較好的性能.本文利用Tetrolet變換對圖像細節保持較好這一特點，結合小波變換對平滑圖像的最優逼近這一性質，提出了一種新的圖像稀疏表示方法.

1 新的圖像稀疏表示方法總體框架

針對大多數稀疏逼近算法只對特定特征的圖像才具有最佳逼近性能，適應性差的特點，提出了一種具有一定通用性的稀疏逼近算法.該算法利用小波變換處理平滑圖像能力較強，以及Tetrolet變換對保留圖像邊緣和細節優勢明顯這兩大特點，將圖像的低頻部分和高頻部分分開處理.算法整體框架如圖1所示.

算法共分兩個階段.

第一階段:對圖像低頻進行稀疏逼近.

首先，對圖像進行小波變換.為了消除子帶內系數間的相關性，采用p-fold抽取濾波器對各子帶進行多相分解，并對分解后的分量進行主成分變換.這樣，圖像就相當于進行了兩次分解，因此能量更集中，可稀疏性更強.最后對這種能量高度集中的變換圖像保留較大的N1個系數，其余系數置0，即進行低頻稀疏逼近.根據稀疏逼近的結果，對上述過程進行反變換，得到原圖像的低頻圖像.

第二階段:對圖像高頻進行稀疏逼近.

將原圖像和第一階段得到低頻圖像相減，可得到包含絕大多數紋理和邊緣的高頻圖像.由于Tetrolet變換對細節的保持能力較好，故先對高頻圖像進行Tetrolet變換，然后保留較大的N2個系數，其余系數置0，即進行高頻稀疏逼近.對上述過程進行Tetrolet反變換，得到高頻圖像的近似.

最后，對兩次稀疏逼近的結果疊加，即可得到最終的重建圖像.

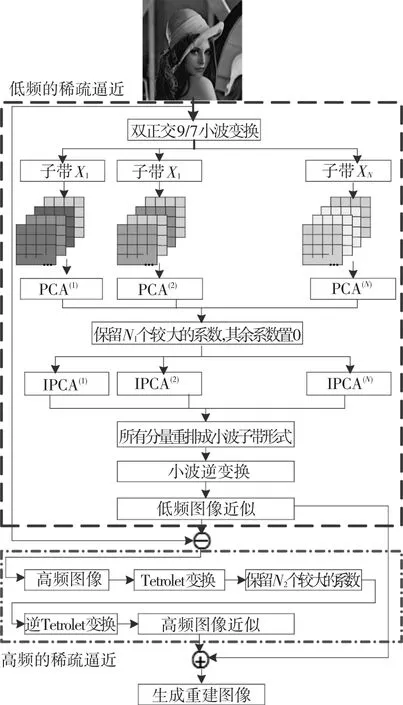
圖1 提出算法的總體框架

2 提出算法的具體實現

根據算法的總體框架，對給定的圖像，先進行小波變換并拆分子帶，然后進行PCA變換，對其進行稀疏表示得到低頻圖像.根據原圖像和低頻圖像，生成高頻圖像，再用Tetrolet變換對其進行稀疏逼近，得到高頻圖像的近似.下面從數學角度對該過程進行闡述.

2.1 基于小波變換和PCA的稀疏逼近

圖像經小波變換后，各子帶內的相鄰系數之間仍存在冗余［9］.如果能進一步去除這種冗余，則會增加圖像的能量聚集程度，使圖像的可稀疏性更強.算法流程圖見圖1的“低頻的稀疏逼近”部分，即算法的第一階段.

步驟1 用A表示小波變換，經L級小波變換后，小波圖像可以表示為

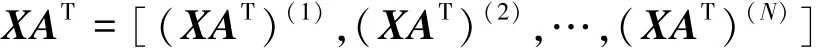
式中N表示小波子帶總數，為X為原圖像.

步驟2 對于每個小波子帶（XAT）（i），i=1，…，N，采用p-fold抽取濾波器對其進行多相分解，變為多個分量．從數學角度，可表示為

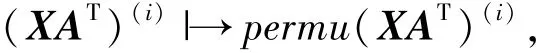
式中permu表示系數的重排．這里設p=4，即每個小波子帶被分為4個分量．下面以最低頻子帶LL1的分解為例，詳細給出小波子帶多相分解過程，如圖2所示.

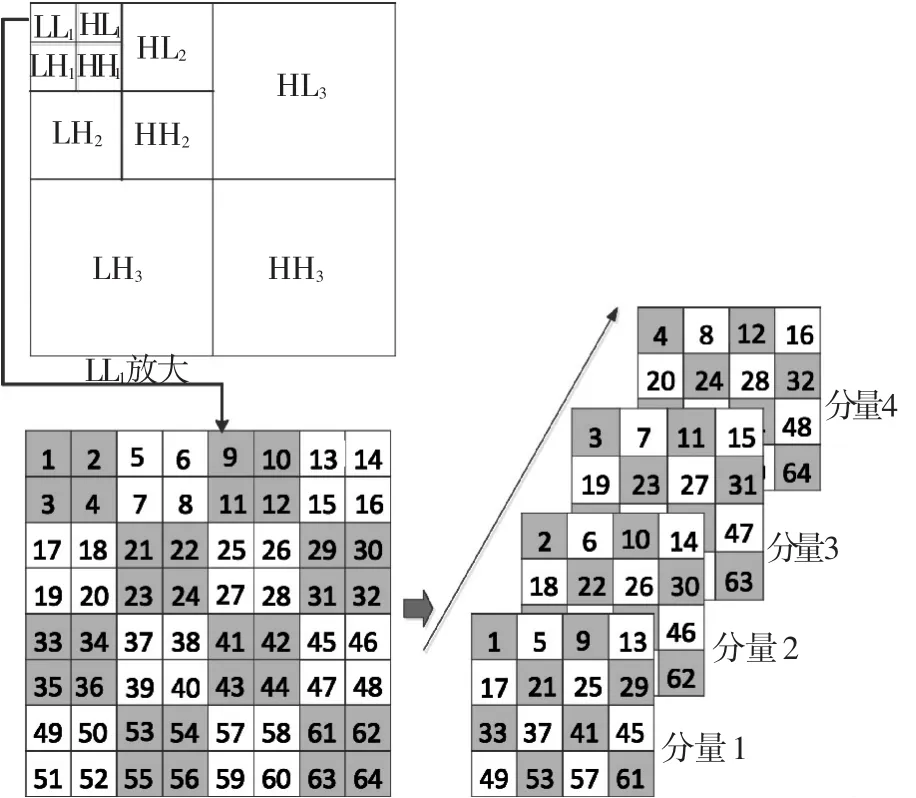
圖2 每個小波子帶多相分解的過程（以LL1為例）

設LL1的大小為8×8，為了消除相鄰系數間的冗余，將LL1劃分為若干個不重疊的塊，塊大小為2×2，為了視覺直觀，圖2中的塊用不同顏色表示.每個塊中的數字表示系數位置.用p-fold抽取濾波器對LL1多相分解:先抽取每個小塊中左上角的系數，并按對應塊的順序存放，組成第一個分量；同樣，抽取每個小塊中右上角的系數，并按對應塊的順序存放，組成第二個分量；依次類推，最后，抽取每個小塊中右下角系數，并按對應塊的順序存放，組成第4個分量.觀察圖2的4個分量，可以發現，每個塊中4個相鄰的系數剛好被放入各分量的相同位置，這樣，當對這些分量進行PCA時，即可實現每個塊內4個系數的能量再次集中，利用該特點即可去除相鄰系數間的冗余.其余子帶的分解過程和LL1的分解過程完全相同.

步驟3 對每個小波子帶生成的分量序列，計算對應的變換矩陣，并進行PCA變換，使能量更集中.設B（i）表示第i個子帶對應的PCA變換，則

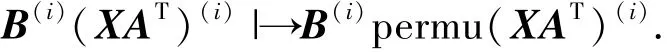
設經過上述小波變換和PCA變換后，圖像記作Y，可表示為

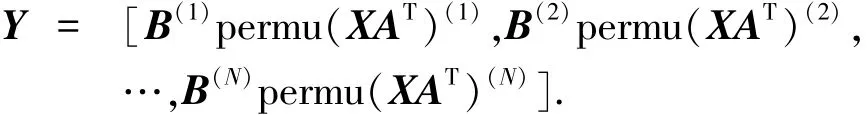
式中Y為經兩次能量聚集后的變換圖像．

步驟4 對Y進行稀疏逼近．將Y中所有分量序列的系數按絕對值從大到小排列，取出較大的N1個，其余系數置0，此時Y變為?Y，記作:

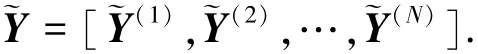
反變換過程如下:

步驟1 對?Y中每個子帶對應的分量序列進行PCA逆變換，記作B（i）-1，i=1，2，…，N，則全部分量序列經PCA逆變換后，可記為

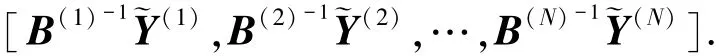
步驟2 根據上面的結果，將每個分量序列的內容重新組合，記作permu-1．完畢后，對整個變換圖像進行小波逆變換．設重建圖像為?X1，則:

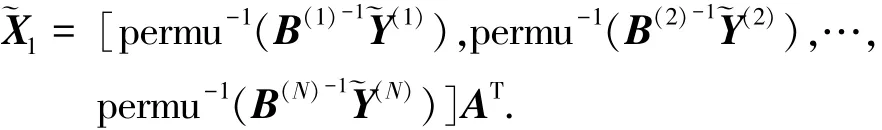
2.2 基于Tetrolet變換的稀疏逼近

Golomb提出了四格拼板（Tetrominoes）的概念.他指出，任何一副大小為N×N的圖像（N為偶數），都能由5個基本拼板組合而成，如圖3所示．

圖3 5種基本拼板

文獻［7］首次提出了Tetrolet變換，該變換的基本思想為:先將圖像分為若干個4×4的塊，每個塊都由4個基本四格拼板組成.四格拼板的選取原則是根據圖像塊的局部幾何特征，找到在四格拼板上定義的使得小波系數具有最小l1范數的拼板.對4×4的塊，共有117種拼板組合方案，若不考慮拼板的翻轉和旋轉，共有22種組合方案.

利用上述思想，對上面得到的高頻圖像X2，采用Tetrolet變換對其進行稀疏逼近，算法過程見圖1的“高頻的稀疏逼近”部分.

設輸入圖像X2，大小為M×M，即X2=（x［i，j］）．其中M=2K，K∈N．設J為Tetrolet變換分解層數，則在第r層，（r=1，…，J-1），進行自適應Tetrolet分解如下:

1）將圖像Xr2-1分成4×4的塊Qi，j，i，j=0，1，…，M／4r-1；

2）對每個塊，考慮117種允許的堆疊方法: c=1，…，117．對每一種堆疊方法，在4個四格拼板子集I，s=0，1，2，3上執行Harr小波變換，得到對應的4個低頻系數x和12個Tetrolet系數

式中

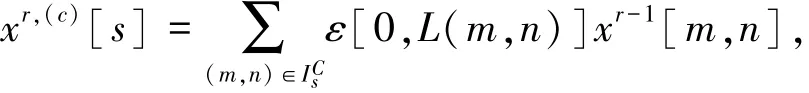
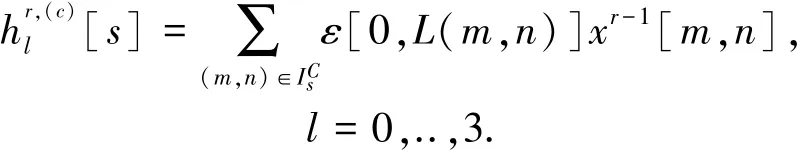
這里，ε［l，m］，l，m=0，…，3可從Harr小波變換矩陣得到．選擇最優的方向c?，使12個Tetrolet系數之和最小，此時選擇的模板為最優．

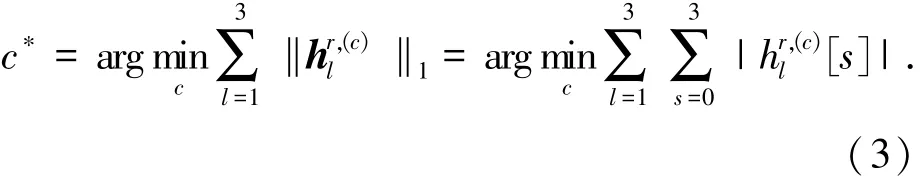
對每一個塊Qi，j，得到最優的Tetrolet分解

3）用變換矩陣R將低頻子帶和高頻子帶重排，大小為2×2的矩陣，以方便下一級變換．

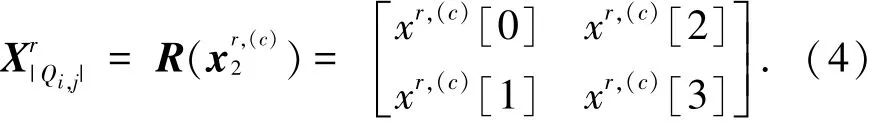
同樣

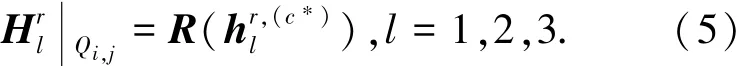
4）找到最優分解方向后，保存高頻部分系數及方向c?，對低頻圖像繼續進行Tetrolet分解，直至J-1層結束．

設Tetrolet變換后的圖像記為Y2，對Y2進行稀疏逼近．方法是將Y2中所有系數按絕對值從大到小排列，取出較大的N2個，其余系數置0，此時Y2變為．

反變換過程如下:

3 圖像特性分析及質量評估

設X和Y分別表示原始圖像和重建圖像，M和N分別表示圖像中行和列方向的像素數．先分析了圖像的特性，然后從客觀角度和主觀角度分別給出了評價圖像質量的指標．

3.1 圖像特性分析

圖像的空域性質可用空間頻率方法（spatial frequencymeasure，SFM）進行分析［10］.SFM定義如下:

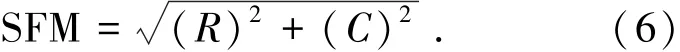
其中

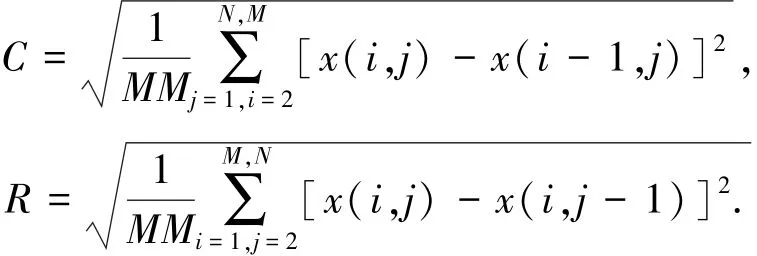
式中:R是行頻率，C是列頻率，x（i，j）表示原始圖像中的樣本．SFM表示圖像的整體頻率，也就是圖像的細節豐富程度.SFM越大，表示圖像細節越豐富.本文用SFM來分析細節對稀疏估計的影響.

3.2 質量評估測度

絕大多數文獻都采用PSNR來評估重建圖像的質量，然而，PSNR和MSE等客觀指標已被證實并不與人眼感知相一致［11-13］.因為實際中，有時具有較高PSNR的重建圖像，其視覺效果并不好.為了更好地評估所提算法，本文除采用PSNR作為客觀評估方法外，還采用SSIM［14］作為主觀評估方法，以綜合評定重建圖像的質量.

結構相似指標方法（structural similarity index measure，SSIM）可以用來衡量兩幅圖像的主觀相似度.其可由下式得:

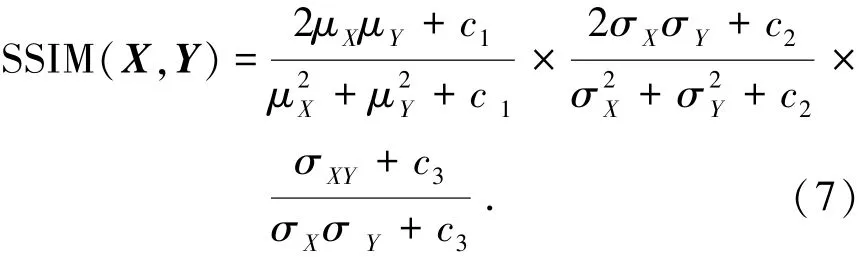
式中:X和Y分別表示原始圖像和重建圖像，μX和μY分別表示X和Y的均值，σX和σY分別表示X和Y的標準差，σXY表示X和Y的協方差．且c1=（k1L）2，c2=（k2L）2，c3=c2／2，k1=0.001，k2= 0.002（默認），L表示系數的動態范圍．

最終得到的SSIM的范圍為［-1，1］，值越大，表示重建圖像在視覺上越逼近原始圖像.當值為1時，表示重建圖像和原始圖像完全一致.

4 實驗及結果分析

為驗證本文方法的有效性，采用一些測試圖像進行了實驗，并在相同條件下，與小波變換和Tetrolet變換方法進行了比較.

實驗中小波變換和Tetrolet變換的分解級數均為3級，采用的小波為cdf9／7小波，測試圖像大小均為256×256.在本文方法中，設低頻的稀疏逼近中保留系數個數為N1個，高頻的稀疏逼近中保留個數為N2個，與小波變換和Tetrolet變換后直接保留N1+N2個系數進行對比．為了充分驗證算法，采用兩組不同的N1和N2進行實驗:分別是N1=6 000，N2=2 000和N1=8 000，N2=3 000．

下面對Lena圖像進行實驗，實驗結果及局部放大圖如圖4所示.圖4（b）～（d）是在N1= 6 000，N2=2 000的條件下，分別采用Tetrolet變換、小波變換和本文算法得到結果的局部放大圖.可以看到，相比于其它兩種方法，本文方法能夠更好的保留圖像細節.從整個重建圖像質量上看，采用Tetrolet變換、小波變換和本文算法得到的PSNR分別為33.44、35.09和35.58 dB，進一步證明了本文方法的優越性.

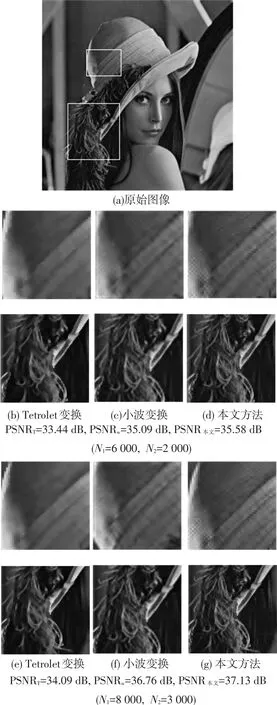
圖4 不同實驗條件及方法下重建圖像質量及局部放大

從算法角度分析該原因，本文方法在低頻估計階段采用PCA進行了相鄰系數去冗余，加上小波變換，相當于進行了兩次能量集中，故在保留相同個數系數的條件下，本文方法的系數包含的能量更多，故低頻重建的質量更好.另一方面，低頻能量高度集中的結果，使得原圖像的細節信息盡可能多的保留在高頻圖像中.采用Tetrolet變換對該高頻圖像進行稀疏表示，則發揮了Tetrolet變換能夠較好的逼近圖像邊緣和紋理信息的優勢.結合不同變換的特點，以及圖像低頻和高頻信息不同這一事實，對圖像分開處理，這就是本文方法效果較好的原因.

圖4（e）～（g）是在N1=8 000，N2=3 000的條件下得到的結果，與圖4（b）～（d）得到的結果有相同的規律.

不失一般性，采用一組常用的自然圖像作為測試圖像，如圖5所示.先分析圖像特性，然后分別從主觀角度和客觀角度去衡量本文算法結果.

圖5 8幅用于測試的圖像

對于每幅測試圖像，先根據式（6），計算對應的空間頻率特性，結果見表1.

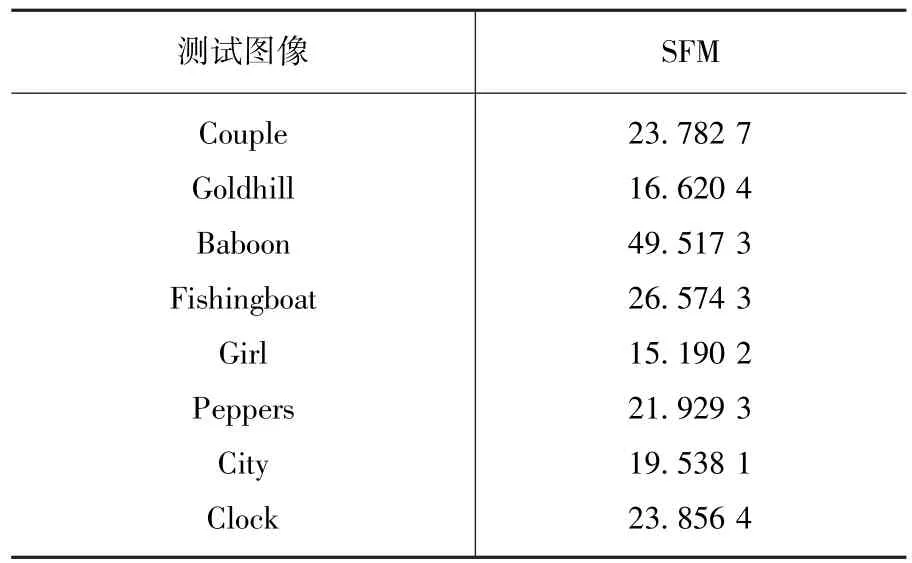
表1 測試圖像對應的SFM

在不同的實驗條件下（不同的N1和N2），對圖5中的每幅測試圖像，分別采用本文算法、Tetrolet變換和小波變換，并用PSNR和SSIM來評價圖像的客觀質量和主觀質量，結果見表2.

為了更直觀地對比表2的結果，以N1= 8 000，N2=3 000的情況為例，繪制PSNR和SSIM的曲線，結果如圖6和圖7所示.

從圖6可以看出，對于給定的測試圖像，本文方法得到的PSNR均高于其他兩種單一的變換方法.其中，對于圖像Baboon，PSNR增加的幅度很小，其原因可以從圖像特性分析得到.根據表1的結果，在所有測試圖像中，圖像Baboon的SFM值最大，而且高出其他圖像SFM值很多，說明該圖像包含的高頻成分特別多，換句話說，該圖像的細節特別豐富.在這種情況下，對于文中提出的將圖像低頻和高頻分別處理，且保留的低頻系數個數多于高頻系數個數的方法，沒有明顯優勢.盡管如此，對于Baboon圖像，采用本文方法的PSNR依然優于采用Tetrolet變換的結果，只是程度不同而已.同樣，在圖7中，從人眼的視覺角度出發，從主觀上衡量重建圖像的質量.結果表明，本文方法得到的結果在視覺上仍然優于其他兩種變換方法.該實驗充分證明了本文方法的有效性.在N1=6 000，N2=2 000時，也有相同的規律，這里不再給出圖示.

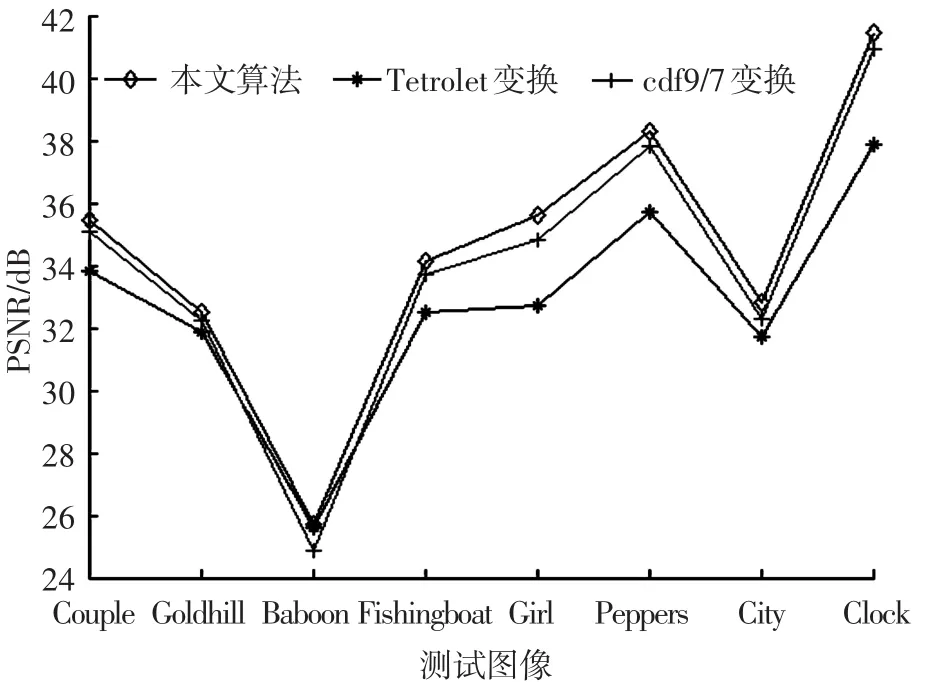
圖6 N1=8 000，N2=3 000條件下PSNR對比

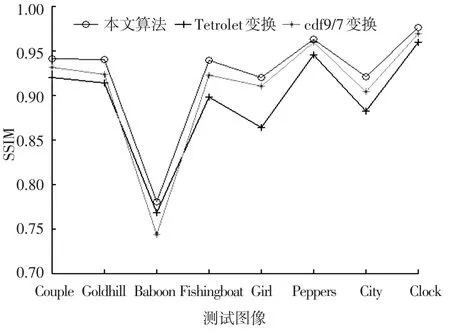
圖7 N1=8 000，N2=3 000條件下SSIM對比

表2 對于給定測試圖像，不同實驗條件下的實驗結果對比

5 結 語

針對現有絕大多數圖像稀疏逼近算法通用性不強，僅對具有特定特征的圖像才有較好逼近效果的問題，結合Tetrolet變換和小波變換各自優點，本文提出了一種新的具有一定普適性的圖像稀疏方法.該方法同時利用了小波變換對平滑圖像的最優逼近，以及Tetrolet變換對圖像細節保持較好這兩大特點，將兩者分別用在圖像的低頻和高頻處理中.實驗證明，在相同條件下，無論是主觀質量還是客觀質量，采用本文方法得到的重建圖像均好于單一變換得到的結果.本文方法能夠在較好的保持圖像低頻信息同時，盡可能保留圖像的主要細節.該稀疏方法為壓縮提供了有效的預處理，下一步擬將圖像稀疏與特定的壓縮方法結合，期望得到較好的壓縮效果.

［1］CANDES E J，DONOHO D L.New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities［J］.Communications on Pure and Applied Mathematics，2004，57（2）:219-266.

［2］DO M N，VETTERLIM.The contourlet transform:an efficient directionalmultiresolution image representation［J］.IEEE Transactions on Image Processing，2005，14（12）:2091-2106.

［3］FRIEDRICH F，DEMARET L，FüHR H，etal.Efficient moment computation over polygonal domains with an application to rapid wedgelet approximation［J］.SIAM Journal on Scientific Computing，2007，29（2）:842-863.

［4］GUO K H，LABATED.Optimally sparsemultidimensional representation using shearlets［J］.SIAM Journal on Mathematical Analysis，2007，39（1）:298-318.

［5］PENNEC E L，MALLAT S.Sparse geometric image representationswith bandelets［J］.IEEE Transaction on Image Processing，2005，14（4）:423-438.

［6］DONOHO D L.Wedgelets:Nearlyminimax estimation of edges［J］.Annals of Statistics，1999，27（3）:859-897.

［7］KROMMWEH J.Tetrolet transform:A new adaptive Haar wavelet algorithm for sparse image representation［J］.Journal of Visual Communication and Image Representation，2010，21（4）:364-374.

［8］KROMMWEH J，MA Jianwei.Tetrolet shrinkage with anisotropic total variation minimization for image approximation［J］.Signal Processing，2010，90（8）: 2529-2539.

［9］LIU Juan，MOULIN P.Information-theoretic analysis of interscale and intrascale dependencies between image wavelet coefficients［J］.IEEE Transactions on Image Processing，2001，10（11）:1647-1658.

［10］ESKICIOGLU A M，FISHER P S.Image quality measures and their performance［J］.IEEE Transactions on Communications，1995，43（12）:2959-2965.

［11］YOU Junyong，EBRAHIMI T，PERKIS A.Attention driven foveated video quality assessment［J］.IEEE Transactions on Image Processing，2014，23（1）:200-213.

［12］穆為磊，高建民，王昭，等.考慮人眼視覺特性的射線檢測數字圖像質量評價方法［J］.西安交通大學學報，2013，47（7）:91-95.

［13］ZHANG Yongfei，CAO Haiheng，JIANG Hongxu，etal. Visual distortion sensitivity modeling for spatially adaptive quantization in remote sensing image compression［J］.IEEE Transactions on Geoscience and Remote Sensing Letters，2014，11（4）:723-727.

［14］WANG Zhou，BOVIK A C，SHEIKH H R，etal.Image quality assessment:from error visibility to structural similarity［J］.IEEE Transactions on Image Processing，2004，13（4）:600-612.

（編輯苗秀芝）

A novel image sparse representation based on the hybrid transform

SHICuiping1，2，ZHANG Junping1，ZHANG Ye1
（1.School of Electronic and Information Engineering，Harbin Institute of Technology，150001 Harbin，China；2.School of Communication and Electronic Engineering，161000 Qiqihaer，Heilongjiang，China）

The sparse approximation performance of tetrolet transform to the edge and texture of image ismuch higher than wavelet transform，which makes it suitable for those images that rich in details.However，for the smooth images，its sparse approximation performance isweaker than wavelet transform.Focus on the problem，a novel sparse approximation method that is of some generality is proposed.First，the wavelet transform is conducted to the image，and the polyphase decomposition for each sub-band is operated using p-fold filter and some components are generated，then the PCA is applied to those components.Following，the sparse approximation is conducted to the image after two energy concentration.Secondly，the high-frequency image can be obtained based on the results above，then the tetrolet transform is applied to sparse it.Experimental result shows that，under the same condition，the quality of the reconstructed image obtained by the proposed method is better than that obtained by the wavelet transform and the tetrolet transform，either the subjective or objective quality，which indicates the effectiveness of the proposed method.

image sparse approximation；tetrolet transform；wavelet transform；polyphase decomposition；

TP751.1

A

0367-6234（2014）09-0036-07

2013-09-30.

國家自然科學基金資助項目（61271348）；黑龍江省教育廳資助項目（12521614）；齊齊哈爾大學青年教師科研啟動項目（2011k-M11）.

石翠萍（1980—），女，博士研究生；張鈞萍（1970—），女，教授，博士生導師；張 曄（1960—），男，教授，博士生導師.

張鈞萍，zhangjp＠hit.edu.cn.