橢球、七參數與四參數同時解算方法研究與應用

鄒俊平

(上海市測繪院,上海 200063)

橢球、七參數與四參數同時解算方法研究與應用

鄒俊平?

(上海市測繪院,上海 200063)

測量應用中,常常需要將RTK獲取的三維空間坐標轉換成當地高斯平面坐標和高程。一般的轉換方法是采用空間七參數或平面四參數轉換模型。因此為了實時獲取當地坐標,需要預先求取相應的轉換參數,這些參數包括橢球長半軸、橢球扁率和空間七參數或者平面四參數。本文研究實現了一種同時解算這13個參數的數學模型,可根據具體應用需要進行自由求取。并以上海地區為例,解算了8種參數組合,分析比較了不同參數對坐標轉換結果的影響。

坐標轉換;數據處理;空間七參數;平面四參數;地方坐標

1 前 言

RTK測量獲得的WGS84坐標通常需要轉換成地方平面坐標和高程,以用于生產。為了實現地方平面坐標和高程的實時獲取,需要預先求得相應的轉換參數并設置在RTK流動站設備中。根據RTK流動設備的不同,這些參數可能包括橢球長半軸,橢球扁率,用于笛卡兒坐標空間轉換的七參數或者平面坐標轉換中采用的四參數。目前絕大多數RTK流動站設備都支持上述幾類參數組合。

一般的做法是將橢球長半軸、橢球扁率設置為當地投影橢球的參數,在此基礎上根據RTK流動設備的參數設置需要,可將測量獲得的大地坐標轉換成笛卡爾空間坐標并求取與當地坐標的空間轉換七參數或者進行高斯投影后在平面上求取與當地坐標的平面轉換四參數。然而,這兩套參數往往不能同時求取,并且同一套參數可能不適用于所有的RTK流動站設備。另外,采用七參數模式時,7個參數之間存在群相關,當區域較小時,求解七參數可能失敗。采用四參數模式時,地圖投影變形的差異將不能估計,區域越大,誤差越大。采用不同的轉換參數,對結果的影響可達1 cm。

本文設計了同時解算此類轉換參數的統一模型,在這個模型中可同時解算包括橢球長半徑、橢球扁率、空間轉換七參數、平面轉換四參數在內的13個參數,也可根據具體需要單獨解算部分參數以解決RTK流動站設備轉換參數設置差異的問題。本文以上海地區為例,分析各種參數組合對結果的影響。另外,該模型亦可用于區域最佳橢球投影面的求取。

2 坐標轉換的數學模型

RTK測得的大地坐標轉換為地方平面坐標和高程的過程如下:

2.1 大地坐標換算至空間坐標

如果RTK測得的WGS84的大地坐標為(B L H)T,那么其空間坐標(X Y Z)T可由下式算得:

其中a為橢球長半軸,f為橢球扁率。

2.2 七參數轉換

通過七參數轉換模型將(X Y Z)T轉換成當地坐標框架下的空間坐標(X′ Y′ Z′)T,

上式中的(X0Y0Z0)T為空間平移量,k為空間尺度因子,αx、αy、αz為3個坐標軸的旋轉角。

2.3 新的大地坐標與投影坐標

由式(1)的逆形式將當地坐標框架下的空間坐標(X′Y′ Z′)T化算為大地坐標(B′ L′ h′)T,然后通過高斯投影獲得當地坐標框架的平面坐標(xg′ yg′)T。

2.4 求地方坐標

地方坐標與高斯投影后獲得的平面坐標往往還存在一定差異,還需采用平面四參數模型建立二者的關系:

上式中的(x0y0)T為平面平移量,k1為平面尺度因子,α為平面旋轉角。

由(xg′ yg′)T求(xgyg)T的反算公式為:

3 全參數求解數學模型

以上計算流程表示為關系式:

上式函數f()代表前面從WGS84大地坐標(B L H)T轉換為當地平面坐標(xgygh′)T的整個過程。式(5)中總共包含13個參數。

為求解這13個參數,將式(5)進行線性化,可寫成誤差方程:

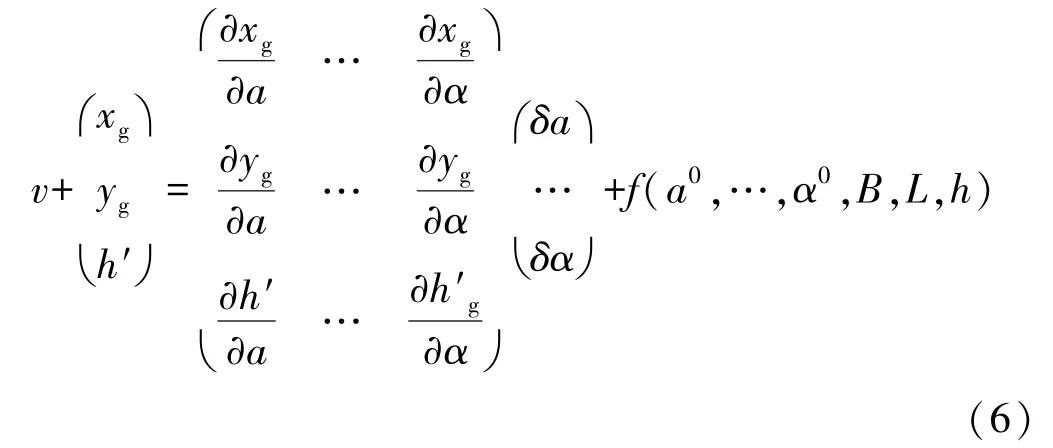
上式中的系數陣可采用數值導數方法求得[6],組成法方程迭代至收斂即可解得所有參數。由于某些參數在計算中起的作用相同或相近,因此13個參數不能同時解算,例如a與k完全相關,a與k1相關性很大[5]。

4 算 例

以上海地區為例,表1為選取測試區域的經緯度范圍。

表1 上海地區經緯度范圍

在上海地區建有9個CORS站,并有一個IGS站(SHAO),這10個點既有大地坐標又有當地平面坐標和高程。由10個公共點,按不同方案計算轉換參數,各方案解算的參數如表2所示。

轉換殘差是衡量轉換參數的主要標準之一,下表3是方案1的轉換殘差,各個解算方案的殘差中誤差列于表2中。

表2 轉換參數計算方案

表3 方案1的轉換殘差

為了評價不同轉換參數對上海地區坐標轉換結果的影響,將上海地區按10′×10′劃分格網,將各格網點的經緯度轉換至地方坐標,不同轉換參數求得的平面坐標和高程不相同,表4列出了各解算方案與方案1轉換坐標的點位差。

表4 轉換結果與方案1的點位差

將各方案解算得到的格網點坐標與方案1相比,差異如圖1、圖2所示:

圖1 方案2算得坐標與方案1算得坐標點位差(單位/m)

圖2 方案3-8算得坐標與方案1算得坐標點位差(單位/m)

為評價目前RTK流動站主要采取的坐標轉換方式在上海區域的差異,選取方案2和方案3與方案1相比坐標差結果,結合上海地區的區域分布,獲得上海地區坐標轉換點位差異分布,如圖3、圖4所示。

圖3 方案2算得坐標與方案1算得坐標點位差在上海地區的分布(單位/mm)

圖4 方案3算得坐標與方案1算得坐標點位差在上海地區的分布(單位/mm)

方案2與方案1的區別在于是否將橢球扁率作為未知參數進行求解,方案3與方案1的區別其實是常用的坐標轉換四參數模型與七參數模型的區別。從算例分析,因橢球扁率的變化必然引起高斯平面坐標的顯著變化,雖然依據各坐標轉換參數之間存在一定的相關性能對不同參數造成的影響進行修正,但對應于顯著性的變化很難進行平滑擬合。因此,圖3呈現出沿高斯投影中央子午線成對稱趨勢,該差異主要是高斯投影差異的體現。而將高斯投影參數固定后的方案3和方案1相比,因為采用同樣的高斯投影參數,故而在上海這樣的小范圍區域,該差異僅體現為空間坐標與高斯平面坐標的轉換精度誤差。

5 結 論

本文介紹了RTK構建橢球參數、七參數與四參數同時解算的數學模型和解算方法。該方法可用于不同RTK流動站軟件的不同參數設置。

以上海地區為例,解算了八種參數組合,并采用實際數據進行了比較,從坐標差異性的分布來看存在東西對稱的分布特點,就上海區域而言平面四參數模型與空間七參數模型差異不明顯,其余各種參數組合對點位結果的影響可達厘米級。該方法對于建立城市獨立坐標系統與國家CGCS2000的轉換關系具有現實意義。考慮到GNSS應用的逐漸深入,涉及高程的七參數模型在RTK、似大地水準面精化模型應用更具有實際意義。通過本文算例分析,在上海地區求取上海獨立坐標系與CGCS2000的坐標轉換關系可采用方案1 (七參數模型)。

[1] 施一民.現代大地控制測量[M].上海:同濟大學出版社,2003.

[2] 武漢測繪科技大學控制測量教研室,同濟大學大地測量教研室合編.控制測量學(下)[M].北京:測繪出版社, 1992.

[3] 朱華統,楊元喜,呂志平.GPS坐標系統的變換[M].北京:測繪出版社,1994.

[4] 王解先,王軍,陸彩萍.WGS84與北京54坐標的轉換問題[J].大地測量與地球動力學,2003,23(3):70～73.

[5] 王解先.七參數轉換中參數之間的相關性[J].大地測量與地球動力學,2007,27(2):43～46.

[6] 王解先,徐志京.三種坐標間轉換的雅可比矩陣數值導數計算方法[J].大地測量與地球動力學,2004(11):P19～23.

[7] 劉大杰,施一民,過靜珺.全球定位系統(GPS)的原理與數據處理[M].上海:同濟大學出版社,1996.

[8] 李征航,黃勁松.GPS測量與數據處理[M].武漢:武漢大學出版社,2005.

Determine Earth Ellipsoid Together With Seven and Four Transformation Parameters

Zou Junping
(Shanghai Municipal Institute of Surveying and Mapping,Shanghai 200063,China)

In surveying applications,the positioning results obtained from GPS RTK are usually presented in local plane coordinate and height respectively.Some pre-setting parameters including the semimajor axis,oblateness of the earth ellipsoid,cartesian seven-parameters of transformation,and four-parameters for plane coordinate transformation are needed.In this paper,a method to solve all these 13 parameters in one model is introduced.Eight groups of parameter combination are solved for Shanghai area and the differences of results were compared.

coordinate transformation;data processing;seven-parameters of transformation;four-parameters for plane coordinate transformation;Local coordinates

2014—05—06

鄒俊平(1982—),男,工程師,從事精密工程測量與GNSS應用研究。