基于最小二乘估計的聲矢量陣穩健波束形成

王燕,吳文峰,梁國龍

(哈爾濱工程大學水聲技術重點實驗室,黑龍江哈爾濱 150001）

基于最小二乘估計的聲矢量陣穩健波束形成

王燕,吳文峰,梁國龍

(哈爾濱工程大學水聲技術重點實驗室,黑龍江哈爾濱 150001）

針對存在導向矢量失配和快拍數不足時,聲矢量陣標準Capon波束形成器性能急劇下降的問題,提出了一種基于最小二乘估計的聲矢量陣穩健波束形成算法。鑒于聲矢量陣聲壓通道和振速通道的導向矢量誤差來源不同,分別為聲矢量陣聲壓通道和振速通道設計了廣義旁瓣對消器;利用最差性能最優化的思想,將聲矢量陣標準Capon波束形成器轉化為穩健最小二乘估計問題;利用二階錐規劃求解。仿真分析表明,該算法在抗導向矢量失配、快拍數不足、陣元姿態誤差方面均有良好的性能。

信息處理技術;穩健自適應波束形成;聲矢量陣;廣義旁瓣對消器;最小二乘估計

0 引言

矢量傳感器可以同點輸出聲場的聲壓和振速信息,相比于標量陣,基于矢量傳感器的陣列不僅在目標方位估計方面有獨特的優勢,而且能獲得更高的空間增益[1]。由于矢量傳感器在構造和信號處理方式上的復雜性,矢量陣的自適應信號處理方法受導向矢量失配和快拍數不足的影響更為嚴重[2]。如矢量陣標準Capon波束形成(SCBV)在理想情況下是最優處理器,但在實際應用中,除了陣元幅相誤差、位置誤差、陣元間的互耦等失配外,各陣元的姿態誤差同樣會引起SCBV性能的下降[3],甚至導致期望信號自消現象。

對角加載技術是提升自適應波束形成算法穩健性常用的方法[4-6],該方法主要的缺點是最優對角加載量難以確定。Zhang等將基于廣義協方差矩陣擬合(GLCV)方法應用于矢量陣[7],該方法在快拍數不足時具有較高的穩健性,但并未充分考慮導向矢量誤差的影響。文獻[8]將穩健波束形成方法移植到矢量陣上,并通過對聲壓通道和振速通道設定不同的導向矢量不確定集,提出了矢量陣穩健波束形成(RCBV),該算法的性能受導向矢量不確定集估計精度的影響。文獻[9]同樣區別對待聲壓和振速分量,通過對二者的權向量賦予不同范數約束,提出了基于雙重范數約束的矢量陣波束形成(DNCV),該方法能靈活處理聲壓和振速的穩健性,但在抗陣元姿態誤差方面仍存在不足。

針對存在導向矢量失配和快拍數不足時,聲矢量陣標準Capon波束形成器性能下降問題,提出了一種基于聲矢量陣最小二乘(LSV)估計的穩健波束形成算法。該算法通過若干個廣義旁瓣對消器抵消聲壓通道和各振速分量干擾,在抑制干擾的同時,還能獲得足夠的穩健性。如無特殊說明,矩陣的范數均指F范數。

1 聲矢量陣穩健波束形成

二維聲矢量傳感器能同時拾取聲場中同一點的振速xvx、xvy和聲壓xp.對θ方向入射的遠場平面波,單矢量傳感器的時域輸出為

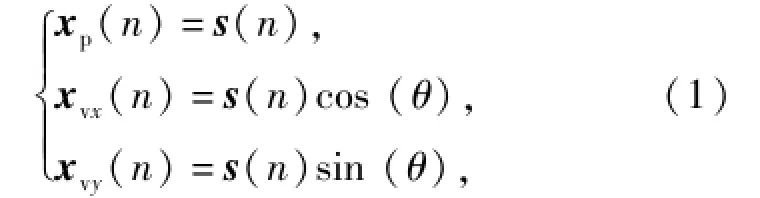
式中:s(n)為傳感器接收的聲壓波形,n為快拍數序號,為了分析方便假設波阻抗為1,這并不影響問題的分析。考慮一個M元二維聲矢量陣列,K(K＜M)組獨立遠場窄帶平面波從θk(k=1,…,K)方向入射到基陣,則矢量陣輸出模型可以表示為

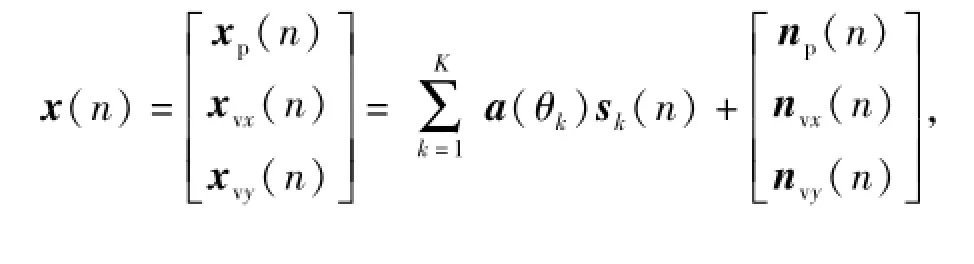
式中:wd=[,]T,wp和wv分別為聲壓通道和振速通道的加權向量;ξ1和ξ2為用戶設定值,其值越小,波束形成器穩健性越高,但陣增益會隨之下降,通過對兩參數選取合適的值,可使DNCV波束形成器在高增益和高穩健性之間折中。

2 基于LSV估計的穩健波束形成算法

2.1 算法描述

廣義旁瓣對消器將波束形成器的權向量分解為靜態權向量和自適應權向量兩個部分[11],其中自適應權向量由阻塞矩陣和對應系數組成。利用該思想可為矢量陣各通道設計廣義旁瓣對消器,若將矢量陣常規波束形成器的權值作為靜態權值,則(3)式中的權向量可以表示為

圖1中,ηp、ηx、ηy∈CM-1分別為聲壓、x軸和y軸對應阻塞矩陣的系數向量,在此結構下(5)式中的阻塞矩陣為B=I3×3?Q,相應系數為η=[p]T.將(5)式代入(3)式,并注意到wHs=1自然滿足,則(3)式所述優化問題變為

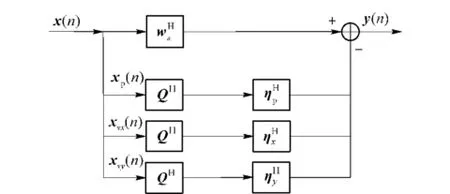
圖1 聲矢量陣廣義旁瓣對消結構Fig.1 Generalized sidelobe cancellers of vector-sensor array

由于利用有限快拍估計的Rx和實際數據協方差矩陣Rx之間存在誤差,導致A和b均存在誤差ΔA和Δb,則有

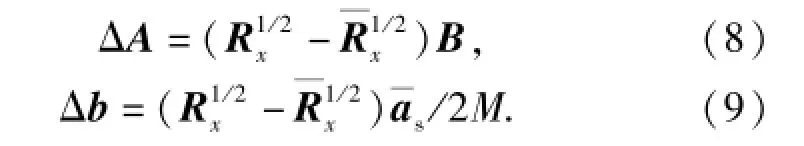
LSV估計對上述誤差極為敏感,在考慮存在誤差情況下,(7)式更為精確的表達式為

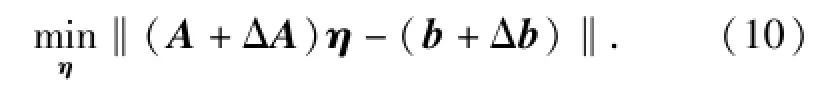
令ρ表示最差情況下‖[ΔA Δb]‖的取值,即‖[ΔA Δb]‖≤ρ,對每次批處理ρ為常數,關于ρ的取值將在下小節介紹。由最差性能最優化的思想,(7)式所述LSV估計轉化為如下穩健LSV估計:

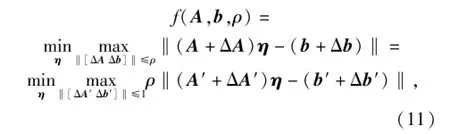
式中:A′=A/ρ;b′=b/ρ;ΔA′=ΔA/ρ;Δb′=Δb/ρ.由于ρ為常數,并不影響(11)式最后一項的解,先考慮最差情況下,即‖[ΔA′Δb′]‖=1時的如下問題:

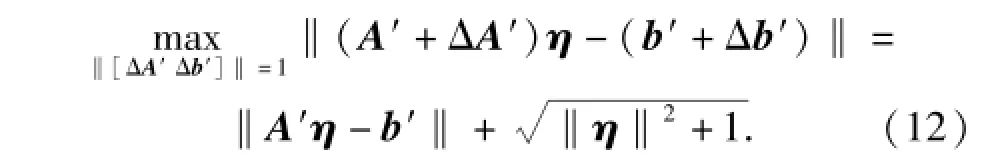
(12)式成立的條件是兩向量A′η-b′和ΔA′η-Δb′同相,即

(14)式可以通過高效內點法求解[12],求解得η后利用(5)式即可計算最終權值。

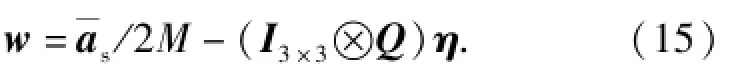
值得注意的是,上述推導過程是利用聲矢量陣常規波束形成權值作為LSV算法的靜態權值得出,但這并不妨礙其他一些算法權值作為本文算法的靜態權值,如線性約束最小方差波束形成器[13](LCMV),只是此時的阻塞矩陣變為和LCMV算法約束子空間正交的正交子空間,除此之外,其余推導過程一樣適用,篇幅所限本文將不再展開敘述。

2.2 參數計算

假設實際數據協方差矩陣Rx和估計數據協方差矩陣間存在誤差矩陣Δ,且滿足

式中:γ在每次批處理中為常數。在誤差矩陣的范數約束下,(3)式可以表示為

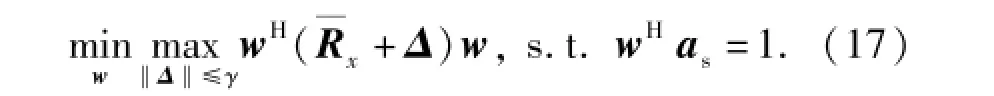
為了計算最差情況下的數據協方差矩陣,先考慮如下問題:

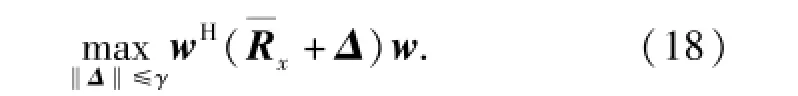
利用Lagrange乘子法可得(18)式的解[14]

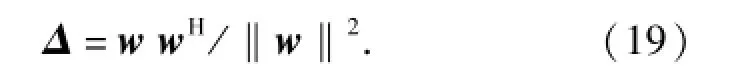
將(19)式和(18)式帶入(17)式可得

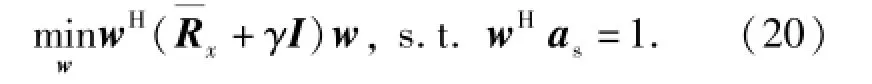
由(20)式可以看出,在誤差矩陣的范數約束下,最差情況下的數據協方差矩陣為+γI,利用(20)式替代Rx并代入(8)式和(9)式,可得ρ的取值:

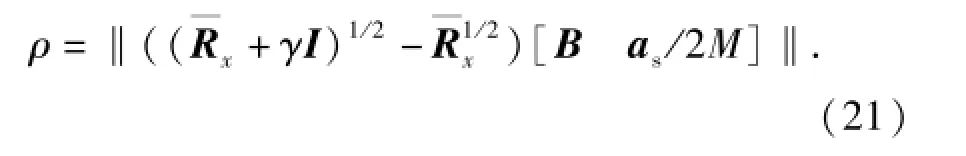
由于γ值會隨信號和干擾的功率變化而變化[15-16],為了消除這種不確定性,引入參數γ0,使其滿足

式中:tr(·)表示取矩陣的跡;γ0是本文算法唯一引入的參數,用于評價數據協方差矩陣的估計誤差,一般選擇在0.5～1之間即可。為了提高小快拍時的估計精度,可利用GLCV算法對其預處理。

3 計算結果與比較

為驗證LSV算法的穩健性及求解的正確性,設計了如下仿真實驗。考慮一個由5元聲矢量傳感器組成的均勻線陣,陣元間距為半波長。定義陣列舷側方向為0°,理想情況下各陣元y軸和線陣重合。3組平面波分別從10°、-30°和35°方向入射到基陣,其中10°方向的信號為期望信號,其他兩組為干擾,且干噪比分別為15 dB和20 dB,信號和干擾均為互不相關的隨機窄帶過程。聲壓通道和矢量各軸噪聲均為0 dB空間白噪聲。將本文方法和現存4種方法(SCBV、GLCV、RCBV和DNCV)進行了比較分析,其中本文算法中的參數γ0=0.5,DNCV的參數取文獻[8]的參考值ξ1=0.08和ξ2=0.06,由于RCBV參數取值和導向矢量不確定集有關,因此根據不同情況取各通道導向矢量不確定集上限的期望值,所有實驗結果均是200次Monte Carle實驗取平均值的結果,為了比較分析圖中也給出了最優情況下的性能。

3.1 對隨機導向矢量誤差穩健性對比

隨機導向矢量誤差指由各陣元幅相誤差和陣元位置誤差引起的導向矢量誤差,假設真實導向矢量as和預設導向矢量存在隨機誤差,即as=+e,其中e為服從均值為0、協方差矩陣為σ2I的復高斯隨機變量[17],快拍數取100.圖2顯示σ=0.1時,各算法輸出信干噪比SINR隨輸入信噪比SNR變化曲線。圖3顯示期望信號信噪比為10 dB時,各算法輸出信干噪比隨導向矢量誤差的標準差σ變化曲線,橫軸用標準差對數20lgσ表示。從圖2可以看出,RCBV算法性能和DNCV算法性能相當,在整個考慮的輸入信噪比范圍內,本文算法的性能均高于其他算法。從圖3可以看出,在導向矢量誤差標準差小于-18 dB,RCBV算法、DNCV算法和本文算法性能幾乎沒有變化。隨導向矢量誤差標準差繼續增加,各算法性能均出現一定下降,但本文算法的性能均略高于其他算法。

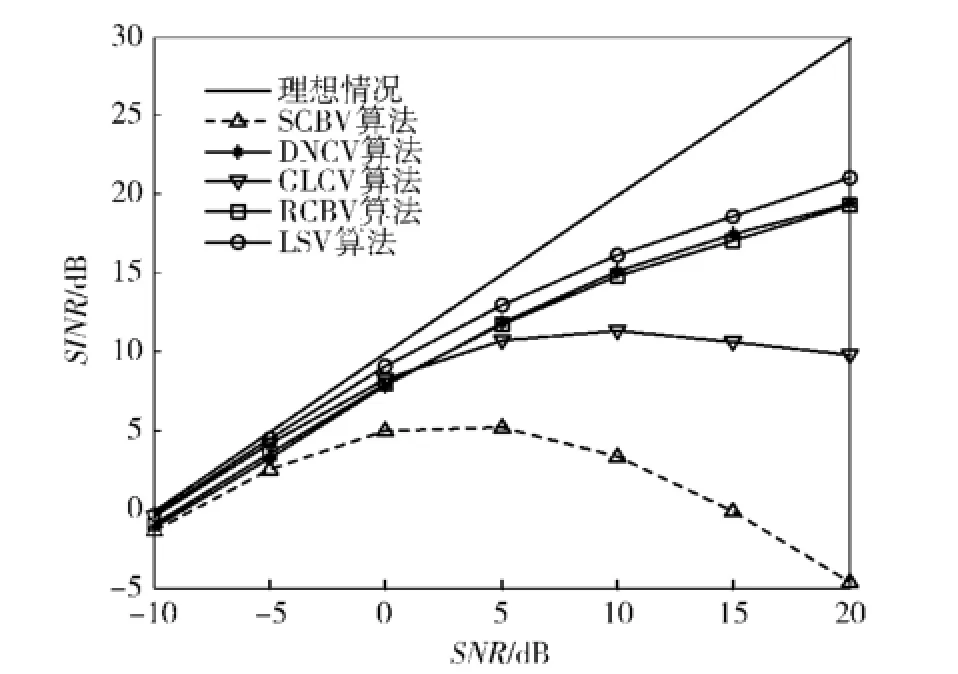
圖2 各算法輸出信干噪比隨輸入信噪比變化曲線Fig.2 Output SINR versus input SNR

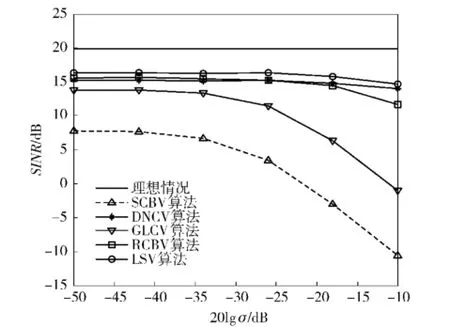
圖3 各算法性能隨導向矢量誤差的標準差變化曲線Fig.3 Output SINR versus standard deviation of steering vector error

3.2 對觀測方向誤差穩健性對比

考慮精確校準的陣列,即不存在3.1節中的隨機誤差,由于波束掃描間隔的限制,波束預成方向和期望信號實際入射方向不可避免存在誤差,令該方位誤差為Δθ.圖4顯示Δθ=1°時,各算法輸出信干噪比隨輸入信噪比變化曲線,快拍數取100.圖5顯示期望信號信噪比為10 dB時,各算法輸出信干噪比隨觀測方向誤差變化曲線,快拍數取100.從圖4可以看出在輸入信噪比小于15 dB時,本文算法的性能均高于其他算法,當輸入信噪比繼續升高時, RCBV算法的性能逐漸和本文算法性能接近,輸入信噪比為20 dB時,二者性能相當。從圖5可以看出,SCBV算法和GLCV算法對觀測方向誤差極為敏感,在整個誤差區間內,本文算法、RCBV算法和DNCV算法表現都比較穩定。不存在觀測方向誤差時,各算法性能較最優值低是由快拍數不足引起的。

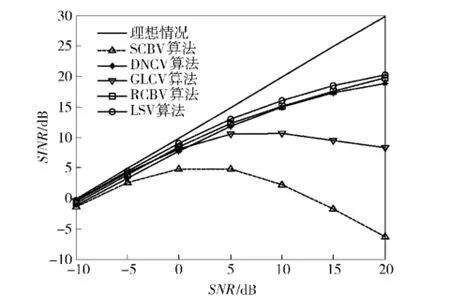
圖4 各算法輸出信干噪比隨輸入信噪比變化曲線Fig.4 Output SINR versus input SNR

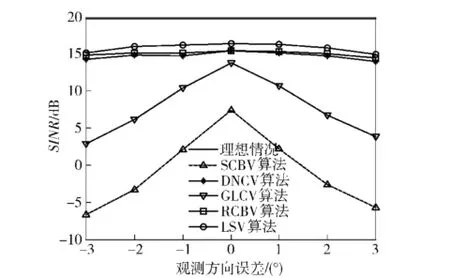
圖5 各算法性能隨觀測方向誤差變化曲線Fig.5 Output SINR versus observation direction errors

3.3 對快拍數不足穩健性對比

分別考察存在隨機導向矢量誤差和觀測方向誤差時,各算法的性能隨快拍數變化曲線,其中期望信號輸入信噪比均為10 dB.圖6顯示存在實驗1所述隨機導向矢量誤差且σ=0.1時,各算法的性能隨快拍數變化曲線。圖7顯示存在1°觀測方向誤差時,各算法性能隨快拍數變化曲線。從圖6和圖7可以看出,存在上述導向矢量失配時,相同快拍數下DNCV和SCBV算法性能相當,而本文算法輸出信干噪比較二者約高1 dB.值得注意的是,GLCV算法性能隨快拍數的增加有下降的趨勢,這是因為隨快拍數的增加,GLCV算法生成的對角加載量減少,而逐漸喪失了抵抗導向矢量失配的穩健性。

3.4 對矢量傳感器姿態誤差穩健性對比

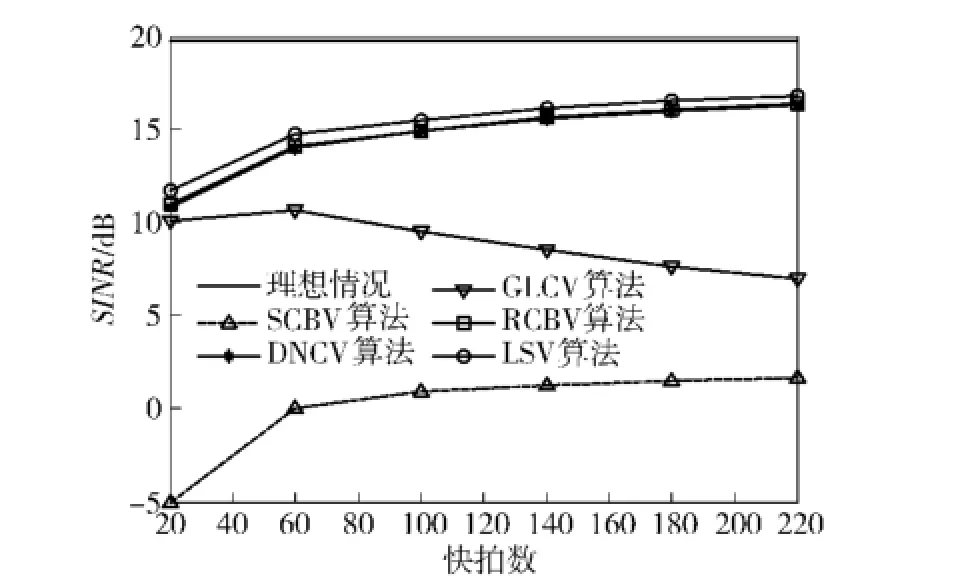
圖6 存在隨機導向矢量誤差時各算法性能隨快拍數變化曲線Fig.6 Output SINR versus the number of snapshots in the presence of array calibration error

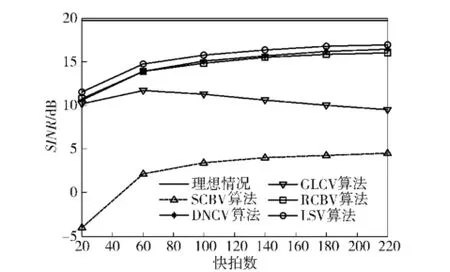
圖7 存在觀測方向誤差時各算法性能隨快拍數變化曲線Fig.7 Output SINR versus the number of snapshots in the presence of observation direction error

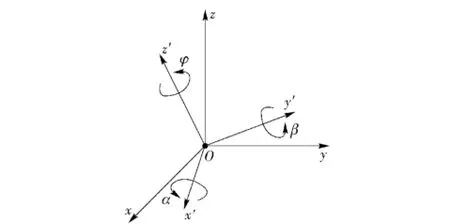
圖8 矢量傳感器姿態誤差模型Fig.8 Attitude error model of vector-sensor array

廣義歐拉角是描述剛體旋轉常用的方法[9]。單聲矢量傳感器原始姿態如圖8中Oxyz所示,其他任意姿態都可由下述三次轉動獲得:1)先繞z軸轉φ角;2)然后繞體軸y(在新位置)轉β角;3)最后繞體軸x(在新位置)轉α角。新姿態下的矢量陣振速通道導向矢量可由文獻[9]中廣義歐拉角表示。假設導向矢量誤差由姿態誤差引起,其中α、β、φ均服從均值為0,標準差為δ的高斯分布,期望信號信噪比為10 dB,快拍數為100.圖9顯示各算法的輸出信干噪比隨姿態誤差的標準差變化曲線。從圖中可以看出,本文算法和DNCV算法性能受姿態誤差影響較小,而在相同的姿態誤差下,本文算法輸出信干噪比更高。

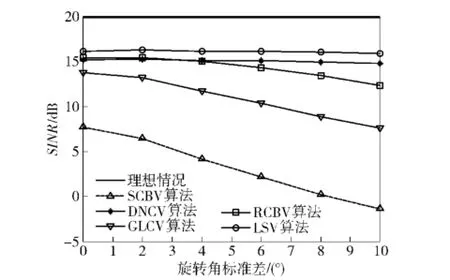
圖9 各算法性能隨姿態誤差標準差變化曲線Fig.9 Output SINR versus standard deviation of attitude errors

4 結論

相比于標量陣,矢量陣自適應波束形成器更易受導向矢量誤差和快拍數不足的影響,針對上述問題,提出了一種基于LSV估計的穩健波束形成算法。首先分別對聲矢量陣聲壓通道和兩個振速通道設計廣義旁瓣對消器,利用常規波束形成器權值提取信號和干擾成分,利用自適應權值提取用于抵消的干擾成分,從而提高輸出信干噪比。通過求解數據協方差矩陣范數約束下的最小二乘估計問題,保證算法的穩健性。仿真分析表明,該算法在抗隨機導向矢量誤差、觀察方向誤差、快拍數不足和矢量傳感器姿態誤差方面均有良好的性能。

References)

[1] Song A,Abdi A,Badiey M,et al.Experimental demonstration of underwater acoustic communication by vector sensors[J].IEEE Journal of Oceanic Engineering,2011,36(3):454-461.

[2] Poulsen A J,Nadakuditi R R,Baggeroer A B.Robust adaptive vector sensor processing in the presence of mismatch and finite sample support[C]∥Sensor Array and Multichannel Signal Processing Workshop,SAM 2008.Darmstadt:IEEE,2008:473-477.

[3] 劉凱,梁國龍,張光普.初探陣列誤差對矢量陣波束形成系統的影響[J].系統仿真學報,2012,24(4):848-853.

LIU Kai,LIANG Guo-long,ZHANG Guang-pu.Exploratory analysis to influence of array errors on vector-sensor array beam-forming system[J].Journal of System Simulation,2012,24(4):848-853.(in Chinese)

[4] 宋海巖,樸勝春,秦進平.基于矢量最優化的穩健波束形成[J].兵工學報,2012,33(10):1222-1229.

SONG Hai-yan,PIAO Sheng-chun,QIN Jin-ping.Robust adaptive beamforming based on vector optimization[J].Actc Armamentarii,2012,33(10):1222-1229.(in Chinese)

[5] Du L,Li J,Stoica P.Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(1):449-458.

[6] Li J,Stoica P,Wang Z S.On robust capon beamforming and diagonal loading[J].IEEE Transactions on Signal Processing, 2003,51(7):1702-1715.

[7] Zhang Y W,Sun D J,Zhang D L.Robust adaptive acoustic vector sensor beamforming using automated diagonal loading[J].Applied Acoustic,2009,70(8):1029-1033.

[8] 劉凱.聲吶波束形成魯棒性及算法研究[D].哈爾濱:哈爾濱工程大學,2011.

LIU Kai.Research on robustness and algorithm of sonar beamforming[D].Harbin:Harbin Engineering University,2011.(in Chinese)

[9] 梁國龍,劉凱,溫韶娟,等.基于洛倫茲規劃的聲矢量陣寬容自適應波束形成[J].聲學技術,2011,30(1):98-101.

LIANG Guo-long,LIU Kai,WEN Shao-juan,et al.Robust adaptive beamforming of acoustic vector sensor array based on Lorenz cone programming[J].Technical Acoustic,2011,30(1):98-101.(in Chinese)

[10] Yu Z L,Hwa Er M.A robust minimum variance beamformer with new constraint on uncertainty of steering vector[J].Signal Processing,2006,86(9):2243-2254.

[11] Selèn Y,Abrahamsson R,Stoica P.Automatic robust adaptive beamforming via ridge regression[J].Signal Processing,2008, 88(1):33-49.

[12] Boyd S P,Lieven V.Convex optimization[M].Cambridge: Cambridge University Press,2004:561-623.

[13] Samuel DSomasundaram.Robust Capon beamforming with additional linear constraints[C]∥2011 IEEE Statistical Signal Processing Workshop.Nice:IEEE,2011:145-148.

[14] Shahbazpanahi S,Gershman A B,Luo Zhi-quan,et al.Robust adaptive beamforming for general-rank signal models[J].IEEE Transactions on Signal Processing,2003,51(9):2257-2269.

[15] Zeng X Y,Wang S G.Bark-wavelet analysis and Hilbert-Huang transform for underwater target recognition[J].Defence Technology,2013,9(2):115-120.

[16] Lu Z H,Zhang Z H,Gu J N.Numerial calculation of seafloor synthetic seismograms caused by low frequency point sound source [J].Defence Technology,2013,9(2):98-104.

[17] Jian L,Lin D,Stoica P.Fully automatic computation of diagonal loading levels for robust adaptive beamforming[J].IEEE Transactions on Aerospace and Electronic System,2010,46(1):449 -458.

Robust Adaptive Beamforming of Acoustic Vector-sensor Array Based on Least Squares Estimation

WANG Yan,WU Wen-feng,LIANG Guo-long
(Science and Technology on Underwater Acoustic Laboratory,Harbin Engineering University,Harbin 150001,Heilongjiang,China)

The performance of Capon beamformer of acoustic vector-sensor array degrades sharply in the presence of array steering vector mismatch.A robust beamforming algorithm based on least squares estimation is proposed to solve this problem.Several generalized sidelobe cancellers are designed for acoustic pressure channel and vibration velocity channel in consideration of the different error sources of their steering vectors.The Capon beamformer of acoustic vector-sensor array is converted to a robust leastsquares estimation problem based on the principle of worst-case performance optimization.The second-order cone programing is adopted to obtain the optimal solution.The simulation results show the efficiency of the proposed algorithm in the cases of steering vector mismatch,snapshot deficiency and sensor attitude error.

information processing;robust adaptive beamforming;acoustic vector-sensor array;generalized sidelobe canceller;least squares estimation

TB566

:A

1000-1093(2014)03-0379-06

10.3969/j.issn.1000-1093.2014.03.013

2013-05-07

國家自然科學基金項目(51279043、61201411、51209059);海軍裝備預先研究項目(1011204030104);水聲技術國家重點實驗室基金項目(9140C200203110C2003);黑龍江省普通高校青年學術骨干支持計劃項目(1253G019)

王燕(1973—),女,教授,博士生導師。E-mail:wangyan@hrbeu.edu.cn;吳文峰(1987—),男,博士研究生。E-mail:wwf@hrbeu.edu.cn