起伏地形條件下FPS不同解釋方法對比

肖 波，劉海飛，戴前偉

(1.廣東省電力設計研究院，廣州 510600；2.中南大學 地球科學與信息物理學院，長沙 410083)

0 前言

固定點源激電測深法(FPS)又稱固定點源雙邊三極測深法(圖1)。由前蘇聯柯馬羅夫B.A[1]于60年代提出。工作中供電正極A固定不動，供電負極B置于無窮遠處，測量電極MN在A極兩邊移動。該方法測量極距可根據實際情況靈活變化，導體極化場位置隨著供電點位置變化而變化，且在工作中能采用多臺接收機同時測量，在具有較高工作效率的同時可更換確定極化體的空間位置。但該裝置在數據處理過程中，常規的相對強度-圓弧交匯定量解釋法對于簡單地電條件下的模型解釋通常能取得較好效果，但在起伏地電條件下，其解釋效果通常會受到較為明顯的地形影響，從而未能精確確定極化體的中心深度及上界面位置，為勘探解釋工作帶來困難。

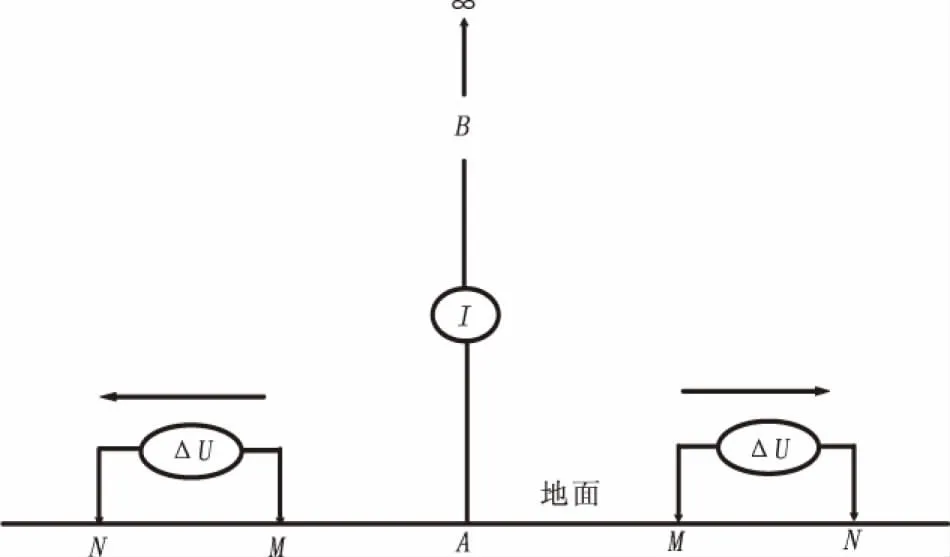
圖1 固定點源測深法裝置簡圖Fig．1 The fixed point source IP sounding equipment

對此從有限元正演模擬和最小二乘反演方法的角度入手，對起伏地形條件下的地電模型進行實例計算，并將最小二乘反演結果與圓弧交匯—相對強度計算結果相對比。由對比結果表明：最小二乘反演方法能較好地適應起伏地形條件進行反演計算，其反演效果優于相對強度-圓弧交匯定量解釋法，能更有效地體現出實際異常體的真實信息。

1 正演模擬

正演模擬采用有限單元法進行計算。將二維地電斷面區域離散成許多相互連接的網格單元，對各個網格單元節點電位進行求解得到地電斷面的電位分布，通過將電位分布轉化為視電阻率從而得到斷面各個節點的電阻率值，根據“等效電阻率”公式求取出視極化率值。

在二維地電條件下，點源場中各網格節點的電位計算可歸結為對若干個給定波數λ求解電位的傅氏變換v(x,λ,z)所滿足的二維偏微分方程的邊值問題：

(1)

(2)

采用有限單元法對變分問題求解，得出變換電位V(x,λ,z)，作傅里葉逆變換：

將電位分布值轉化為視電阻率值，通過“等效電阻率”求取，從而得到視極化率值。

2 解釋方法

2.1 常規定量解釋方法

在電法勘探中，通過以兩個以上的供電點到ρs/ηs曲線極值點P的距離為半徑，分別在二維地電斷面上做圓弧，圓弧的交點位置近似為異常體的空間中心位置，該作圖方法稱為圓弧交匯法[3-4]，如圖2所示。

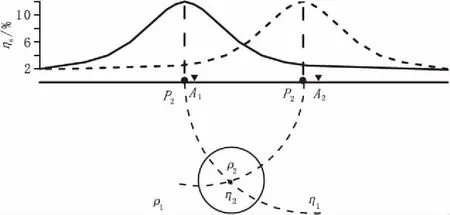
圖2 圓弧交匯法示意圖Fig．2 Diagram of arc intersection method

相對強度法是以圓弧交匯法為基礎，將二維地電斷面網格化并以點源為圓心，以點源到各網格節點的距離為半徑作圓弧，取圓弧與水平地表交點位置對應的視電阻率/視極化率在地表的投影值為該網格節點的值，位于點源坐標左、右邊的網格節點值分別由視電阻率/視極化率左、右支實測值確定。對于多個點源，先對各節點上 求和進而計算出他們的平均值 找出斷面上最大的平均值 ，用各網格節點的平均值 去除以 ，從而得到了相對強度值 ；對于低阻體則相反，提取斷面上最小平均值 并用該值除以網格各節點的平均值 ，從而達到突出斷面異常體的中心位置的目的。相對強度法的作圖如圖3所示。

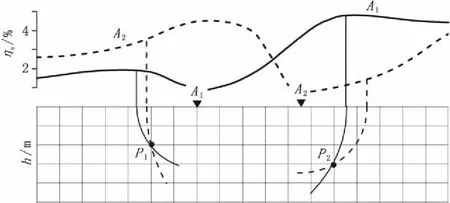
圖3 相對強度法的成圖示意圖Fig．3 Diagram of relative intensity method

2.2 最小二乘反演

反演采用基于圓滑約束的最小二乘反演方法，利用實測數據和正演模型構造一目標函數，并使其達到極小。圓滑約束最小二乘是基于以下方程[5～6]：

(JTJ+λCTC)Δm=JTΔd+λCTC(mb-m)

(3)

式中 Δm=m-m0：模型參數修改矢量(m為N維模型參數矢量，m0為初始模型參數矢量)；mb為基本模型參數矢量；Δd=d-d0：數據殘差矢量(d為M維實測視電阻率向量，d0為初始模型的觀測值)；J為偏導數矩陣;λ為拉格朗日乘數；C為光滑度矩陣。

對方程組(3)求解從而得到模型參數修正矢量Δm，并將其代入：

m(k)=m(k-1)+Δm

(4)

從而得到預測模型參數矢量m(k)。如此重復，直至實測數據與模型數據之間的平均均方誤差滿足要求為止，電阻率反演過程結束[7-9]。平均均方誤差的計算公式為：

(5)

3 模型計算

采用有限單元法進行正演計算，分別用圓弧交匯—相對強度法、最小二乘反演進行計算。將多個模型實例進行模型計算，并將兩種不同計算方法的進行對比分析。

綜合考慮數據量、反演效果及工作量之間的關系，擬布設7個測深供電點：A1=40 m、A2=60 m、A3=80 m、A4=100 m、A5=120 m、A6=140 m、A7=160 m。為取得有效勘探精度與深度，模擬測線為-50 m～250 m，實取測線0 m～200 m數據進行剖面成圖。計算結果剖面圖中的藍色方框為模型投影圖(圖4)。

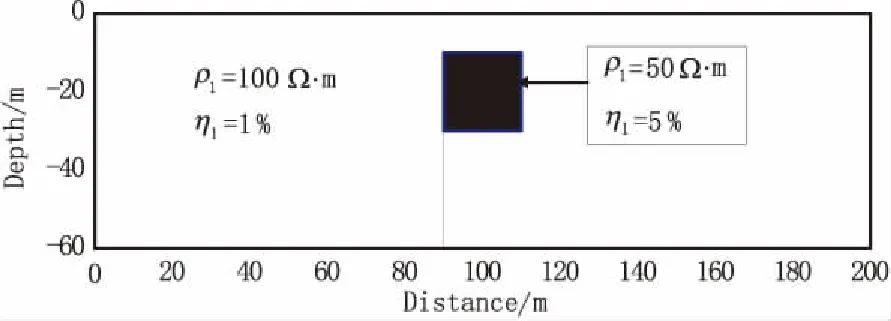
圖4 水平地形下正方柱體模型示意圖Fig．4 Schematic diagram of affirmative column model under horizontal topography

3.1 水平地形

模型為一個20 m×20 m低阻、高極化正方柱體(見圖4)；中心位置(100 m,-20 m)，電阻率ρ1=50 Ω·m，極化率η1=5.0%；背景電阻率ρ0=100 Ω·m，極化率：η0=1.0%。正演模擬計算得到的各點源視電阻率、視極化率曲線如圖5、圖6所示。視電阻率、視極化率相對強度圖如圖7、圖8所示。視電阻率、視極化率最小二乘反演結果如圖9、圖10所示。

圖5 水平地形下正方柱體模型正演模擬各點源測深視電阻率曲線圖Fig．5 The apparent resistivity curve of affirmative column model under horizontal topography

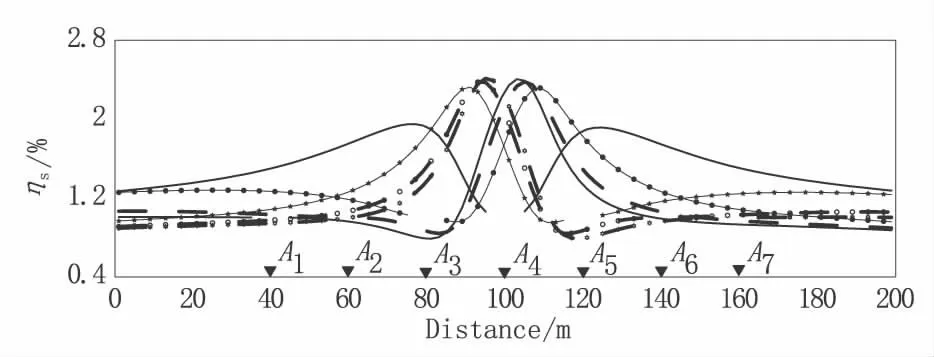
圖6 水平地形下正方柱體模型正演模擬各點源測深視極化率曲線圖Fig．6 The polarizability curve of affirmative column model under horizontal topography

圖7 正方柱體模型正演視電阻率相對強度圖Fig．7 The arc intersection - relative intensity result of apparent resistivity about affirmative column model under horizontal topography

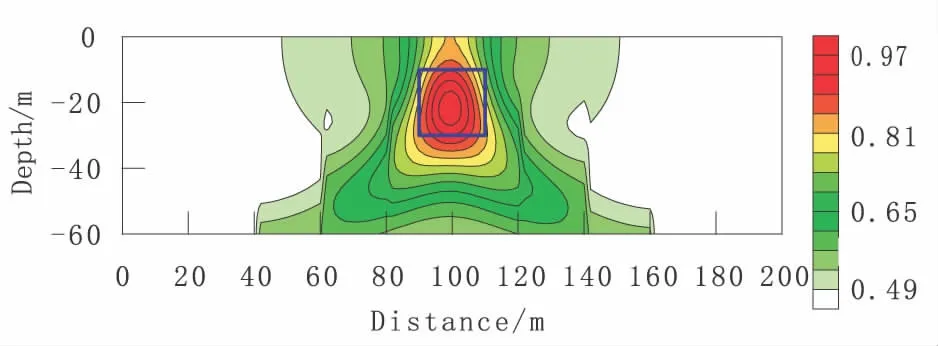
圖8 水平地形下正方柱體模型正演視極化率相對強度圖Fig．8 The arc intersection - relative intensity result of polarizability about affirmative column model under horizontal topography

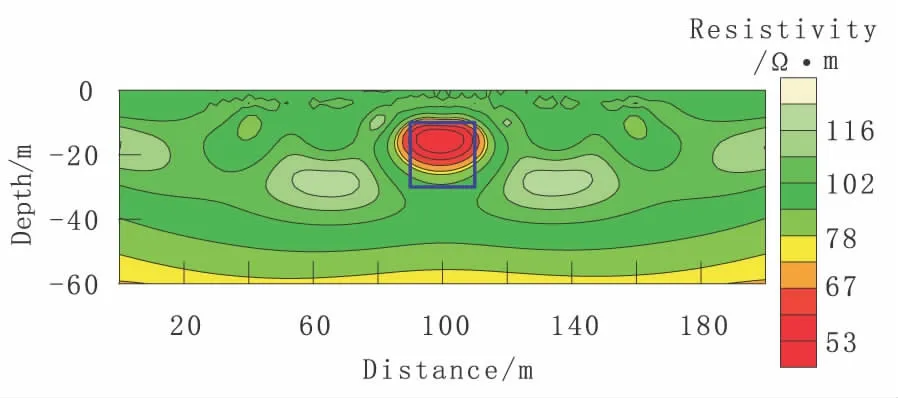
圖9 水平地形下正方柱體模型視電阻率最小二乘反演結果Fig．9 The least square inversion result of apparent resistivity about affirmative column model under horizontal topography

圖10 水平地形下正方柱體模型視極化率最小二乘反演結果Fig．10 The least square inversion result of pola-rizability about affirmative column model under horizontal topography

由圖7、圖8可知：圓弧交匯—相對強度法計算結果能很好地反映出正方柱體的中心埋深。該異常體中心位置與模型中心位置吻合關系好，但該異常相對強度等值線圖不能體現模型的基本形態，且異常范圍較實際模型大。

對比發現：圖9、圖10表明最小二乘反演能較好地反映模型的基本形態和基本位置，其異常范圍與模型大小基本一致，但最小二乘反演結果未能精確反映出模型極化體中心，反演結果中極化體中心位于實體模型中上部位置。

3.2 山谷地形

模型為一個低阻、高極化長方體模型(圖11)。模型中心位置，電阻率為，極化率為η1=5.0%，模型中心頂面與地表相距；背景電阻率，背景極化率η0=1.0%。正演模擬計算得到的各點源視電阻率、視極化率曲線如圖12、圖13所示。修正后的圓弧交匯—相對強度法[7]計算結果如圖14、圖15所示。視電阻率、視極化率最小二乘反演結果如圖16、圖17所示。

圖11 山谷地形下長方體模型示意圖Fig．11 Schematic diagram of cuboid model under valley topography

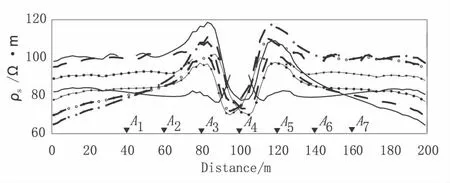
圖12 山谷地形下長方體模型正演模擬各點源測深視電阻率曲線圖Fig．12 The apparent resistivity curve of cuboid model under valley topography

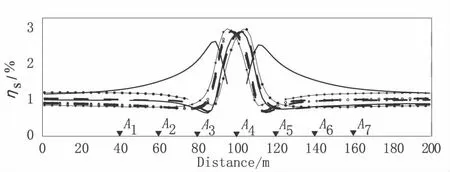
圖13 山谷地形下長方體模型正演模擬各點源測深視極化率曲線圖Fig．13 The polarizability curve of cuboid model under valley topography

圖14 山谷地形下長方體模型正演視電阻率相對強度圖Fig．14 The arc intersection - relative intensity result of apparent resistivity about cuboid model under valley topography

由圖14、圖15可知：圓弧交匯—相對強度法計算結果能確定模型的基本位置，但異常體的相對強度中心與模型實際位置不相吻合，異常體中心位置位于實際模型底界面處，同時異常體的基本形態、大小與模型實際存在較大差距。其原因為由于山谷地形影響，模型的異常范圍變窄導致異常體極大值點與其對應的電源點距離縮短；對于山脊而言剛好相反，模型的異常體范圍變大導致異常體極大值點與其對應的電源點距離變大。盡管再做圓弧交匯-相對強度進行成圖計算時已進行地形校正處理，但地形影響在一定程度上仍然存在，當極化體埋深逐漸增大時，該影響隨之減弱。

對比發現：圖16、圖17表明最小二乘反演能更好地反映出模型的基本形態及空間位置，異常體的基本輪廓及中心埋深位置與實際模型吻合關系一致。

3.3 山脊地形

模型為一個 低阻、高極化長方體模型(圖18)，模型中心位置，電阻率 ，極化率η1=5.0%，模型中心頂面與地表相距5 m；背景電阻率 ，背景極化率η0=1.0%。正演模擬計算得到的各點源視電阻率、視極化率曲線如圖19、圖20所示。圓弧交匯-相對強度法計算結果如圖21、圖22所示。視電阻率、視極化率最小二乘反演結果如圖23、圖24所示。

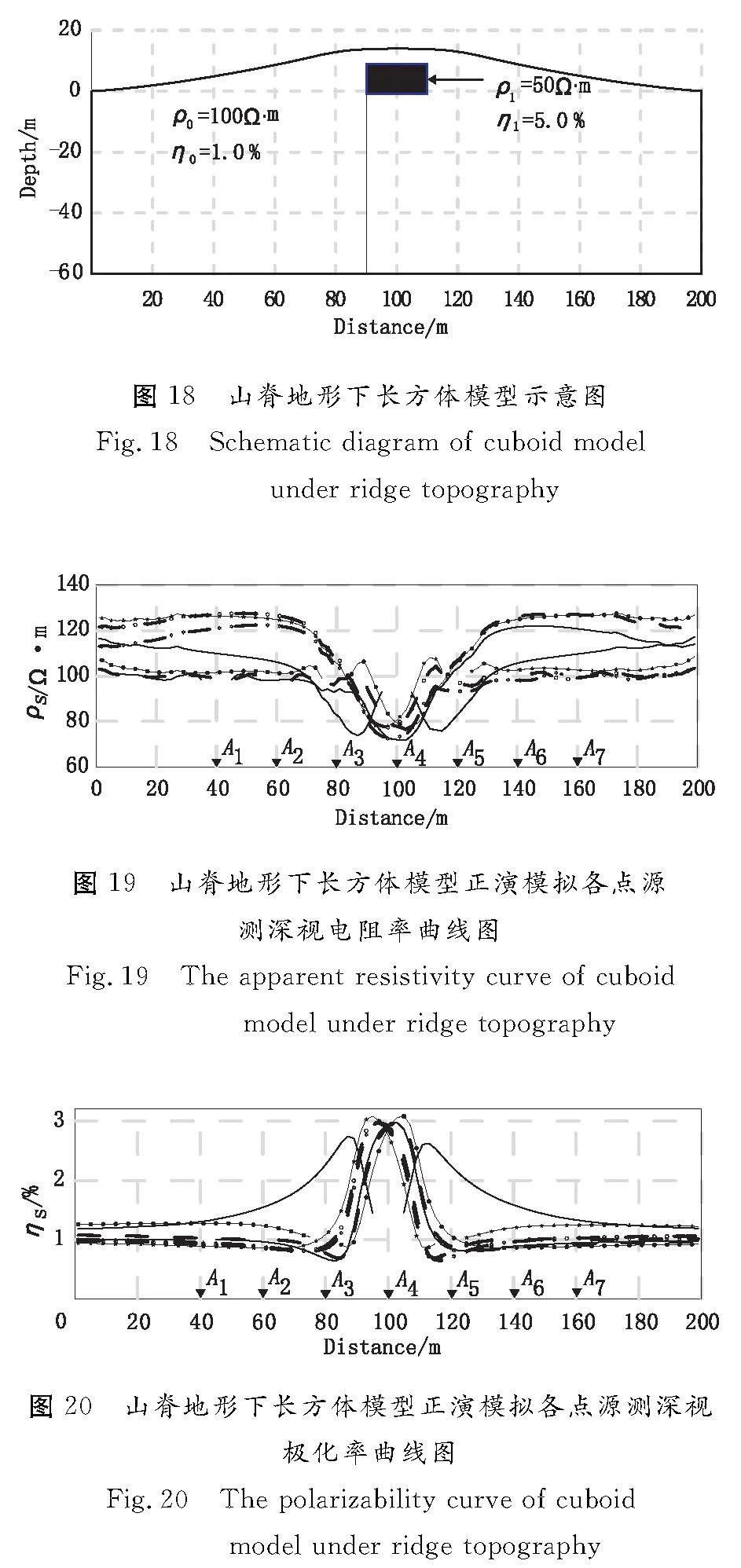
由圖21、圖22可知：圓弧交匯-相對強度法計算結果能確定模型的基本位置，但異常體的相對強度中心與模型實際位置不相吻合，異常體中心位置位于實際模型的底界面位置。此外不能根據異常體準確推斷出模型的大小及產狀。

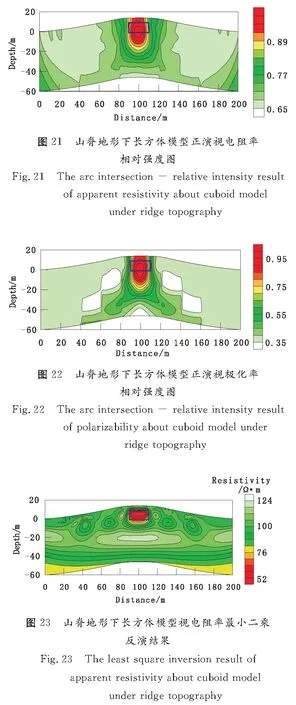
圖24 山脊地形下長方體模型視極化率最小二乘反演結果Fig．24 The least square inversion result of polari-zability about cuboid model under ridge topography

相比較而言：圖23、圖24表明最小二乘反演能較好地反映模型的基本形態及空間位置。反演結果中異常體中心位置及輪廓與實際模型中心位置及邊界吻合關系好，反演結果表明，最小二乘法反演能較好地適應起伏地形進行計算。

4 結論

(1)在水平地形條件下，圓弧交匯-相對強度法與最小二乘反演都能較好地反映出模型異常體的空間位置，圓弧交匯-相對強度法在確定異常體中心位置甚至優于最小二乘反演計算結果。

(2)在起伏地形條件下，圓弧交匯-相對強度法與最小二乘反演都能較準確地反映出異常體中心位置，兩種解釋方法直觀且其解釋效果與實際較為符合。

(3)采用圓弧交匯-相對強度法進行作圖解釋，其地形影響在一定程度上仍然存在。此外難以根據異常體輪廓準確推斷出模型的大小及產狀。

(4)最小二乘反演結果能較好地反映出模型的基本形態及空間位置。反演結果剖面圖中異常體中心位置及其輪廓模型中心位置吻合及模型邊界吻合關系好，表明最小二乘法反演能很好地適應起伏地形進行反演計算，其反演結果優于圓弧交匯-相對強度法。

參考文獻：

[1] KOMAPOBB А.Теоретическиеосновыинтерпретацийн-аблюденийВметодевызваннойполяризаций[M],Л.Недра,1966.

[2] 戴前偉,肖波,馮德山，等. 基于二維高密度電阻率勘探數據的三維反演及應用[J].中南大學學報：自然科學版,2012, 43(1): 0293 -0310.

[3] 劉國興.電法勘探原理與方法[M].北京.地質出版社.2005.

[4] 李金銘.地電場與電法勘探[M].北京,地質出版社,2005.

[5] 李金銘,魏文博,陳本池,等.固定點源測深法定量解釋研究[J].物探與化探,1997,21(3):187-196.

[6] 強建科,羅延鐘,熊彬.固定點源測深激電異常研究[J].地球物理學進展,2005,20(4):1176-1183.

[7] 熊彬,阮百堯,黃俊革. 直流電阻率測深中二維反演程序對三維數據的近似解釋[J].地球科學-中國地質大學學報, 2003,28(1):0102-0106.

[8] 劉海飛.高密度數據處理方法研究[D].長沙:中南大學信息物理工程學院,2003.

[9] 張大海,王興泰.二維視電阻率斷面的快速最小二乘反演[J].物探化探計算技術, 1999, 21(1)：2-8.