巧用開普勒第三定律解決天體運動問題

吳正飛

(如東高級中學 江蘇 南通 226400)

自古以來，人們一直對天體的運動進行著長期的探索和研究，從亞里士多德和托勒密主張的地心說到哥白尼提出日心說再到第谷對行星的運動進行了長期的觀測和記錄，最終德國杰出的天文學家開普勒在第谷精確數據的基礎上進行了創造性的研究和思考并建立了行星運動的三大定律．其中包括開普勒第一定律(軌道定律)、開普勒第二定律(面積定律)、開普勒第三定律(周期定律)．

下面重點研究開普勒第三定律在天體運動問題中的巧妙應用．

開普勒第三定律：所有行星的軌道的半長軸的三次方跟公轉周期的二次方的比值都相等．即

式中a為半長軸，T為公轉周期.

1 開普勒第三定律解決同“中”行(衛)星問題

開普勒第三定律雖然是根據行星繞太陽的運動總結出來的，但對于衛星繞行星的運動也同樣適用．在天體運動中經常遇到繞同一個中心天體運動的行星或衛星問題，此時可利用開普勒第三定律建立行星或衛星之間的半徑和周期之間的聯系．

【例1】哈雷彗星最近出現的時間是1986年.天文學家哈雷預言，這顆彗星將每隔一定時間就會出現，請預算下一次飛近地球是哪一年？提供數據：

(1)地球公轉接近圓，彗星的運動軌道則是一個非常扁的橢圓，如圖1所示；

(2)彗星軌道的半長軸R1約等于地球軌道半長軸R2的18倍．

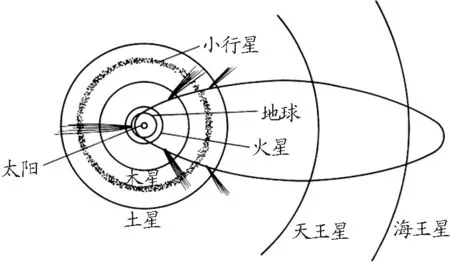
圖1

解析：設彗星繞太陽運動的周期為T1，地球的公轉周期為T2，根據開普勒第三定律，有

解得

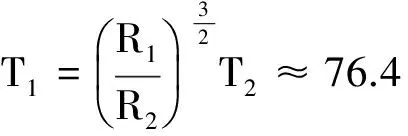
則哈雷彗星下次出現的時間是

1986年 + 76年 = 2062年

解題點撥:在解決同“中”行(衛)星問題時，必須抓住相同的中心天體這個開普勒第三定律適用的關鍵條件，然后由軌道半徑就可以確定周期，或由周期就可以確定半徑，從而找到問題的突破口，解決問題．

2 開普勒第三定律解決同步衛星問題

同步衛星問題是高中階段學習中的常見問題，是人造衛星中的重點也是難點．一般需要掌握同步衛星的位置、周期、高度、線(角)速度等，根據同步衛星和其他衛星均以地球為中心，符合開普勒第三定律的適用條件，因此利用開普勒第三定律和其他衛星的周期或半徑就可求得同步衛星對應的周期和高度等．

【例2】月球環繞地球運動的軌道半徑約為地球半徑的60倍，其運行周期約為27天，現應用開普勒定律計算：在赤道平面內，離地多高時，人造地球衛星可隨地球一起轉動，就像其停在天空一樣(同步衛星)．(已知R地= 6.4×103km)

解析：設同步衛星運動的半徑為R1，周期為T1(此周期與地球自轉周期相同)，月球的軌道的半徑為R2，周期為T2，根據開普勒第三定律有

解得

則同步衛星離地面的高度為

h=R1-R地=5.67R地=3.63×106m

解題點撥:月球、同步衛星都是地球的衛星，它們的周期已知，應用開普勒第三定律可以確定它們軌道半徑之間的關系，從而使問題簡化．

3 開普勒第三定律解決變軌問題

衛星在軌期間自主改變運行軌道的過程稱為變軌．人造衛星、宇宙飛船(包括空間站)在軌道運行的過程中，常常需要變軌．變軌過程中衛星的軌道為橢圓，地球處于焦點上．在變軌問題中通常需要計算運行時間，因其軌道不是圓，所以不能利用圓周運動的知識求解．

若利用開普勒第三定律求解，問題就會變得非常簡單，但要注意公式中的a分別是變軌前圓周運動的半徑和變軌中的橢圓軌道的半長軸．

【例3】飛船沿半徑為R的圓周繞地球運動，其周期為T，如圖2所示.如果飛船要返回地面，可在軌道上的某點A將速度降低到適當的數值，從而使飛船沿著地心為焦點的橢圓軌道運行，橢圓與地球表面在B點相切，求飛船由A點到B點所需的時間．(已知地球半徑為R0)

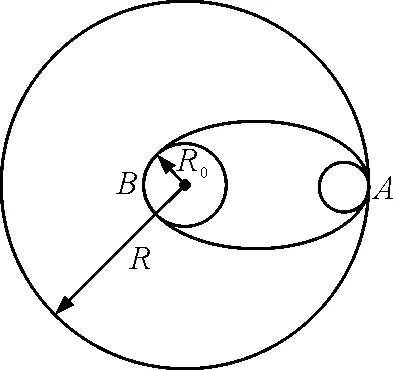
圖2

解析：無論飛船是沿圓軌道運行還是沿橢圓軌道運行，飛船都是繞地球運動，所以運行時間與半徑之間的關系滿足開普勒第三定律，由

解得

則飛船由A點到B點所需的時間為

解題點撥:變軌在衛星運行中很常見，變軌過程中由于衛星始終繞同一天體運動，所以開普勒第三定律仍然適用，只要能明確對應的周期和半徑，問題就會迎刃而解．

4 開普勒第三定律解決衛星“追及和相遇”問題

地面上的物體常常出現追及和相遇問題，關鍵是找出它們的位移、速度和時間等關系，運動路線應該在同直線上．天體運動中也有追及和相遇問題，它與地面上的追及相遇問題在思維有上相似之處，即也是找出一些物理量的關系，但它也有不同之處，有其自身特點．一般根據萬有引力提供向心力和圓周運動的知識求解，但過程較繁．若利用開普勒第三定律來建立兩者之間的半徑和周期的關系，則會令問題簡化．但要注意當天體速度增加或減少時，對應的圓周軌道會發生相應的變化，所以天體不可能在同一軌道上追及或相遇，但可到達與中心天體同一連線上，此時通常我們也可認為衛星即相遇．

【例4】某行星和地球繞太陽公轉的軌道均可視為圓．每過N年，行星會運行到日地連線的延長線上，如圖3所示．求該行星與地球的公轉半徑的比值．

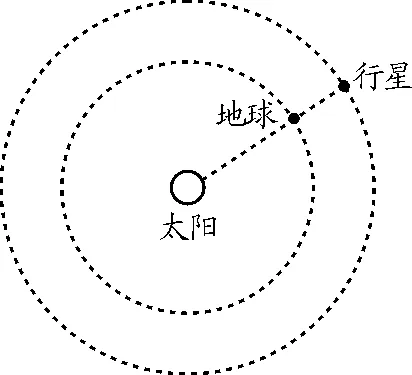
圖3

解析:從行星運動到日地連線的延長線上到下一次再到日地連線延長線上，地球比該行星轉過的角度大2π ，設行星的周期為T,由此可知

即

解得

又地球與該行星都繞太陽轉，則根據開普勒第三定律得

所以

解題點撥：兩衛星繞同一中心天體運動，半徑與周期的關系可由開普勒第三定律確定．不同軌道上的衛星不能直接追及和相遇，但可到達與中心天體同一連線上，通過圓心角找到周期關系，進而解決半徑問題．

本文重點介紹了開普勒第三定律在同“中”行星、同步衛星、以及衛星變軌、追及這4類問題中的應用．開普勒第三定律是解決天體運動問題的重要途徑．在應用過程中，我們只要抓住“一個中心”(同一中心天體)，找到“兩者關系”(周期和半徑關系)，問題定會迎刃而解．