關于既有接觸網大修中心錨結位置設置的探討

黃 河

0 引言

在既有線接觸網大修時，往往會遇到由于支柱跨距的調整而使整個錨段縮短或增長的情況。由此，該錨段內中心錨結位置若仍在既有位置，則可能由于錨段長度改變和線路情況變化引起線索張力增量變化導致線索張力不均和定位器、腕臂偏移量大等問題。本文對既有線接觸網改造錨段長度變化后，重新設置中心錨結位置作一些分析和探討。

1 中心錨結的安設

在兩端裝設補償器的接觸網錨段中，必須加設中心錨結。每個錨段中心錨結安設位置應根據線路情況和線索的張力增量計算確定。一般布置原則是使中心錨結固定點兩側線索的張力盡量相等，并盡可能靠近錨段中部。

當錨段全部在直線區段或整個錨段布置在曲線半徑相同的曲線區段時，該錨段中心錨結應安設在錨段的中間位置。

當錨段布置在既有直線又有曲線且曲線半徑不等的區段時，該錨段的中心錨結應設在曲線多、曲線半徑小的一側。在特殊情況下，錨段長度較短時（一般定為錨段長度800 m以下），可不設中心錨結，視為半個錨段，可將錨段一端硬錨，另一端線索安裝補償器，此時的硬錨就相當于中心錨結。

2 影響中錨位置的因素

在既有網大修時選擇中心錨結位置時應充分考慮以下幾方面：

（1）接觸懸掛在線路坡道處，由于懸掛本身的重量沿下坡方向產生作用于懸掛的分力。

（2）曲線上因旋轉腕臂偏轉，出現對線索向某一方向的分力作用。

（3）一側下錨轉角過大時，會限制腕臂隨溫度的偏移。

（4）風力和受電弓對接觸線的滑動摩擦力方向等。

（5）錨段長度變化和錨段位置變化后，線索由于線路情況發生變化而導致張力變化。

以上原因都可能造成中心錨結兩端張力不平衡，有時可能會重疊出現，誘發接觸懸掛向某一方向產生竄動。

3 中心錨結的重新安設

當錨段長度變化時，若中心錨結位置仍在原位，勢必因中心錨結兩端張力差過大而造成吊弦、腕臂偏移量過大。這里需要說明一點，接觸網張力差是始終存在的，一般情況下（中錨位置適合），張力差值最多為最大張力的10%。

3.1 定位器形成的張力增量ΔTjW

定位器在溫度變化時也因接觸線產生伸長（或縮短）而發生偏轉。在直線區段上，由于定位器對接觸線張力變化影響很小（一般對1500 m長的錨段，其定位器產生的張力增量只有幾十 N），可以忽略。因此，對于定位器產生的張力增量，只考慮曲線上的情況。

為了確定接觸線因定位器的移動而引起的張力變化，需研究它們的平衡條件。

因為定位器的作用，在溫度變化時，接觸線產生張力增量ΔTjw，其受力情況如圖1和圖2所示[1]。

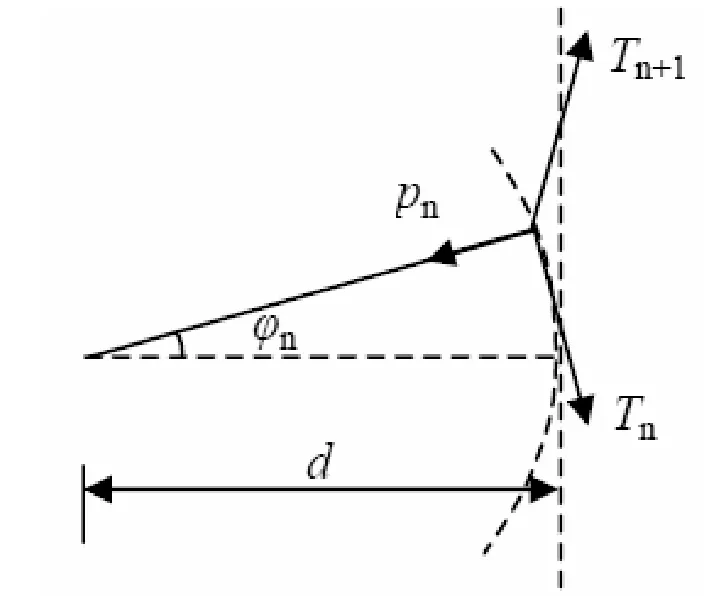
圖1 定位器偏移示意圖

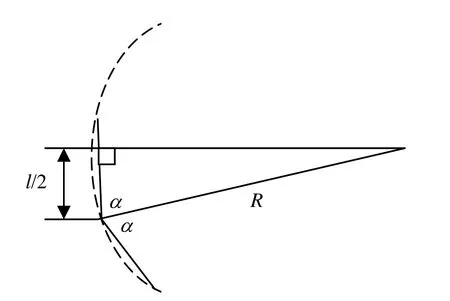
圖2 曲線區段懸掛平面圖

由結點各力對垂直軸和水平軸投影可得：

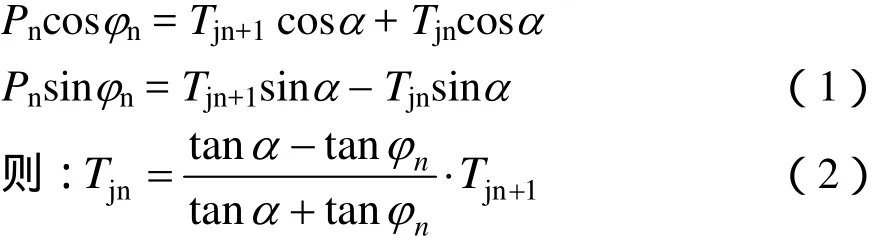
由圖1和圖2可知：

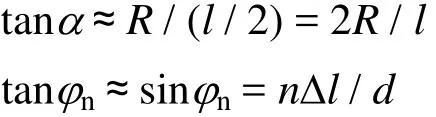
由中心錨結至補償器間因定位器作用而形成的張力增量為Tj1－Tjm，即：

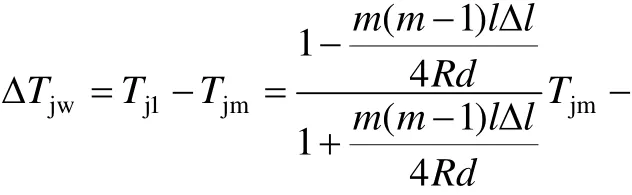
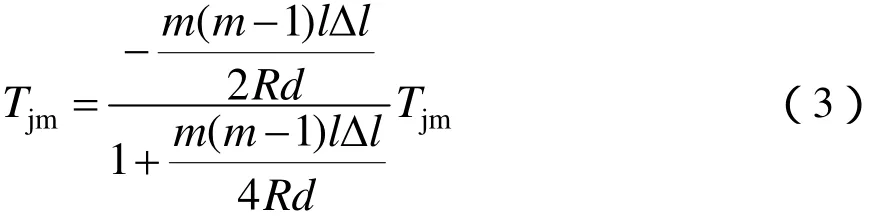
同前，將Δl = l(αΔl - ε)和 ml = L 代入上式，可得：

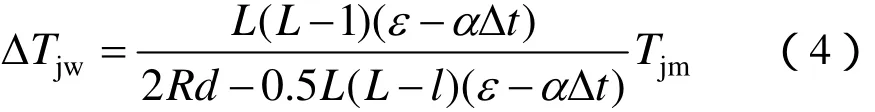
式中，Tjm為接觸線在補償處的張力，又稱為起始張力。其定位器形成張力增量ΔTjw與起始張力Tjm成比例。造成張力變化的原因，實際上是由吊弦和定位器共同作用的。因此，起始張力中必須考慮吊弦的影響。而ΔTjd是一個拋物線，其平均張力增量為(2/3)(ΔTjd)，所以計算定位器造成接觸線的張力差時，其起始張力應取：

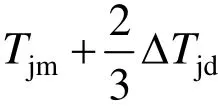
因而，由定位器的偏移對接觸線所引起的張力增量為

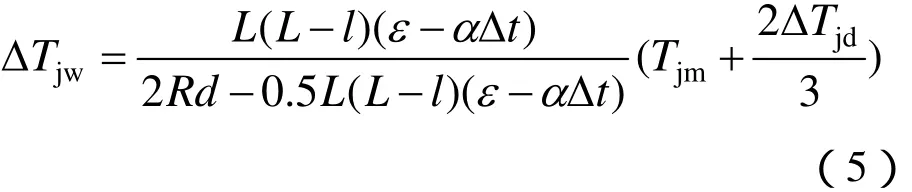
式（5）的應用條件為在曲線區段，且只考慮溫度伸長和定位器偏移所引起的張力變化。在全補償鏈形懸掛中，接觸線弛度的變化更小，因溫度變化而耗損于弛度變化方向的縱向位移也更小。故在計算中ε 可忽略不計，即令ε = 0。

3.2 吊弦造成的張力增量ΔTjd

現在先考慮在直線區段上，接觸線由于溫度變化而伸長，因吊弦偏移而造成接觸線內的張力變化。為分析方便，先取出錨段中第n個支柱點來分析張力增量的形成（圖3）。

在平均溫度時，吊弦處在垂直位置。當溫度變化后，由于接觸線的伸長（或縮短），吊弦最低點的位置由A變到B。因為是半補償，可以認為鏈形懸掛承力索不變，此時，接觸線的受力情況要發生變化。因吊弦的傾斜產生了水平分量，即為張力增量，其值為

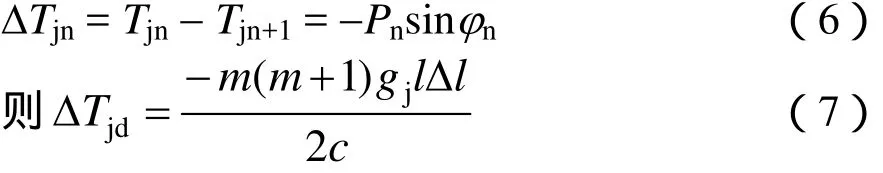
式中，m為半個錨段的跨距數；Δl為一個跨距內接觸線的伸長，其值為

令ml = L，代入式（7）得：

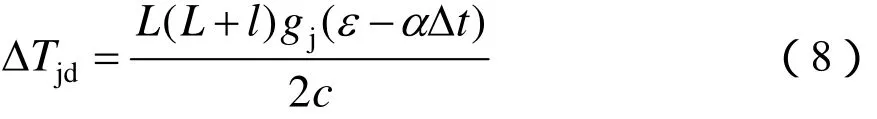
式中，ΔTjd為只考慮溫度變化時，吊弦所引起的張力增量，kN；gj為接觸線單位長度重量，kN/m；L為由中心錨結至補償器間的距離，m；c為吊弦長度，取平均值，為最短吊弦，其值為cmin= h - F0。

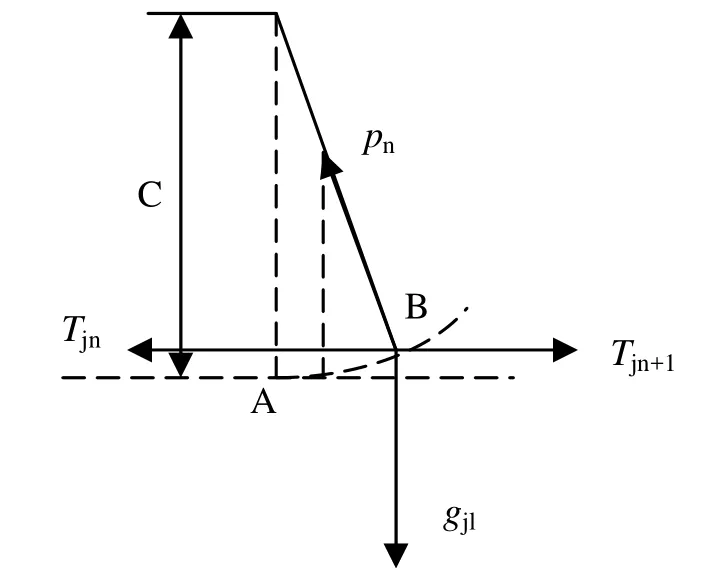
圖3 吊弦的偏移示意圖

式（8）的應用條件是在直線區段上；只考慮吊弦（Dx）所造成的張力變化和只考慮溫度引起的伸長。

在全補償鏈形懸掛中，接觸線弛度的變化更小，因溫度變化而耗損于弛度變化方向的縱向位移也更小。故在計算中ε 就忽略不計了，即令ε = 0。

3.3 中心錨結位置確定

在錨段長度和位置變化后，張力增量同樣不應大于最大張力的10%，按照該條件，對變化后的錨段長度和線路情況按照式（5）、式（8）反求 L，即可求得中心錨結至補償器間跨距數m。

4 算例

設懸掛形式為THJ-95+CTHA-120全補償簡單鏈形懸掛；承力索設計張力14.7 kN；接觸線設計張力14.7 kN；承力索單位重量5.85 kN /m；接觸懸掛單位重量16.93 kN /m，錨段長度1450 m，大部分位于曲線半徑600 m位置，跨距45 m。

由式（5），α = 17.6×10-6K-1，Δt = 20℃，得：L = 493 m，則，m = 11跨。

由式（8），得：L = 402 m，則，m = 9跨。

由以上計算可得出，該錨段中心錨結位置應靠曲線方向距離張力補償裝置10跨。

5 結語

通過本文的討論，對接觸網錨段長度和線路情況變化后中心錨結位置的設置做了簡單探討，得出了相應計算式，從而減小了新設錨段內吊弦、腕臂等設備偏移量，并能夠直接指導現場施工。希望本文能給遇到類似問題的工程技術人員提供幫助。

[1]于萬聚.高速電氣化鐵路接觸網[M].成都：西南交通大學出版社，2003.