小樣本下改進的PWM方法及其在導彈精度評定中的應用

呂鵬，袁永生，相榮霞，戴啟璠

(1.河海大學理學院，南京 210098;2.江蘇省灌溉總渠管理處，江蘇淮安 223200)

小樣本下改進的PWM方法及其在導彈精度評定中的應用

呂鵬1，袁永生1，相榮霞1，戴啟璠2

(1.河海大學理學院，南京 210098;2.江蘇省灌溉總渠管理處，江蘇淮安 223200)

針對運用經典統計方法對武器系統試驗的小樣本數據進行分析時存在的不足，基于小樣本特征，研究了改進的PWM區間估計方法。通過數據模擬，分別在正態分布、泊松分布以及指數分布下比較了經典方法、百分位法以及改進的PWM方法的優良性，得出改進的PWM方法具有更高的精度，并將該方法應用到導彈精度評定當中。

區間估計;Bootstrap方法;改進的PWM方法;導彈精度評定

一般武器系統研制周期比較長，試驗費用比較昂貴，且屬于消耗性試驗，得到的試驗數據是有限的。經典統計分析方法是建立在適量樣本基礎上的，在小樣本情形下，樣本均值易受異常點的影響，導致整個置信區間的穩健性受到影響，故精度不高。因此利用經典方法進行武器系統的試驗分析會存在不足。

目前，解決小樣本問題的方法主要有Bootstrap方法和Bayes方法［1－2］。其中，Bootstrap方法的基本思想都是通過再抽樣將小樣本轉化成大樣本;Bayes方法主要是有效地利用先驗信息。

PWM(投影深度加權平均)方法［3］是一種不依賴于總體分布的參數區間估計方法，通過合理引進深度函數和權函數，抑制異常點的影響。相同置信水平下，該方法得到的置信區間更短，但是PWM方法在小樣本下會出現溢出。

本文結合小樣本數據，引進一種新的導彈精度評定方法——改進的PWM方法［4］。經實測數據驗證，該方法具有較高的精度，能較好地應用到武器系統試驗分析中。由于該方法不依賴于總體分布，因此也可應用到其他工程的評定中(如產品的可靠性評估等)。

1 改進的PWM方法

小樣本下，改進的PWM方法的主要思想是借助Bootstrap抽樣方法［5］，將小樣本轉化成大樣本，再合理引進深度函數［6－8］和權函數［9－10］來抑制異常點的影響，通過百分位方法截取置信區間。在介紹改進的PWM方法之前，先介紹一下Bootstrap抽樣方法［11－14］。

設原始樣本為x1，x2，…，xn，Bootstrap抽樣方法有2種:

方法1

1)利用計算機在區間(0，M)(M＞＞n)內產生具有獨立性、滿周期性和均勻性的隨機整數η，n為所觀測樣本個數;

2)令j=η%n，j為n整除η得到的余數;

3)令i=j+1，x*=x(i)，其中x(i)是原始樣本x1，x2，…，xn按從小到大的排序后得到的第i個統計量，則x*即為所需的隨機樣本;

4)重復以上步驟n次，就得到一組再抽樣樣本x*=(x*1，x*2，…，x*n)。

方法2

1)利用計算機在區間(0，1)內產生隨機數η;

2)令β=(n－1)η，i=?β」+ 1;

3)令x*=x(i)+(β－i+1)(x(i+1)－x(i))，其中x(i)是原始樣本x1，x2，…，xn按從小到大的排序后得到的第i個統計量，則x*即為所需的隨機樣本;

通過數據模擬得到，第2種抽樣方法更接近于原總體分布，故本文采用第2種Bootstrap抽樣方法。文獻［13］證實了這種抽樣方法的可行性。

設樣本為x=(x1，x2，…，xn)，改進的PWM方法具體步驟如下:

其中m是{PD(xi，x)，(i=1，2，…，n)}的中位數。s≥1且k＞0是一個固定的正常數，它可以調節想要區分的具有不同投影深度的點的多少。本文中令s=2，k=3。

4)定義深度加權平均PWM

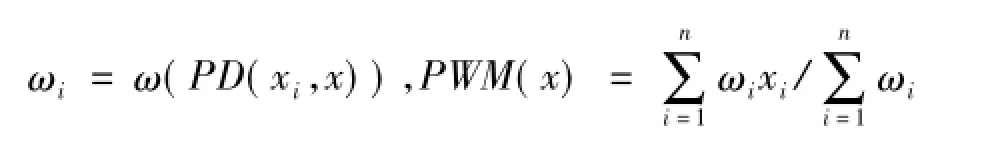
可以證明，PWM具有漸進正態性，并且PWM(x)→μ(n→∞)。

5)利用Bootstrap方法對原始樣本抽樣，得到M個樣本，對每一個樣本都按照以上4個步驟得到M個PWM值:PWM1，PWM2，…，PWMM，對這M個PWM值由小到大排序，得到PWM(1)，PWM(2)，…，PWM(M)，按照百分位法得到置信水平為1－α的置信區間是(PWM(Mα/2」+1)，PWM1－Mα/2」)。

2 通過數據模擬比較改進的PWM方法的優良性

本文分別取正態總體N(0，1)，泊松分布總體P(4)及指數分布總體Exp(1/4)。運用Matlab軟件進行模擬抽樣，令樣本數目分別為7，10和20，并且令Bootstrap抽樣次數M為500。程序運行一次得到的結果整理見表1。通過表1可以看出:在同一總體分布下，百分位方法比經典方法得到的置信區間長度更短;而相比之下，改進的PWM方法更好，得到的置信區間平均長度最短。

3 改進的PWM方法在導彈精度評定中的應用

精度評定［17－18］(包括射程評估、CEP評估、設計密集度評估等)是武器系統裝備實驗的重要內容，近年來，Bootstrap方法已應用到該領域。目前，我國戰略導彈的定型試驗僅為3～5發，在此小樣本下，很多方法都不適用。本文應用改進的PWM方法與傳統的方法及文獻［17］中的相關方法進行優良性的比較。

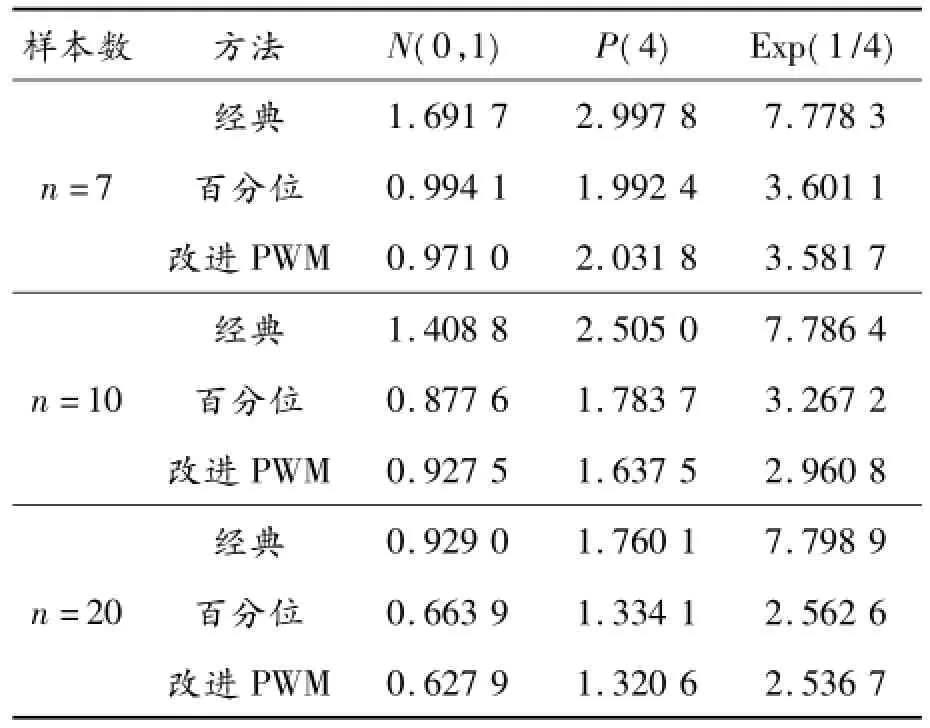
表1 3種方法下正態N(0，1)、泊松P(4)、指數Exp(1/4)分布的置信水平為95%的隨機模擬500次置信區間的平均長度

某型號導彈最大射程真實試驗數據為5 510，5 532，5 528，由正態分布N(5 520，102)產生。在改進前的型號做過的8次最遠射程試驗數據分別是:5 519，5 498，5 533，5 532，5 514，5 520，5 518和5 512，由正態分布N(5 515，122)產生，單位為公里。Bootstrap抽樣1 000次，計算射程均值的80%置信區間，比較結果見表2。

通過表2可以看出:上述5種區間估計方法均包含了真值，在相同置信水平下，本文中改進的PWM方法得到的導彈精度評定結果精度更高;在不考慮驗前信息和考慮驗前信息2種情況下，得到的置信區間長度分別最短;考慮驗前信息的數Bootstrap方法計算出的置信區間長度已經遠遠小于經典方法和不考慮驗前信息的Bootstrap方法;而在改進的PWM方法下，考慮驗前信息情形下得到的置信區間遠遠小于其他4種方法得到的置信區間。因此，改進的PWM方法可以很好地應用到武器系統裝備實驗的精度評定當中。

表2 導彈射程精度評定結果

4 結束語

本文通過改進PWM區間估計方法，比較了正態分布、泊松分布以及指數分布下的均值區間估計方法的優良性。通過計算機數據模擬以及在導彈射程精度評定中的應用得出結論:改進的PWM方法具有更高的精度;相同置信水平下得到的置信區間的平均長度更短;改進的PWM方法不依賴于總體分布。因此，該方法能很好地應用到武器系統裝備評定等其他小樣本估計問題的工程領域中。

［1］樊立明，吳鵬，萬偉.基于Bayes自助法的小子樣命中精度評估［C］//Proceedings of 2010 The 3rd International Conference on Computational Intelligence and Industrial Application.USA:［s.n.］，2010.

［2］李靜，馮志剛.隨機加權最大熵法在可靠性評估中的運用［J］.可靠性與環境適應性理論研究，2008，26 (6):62－65.

［3］Yijun Zuo.Is the t confidence interval:±tα(n－1)s/optimal?［J］.The American Statistician，2010，64 (2):170－173.

［4］相榮霞，袁永生，戴啟璠.改進的PWM方法及小樣本下的穩健區間估計［J］.曲阜師范大學學報，2012，38 (4):25－27.

［5］Bradley Efron.Second Thoughts on the Bootstrap［J］.Statistical Science，2003，18(2):135－140.

［6］Yijun Zuo.Data Depth Trimming Counterpart of the Classical t(or T2)Procedure［J］.Journal of Probability and Statistics，2009，19:1－9.

［7］李強.兩類數據深度及深度加權M估計［D］.長沙:國防科學技術大學，2008.

［8］范允征，林路.穩健的深度加權小波估計［J］.南通大學學報:自然科學版，2008，7(4):78－81.

［9］范允征，林路.線性回歸模型的深度加權最小二乘估計和擬合檢驗［J］.南京師范大學學報:自然科學版，2008，31(3):39－43.

［10］Yijun Zuo，Robert Serfling.General Notation of Statistical Depth Function［J］.The annals of Statistics，2000，28(2) :461－482.

［11］Thomas J.DiCiccio，Bradley Efron.Bootstrap Confidence Intervals［J］.Statistical Science，1996，11(3):189－228.

［12］扎庫拉.戈文達拉玉盧.抽樣理論與方法(英文版)［M］.北京:機械工業出版，2005.

［13］張守玉，封偉書.基于Bootstrap方法的正態分布樣本數據生成研究［J］.裝配指揮技術學院學報，2009，20 (2):97－100.

［14］曹欣，孫新利，李振.改進灰自助法及其在可靠性評定中的應用［J］.山東大學學報:工學版，2010，40(1): 144－148.

［15］卯詩松，程依明，濮曉龍.概率論與數理統計教程［M］.北京:高等教育出版社，2006.

［16］夏樂天，郭寶才，肖艷文.指數分布參數置信區間的最短化研究［J］.河海大學學報:自然科學版，2003，31 (3):354－357.

［17］胡正東，曹淵等.特小子樣試驗下導彈精度評定的Bootstrap方法［J］.系統工程與電子技術，2008，30 (8):1493－1497.

［18］李書進，鈴木祥之.基于Bootstrap濾波的非線性系統的識別［J］.武漢理工大學學報，2003，25(5):30－32.

(責任編輯 劉舸)

Improved PWM Method under Small Sample and Its Application on Missile Precision Evaluation

LYU Peng1，YUAN Yong－sheng1，XIANG Rong－xia1，DAI Qi－pan2
(1.College of Science，Hohai University，Nanjing 210098，China;
2.Administration Office of Irrigation in Jiangsu Province，Huai’an 223200，China)

It is inadequate to analyze the data of small sample with classical statistical method in experiment of weapon system.Based on the characteristics of small sample，this paper firstly introduces the improved PWM interval estimation methods reasonably，then compared the classical method，bootstrap percentile CI method and the improved PWM method through data simulation respectively in normal distribution，Poisson distribution and exponential distribution.The result shows that the improved PWM method is more efficient.Finally，we applies this method to the missile precision evaluation.

interval estimation;Bootstrap method;improved PWM method;missile precision evaluation

O212

A

1674－8425(2014)05－0139－04

10.3969/j.issn.1674－8425(z).2014.05.026

2013－10－22

江蘇省水利科技創新基金資助項目(2011059);河海大學自然科學基金資助項目(2009426311)

呂鵬(1990—)，男，山東青島人，碩士研究生，主要從事小樣本理論及其應用研究。

呂鵬，袁永生，相榮霞，等.小樣本下改進的PWM方法及其在導彈精度評定中的應用［J］.重慶理工大學學報:自然科學版，2014(5):139－142.

format:LYU Peng，YUAN Yong－sheng，XIANG Rong－xia，et al.Improved PWM Method under Small Sample and Its Application on Missile Precision Evaluation［J］.Journal of Chongqing University of Technology:Natural Science，2014(5):139－142.