基于優化的GM(1,1)模型在高速公路沉降預報中的應用
張非非,胡 健,佘兆宇
(江蘇現代路橋有限責任公司,江蘇南京 210049)
基于優化的GM(1,1)模型在高速公路沉降預報中的應用
張非非?,胡 健,佘兆宇
(江蘇現代路橋有限責任公司,江蘇南京 210049)
GM(1,1)模型是最常見的灰色系統模型,也是預測理論體系中的一個重要分支,被廣泛應用于各種建筑物、構造物的變形監測預報中。本文針對傳統GM(1,1)模型中存在的問題,對模型中的初始值、背景值及時間響應函數進行優化,得到一個優化的GM(1,1)模型,并將其應用到高速公路的沉降預報。實例證實,優化的GM(1,1)模型的模擬和預報精度比傳統GM(1,1)模型有顯著提高,體現了該模型的優良性與適用性。
GM(1,1)模型;初始值;背景值;時間響應函數;沉降預報
1 引 言
在修建與維護高速公路中,沉降監測是判斷路面高程變化及其平整度和穩定性的重要手段。沉降預報是沉降監測數據處理的重要組成部分,常用的沉降預報模型有回歸分析、人工神經網絡、時間序列分析、灰色系統模型等。其中,灰色系統模型能夠根據少量已知信息進行建模和預報,且建模簡單,預報精度高,被廣泛地應用于各個領域中,GM(1,1)模型是最常用的灰色系統模型[1~3]。
傳統GM(1,1)模型成功地應用到諸多工程的沉降預報中,但同時也出現一些預報精度不高的情況,所以有必要對GM(1,1)模型進行優化[4]。本文分析了傳統GM(1,1)模型中存在的不足,對模型中的初始值、背景值及時間響應函數進行優化,構成優化的GM (1,1)模型。通過實例,將傳統GM(1,1)模型和優化的GM(1,1)模型分別應用到高速公路的沉降預報中,并比較二者的預報精度。
2 傳統GM(1,1)模型
2.1 建模步驟[5~7]
(1)給定原始觀測序列,記為:
X(0)={x(0)(1),x(0)(2),…x(0)(n)}
(2)對上式進行一階累加,生成1-AGO序列,記為: X(1)={x(1)(1),x(1)(2),…x(1)(n)},公式表示如下:
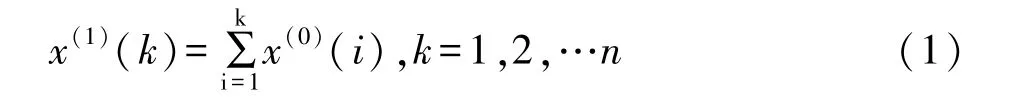
(3)進行準光滑性檢驗、準指數規律檢驗:


當ρ(k)<0.5且σ(1)(k)∈[1,1.5]時,則X(0)滿足準光滑、準指數規律條件,可以使用GM(1,1)模型建模。
(4)生成緊鄰均值序列,又稱為背景值序列,記為:Z(1)={z(1)(1),z(1)(2),…z(1)(n),公式表示如下:

其中參數a反映了系統發展的態勢,稱為發展系數;b是反映數據變化的關系,稱為灰色作用量。根據最小二乘原理,解該白化微分方程,可得到時間相應函數為:

(6)進行累減還原序列為:

2.2 模型精度評定
(1)計算模型殘差:
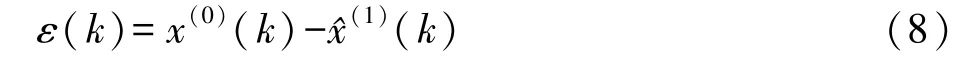
(2)計算原始觀測序列X(0)的均值ˉx和方差:
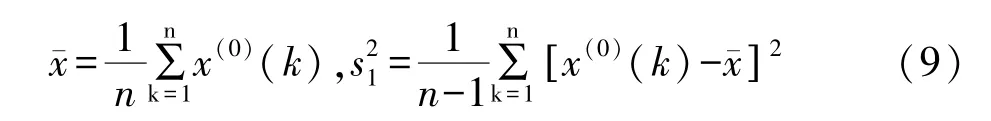
(3)計算模型殘差的均值ˉε和方差s22:
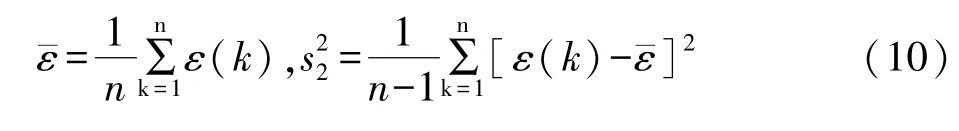
(4)計算后驗方差比值c和小誤差概率p:
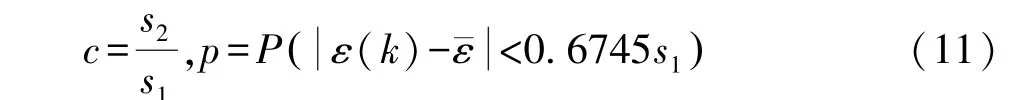
當后驗方差比值c<0.35,且小誤差概率p>0.95時,傳統GM(1,1)模型的預報精度良好。
3 優化的GM(1,1)模型
當序列數據變化急劇(高增長指數情況)時,若直接采用傳統GM(1,1)模型往往會產生較大滯后誤差,模型偏差較大。近年來,很多學者從不同的方面進行GM(1,1)模型優化,來提高建模精度。本文提出對模型的初始值、背景值及時間響應函數進行優化并相結合的方法,得到優化的GM(1,1)模型。
優化的GM(1,1)模型的建模步驟如下:
(1)給定原始觀測序列X(0);
(2)對上式進行一階累加,生成1-AGO序列X(1);
(3)對模型的初始值進行優化,使X(1)所有分量的擬合誤差平方和S最小,即:

則模型的初始值可優化為:

(4)生成優化的背景值序列Z(1):
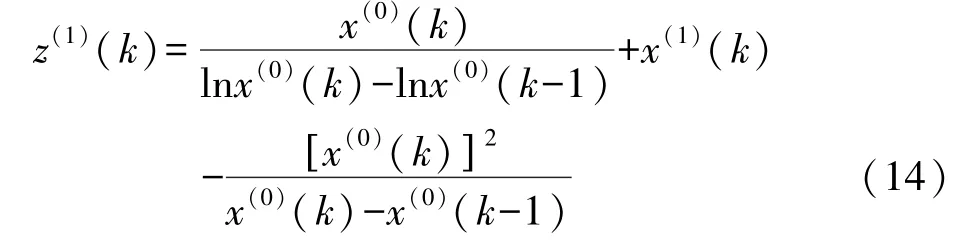
其中,當x(0)(k)=x(0)(k-1)時,z(1)(k)=x(1)(k)。
(5)生成優化的時間相應函數:

4 實例計算
以連云港某段高速公路的修建和運營階段的沉降觀測為例,出于工程安全考慮,我們對其進行了長期沉降監測。在修建階段(1期~40期)中,由于施工條件限制,觀測數據浮動較大,變化急劇;而在運營階段(41期~60期)中,觀測數據浮動較小,監測點較為穩定。
采用Matlab軟件建立傳統GM(1,1)模型與優化的GM(1,1)模型算法,選取#J01監測點在修建階段1期~35期與在運營階段41期~55期的高程觀測值為原始觀測序列,分別采用傳統GM(1,1)模型與優化的GM(1,1)模型預報36期~40期、56期~60期的高程值,并與實測序列進行對比分析。
由圖1可知,對于高速公路修建階段中,數據變化急劇,累計沉降達到90 mm,使用優化的GM(1,1)模型的高程值模擬和沉降預報效果均優于傳統GM(1, 1)模型。由表1可知,在修建階段中,使用優化的GM (1,1)模型有較好地可靠度和精度。
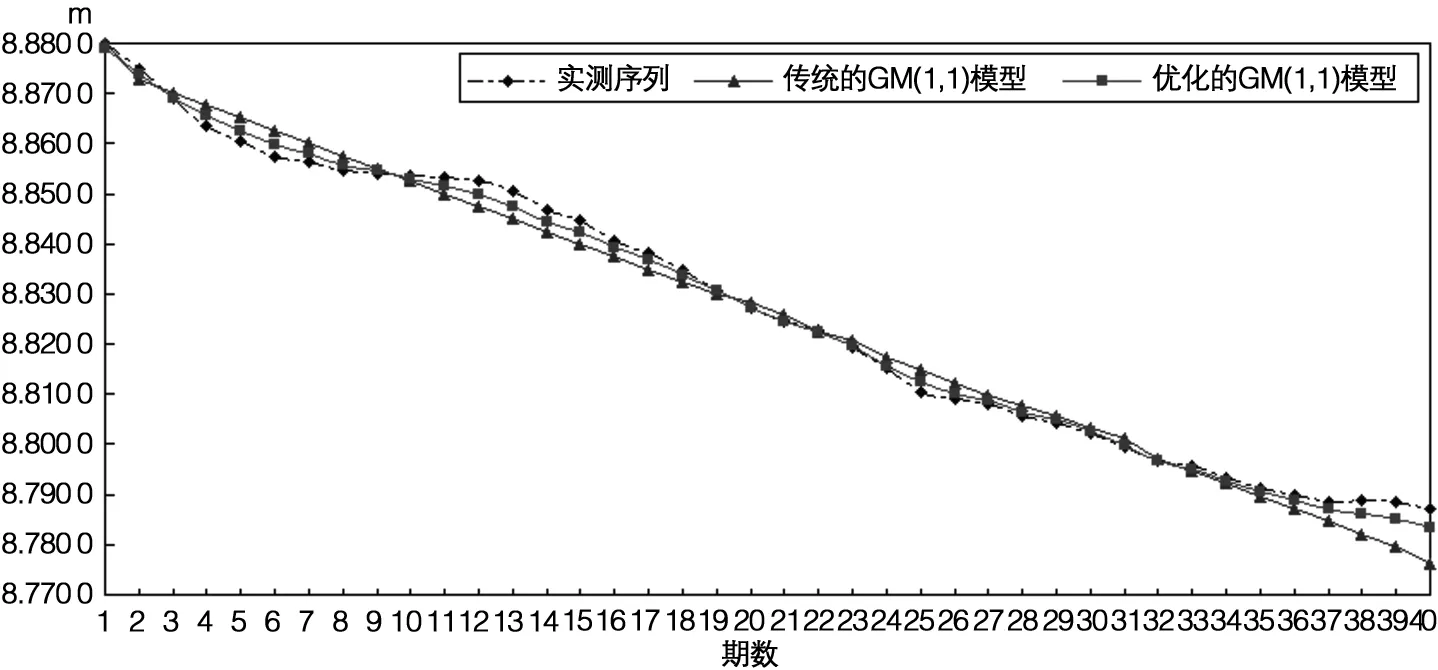
圖1 #J01監測點的沉降預報(修建階段)

表1 修建階段兩種模型沉降預報精度評價指標

表2 運營階段兩種模型沉降預報精度評價指標
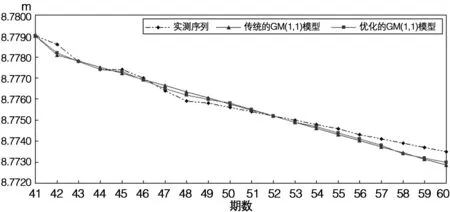
圖2 #J01監測點沉降預報(運營階段)
由圖2和表2可知,對于高速公路運營階段中,數據較為平穩,累計沉降為6 mm,變形量較小,使用優化的GM(1,1)模型與傳統GM(1,1)模型的高程值模擬和沉降預報效果均良好,二者可靠度和精度也相當。
5 結 語
本文通過傳統GM(1,1)模型的研究,提出了對模型中的初始值、背景值及時間響應函數進行改進的優化的GM(1,1)模型,并將該模型應用到高速公路的沉降預報。實例結果表明,優化的GM(1,1)模型對于數據變化急劇的原始觀測序列的模擬和預報具有較好地優良性和適用性,對于數據變化平穩的原始觀測序列的模擬和預報精度則與傳統GM(1,1)模型相當。
[1] 劉思峰,黨耀國,方志耕.灰色系統理論及其應用[M].北京:科學出版社,2010.
[2] 陳剛,王波,鄧哲.GM(1,1)模型在建筑物沉降預測中的應用及Matlab的實現[J].城市勘測,2011(1):107~109.
[3] 蘭孝奇,嚴紅萍,劉精攀.灰色系統預測模型在沉降監測中的應用[J].現代測繪,2006,29(1):24~26.
[4] 李偉,袁亞南,牛東曉.基于緩沖算子和時間響應函數優化灰色模型的中長期負荷預測[J].電力系統保護與控制,2011,39(10):59~63.
[5] 何霞,劉衛鋒.一個基于背景值和初始條件優化的GM (1,1)模型[J].河南科學,2011,29(3):260~263.
[6] 鄭雪琴,秦棟.系統優化的GM(1,1)模型在大壩位移預測中的應用[J].水電能源科學,2011,29(4):75~77.
[7] 何勇剛,周步祥.緩沖算子改進灰色模型在中長期負荷預測中的應用[J].四川電力技術,2007,30(2):5~7.
[8] 謝正文,胡漢華,胡毅夫.改進GM(1,1)模型在路基沉降預測中的應用[J].巖土力學,2005,26(10):227~230.
The Application of The Optimized GM(1,1)Model in Settlement Forecast of Express Highway
Zhang Feifei,Hu Jian,She Zhaoyu
(Jiangsu Modern Highway Bridge Co.Ltd,Nanjing 210049,China)
GM(1,1)mode is the most common content of grey system theory.And it is also an important branch of forecasting theories.The model is used to forecast the deformation of building widely.According to the problems of the traditional GM(1,1)model,the initial value,background value and time response sequence were optimized firstly.The optimized GM(1,1)model was applied to the settlement forecast of express highway.Through the example,the results show that the optimized GM(1,1)model has a very high fitting and prediction precision than the traditional model.
GM(1,1)model;initial value;background value;time response sequence;settlement forecast
2013—08—21
張非非(1974—),男,工程師,主要從事道路橋梁檢測研究工作。

