基于UMAC 的超精密研磨拋光機工件坐標系的建立

陳 琦

(中國科學院 長春光學精密機械與物理研究所，長春 130033)

0 引言

由于研制超精密陶瓷導軌的需要，本文用自主研發的超精密導軌研磨拋光機來實現對其加工。在陶瓷導軌后續超精密加工過程中需要頻繁檢測和研拋，由于陶瓷導軌工件的質量較大，在研磨拋光機和平面干涉儀之間來回搬動工件的過程中，陶瓷導軌在研磨拋光機上的每次定位很難保證完全一致。如果研磨拋光機基于機床坐標系來加工陶瓷工件的話，其定位精度不高。

現在對于開放式數控系統的研究越來越多［1-4］，加工的對象也是多種多樣，對于某些特定的加工對象，基于機床坐標系的加工方式不能夠完全滿足要求，因此對于工件坐標系的研究與設計很有必要［5-10］。超精密導軌研磨拋光機數控系統基于UMAC 控制器，針對陶瓷導軌這種加工對象，采用基于機床坐標系與工件坐標系相結合的辦法來實現運動控制。UMAC 控制器對于機床坐標系的建立相對容易，本文主要探討UMAC控制器中工件坐標系的建立［11］。

1 UMAC 坐標系統

UMAC 中的坐標系統是一組(一個或更多)電機之間的同步運動。軸是坐標系統中的一個元素，通過使用比例因子和偏移量把它指派到一個電機上來實現。可命名的軸名稱有直角坐標軸［X，Y，Z］、［U，V，W］和旋轉軸［A，B，C］。一個坐標系統通過使用軸定義指令來建立，一個軸通過指派一個或多個電機來定義，電機映射到軸可以有比例因子也可以有原點偏移，比例因子代表每個單元多少編碼器計數值。例如:#1→1000X +500 ，其中#1 代表1 號電機，1000 是比例因子，單位是counts/user unit，500 是偏移量，單位是counts。

在實際應用中，通過這種方法可以建立研磨拋光機的機床坐標系，由下式表示:

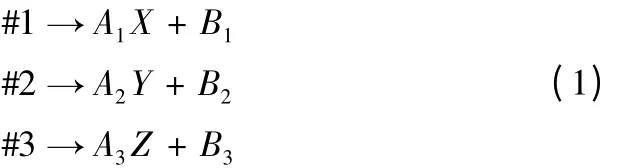
其中A1到A3是比例因子，B1到B3是偏移，#1 到#3 分別代表1～3 號電機。

2 坐標系轉換

不同空間直角坐標系之間進行轉換時，如圖1 所示，當兩個空間直角坐標系轉換既有旋轉又有平移時，則存在三個平移參數和三個旋轉參數，再加上兩個坐標系尺度變化參數m，總共有七個參數。相應的坐標變換公式為:

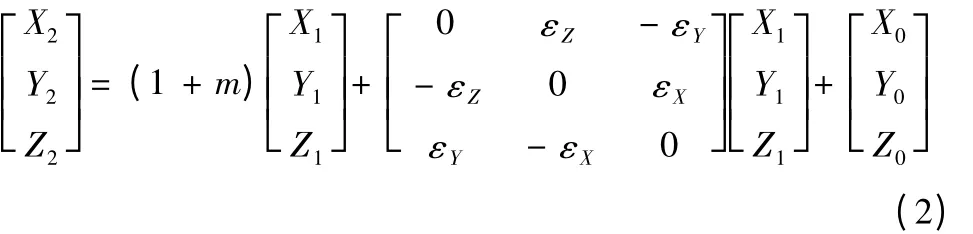
式(2)為兩個不同空間直角坐標系之間的轉換模型，其中含有7 個轉換參數，為了求得7 個轉換參數，至少需要3 個公共點，當多于3 個公共點時，可按最小二乘法求得各參數的最合適值。

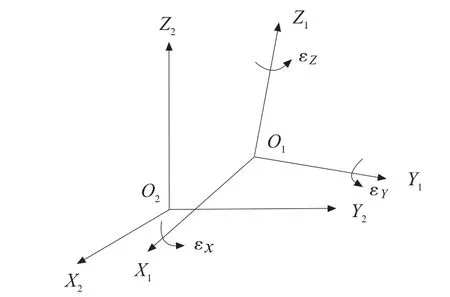
圖1 不同空間直角坐標系之間轉換

3 工件坐標系的建立

對于電機與直角坐標軸不完全一一對應的話，在UMAC 控制器中建立坐標系時，直角坐標軸可以是電機的線性組合，由下式表示:

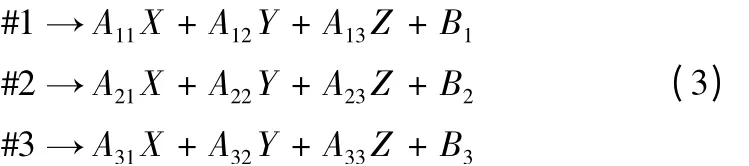
其中A11到A33是比例因子，B1到B3是偏移，#1 到#3 分別代表1～3 號電機。

研磨拋光機在實際應用過程中，首先采集工件坐標系中的三個特定點:原點O、X軸正向一點和XOY平面第一象限任意一點，通過原點O和X軸正向一點來確定X向的單位向量，然后結合XOY 平面第一象限任意一點來確定Y向的單位向量，最后通過X向、Y向和Z向三個單位向量的正交性來確定Z向的單位向量。

設采集的原點O為P1(x1，y1，z1)，采集的X軸正向一點為P2(x2，y2，z2)，采集的XOY 平面第一象限任意 一 點 為P3(x3，y3，z3)，設 點P1(x1，y1，z1)和 點P2(x2，y2，z2) 的 距 離 為OX， 得OX=設點P1(x1，y1，z1)和 點P3(x3，y3，z3)的 距 離 為OY，得OY =

由原點P1(x1，y1，z1)和X軸正向一點P2(x2，y2，z2)來確定X向的單位向量i=(ix，iy，iz)，得:

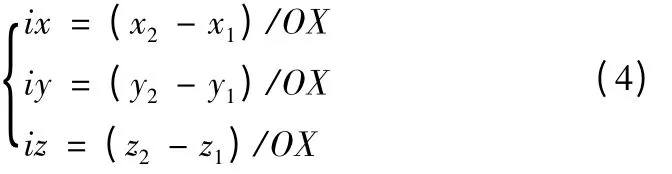
設P1P2和P1P3的夾角∠P2P1P3為∠XOY，結合XOY平面第一象限任意一點P3(x3，y3，z3)來確定Y向的單位向量j=(jx，jy，jz)，得:

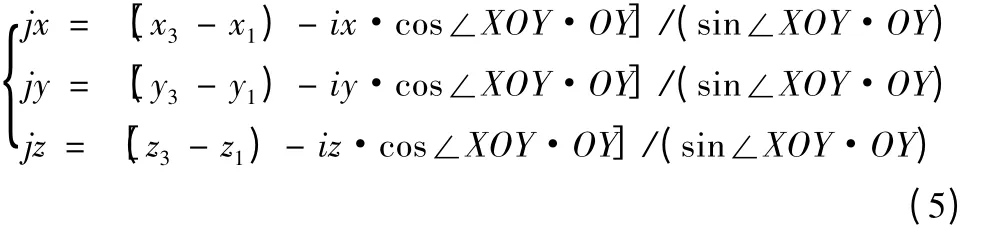
其中，

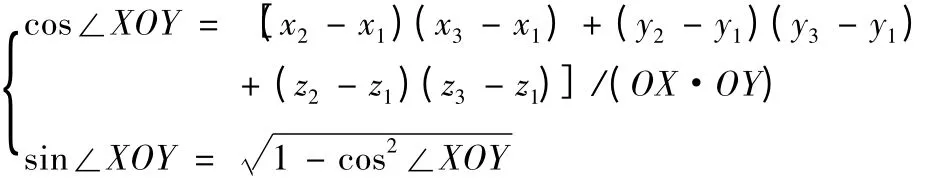
通過三個單位向量的正交性k=i·j 來確定Z向的單位向量k=(kx，ky，kz)，得

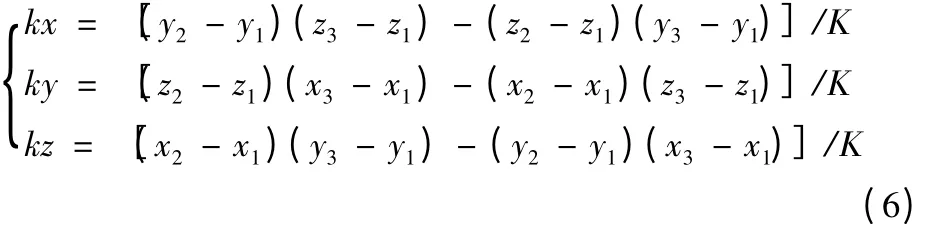
其中，

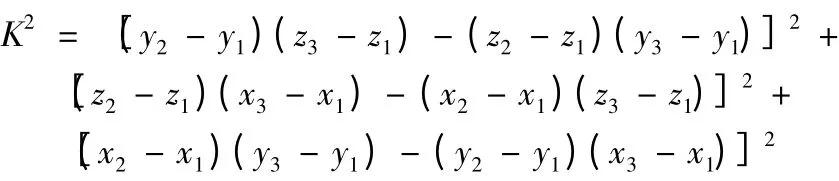
設陶瓷導軌上基于工件坐標系的某一點Pn的坐標為Pn(xn，yn，zn)，其在機床坐標系上的坐標為P'n(x'n，y'n，z'n)，兩者之間關系如下:

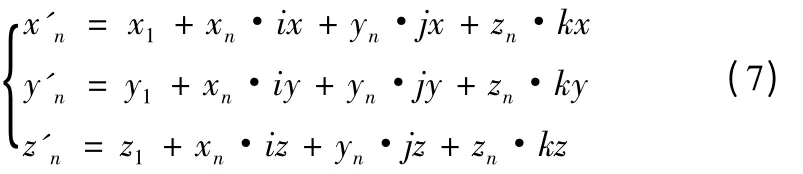
由此實現了陶瓷導軌上某點從工件坐標系到機床坐標系的轉換。

研磨拋光機軟件坐標轉換模塊如圖2 所示，移動相關的軸使拋光頭到達指定位置，分別點擊軟件界面中［取原點］、［X正向一點］和［XY面一點］，其三點的坐標值顯示在左側“工件坐標系”對應的數據框中，點擊［計算單位向量］，計算出工件坐標系的單位向量，并顯示在左側“工件坐標系”對應的數據框中，在左側“坐標系轉換”中可以實現工件坐標系和機床坐標系的相互轉換，輸入工件坐標系各個坐標值，點擊［工件→機床］，則機床坐標系顯示出其對應的坐標值，輸入機床坐標系各個坐標值，點擊［機床→工件］，則工件坐標系顯示出其對應的坐標值。

在實際應用過程中，當點擊完界面中［取原點］、［X正向一點］和［XY面一點］確定好對應的三點后，點擊［解坐標系］進行單位向量的計算，然后點擊［打開數據］，該原始數據是基于工件坐標系的坐標值，直接把原始數據進行坐標轉換，轉換完后直接點擊［下載運行］即可。

4 結束語

本文研制的研磨拋光機在實際應用過程中，首先采集陶瓷導軌在工件坐標系中的三個特定點:原點O、X軸正向一點和XOY 平面第一象限任意一點，通過這三個特定點正確的解算出工件坐標系與機床坐標系之間的轉換關系。與公式(2)相比較，只需要采集三個點就能把機床坐標系轉換成工件直角坐標系，非常實用和方便;而且不需要用最小二乘法求得各參數的最合適值，該方法計算值準確。若安裝誤差等原因導致研磨拋光機坐標軸的正交性不準確，采用該方法建立的工件坐標系不受其影響。該方法也適合應用在其他相關場合。

［1］彭玉海，白海清，何寧. 基于PMAC 運動控制卡的多軸開放式數控系統開發［J］. 機床與液壓，2008，36(8):255 -257，251.

［2］尚純，崔寶磊，楊光，等. 基于PMAC 的激光加工機床開放式數控系統開發［J］. 機床與液壓，2013，41(19):83-85，124.

［3］李淑萍，張筱云. 基于PMAC 的開放式數控系統研究與應用［J］. 微電機，2009，42(7):65 -68，90.

［4］邴龍健，雷玉勇，蔡黎明，等. 基于PMAC 控制器的開放式數控系統研究［J］. 制造技術與機床，2009 (6):20-23.

［5］熊顯文，明興祖. 數控加工中心工件坐標系的建立［J］.組合機床與自動化加工技術，2003(12):69 -72.

［6］陳銀清. 數控加工中工件坐標系的建立及其對刀技巧［J］. 煤礦機械，2004(4):78 -80.

［7］楊靜云，李良仁. 數控加工中對刀設定工件坐標系的控制方法［J］. 組合機床與自動化加工技術，2009(5):72-74.

［8］祁型虹，熊顯文，黃浙英. 建立數控工件坐標系的方法綜述［J］. 機械設計與研究，2006，22(2):75 -78.

［9］張亞萍，曹燕. 三點圓法實現工件坐標系的自動設定［J］. 組合機床與自動化加工技術，2009(6):91 -92.

［10］劉源，韓振宇，王永章，等. 可配置型五坐標B 樣條插補控制器的研制［J］. 光學精密工程，2010，18(7):1577-1585.

［11］劉恒麗，王太勇，王冬，等. 基于PMAC 的數控系統工件坐標系的設定方法分析［J］. 制造業自動化，2013，35(6):138 -140.