基于二階統計量的相關信源盲均衡與辨識算法研究
陳靜
基于二階統計量的相關信源盲均衡與辨識算法研究
陳靜
內蒙古科技大學包頭師范學院,內蒙古包頭014030
本文給出了一種基于二階統計量的相關信源盲均衡與辨識算法,應用接收信號的自相關矩陣將信道參數估計問題轉化為與自相關矩陣有關的特征向量求解問題。仿真結果表明該算法對輸入為相關信源的信道辨識與均衡具有較好的效果,只用較短的觀察數據就可以完成系統的辨識,二階算法運算量明顯減小,且有效地降低了碼間干擾。
盲均衡;盲辨識;過采樣;前向線性預測誤差;二階統計量
盲信道辨識與均衡[1,2]在通信和信號處理領域已經受到普遍關注,成為通信信號處理中的關鍵技術,傳統的盲均衡都是基于高階統計量方法。本文主要圍繞Tong[3]等人的算法,即基于二階統計量的盲均衡算法來實現的,但其算法適用于獨立同分布的非相關信源,如果是相關信源該算法就不能有效地均衡信道。由于其算法的局限性,本文將輸入信源的條件放寬:假設輸入信號是一個零均值的相關序列,這一假設使得算法對輸入信號的要求大大降低。
1 算法實現的條件
假設輸入信號有一定的的自相關性,輸入信號是比較實際的相關信源。本文的假設條件為:
假設1:信道沖激響應{hi( k)}的Z變換Hi( Z)沒有公共零點,最大階數為Lh。
假設2:噪聲n(t)是方差為σn2均值為零的平穩白噪聲且與信號序列不相關。
假設3:輸入信號是平穩相關序列s(i)
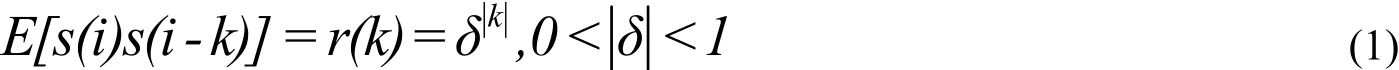
信道為FIR SIMO模型[4],SIMO模型可以通過設置多個傳感器或對SISO進行過采樣得到。先對FIR SIMO輸出結果分析:

{an}:是零均值,廣義平穩輸入序列;xn, hn,wn是p× 1維向量,分別是信道輸出向量,信道沖擊響應和白噪聲。信道為FIR SIMO模型[4],SIMO模型可以通過設置多個傳感器或對SISO進行過采樣得到。方程(2)可以寫成如下的關系式[3]:

H是P( N+1)×(L+N +1)矩陣:

2 輸入為相關信源的盲均衡與辨識算法
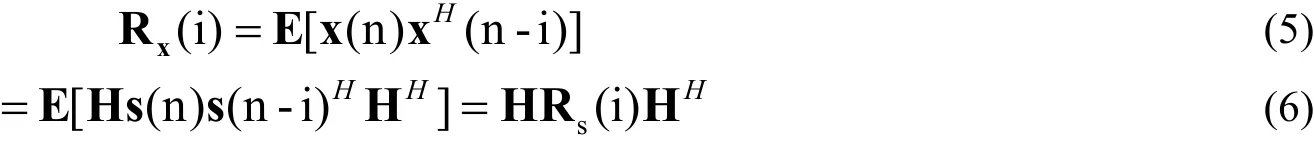
我們希望能夠通過i=0,1時,根據Rs(0),Rs(1)來尋找(3)式的H矩陣。Rs(0)是對稱Toeplitz矩陣,我們可以對其進行Cholesky分解,獲得下三角矩陣L,同時HL=。

那么
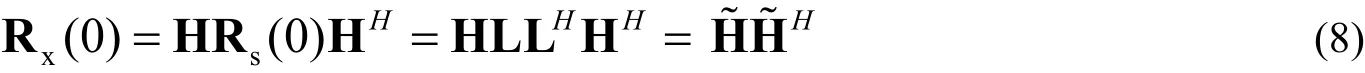
有
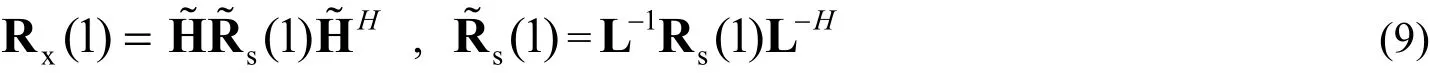
觀察s(0)R,s(1)R可知,s(1)R的后d-1行與s(0)R的前d-1行相同,或者說s(1)R的前d-1行與

即:

參考d階前向預測誤差濾波器的增廣維納-霍夫方程[6]:

其中0是d 1×維零向量。s(0)R是抽頭輸入的相關矩陣,dP前向預測器的最小均方誤差,fw為抽頭權向量[wf,1,wf,2,…,wf,d]T,其中我們設0<wf,d<1。由(12)式可得r+Rs(0)wf=0,,前向線性預測誤差濾波器的系數可由上式得出:,那么:
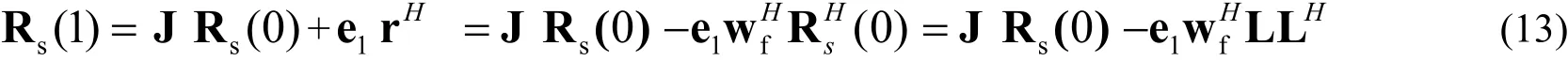
將(13)帶入(9)式可得:
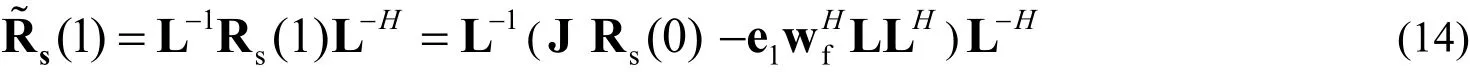
對Rx(0)進行奇異值分解得:Rx(0)=UdΔ2UdH,即:
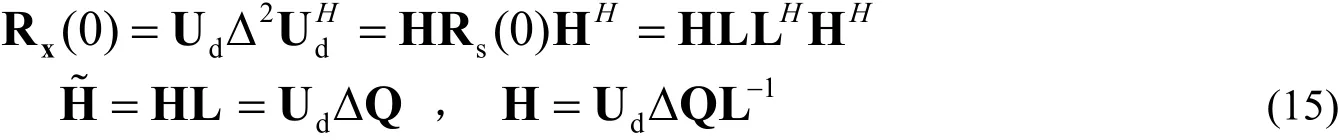
對Rx(1)兩邊分別乘以,同時帶入(16)式得:
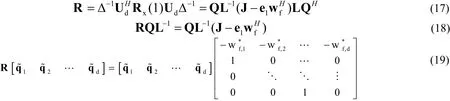
得方程組:


可以將J-e1wfH分解為矩陣乘積的形式,

現在考慮將式(22)式等式右邊部分化簡為R的奇異值分解形式,我們將下三角矩陣L的主對角線元素設為:{α1, α2,…,αd}
并令

通過觀察,我們發現(22)式中D× L就相當于D乘以L的主對角線元素{α1, α2,…,αd},即得到了下式:
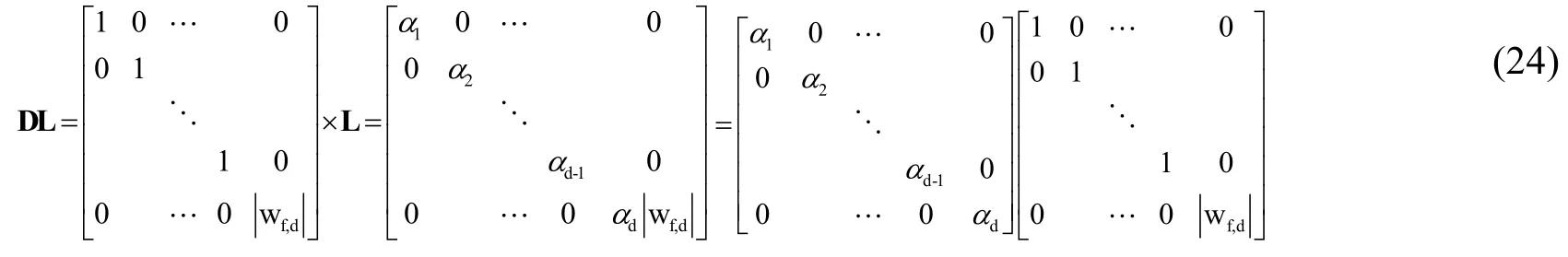
因為是對角陣,所以系數{α1, α2,…,αd}可以提出來那么

上式相當于對R進行奇異值分解:R=UΛVH,其中D相當于Λ,為對角陣。U=QM。因此可得Q對應的列向量{q1, q2,…,qd}即是R奇異值分解對應的右特征向量V對應的列向量。因為0<wf,d<1,所以我們令qd為wf,d對應的特征向量,近似可取qd為R奇異值分解最小特征值對應的特征向量。下面我們的任務是求解Q~陣對應的其他向量,由于我們已知:
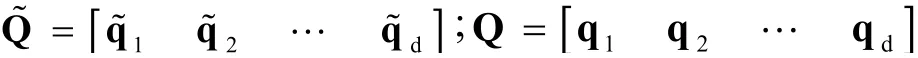
且:

由于Rs(0)=LLH,L為下三角矩陣,那么L-1仍為一對應的的下三角矩陣,那么L-1的最后一列為:

將qd帶入(27)式即可求解得到,將帶入式(26)就求出的所有列向量…]。將求出的Q帶入下式得信道估計H'

從而恢復出發射信號:

3 基于MATLAB的算法仿真
為了比較本文算法與Tong算法的性能差別,進行了兩組信道仿真實驗。定義信噪比函數如下:
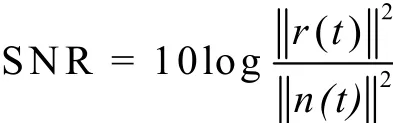
為了衡量算法的性能,定義如下歸一化均方根誤差函數(NRMSE):
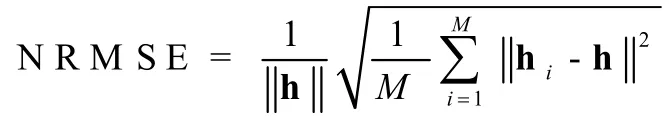
其中,M為Monte Carlo實驗次數,本文取20;h為真實信道沖擊響應向量;ih為第i次實驗估計出的信道沖擊響應向量。仿真中輸入信號是一階Markov信源[7],其轉移矩陣由下表給出:

表1 Markov信源轉移特性Table 1 Transfer characteristics of Markov signal
3.1仿真1
采用文獻[3][6]的信道,形式如下:
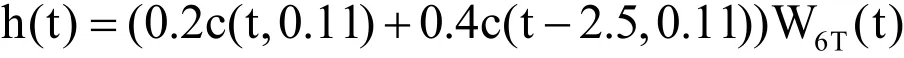
式中c(t-t0,β)是升余弦沖擊響應,滾降因子為β,時間延遲為t0。在Matlab中,我們選用的函數名為:rcosfir函數。6TW(t)是矩形窗函數,間隔為6倍碼元間隔。我們對輸出信號以輸入信號的4倍采樣率采樣。由圖1(b)可以看出,該信道23個零點中有21個位于單位圓外,因此是一個非最小相位系統,較難均衡。
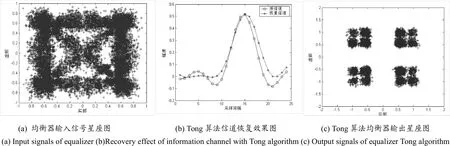
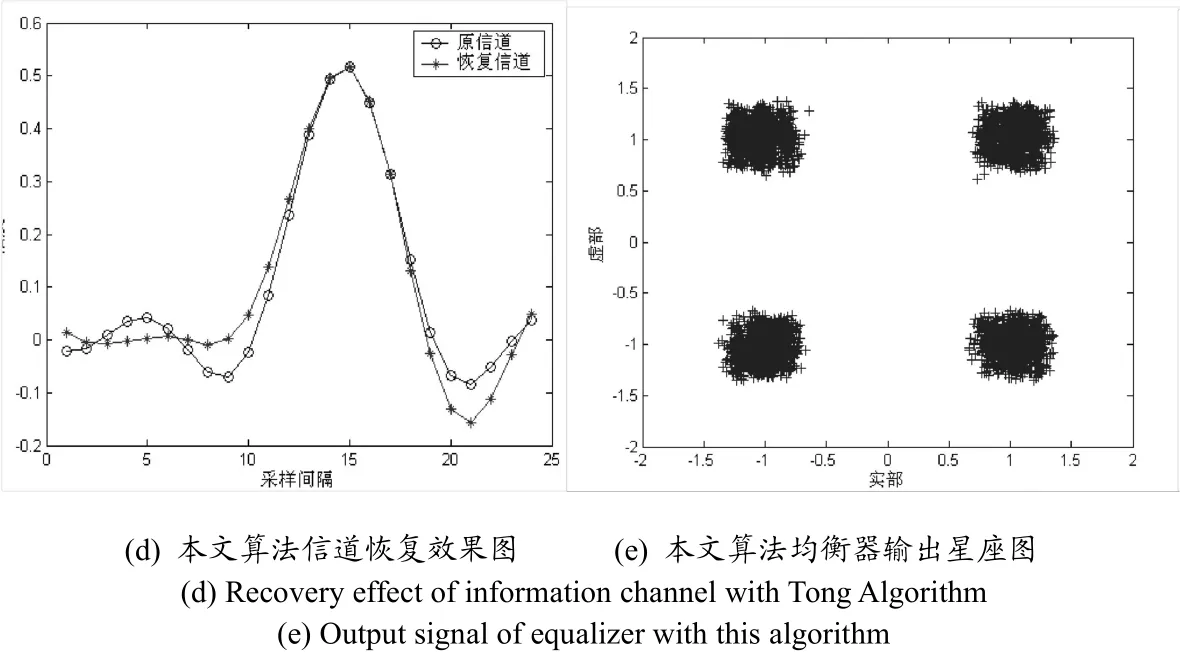
圖2 (a-e)信噪比為30 dB時算法性能比較Fig.2 Comparison among properties when signal noise ratio 30 dB in a-e
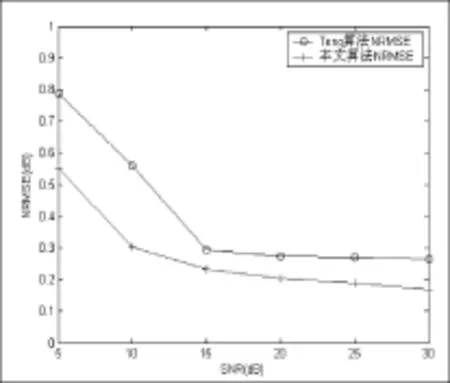
圖3 Tong算法與本文算法剩余NRMSE比較Fig.3 Comparison of odd NRMSE between Tong and this algotithm
由圖(2)可以看出,本文算法相對于Tong算法在輸入為相關信源時,能夠更好地辨識信道,均衡器輸出信號星座圖更加緊密,因此有利于提高均衡器的判決性能。
3.2仿真2

采用文獻[8]的4倍過采樣信道,信道沖擊響應為:
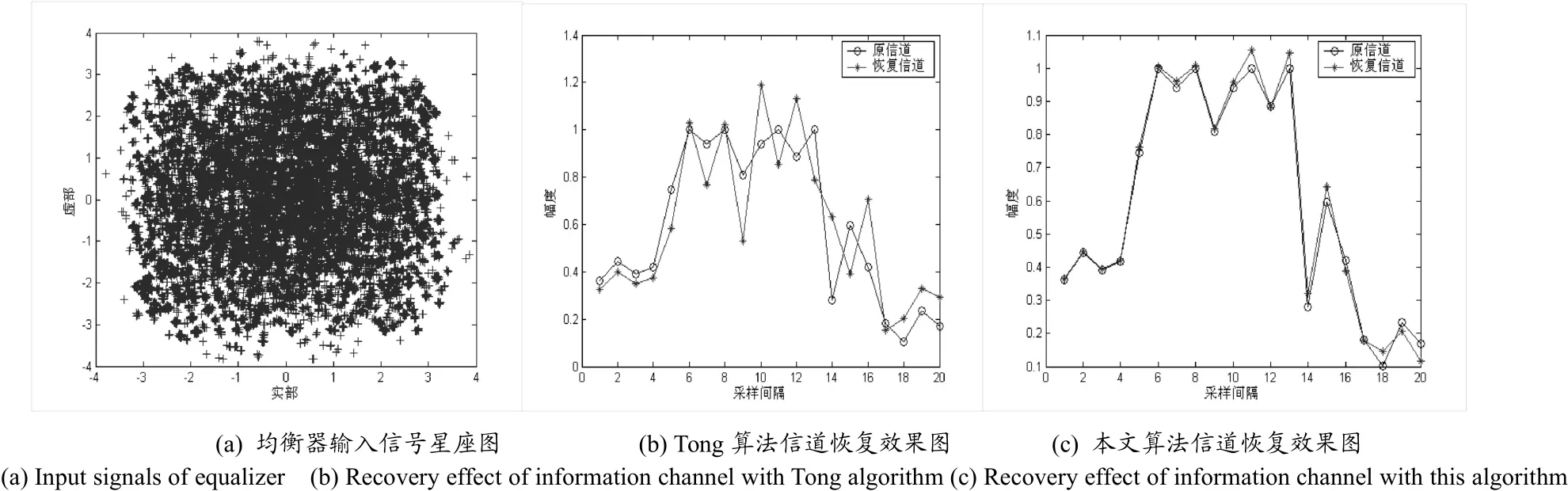
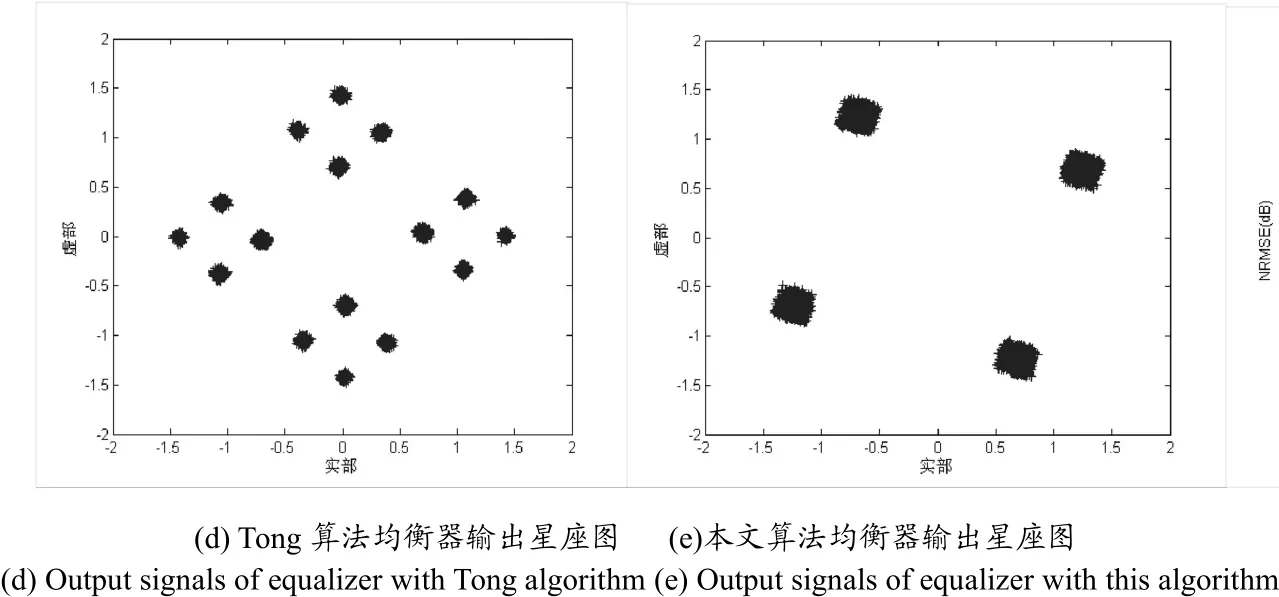
圖4 (a-e)信噪比為30 dB時算法性能比較Fig.4 Comparison among properties when information noise ratio 30 dB in a-e
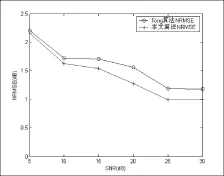
圖5 Tong算法與本文算法剩余NRMSE比較Fig.5 Comparison of odd NRMSE between Tong and this algorithm
由圖(4)可以看出,本文算法相對于Tong算法在輸入為相關信源時,能夠更好地辨識道,均衡器輸出信號星座圖更加緊密,因此有利于提高均衡器的判決性能。同時可以看到,均衡器輸出存在有相位旋轉,這主要是在信道恢復時,只保證了幅度一致性,而沒有保證相位的完全恢復,這可以通過鎖相環(PLL)或一些相位恢復算法來進行處理。

表3 Tong算法與本文算法剩余NRMSETable 3 The odd NRMSE of Tong and this paper algorithms
圖5為在復信道條件下,Tong算法與本文算法剩余NRMSE比較。可以看出,在不同的SNR條件下,本文算法較Tong算法同樣具有較小的NRMSE。
4 結語
本文提出了一種新型的基于二階統計量的相關信源盲均衡與辨識算法,通過對輸入信源的自相關矩陣的分析及推導,利用較短的觀察數據完成了系統的盲均衡與辨識。在本文的算法中:僅通過i=0,1時,根據Rs(0),Rs(1)來尋找(3)式的信道矩陣H。文獻[5]使用了Rs(a),Rs(a+1),…,Rs(a+d-1)來求其中的關鍵矩陣Q從而得到辨識信道H,與之相比本文的算法大大減小了復雜度和運算量,從理論推導過程及MATLAB仿真表明該算法是一種更一般的相關信源盲均衡與辨識算法。
[1]Liu H,Xu G,Tong L,Kailath T.Recent developments in blind channel equalization:from cyclostationarity to subspace[J].Sig.Proc,1996:1-17
[2]Tong L,Perreau S.Multichannel blind identification:from subspace to maximum likelihood methods[J].Pro.IEEE, Oct,1998:18-35
[3]Tong L,Xu G H,Kailath T.Blind identification and equalization based on second order statistics:A time-domain approach[J].IEEE Trans.Inform.Theory,1994,40(2):340-349
[4]Andrzej CHCHOCHI,Shun-AMARI.自適應盲信號與圖象處理[M].北京:電子工業出版社,2005:422-430
[5]Kaywan HAfkhmie,Zhi-Quan(Tom)Luo.Blind identification of FIR Systems Driven by Markov-Like Input Signals[J]. IEEE Transactions on Signal Processing,2000,48(6):1726-1736
[6]Simon Haykin.自適應濾波器原理[M].第四版.鄭寶玉等譯.北京:電子工業出版社,2006:108-119
[7]Chong-Yong Chi,Chih-Chun Feng,Chii-Horng Chen,et al.Blind Equalization and System Identification:batch
processing algorithms,performance applications[M].London:Springer-Verlab London Limited,2006
Blind Equalization and Identification Algorithm on Correlated Input Signal Based on Second Order Statistics
CHEN Jing
Baotou Normal Colloge of Inner Mongolia University of Science and Technology,Baotou014030,China
In this paper,we centered on the correlated input signal implementation of blind equalization algorithm based on the second-order statistics.The estimation of channel parameters could be transferred into solving feature vector by using the self-correlation matrix of the receiving signal.The emulation showed that this algorithm which used little data exhibited better equalization and identification results for the correlated input signal,and effectively decreased the effect of ISI.
Blind equalization;blind identification;over-sample;forward linear prediction error;second-order statistics
TN911.72
A
1000-2324(2014)05-0755-06
2013-03-25
2013-04-02
國家自然基金(61163025);包頭師范學院青年科學基金(BSYKJ2011-24);包頭師院教改課題(BSJG13Y034)
陳靜(1981-),女,碩士,講師.研究方向:現代信號處理,嵌入式系統及物聯網技術應用.E-mail:chenjingkeke62@163.com

