Hom-quadri-代數和Hom-octo-代數

安慧輝，薛 晨，康 健

（遼寧師范大學 數學學院，遼寧 大連 116023）

0 引言

Dendriform 代數、quadri-代數、octo-代數都稱為Loday 代數，這些代數都有共同“分裂結合性”的特性，即將結合代數的乘法表示成一串二元運算的和[1]。同時，Loday 代數在許多領域中也有廣泛的應用，甚至某些代數還成為了一個獨立的代數體系發展起來，例如1995 年Loday 在研究代數K-理論時首先發現的dendriform 代數[2]，后來隨著人們對dendriform 代數的深入研究，發現它在許多數學、物理領域中都有廣泛的應用，例如operads 理論[3]，同調[4]，Hopf 代數[5,6]，李代數和Leibniz 代數[4]，以及量子場[7]等等。本文就在octo-代數、quadri-代數基礎上分別給出Hom-quadri-代數和Hom-octo-代數的定義和結構，并討論了它們之間的關系。

1 基本內容

定義1.1(Hom-associative-代數)[8]

定義1.2(Hom-pre-Lie-代數)[8]

定義1.3(Hom-dendriform-代數)[8]

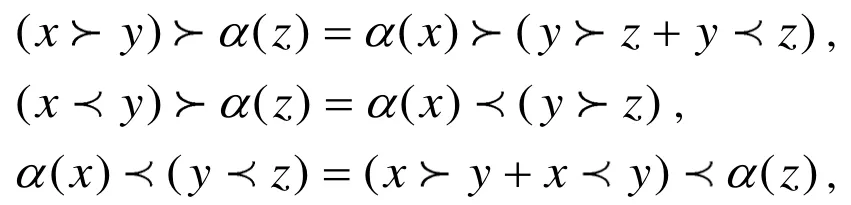
命題1.4[8]

命題1.5[8]

定義1.6(quadri-代數)[1]

假設A 為線性空間，在A 上定義代數運算

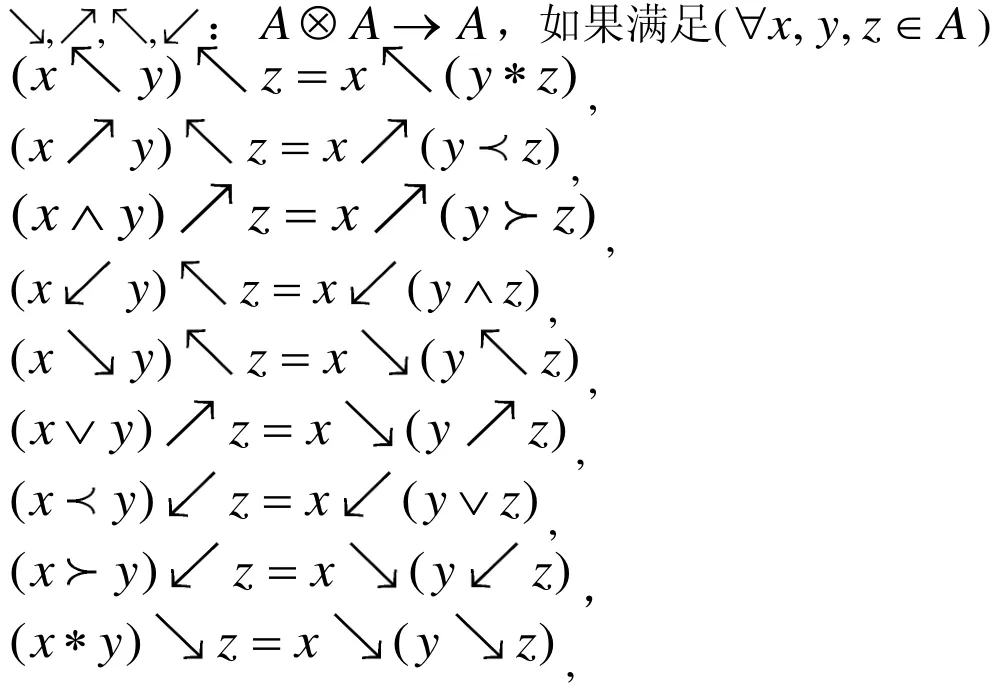
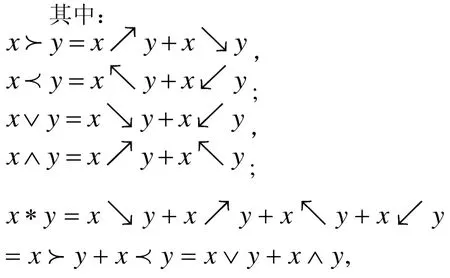
定義1.7(octo-代數) [1]

假設A 為一個線性空間，在A 上定義代數運算

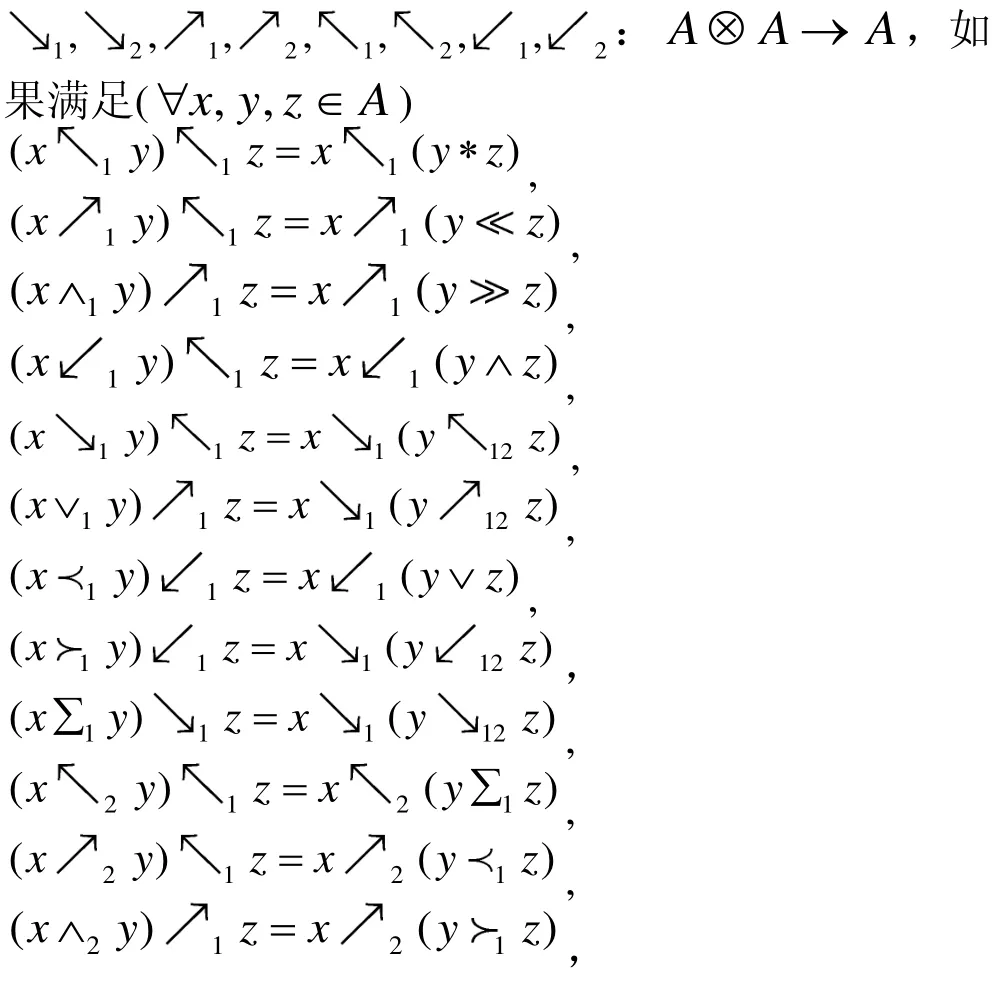
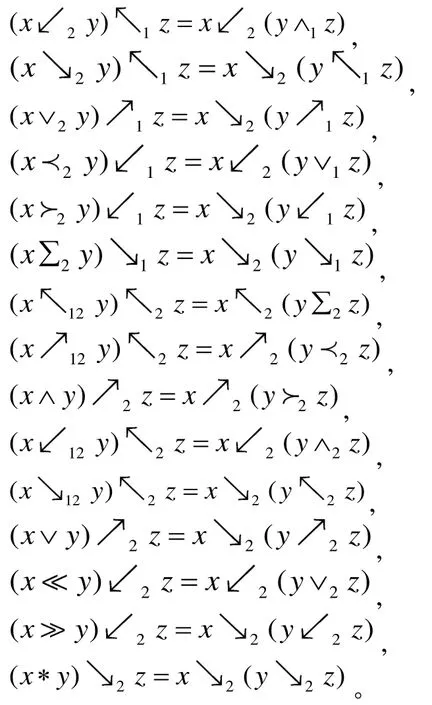
其中：

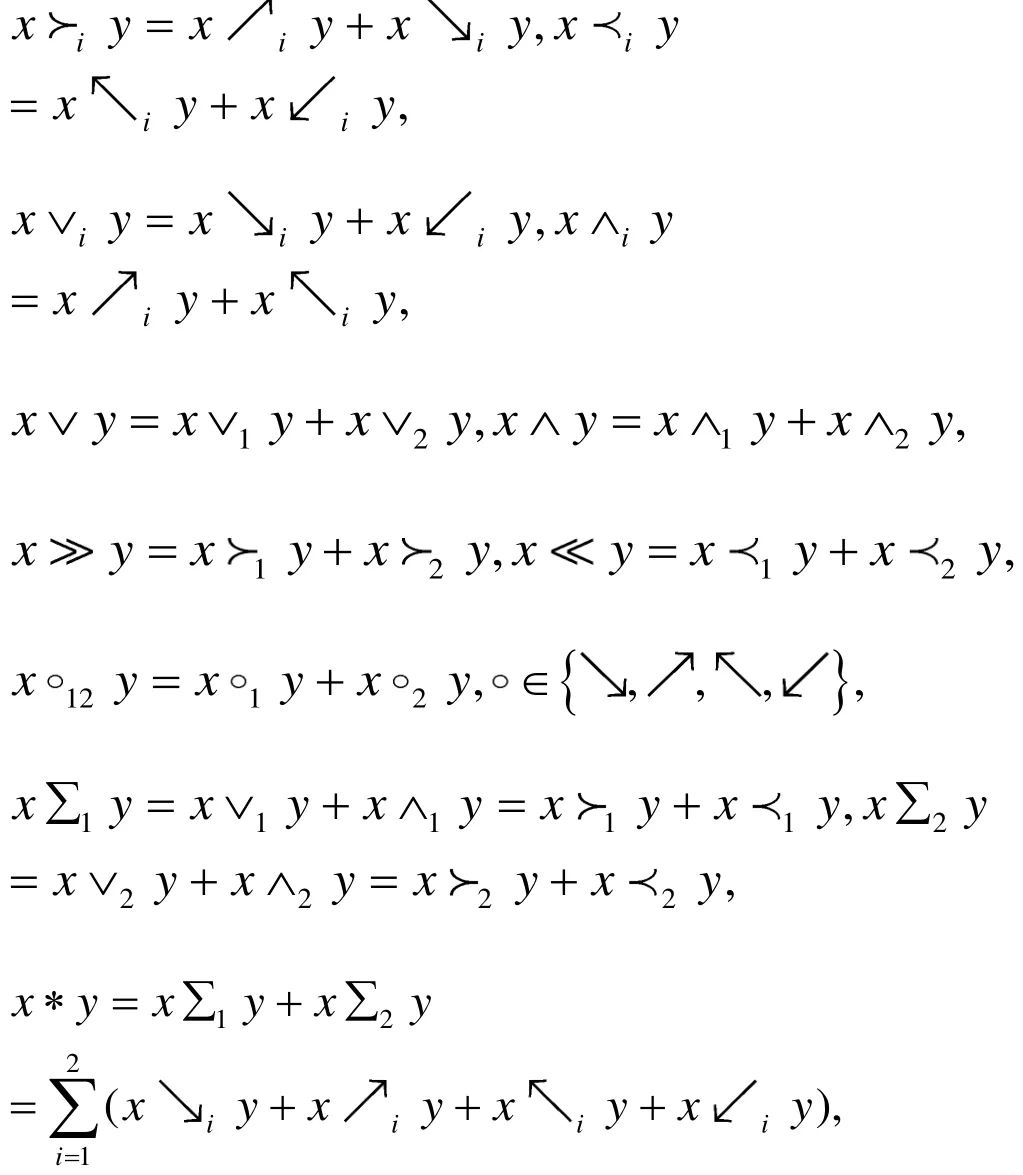
2 Hom-quadri-代數

定義2.1(Hom-quadri-代數)

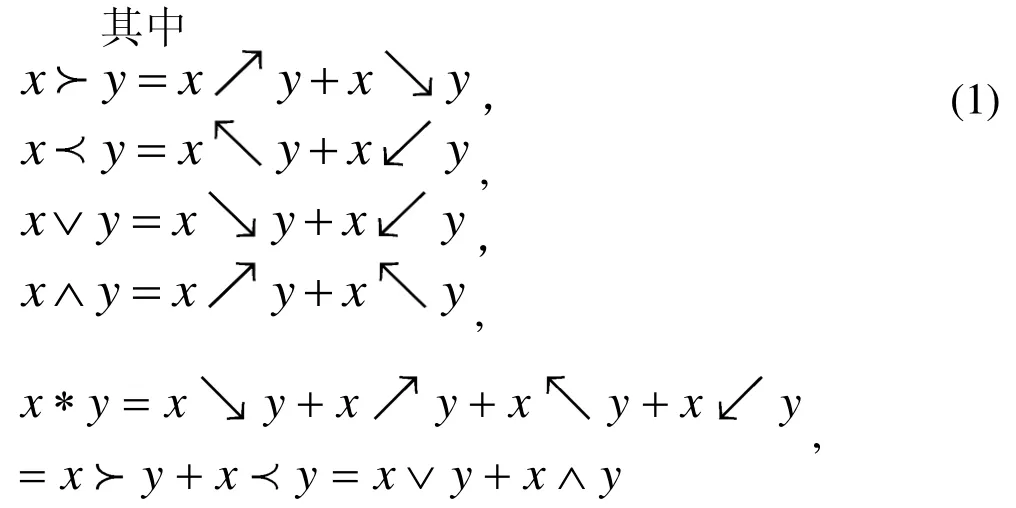
注：

定理2.2

證明：

對于 ?x , y ,z ∈ A ，有

命題2.3

證明：

對于 ?x , y ,z ∈ A ，由Hom-dendriform-代數的定義可得：

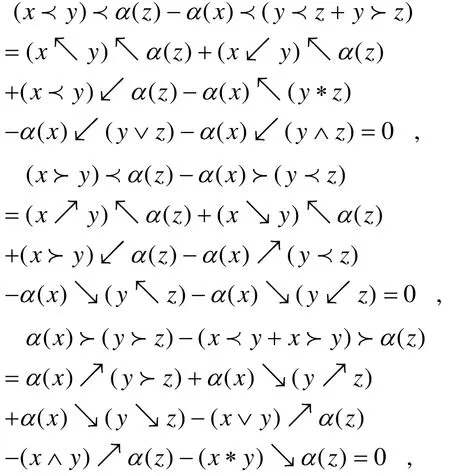
推論2.4

證明：

利用定義1.2、命題1.5 和命題2.3 即可證明。

推論2.5

證明：

利用定義1.1、命題1.4 和命題2.3 即可證明。

3 Hom-octo-代數

定義3.1(Hom-octo-代數)

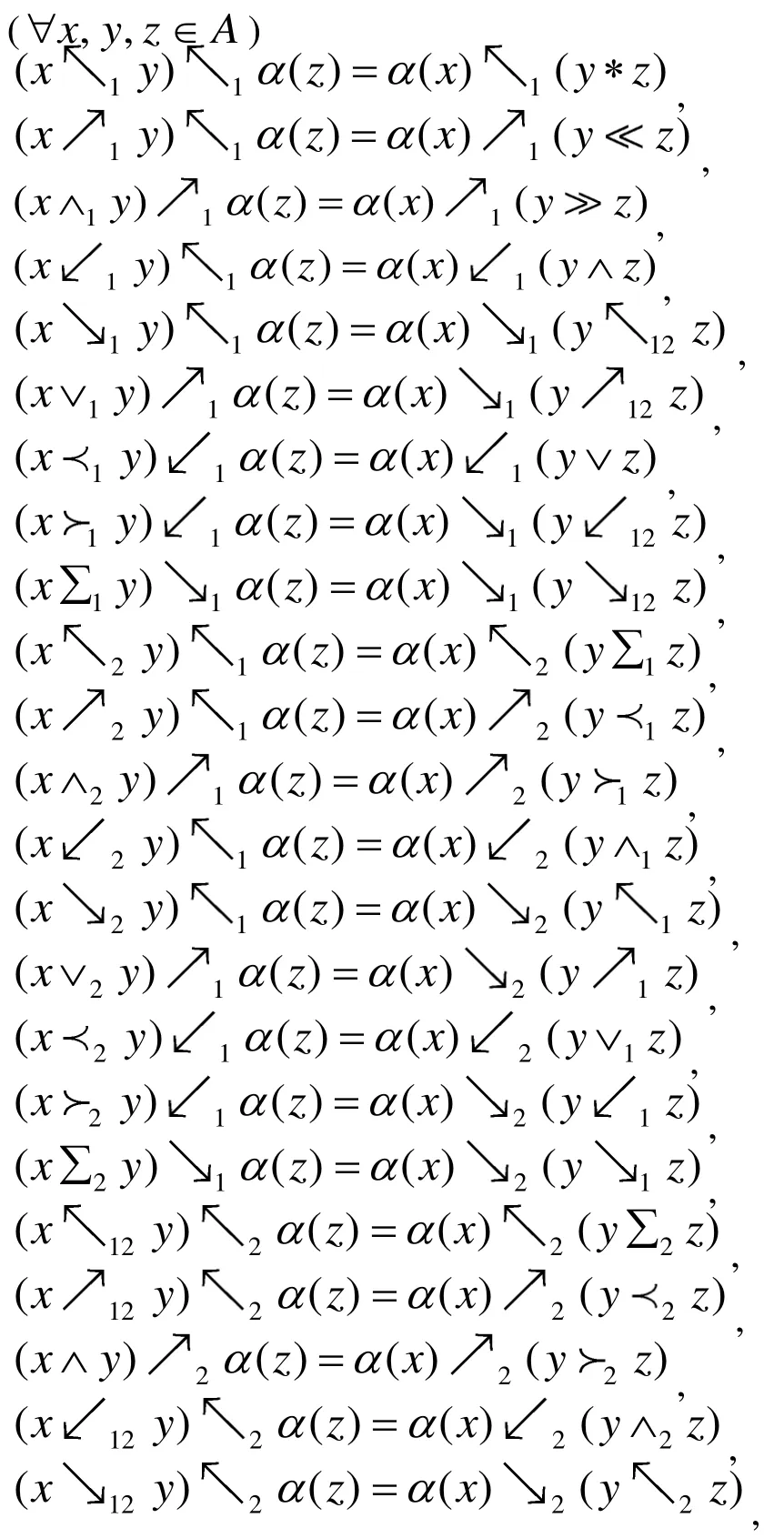
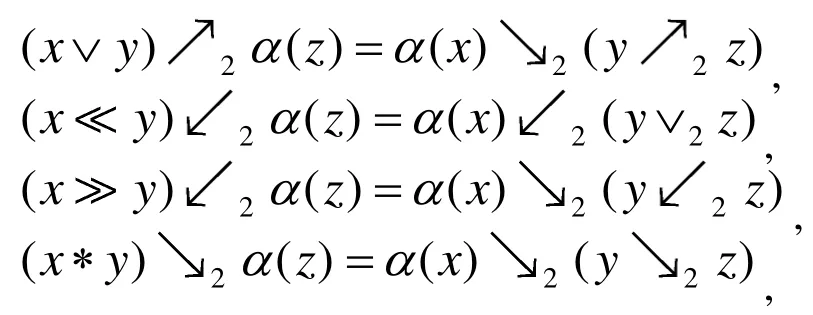
其中：

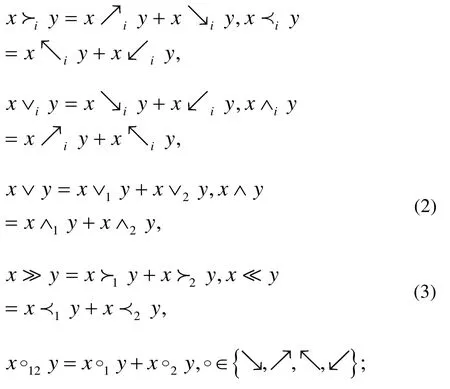
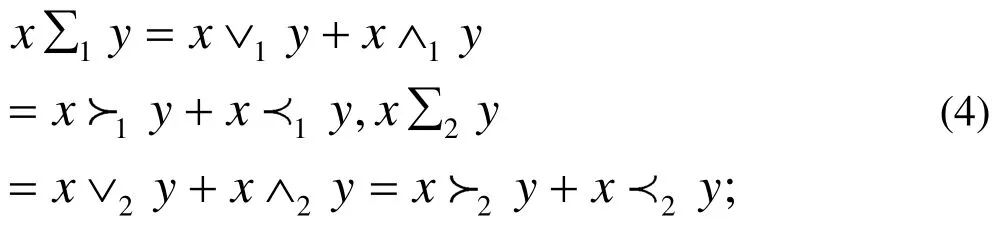
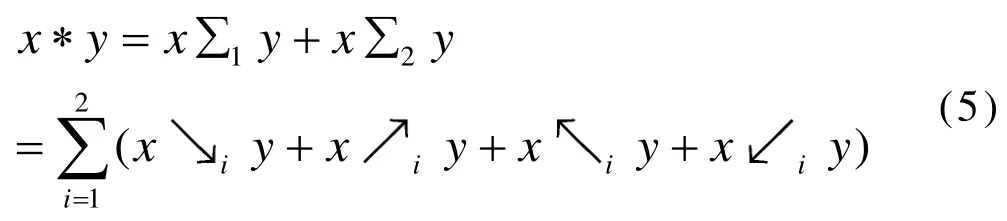
注：

定理3.2

證明：

對于 ?x , y ,z ∈ A ，有

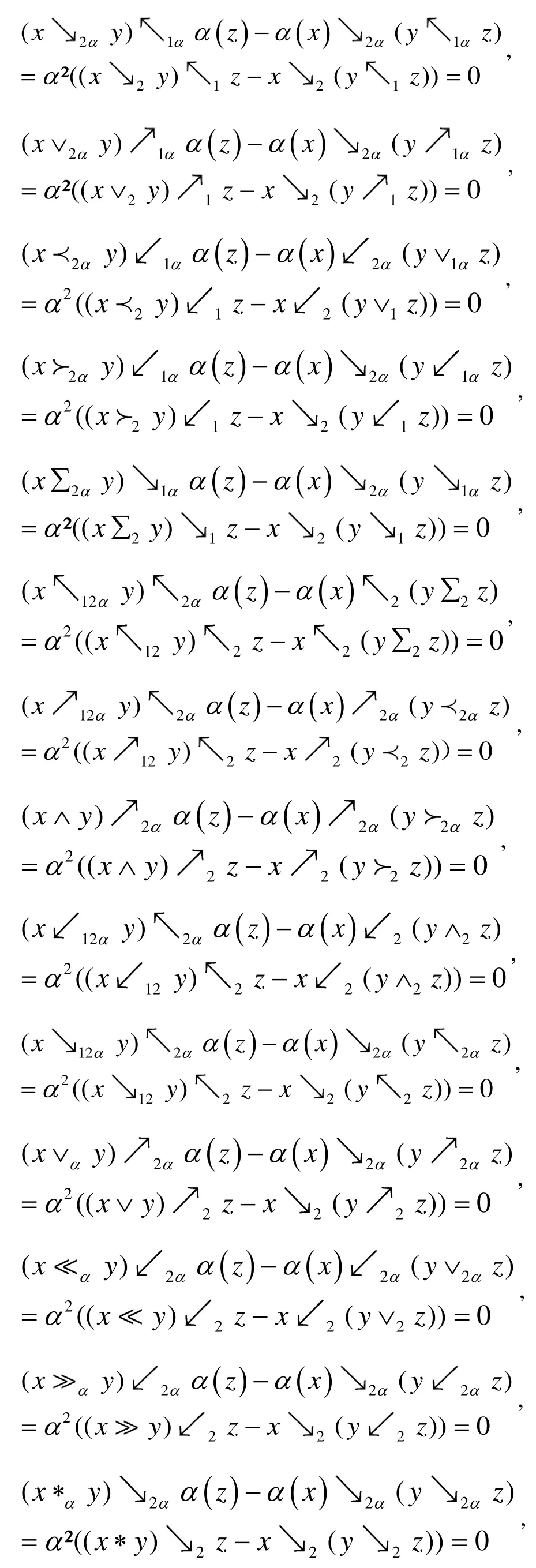
命題3.3

證明：

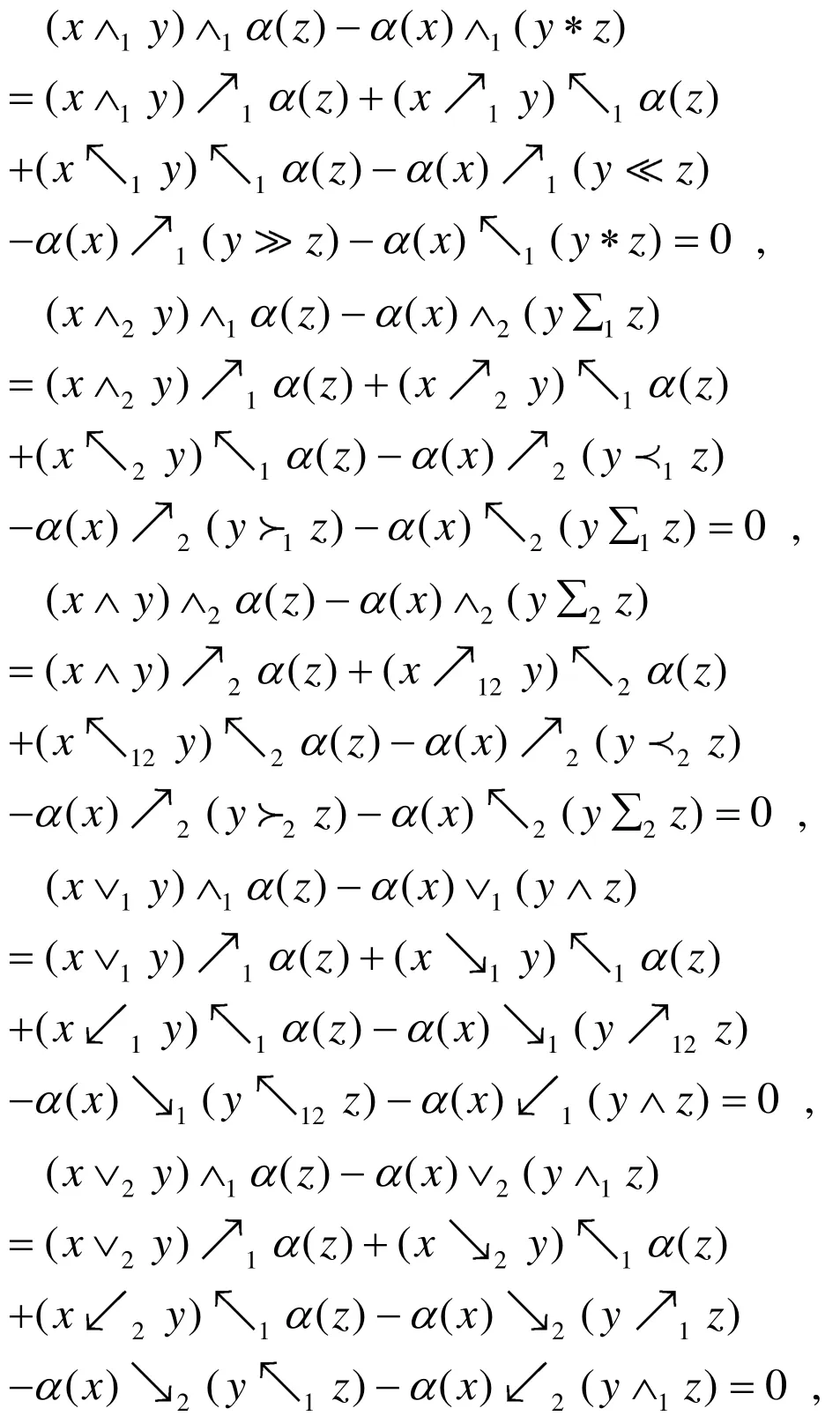
推論3.4

證明：

由定義1.3 和命題3.3 即可證明。

推論3.5

證明：

由定義1.2、命題1.5 和推論3.4 即可證明。

推論3.6

證明：

由定義1.1、命題1.4 和推論3.4 即可證明。

[1] Bai CM. O-operators of Loday algebrasand analogues of the classical Yang-Baxter equation[J]. Comm. in Alg., 2010, 38(11): 4277-4321.

[2] Loday J L, Dialgebras, in Dialgebras and related operads [J]. Lec. Not. in Math., 2001, 1763: 7-66.

[3] Loday J L, Scindement d’associativité et algèbres de Hopf [J]. Pro. of the Con. in hou. of hou. of Jean Leray, 2004, 9: 155- 172.

[4] Frabetti A, Leibniz homology of dialgebras of matrices [J]. Jour. of Pure and App.Alg., 1998, 129(2): 123-141.

[5] Ronco M, Eulerian idempotents and Milnor-Moore theorem for certain non-cocommutative Hopf algebras [J]. Jou. Alg., 2002, 254(1): 151-172.

[6] Chapoton F, Un théorème de Cartier-Milnor-Moore-Quillen pour les bigèbres dendriforms et les algebras braces [J]. Pure and App. Alg., 2002, 168(1): 1-18.

[7] Koszul J L, Variétés localement plates et convexitè [J]. Ocaka Jour. of Math., 1965, 2(2): 285-290.

[8] Makhiouf Abdenacer. Hom-dendriform algebras and Rota- Baxter Hom-algebras [J/OL]. (2011-1-2) [2014-06-10]. http:// arxiv.org/pdf/1101.0435.pdf.