存在無風險證券的投資組合選擇模型及其應用研究

隋云云，馬樹才

（1.遼寧大學 經濟學院，遼寧 沈陽 110031；2.濰坊學院 數學與信息科學學院，山東 濰坊 261061）

存在無風險證券的投資組合選擇模型及其應用研究

隋云云1,2，馬樹才1

（1.遼寧大學 經濟學院，遼寧 沈陽 110031；2.濰坊學院 數學與信息科學學院，山東 濰坊 261061）

基于可能性理論，利用可能性均值作為對證券投資組合收益的度量，以可能性方差作為證券投資組合風險的度量，建立了存在無風險證券情況下的投資組合選擇模型，最后結合實例說明該模型的實用性。

可能性均值；可能性方差；無風險證券；三角模糊數

一、引言

Harry Markowitz于1952年在其發表的論文[1]中率先提出均值-方差模型，將不確定條件下的投資組合問題模型化，此后，許多學者都是在這一理論基礎上展開投資組合理論的研究工作[2-4]。由于在Markowitz模型中需要計算所有風險證券之間的協方差，計算量比較大，為了克服這一困難，許多學者提出了一些新的組合投資模型。如：Markowitz[5]提出的以半方差作為風險函數的度量，Konno和Yamazaki提出的以絕對偏差作為風險函數的度量，以及Cai等提出的L∞風險函數。

傳統的均值-方差模型建立在概率論的基礎上，用隨機變量來描述風險資產未來收益的不確定性，但是由于金融市場的復雜性，且投資受到如投資環境、投資者年齡、性別及投資者的信息認知能力等諸多模糊因素的影響，模糊因素對投資市場的影響已逐漸受到關注。近年來，許多學者在模糊投資組合選擇方面也做出了大量的研究工作。Tanaka和Guo于2000年在文獻中將證券的收益率看作可能性變量，根據專家給出的歷史收益率的樣本與未來證券市場狀態之間的相似程度，并以此確定投資組合收益率的可能性分布，提出了可能性中心差值模型。Calsson和Fullér在文獻中給出了模糊數的上下可能性均值的概念，以及兩種可能性方差的概念；隨后Calsson和Fullér又在文獻中利用第一種可能性方差基于效用函數給出了一種證券投資組合模型及其可能性解法。

本文利用Calsson和Fullér中所定義的第一種可能性方差，建立了存在無風險證券情況下的投資組合選擇模型，并結合實例說明該模型的實用性。本文將按如下思路進行：第二部分將介紹三角模糊數的定義及性質；第三部分給出模糊數的可能性均值、可能性方差以及它們的性質；第四部分將利用可能性均值作為對證券投資收益的度量，以可能性方差作為對證券投資風險的度量，建立一種新的可能性均值-方差模型，并研究可能性分布為三角模糊數情況下的組合投資模型的形式及求解方法；第五部分將給出一個實例說明該模型的實用性。

二、預備知識

（一）相關定義

定義1[6]設是論域X到[0,1]的一個映射，即

定義 2[6]設∈ F(X)，α∈ [0,1]，令 Aα=則稱Aα為模糊集的α-截集，或稱為的α-水平集。

定義3[6]∈F(X)稱為模糊數，若

（2）?α∈(0,1]，有Aα為閉區間。

定義4[6]∈F(X)且的隸屬函數為

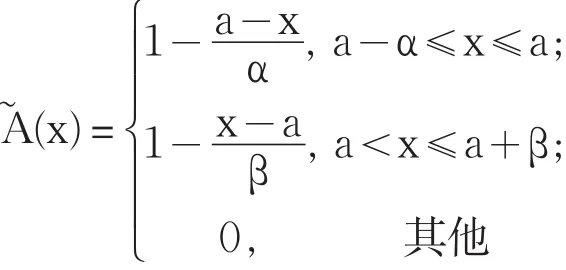
（二）有關性質

性質1[6]（線性運算性質）

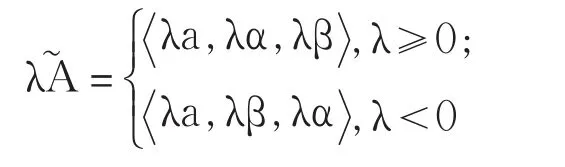
三、模糊數的可能性均值與方差的定義、性質

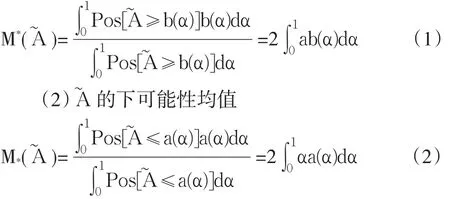
其中Pos表示可能性，具體推導過程見文獻。

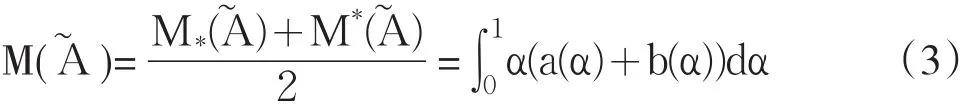
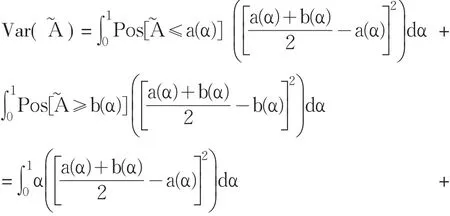
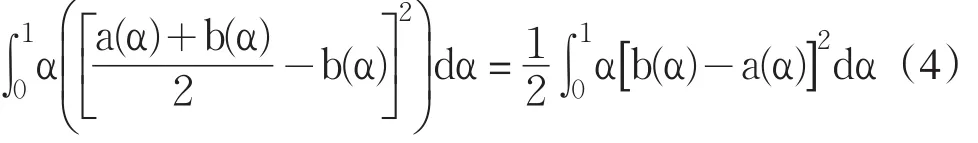
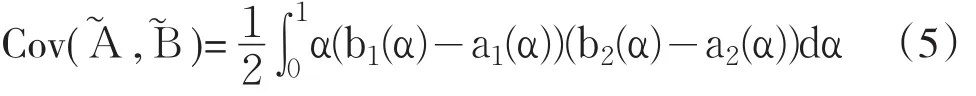
從而由定義5及定義6可知

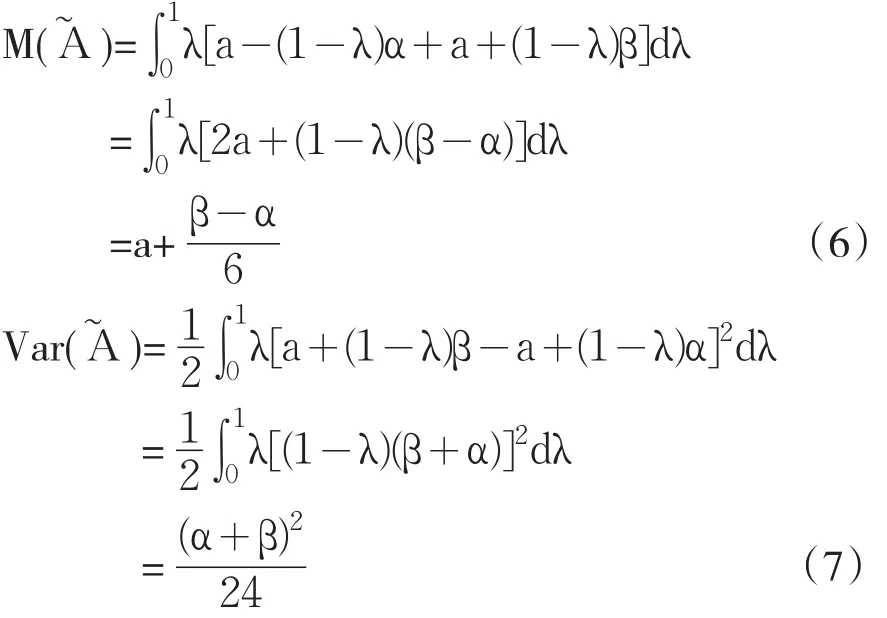
從而

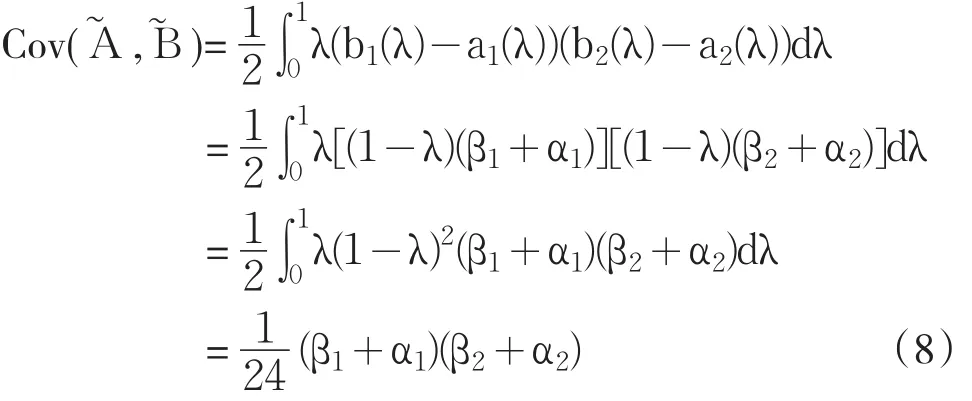
四、模型建立

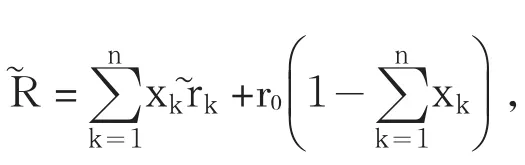
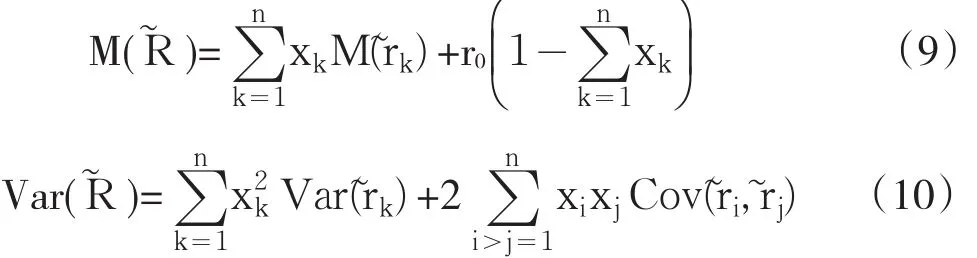
基于Markwitz的MV模型，可以建立如下的風險投資決策模型：

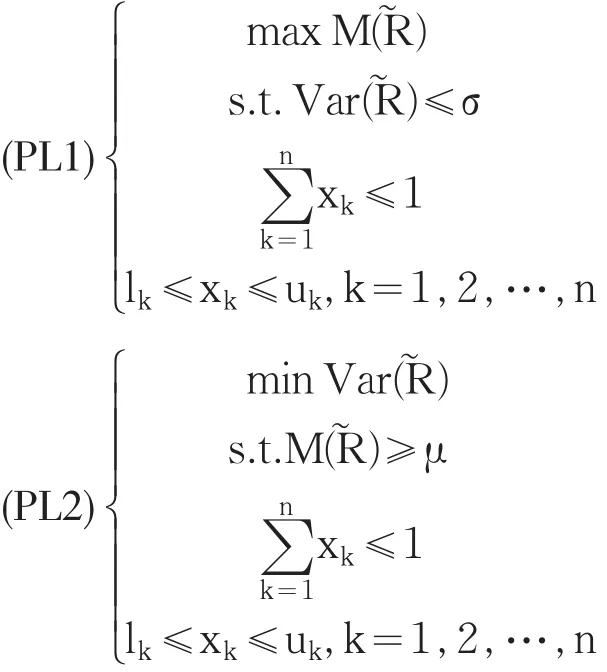
其中σ為風險上限(σ＞0)，μ為收益率的下限(μ＞0)，(PL1)，(PL2)為二次規劃模型，可以應用Matlab,Lingo等軟件編程求解。

五、實證分析

為了驗證第四部分提出的模型，本節利用從基金市場選取的工銀四季債券（代碼164808）選取的組合來進行驗證。通過RESSET金融研究數據庫可知，截至2012年12月31日，該基金擁有7種債券、1種中期票據以及銀行存款，7種債券代碼分別為110015、110016、110018、113001、113003、118007、122079。此處，我們可以將中期票據以及銀行存款一起看做是無風險投資，以5年定期存款利率作為無風險的投資利率，從而r0=5.5%。由于118007是2012年6月發行，故我們選取2012年11月到2013年10月共10多個交易日的日收益率的均值作為債券的預期收益率，其余6種債券選取從2012年6月到2013年10月共200多個交易日的日收益率的均值作為債券的預期收益率。由于債券價格同一天也是波動的，故選取三角模糊數作為債券每天的收益率，用oit、cit、lit、hit分別表示債券i在第t個交易日的開盤價、收盤價、最低價和最高價，表示債券i在第t個交易日的收益率，設其中

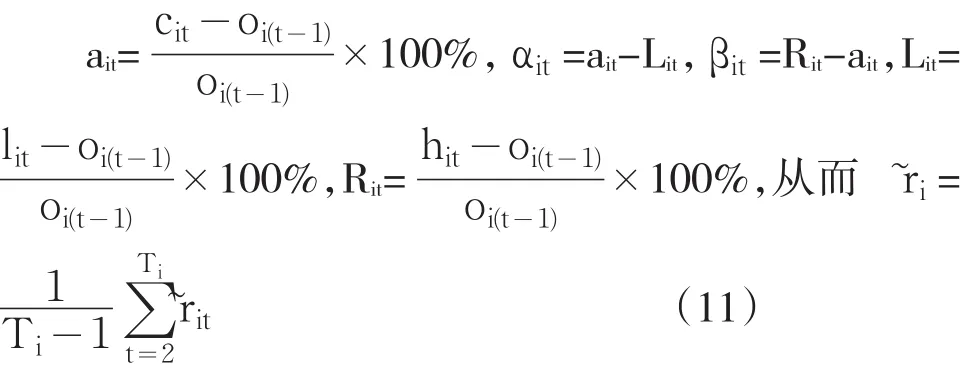
其中Ti是債券i的交易天數。

由于將收益率看作三角模糊數，故模型(PL1) (PL2)可以轉換成如下形式：

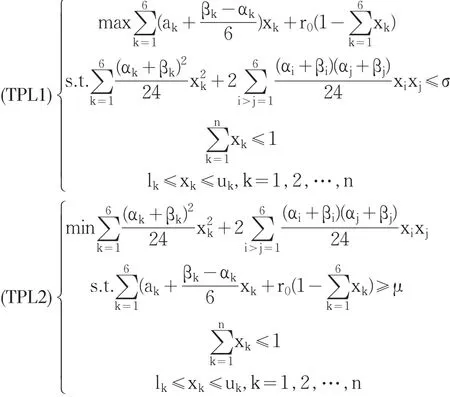
用上述方法可求得7種債券的預期收益率及可能性均值見表1。

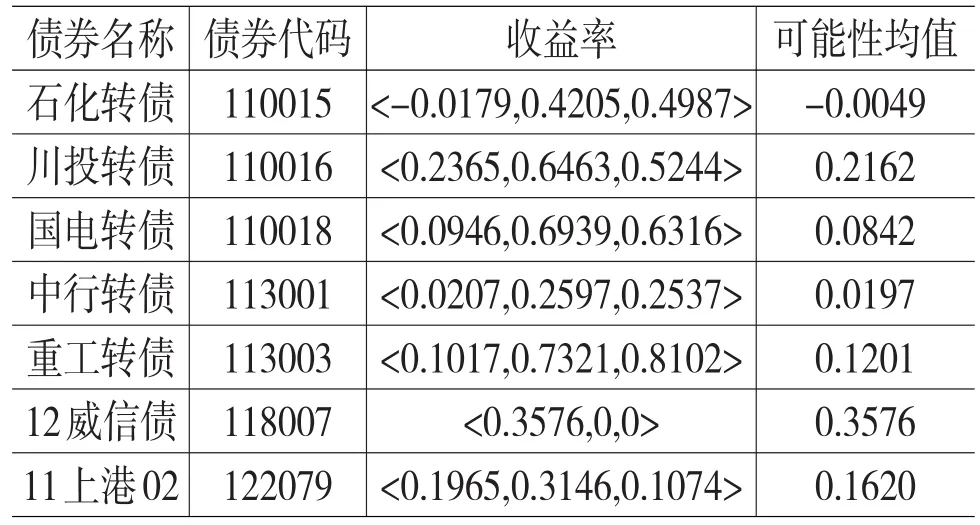
表1 7種債券的模糊收益率及可能性均值

若每種債券的投資下限分別取0.2、0.02、0.01、0.2、0.01、0.1、0.1，投資上限分別取0.3、0.03、0.02、0.4、0.02、0.2、0.2，則對于不同的σ值(TPL1)的最優解見表2。

由表2可以看出，隨著風險上限的提高收益率隨之增加，當承受的風險上限為0.007時，此時可將總資金的16.89%投入122079（11上港02），110015（石化轉債）、113001（中行轉債）、118007（12威信債）均投入總資金的20%，110016（川投轉債）投入總資金的2%，110018（國電轉債）、113003（重工轉債）均投入總資金的1%，而剩余的資金投入無風險組合。而當承受的風險上限為0.01時，此時可將總資金的25.16%投入113001（中行轉債），110015（石化轉債）、118007（12威信債）、122079（11上港02）均投入總資金的20%，3%投入110016（川投轉債），110018（國電轉債）、113003（重工轉債）均投入總資金的2%，剩余資金投入無風險組合。當承受的風險上限大于等于0.0118時，投資組合的比例不再發生變化，此時該組合能獲得的最大收益為16.25%。

表2 對應于不同風險上限的組合投資模型的投資比例及收益

若每種股票的投資下限仍取0.2、0.02、0.01、0.2、0.01、0.1、0.1，投資上限仍分別取0.3、0.03、0.02、0.4、0.02、0.2、0.2，則對于不同的μ值(TPL2)的最優解見表3。

表3 對應于不同收益下限的組合投資模型的投資比例及風險

由表3可以看出，隨著收益下限的提高風險也隨之增加，當期望收益率下限為0.1時，可將總資金的2%投入110016（川投轉債），110015（石化轉債）、113001（中行轉債）均投入總資金的20%，110018（國電轉債）、113003（重工轉債）均投入總資金的1%，118007（12威信債）、122079（11上港02）均投入總資金的10%，而剩余的資金投入無風險組合，此時承受的風險為0.6%。而當期望收益率下限為0.25時，投入這7種債券的資金比例分別23.49%、2%、1.16%、28.57%、1.23%、10.15%、13.06%，剩余資金投入無風險組合，此時承受的風險為12.06%。工銀四季債券（代碼164808）截至2012年12月31日投資的各種組合占債券組合的市值比例見表4。

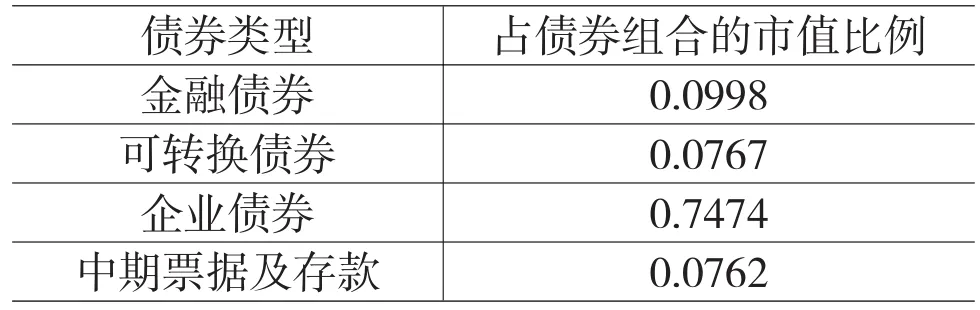
表4 164808投資的各種組合占債券組合的市值比例

通過表2、表3及表4的數據分析可以看出，該基金投資的各種債券組合的比例與表3的數據相對應，屬于風險規避型。同時也表明，第四部分建立的模型在實際的市場投資中也具有一定的指導意義。

六、結論

本文建立了一種存在無風險證券的投資組合選擇模型，但與傳統的投資組合模型不同。由于資產收益是波動的，將資產的收益率看做是模糊變量，分別將可能性均值、可能性方差看做風險資產的收益與風險的度量。根據傳統的MV模型的思想，建立了一種基于模糊變量的投資組合選擇模型，再利用模糊決策的相關理論，將模型求解問題轉化為二次規劃或線性規劃問題，從而可以使用Matlab,Lingo等軟件求解。最后通過實證分析來表明該模型對實際市場的投資具有一定的指導意義，不同風險偏好的投資者可以根據自己的風險偏好以及能夠承擔的風險和期望的收益來進行選擇投資。

[1]Markowitz H.Portfolio Selection[J].Journal of Finace,1952,（7）:77-91.

[2]Sharp,WF.Portfolio Theory and Capital Markets [J].Journalof Finace,1972,27（4）:968-969.

[3]Robert CMerton An Analytic Derivation of the Efficient Portfolio Frontier[J].The Journal of Financial and Quantitative Analysis，1972,7（4）：1851-1872.

[4]Pang,Jong-Shi.A New and Efficient Algorithm for a Class of Portfolio Selection Problems[J].OperationsResearch.1980,28（3）:754-767.

[5]Markowitz H.Portfolio Selection:Efficient Diversification of Investments[M].New York:Wiley.

[6]李洪興，汪培莊.模糊數學[M].北京：國防工業出版社，1994.

（責任編輯：張艷峰）

1003-4625（2014）08-0001-04

F830.91

A

2014-06-04

本文為國家社科基金青年項目(編號13CRK027)，濰坊市科技發展資助項目（201201112）。

隋云云（1981-），女，山東龍口人，遼寧大學經濟學院博士研究生，講師，研究方向：經濟統計，模糊數學，組合投資理論與計量經濟模型；馬樹才（1945-），男，遼寧岫巖人，教授，博導，研究方向：計量經濟模型及方法。